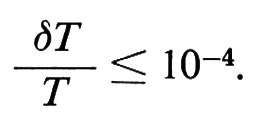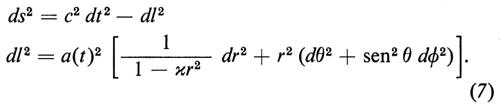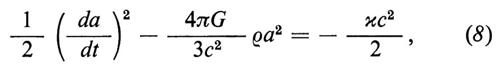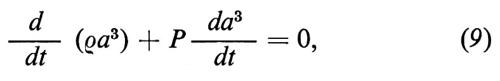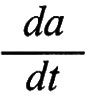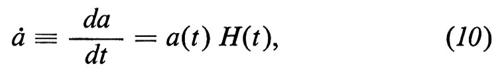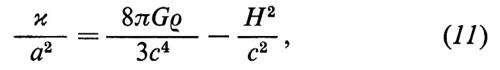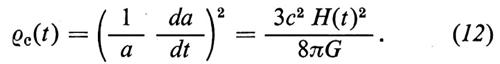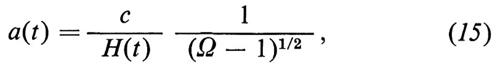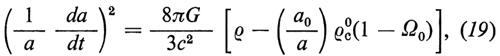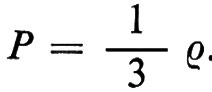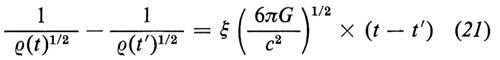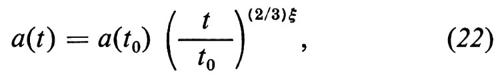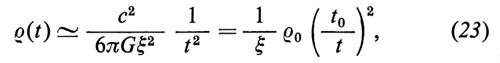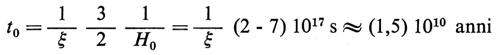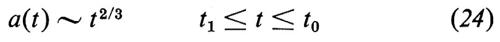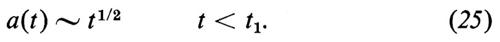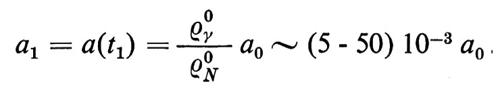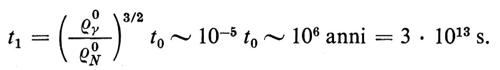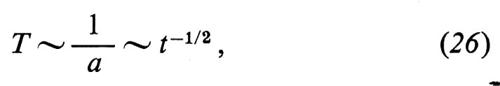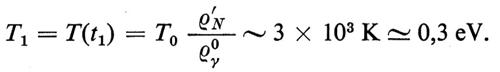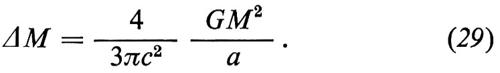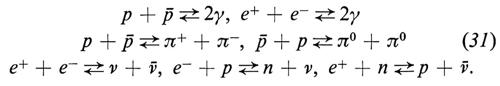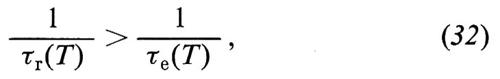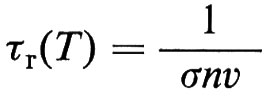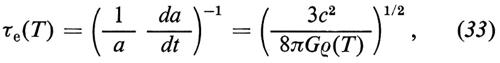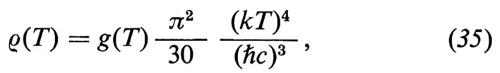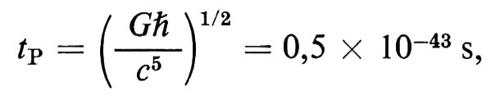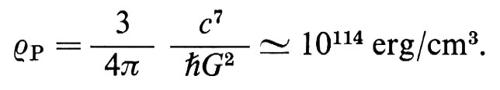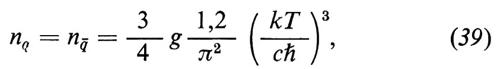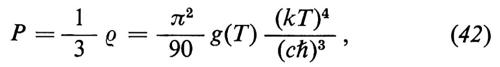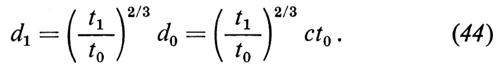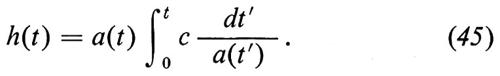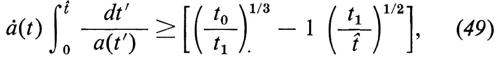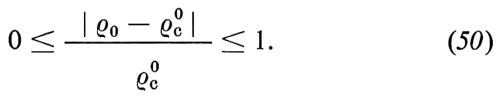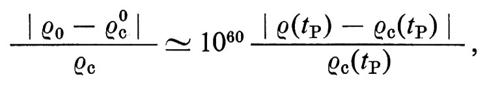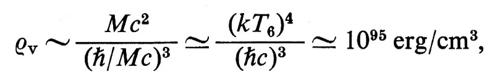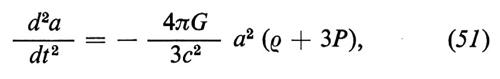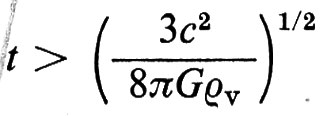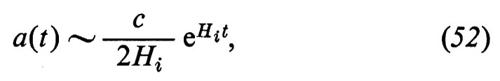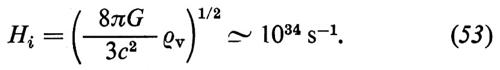Universo

Universo

SOMMARIO: 1. Introduzione.  2. La composizione attuale dell'universo: a) la distribuzione delle galassie; b) composizione chimica, densità e temperatura della materia dell'universo; c) la radiazione di fondo a microonde; d) altri componenti dell'universo; e) la massa oscura.  3. La dinamica attuale dell'universo: a) la legge di Hubble; b) l'espansione dell'universo; c) l'espansione dell'universo e l'isotropia della MBR.  4. Relatività generale e cosmologia: a) il modello cosmologico di Friedmann; b) la legge di Hubble e la densità critica; c) soluzioni dell'equazione di Friedmann; d) l'energia dell'universo nel caso x = 1. □ 5. L'evoluzione dell'universo nell'epoca radiativa (10^-5 ≤ t ≤ 10¹³s): a) la composizione del plasma; b) la scomparsa degli antinucleoni; c) il congelamento delle interazioni deboli; d) la formazione dell'He⁴; e) le ultime fasi dell'evoluzione dell'universo.  6. La fisica delle prime fasi dell'esistenza dell'universo: a) la comparsa dei quarks liberi; b) l'unificazione delle interazioni fondamentali; c) l'instabilità del protone e l'asimmetria barionica dell'universo.  7. L'espansione esponenziale: a) il problema dell'orizzonte; b) il problema della curvatura; c) l'espansione esponenziale.  8. L'origine delle strutture dell'universo: a) la gravitazione come causa delle strutture; b) impossibilità della formazione delle strutture dal gas neutro di idrogeno ed elio; c) la materia oscura come origine delle strutture; d) il ruolo delle esplosioni stellari.  9. Conclusioni. □ Bibliografia.

1. Introduzione

L'illusione di poter dare una descrizione razionale dell'universo e della sua origine sembra essere una caratteristica costante del pensiero umano. Sebbene ogni epoca abbia guardato con sufficienza alle cosmologie e cosmogonie elaborate dalle epoche precedenti, mettendone in luce le ingiustificate generalizzazioni, la speranza che le conoscenze del momento fossero in grado di fornire una descrizione dell'intero universo non è mai tramontata. Il nostro secolo non fa eccezione e anzi la cosmologia gode oggi fra fisici e astronomi di una rinnovata popolarità. Anche se certo non definitiva, e sicuramente incompleta, l'immagine dell'universo che il nostro secolo al suo tramonto propone agli scienziati futuri è radicalmente diversa da quella elaborata nei due secoli precedenti. Anziché statico, eterno e infinito, come era concepito alla fine dell'Ottocento, l'universo ci appare oggi come una struttura in evoluzione, che ha avuto inizio, che forse è chiusa, e che può avere fine. Un ritorno a concezioni precedenti? Forse, ma in una forma più elaborata e quantitativa, anche se certamente solo approssimata.

La causa prima di un mutamento così profondo è stato l'immenso arricchimento delle conoscenze empiriche dovuto al perfezionamento dei mezzi osservativi: non soltanto sono stati scoperti oggetti totalmente ignoti agli astronomi del secolo scorso - nane bianche, stelle neutroniche, sorgenti X, galassie, ammassi di galassie, quasar, ecc. -, ma è stato possibile ampliare enormemente i confini dell'universo osservabile. Si è così scoperto che, nonostante la grande varietà di strutture, l'universo è, in media, omogeneo e isotropo, descrivibile perciò, in prima approssimazione, come un gas le cui ‛molecole' sono le galassie, piccole rispetto alle distanze che le separano. Un gas, però, la cui densità decresce al passare del tempo, per l'allontanarsi di ogni ‛molecola' dalle sue vicine: questo è il significato della scoperta, fatta da E. Hubble nel 1927, che tutte le galassie si allontanano dalla nostra con una velocità di recessione proporzionale alla loro distanza. Questa scoperta ha segnato la fine dell'immagine statica dell'universo e ha aperto la strada all'attuale concezione evoluzionistica, che oggi sappiamo si applica non solo all'universo nel suo insieme, ma anche ai singoli oggetti di cui esso è composto, a cominciare dalle stelle, strutture dinamiche che nascono, si evolvono e infine muoiono.

Questa concezione dinamica dell'universo sarebbe stata probabilmente accettata con maggiore difficoltà, se non si fosse trovata in accordo almeno qualitativo con un modello di universo omogeneo, proposto qualche anno prima da A. Friedmann e ripreso poco dopo da G. Lemaître, basato sulla teoria della relatività generale. Tale teoria, formulata da Einstein nel 1916, è allo stesso tempo una teoria della gravitazione e della struttura geometrica dello spazio-tempo in presenza di materia. Le sue conseguenze verificabili in laboratorio - in verità non troppo numerose - sono state tutte confermate sperimentalmente: per questa ragione e per la sua intrinseca coerenza, la relatività generale é oggi generalmente considerata come la base teorica appropriata per una descrizione globale dell'universo e della sua storia.

La relatività generale conduce in maniera del tutto naturale a concepire l'universo come un sistema dinamico, la cui evoluzione ha avuto inizio a un istante t = O - che, come vedremo, possiamo situare intorno a 10-20 miliardi di anni fa - e il cui moto di espansione è regolato da un sistema di equazioni che legano il raggio di curvatura dell'universo, la pressione, la densità di energia, e le derivate di tali grandezze. Poiché la dinamica del sistema è deterministica, è nello stato dell'universo primordiale che dobbiamo ricercare la causa della sua situazione attuale, caratterizzata: a) da una straordinaria omogeneità su grande scala; b) da una ricca varietà di strutture su piccola scala (ammassi di galassie, galassie, stelle); c) da una densità di energia prossima a quella critica, cioè a quella occorrente perché l'universo sia chiuso, pur essendo localmente euclideo; d) da una ben determinata composizione chimica.

Per ricostruire, in questo senso, la storia dell'universo, alle equazioni cosmologiche di Friedmann, che riflettono l'effetto della gravitazione, occorre unire la cosiddetta equazione di stato, cioè la relazione fra la densità di energia e la pressione, la quale dipende essenzialmente dalle altre interazioni fondamentali, ossia dalle interazioni elettroma gnetiche, deboli e forti. Gli effetti e l'importanza relativa di tali interazioni variano al variare della densità di energia e della temperatura, che dai valori elevatissimi che avevano all'inizio dell'universo vanno progressivamente diminuendo a causa dell'espansione. La diminuzione della temperatura è dovuta al fatto che, per effetto dell'espansione, la materia dell'universo produce lavoro a entropia costante e di conseguenza la sua densità di energia e quindi la sua temperatura diminuiscono. Questo effetto è analogo al raffreddamento del gas nella fase di espansione in un motore a combustione interna. Tuttavia, contrariamente a quanto avviene in un motore, nel caso dell'universo non c'è alcuna perdita di energia dovuta alla conduzione di calore, poiché in un universo uniforme la temperatura è dovunque la stessa.

È stata una delle conquiste più significative della scienza negli ultimi trent'anni l'aver dimostrato come la conoscenza delle proprietà delle interazioni fondamentali, acquisita per mezzo di esperienze compiute in laboratorio e di una profonda elaborazione teorica, permetta di dare una descrizione soddisfacente delle varie fasi attraverso cui la materia dell'universo è passata nel corso della sua evoluzione.

Sviluppando un modello proposto da G. Gamow (v., 1948), è stato così possibile pervenire a una spiegazione qualitativa della formazione dei vari elementi che si trovano oggi nell'universo e che certamente non potevano essere presenti nelle primissime fasi della sua evoluzione. In particolare è stato possibile prevedere il valore del rapporto fra l'abbondanza attuale dell'idrogeno e quella dell'elio, valore che è risultato in buon accordo con quello osservato. Forse ancora più significativa è stata la predizione, anch'essa dovuta a Gamow (v., 1946), dell'esistenza di una radiazione elettromagnetica, con distribuzione spettrale di corpo nero, alla temperatura di pochi gradi Kelvin, diffusa uniformemente in tutto l'universo. La rivelazione di tale radiazione, dovuta ad A. A. Penzias e R. W. Wilson (v., 1965), rappresenta forse la migliore conferma della validità del modello evolutivo dell'universo, in quanto la radiazione osservata rappresenta una sorta di relitto fossile della radiazione a ben più alta temperatura presente nei primi secondi di vita dell'universo.

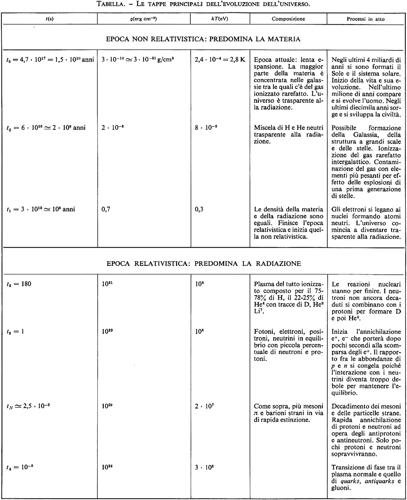
Utilizzando tutte le conoscenze oggi disponibili sul comportamento della materia in condizioni simili a quelle riproducibili con esperienze in laboratorio, possiamo seguire a ritroso l'evoluzione dell'universo dal tempo presente (t ≃ 15 miliardi di anni) fino a circa 10 μs dopo l'inizio. Questo immenso intervallo di tempo è quello che potremmo chiamare l'epoca storica, riassunta schematicamente nella tabella. A dire il vero alcuni degli avvenimenti che molto probabilmente hanno avuto luogo durante questa epoca sono ancora solo parzialmente compresi. In particolare la teoria della formazione delle strutture dell'universo - galassie, ammassi di galassie, ecc. - presenta ancora molti punti oscuri: per chiarirli occorre avere dati astronomici più sicuri sull'entità della massa oscura presente nelle galassie e negli ammassi di galassie, e conoscenze più precise sulle proprietà di alcune particelle elementari - in particolare sulla massa del neutrino - o sull'esistenza di nuove particelle, postulate dalle più recenti teorie.

Del resto queste conoscenze sono certo indispensabili per ricostruire l'evoluzione dell'universo nei primi 10 μs della sua esistenza, in quel brevissimo periodo cioè che potremmo chiamare la preistoria dell'universo. La divisione fra storia e preistoria è stata posta al tempo t = 10 μs perchè alla temperatura corrispondente a tale data, T ~ 2 • 10¹² K, si ha ragione di ritenere che lo stato della materia cambi bruscamente con una transizione di fase simile a quella che fa passare l'acqua dallo stato gassoso a quello liquido. In questo caso la transizione di fase dovrebbe consistere nella rapida sparizione dei quarks e dei gluoni liberi, presenti nella fase iniziale dell'universo, e nella formazione di particelle adroniche normali, cioè protoni, neutroni, mesoni π, ecc. (v. particelle elementari: Struttura delle particelle). Si noti che la presenza dei quarks all'interno degli adroni può considerarsi ormai un fatto ben stabilito, mentre ancora non sono stati osservati quarks liberi. È probabile che fra non molto la transizione di fase che porta alla liberazione dei quarks possa essere studiata in laboratorio con esperienze di urti fra ioni pesanti relativistici.

Man mano che ci avviciniamo all'istante iniziale, le condizioni fisiche della materia si allontanano sempre più da quelle accessibili all'esperienza, e tutto lascia supporre che non si potranno mai riprodurre in laboratorio le enormi densità di energia e le temperature che esistevano all'inizio dell'universo. L'unica guida per ricostruire l'evoluzione dell'universo nel periodo preistorico resta oggi la teoria delle interazioni fondamentali, che i fisici stanno attivamente sviluppando in questi anni. Tale teoria prevede che alle altissime energie, che necessariamente esistevano nell'universo 10^-34 − 10^-36 secondi dopo l'istante iniziale, le interazioni elettromagnetiche, deboli e forti, divengano ugualmente intense e anzi essenzialmente indistinguibili, mentre compaiono nuove forme di materia ancora mai osservate sperimentalmente. È del tutto concepibile che, mentre le conoscenze fisiche acquisite dalle esperienze di laboratorio hanno permesso di ricostruire l'evoluzione dell'universo in quello che abbiamo chiamato il periodo storico, la situazione si inverta per il periodo preistorico. È possibile infatti che i residui fossili di tale periodo, se esistono e se i loro effetti potranno in avvenire essere rivelati, forniscano l'unica possibile conferma delle teorie che i fisici stanno elaborando in questi anni.

La speranza che lo studio del macrocosmo possa portare alla conoscenza delle leggi che governano il microcosmo è probabilmente la ragione più importante del favore di cui oggi gode la cosmologia. Questa impone alle teorie che i fisici vanno elaborando di soddisfare a vincoli che, per quanto in apparenza assai generali, sono in realtà piuttosto restrittivi. Invero dallo stato iniziale, verosimilmente assai uniforme e governato da leggi dotate di altissima simmetria, deve essersi potuto evolvere un universo isotropo, seppure strutturato, nel quale la materia prevale sull'antimateria, la densità numerica dei fotoni è un miliardo di volte maggiore di quella dei protoni, mentre la densità di energia è dell'ordine di quella critica. Ad alcune di queste condizioni le teorie più recenti sembrano poter soddisfare, ma la mancanza di dati osservativi sicuri sulla massa oscura dell'universo, sul valore esatto della costante di Hubble, sulla massa di alcune particelle elementari e sull'esistenza di altre impedisce di stabilire condizioni certe.

Non tutti gli argomenti che abbiamo qui brevemente riassunto verranno sviluppati nel seguito di questo articolo. In particolare non discuteremo il problema della formazione degli elementi pesanti, per il quale rimandiamo all'articolo origine degli elementi; neppure tenteremo di riassumere la teoria delle interazioni elementari, per la quale il lettore potrà consultare gli articoli particelle elementari e, per gli aspetti più recenti, teorie unificate.

Nel cap. 2 esporremo brevemente la composizione attuale dell'universo e nel cap. 3 riassumeremo i dati essenziali sulla sua dinamica. Informazioni più dettagliate sul contenuto di questi due capitoli si trovano negli articoli astronomia e astrofisica, sistemi stellari, quasar, materia e radiazione interstellare.

Nel cap. 4 riassumeremo il modello di Friedmann, rinviando il lettore, per un'esposizione più completa della teoria della relatività generale, ai due articoli Relatività e Gravitazione e cosmologia (v. relatività), mentre per le sue conseguenze cosmologiche rinviamo all'articolo cosmologia.

Il cap. 5, che tratta dell'evoluzione dell'universo durante la prima parte di quello che abbiamo chiamato il periodo storico (10^-5 s ≤ t ≤ 10⁶ anni), contiene i risultati più attendibili della moderna cosmologia. Nel cap. 6 discuteremo brevemente le trasformazioni attraverso cui è passata, secondo le attuali teorie, la materia dell'universo nel periodo anteriore a 10^-5 s. Nel cap. 7 esporremo le basi di un modello recentemente proposto (modello inflazionistico), che permette di eliminare alcune incongruenze del modello cosmologico usuale. Il cap. 8 contiene una breve esposizione delle teorie attuali sulla formazione delle strutture osservate oggi nell'universo. Infine nell'ultimo capitolo riassumeremo i più importanti risultati e accenneremo ai possibili sviluppi futuri.

2. La composizione attuale dell'universo

a) La distribuzione delle galassie.

Il Sole con il suo sistema planetario è una stella che assieme a circa cento miliardi di altre stelle forma la nostra galassia: la maggior parte di queste stelle è concentrata all'interno di una regione a forma di lente più o meno piatta con uno spessore dell'ordine di 200 pc e con un diametro di 20.000 pc (1 pc ≃ 3 • 10¹⁶ m; 1 Mpc = 10⁶ pc). Al di fuori di tale lente, la densità di stelle decresce rapidamente. Oltre alla nostra, ci sono molte altre galassie, alcune più piccole, altre più grandi. La densità media di galassie è dell'ordine di 0,01 per Mpc³, il che corrisponde a una distanza media tra galassie vicine di circa 4 Mpc.

Le galassie sono distribuite in maniera non uniforme nello spazio. Ci sono alcuni ammassi giganti con 10.000 galassie in una sfera del diametro dell'ordine di 5 Mpc: la densità di galassie in tali ammassi è circa mille volte superiore a quella media.

Una misura quantitativa della non uniformità della distribuzione delle galassie si ottiene studiando le correlazioni fra le loro distanze. Si è osservato che la probabilità di trovare una galassia a una piccola distanza da un'altra (scelta a caso) è superiore alla probabilità media di trovare una galassia in una sfera di raggio uguale a tale distanza. La probabilità di correlazione è doppia della probabilità media a una distanza caratteristica dell'ordine di 5 Mpc: recentemente si è scoperto che anche per gli ammassi di galassie esiste una distanza caratteristica, di circa 50 Mpc, alla quale la probabilità di trovare un altro ammasso è doppia della probabilità media.

Su una distanza dell'ordine di 1.000 o 2.000 Mpc, invece, non è stata finora osservata alcuna correlazione: su tale scala l'universo può considerarsi con buona approssimazione uniforme. Ciò significa che ogni cella dii .000 Mpc di lato contiene la stessa massa indipendentemente dalla posizione della cella. Sotto questo aspetto possiamo paragonare l'universo a un gas, nel quale le singole galassie rappresentano le molecole, la cui distanza reciproca è superiore alla dimensione delle molecole stesse. Mentre il numero di molecole contenute in un volume molto piccolo può variare a caso da O a 1 o 2 e così via, le variazioni del numero di molecole in un volume grande sono relativamente piccole. Si può perciò usare una trattazione cinetica considerando l'insieme delle galassie come un fluido con una data densità, come si fa nella teoria cinetica dei gas. Vi è però una differenza notevole tra le galassie e le molecole dei gas normali: mentre le forze tra le molecole hanno un corto raggio d'azione, l'attrazione gravitazionale tra galassie diminuisce assai lentamente con l'aumentare della distanza.

La maggior parte degli studi effettuati prima della metà degli anni settanta è stata fatta usando immagini fotografiche che mostravano la posizione delle galassie proiettate sulla sfera celeste. Da allora si sono misurate le distanze che ci separano da più di 10.000 galassie (illustreremo più avanti il metodo usato per tali misure): si è così ottenuta un'immagine tridimensionale della distribuzione delle galassie nel volume preso in esame, e si è scoperto che esiste una struttura caratteristica su larga scala. Sono stati identificati vari superammassi (superclusters) di galassie, che formano superfici e linee lungo le quali si concentrano le galassie stesse: le dimensioni caratteristiche di tali superammassi sono dell'ordine di 100 o 200 Mpc. Tra un ammasso e l'altro si sono scoperte delle ‛regioni scure' spesso dette ‛vuoti' (voids) del volume di 100 Mpc³, dove non esiste alcuna galassia; naturalmente, però, tali ricerche mostrano soltanto che non ci sono galassie con una luminosità superiore a un certo limite, che è generalmente pari al 10% circa di quella della nostra galassia, e per ora non è chiaro se nella regione scura esistano o meno delle galassie meno luminose. Nonostante questi recenti risultati occorre tener presente che la struttura dell'universo su grande scala è ancora in gran parte sconosciuta.

b) Composizione chimica, densità e temperatura della materia dell'universo.

Le galassie sono formate per il 90% da stelle più o meno simili al Sole, ma la maggior parte della luce proviene da una minoranza di stelle giovani, luminosissime ed estremamente massicce (da dieci a cento volte più pesanti del Sole). Si noti che, mentre gli strati esterni del Sole sono composti per circa il 73% da idrogeno, per il 25% da elio e per il 20% da elementi più pesanti, le stelle che riteniamo più vecchie del Sole contengono una quantità molto minore di elementi pesanti.

Le galassie contengono, oltre alle stelle, del gas interstellare, la cui temperatura varia moltissimo: da 30-100 K, nelle nubi fredde (in cui una gran parte degli atomi sono legati in molecole tipo H₂0, CO, CH₂O, o in molecole più grandi ancora), a parecchie migliaia di gradi, nel gas più caldo e fortemente ionizzato dalle onde d'urto delle esplosioni stellari. La massa totale del gas rappresenta soltanto una piccola frazione - normalmente inferiore al 10% - della massa di una galassia. È importante notare che una parte rilevante del gas non proviene da esplosioni stellari e perciò la sua composizione è prossima a quella iniziale, non inquinata cioè dai prodotti delle reazioni nucleari che avvengono all'interno delle stelle.

Gli ammassi di galassie contengono un plasma estremamente caldo - gas interamente ionizzato - la cui temperatura è dell'ordine di qualche decina di milioni di gradi Kelvin. La misura dell'intensità di raggi X emessi da tale gas e della dispersione che esso provoca sulle radiazioni che lo attraversano sarà senza dubbio di grande importanza per lo sviluppo della cosmologia nei prossimi anni.

Non si sa ancora quasi nulla sul gas intergalattico nei superammassi e nei vuoti scuri: si può solamente dire che non c'è alcuna emissione osservabile di raggi X e di radioonde, né alcun assorbimento ottico e ultravioletto delle radiazioni provenienti da quasar. Inoltre si può stabilire un limite superiore per la densità media del gas: infatti, la densità media del gas intergalattico è uguale o inferiore alla densità della materia nelle galassie mediata su tutto il volume, compreso quello intergalattico.

La densità di massa media della materia dell'universo (protoni, nuclei ed elettroni) è assai difficile da valutare: il suo valore è compreso tra 0,6 e 6 per 10³¹ g/cm³, il che significa che in media c'è un solo nucleone (protone o neutrone, libero o legato in un nucleo) ogni 3-30 m³. Per fissare le idee prenderemo come ordine di grandezza della densità numerica dei nucleoni il valore

n0_N ~ 2 × 10^-7 cm^-3,

che possiamo suddividere nella densità di protoni, np⁰ = 1,67 × 10^-7, cm^-3, e in quella di neutroni, n0_n = 0,33 × 10^-7 cm^-3. Poiché l'universo è elettricamente neutro, la densità numerica degli elettroni è uguale a quella dei protoni:

n0_e 1,67 × 10^-7 cm^-3.

La densità di energia dei barioni è il prodotto della massa del protone m_N per n⁰_Nc²:

ρ⁰_N = m_Nn0_Nc² = 3 × 10^-10 erg/cm³.

c) La radiazione di fondo a microonde.

Poiché le stelle emettono radiazioni, nello spazio che circonda le stelle e le galassie deve esserci una densità di luce stellare. Questa affermazione banale si applica anche alle radiosorgenti e alle radioonde. Nel 1964 A. A. Penzias e R. W. Wilson scoprirono l'esistenza di un altro tipo di radiazione, la cosiddetta radiazione di fondo a microonde (MBR, da Microwave Background Radiation), che nell'intervallo di lunghezze d'onda compreso tra 1 mm e 20 cm predomina nettamente sulle radiazioni combinate delle stelle e delle radiosorgenti. Essa è altamente isotropa, ossia la sua intensità è, con grandissima precisione, uguale in tutte le direzioni: sotto questo aspetto essa è ben diversa dalla radiazione emessa dalle stelle e dalle radiosorgenti. La MBR presenta la distribuzione spettrale di equilibrio (radiazione di corpo nero) che si avrebbe in una cavità le cui pareti venissero mantenute alla temperatura di 2,7 K (circa −270 °C). Poiché nell'universo non ci sono pareti e sia la nostra galassia che l'universo intero sono trasparenti alla MBR, possiamo essere sicuri che la distribuzione spettrale misurata sulla Terra coincide con quella che si misurerebbe in qualsiasi punto dell'universo, fuori dal sistema solare e anche al di là della galassia: la MBR è insomma sempre uguale in tutto l'universo. Nei prossimi capitoli mostreremo che l'origine della MBR è legata ai processi che si sono avuti nei primi stadi dell'universo.

La densità di energia ρ_γ della MBR si ottiene integrando su tutte le lunghezze d'onda il flusso specifico moltiplicato per 4π e diviso per la velocità della luce c. Il valore che si ottiene è:

ρ0_γ = 4,7 × 10^-13 erg/cm³ ~ 1,6 × 10^-3ρ0_N.

Questa densità è molto inferiore a quella della materia e, di conseguenza, all'epoca attuale l'inerzia della MBR (e anche della radiazione emessa da sorgenti discrete) è trascurabile rispetto a quella della materia e della gravitazione.

Come ha dimostrato Einstein, la radiazione elettromagnetica consiste di particelle elementari chiamate fotoni o quanti di luce. L'energia E_γ di ciascun fotone è uguale a hv, dove h è la costante di Planck e v è la frequenza della radiazione. Dalle misure sulla MBR si può dedurre il valore della densità numerica di fotoni:

n0_γ ~ 500 cm^-3 ~ 2,5 • 10⁹ n0_N.

Il numero medio di fotoni in un cm³ è dunque circa 2 miliardi e mezzo di volte maggiore del numero di barioni.

Le condizioni che esistono sulla Terra, dove c'è una forte prevalenza di materia normale (l'atmosfera a temperatura ambiente contiene 2,5 • 10¹⁹ molecole/cm³ e 5 • 10⁸ fotoni/cm³) sono l'opposto di quelle dell'universo considerato nel suo insieme, dove, sebbene i fotoni siano 2 miliardi e mezzo di volte più numerosi dei protoni e dei neutroni, la maggior parte della massa è tuttavia costituita da protoni e neutroni. Potremmo paragonare l'universo a una foresta popolata da elefanti e formiche: le formiche sono ben più numerose degli elefanti, ma sono gli elefanti che predominano nettamente come quantità di carne!

La spiegazione del valore del rapporto fra il numero dei protoni e il numero dei fotoni è un problema molto complesso; in effetti, in prima approssimazione, la teoria delle particelle elementari è simmetrica per quanto riguarda materia e antimateria e, poiché alle basse temperature la materia e l'antimateria si annullerebbero a vicenda, l'esistenza stessa di un universo composto essenzialmente di materia richiede una spiegazione: torneremo più avanti su questo problema.

d) Altri componenti dell'universo.

Accanto ai protoni e ai fotoni si è praticamente sicuri che nell'universo esistano in grande abbondanza neutrini e antineutrini di bassa energia (circa 5 • 10^-4 e V). È tuttavia difficilissimo accertare sperimentalmente l'esistenza di tali particelle, poiché la loro interazione con la materia normale è estremamente debole. Calcoli attendibili sul tasso di produzione di neutrini e antineutrini nel plasma esistente negli stadi iniziali dell'universo danno per la densità numerica dei tre tipi di neutrini corrispondenti ai tre leptoni carichi conosciuti (elettrone, muone, tau) il valore di circa 420 neutrini e antineutrini per cm³, un valore prossimo a quello della densità numerica dei fotoni.

Attualmente non si conosce sperimentalmente la massa dei neutrini, ma soltanto un limite superiore. Un esperimento, peraltro non confermato e sulla cui attendibilità sono state avanzate riserve, dava per la massa a riposo del neutrino elettronico il valore di circa 4 • 10^-32 g, ossia ventimila volte inferiore alla massa dell'elettrone. Se questo valore fosse confermato, i neutrini rappresenterebbero approssimativamente il 90% dell'intera massa dell'universo. Gli esperimenti estremamente delicati attualmente in corso per la misura della massa del neutrino permetteranno nel futuro di decidere quale sia effettivamente il contributo dei neutrini alla massa dell'universo.

Le teorie sulle interazioni fondamentali prevedono l'esistenza di numerose particelle non ancora osservate a causa della loro debolissima interazione con la materia normale. Tali particelle, se effettivamente esistenti, sarebbero senza dubbio state presenti nei primi stadi dell'universo e talune di esse potrebbero essere sopravvissute fino a oggi. Se questa congettura si dimostrerà corretta, tali particelle potrebbero fornire un contributo importante alla massa dell'universo: sebbene la loro presenza sarà ben difficilmente osservabile direttamente, gli effetti dinamici prodotti dalla loro gravità potrebbero rivelarsi di enorme importanza.

e) La massa oscura.

Come abbiamo visto nel paragrafo precedente, è possibile che una frazione notevole della massa dell'universo sia costituita da particelle inosservabili a causa della loro debolissima interazione con la materia normale e con i fotoni. Vi sono anche degli indizi di natura puramente astronomica dell'esistenza di una massa ‛oscura' o ‛mancante' nello spazio intergalattico: essi sono forniti dall'osservazione dei moti dei corpi - nubi di gas e altre galassie - nel campo gravitazionale prodotto da una data galassia. Tali osservazioni hanno dimostrato che, per produrre i moti osservati, la massa effettiva di una galassia e di tutto ciò che la circonda fino a una distanza dell'ordine di 500 kpc deve essere circa dieci volte maggiore della massa visibile della galassia stessa, cioè delle stelle e del gas contenuti entro una distanza di 30-50 kpc.

La natura di questa massa oscura è attualmente assai controversa. Per quanto riguarda le galassie sembra possibile che tale massa sia costituita da materia normale (nucleoni), anche se taluni preferiscono ipotizzare la presenza di materia esotica (neutrini, fotini, ecc.). Ancora più incerta è la natura della massa occorrente a legare gravitazionalmente le grandi strutture (ammassi e superammassi di galassie) e l'universo nel suo insieme. Torneremo più avanti su questo punto.

3. La dinamica attuale dell'universo

a) La legge di Hubble.

Le osservazioni astronomiche hanno dato fino a tempi relativamente recenti l'impressione dell'assoluta stabilità ed eternità del sistema solare nel cielo stellato. Il moto che si osserva nel sistema solare è periodico e periodico è anche il moto delle stelle nella nostra galassia. È comprensibile dunque che partendo da queste osservazioni le prime teorie cosmologiche considerassero l'universo come stazionario (immobile). La teoria di un universo in evoluzione proposta da Friedmann nel 1922 e nel 1924 rappresentò una novità inattesa e la conferma che le osservazioni di Hubble ne diedero nel 1929 si può considerare una delle scoperte scientifiche più importanti del nostro secolo. Hubble osservò che tutte le righe spettrali delle galassie lontane sono spostate verso il rosso, il che significa che la lunghezza d'onda osservata, λ_oss di ogni riga è maggiore della lunghezza d'onda λ_em della riga corrispondente del medesimo elemento chimico misurata in laboratorio. Come misura dello ‛spostamento verso il rosso' si prende solitamente la quantità

z = (λ_oss − λ_em)/λ_em, cosicché λ_oss = (1 + z)λ_em (1)

(la riga spettrale emessa da una stella ha la stessa lunghezza d'onda, λ_em, della riga spettrale osservata in laboratorio).

Le diverse righe spettrali di una data galassia sono tutte egualmente spostate verso il rosso, cioè hanno tutte lo stesso z: questo suggerisce che lo spostamento sia dovuto al moto della galassia rispetto a chi la osserva. Per piccoli valori di z la relazione che lega la velocità di recessione u del moto e lo spostamento verso il rosso z è approssimativamente

u = zc, (2)

dove c è la velocità della luce.

Hubble scoprì che lo spostamento verso il rosso - e quindi anche la velocità u - è proporzionale alla distanza che separa la galassia dall'osservatore. È questa la famosa legge di Hubble espressa dalla relazione

u = HR. (3)

La velocità u corrisponde a un allontanamento dall'osservatore, cioè u è parallela al vettore R diretto dall'osservatore alla galassia; il fattore di proporzionalità è chiamato ‛costante di Hubble' ed è indipendente dalla galassia scelta, ossia non dipende dalla direzione di R, nè dal suo modulo.

Secondo tutte le teorie cosmologiche, il rapporto u/R = H è funzione decrescente del tempo: quella che si chiama generalmente costante di Hubble, H₀, è in realtà il valore della funzione H(t) per t = t₀, dove t₀ è l'età attuale dell'universo, cioè H₀ = H(t₀). La misura di z dai dati osservativi è piuttosto semplice e la precisione a cui si può arrivare e superiore a 0,003, corrispondente a una velocità dell'ordine di 100 km/s; è invece assai difficile determinare con buona precisione la distanza R. Il valore di H₀ determinato da Hubble stesso era sbagliato di almeno un fattore cinque o dieci, ma ancora oggi gruppi diversi di osservatori danno valori di H₀ compresi nell'intervallo (50 ÷ 100) km s^-1 Mpc^-1 ossia (1,6 ÷ 3,2) × 10^-18 s^-1. Come vedremo più oltre l/H₀ è l'età dell'universo. Tenendo conto anche di considerazioni teoriche, noi siamo inclini a preferire il valore più basso, ossia 50 km s^-1 Mpc^-1, o un valore ancora più basso. Con H₀ = 50 km s^-1 Mpc^-1, una galassia con z = 0,1, che si muova cioè a una velocità di 0,1 c = 30.000 km/s, si trova a una distanza R da noi pari a 30.000/50 = 600 Mpc= 1.900 milioni di anni luce.

b) L'espansione dell'universo.

Il tempo occorrente a una galassia che si allontani da noi con velocità u per raggiungere una distanza R è

t₀ = R/u = R/H₀R = 1/H₀.

Questo tempo di espansione è lo stesso, qualunque sia la galassia scelta.

La legge di Hubble permette una semplice interpretazione del meccanismo di espansione: supponiamo che le galassie siano state tutte concentrate in un solo punto a un dato momento (t = 0) nel passato e che in quel momento abbiano incominciato ad allontanarsi dalla nostra galassia in diverse direzioni e con velocità diverse. Dopo un tempo t₀ ciascuna galassia avrà coperto una distanza R uguale a

R = u • t₀; (4)

ora, questa non è altro che la legge di Hubble letta da destra a sinistra,

u = R/t₀ = H₀R, (5)

dove t₀ = l/H₀.

Appare così evidente il legame tra la legge di Hubble e l'idea stessa dell'evoluzione dell'universo. La legge di Hubble implica infatti un'espansione sistematica della distribuzione delle galassie e l'esistenza di un istante - che abbiamo chiamato t = O - in cui la densità era molto elevata e il moto stava appena incominciando. È proprio questa ipotesi che viene confermata, almeno qualitativamente, dalle osservazioni che hanno condotto alla legge di Hubble. A prima vista sembrerebbe che la legge di Hubble privilegi una galassia - la nostra - rispetto alle altre, in quanto, mentre la prima sarebbe immobile, tutte le altre si allontanerebbero da essa. Si ha cioè l'impressione che esista un punto preciso dello spazio dal quale ha avuto inizio il movimento di tutte le galassie.

Questa conclusione, in realtà, è del tutto errata, perché l'unica caratteristica misurabile del moto è la velocità relativa. Infatti nel descrivere il moto siamo partiti dall'ipotesi che la nostra galassia, G, fosse immobile e che una data galassia lontana, g, si stesse allontanando da noi: un osservatore su quella galassia lontana, g, può invece supporre di essere lui immobile, mentre noi ci muoviamo nella direzione opposta ed è facilmente dimostrabile che quell'osservatore arriverà anch'egli a determinare la stessa legge di Hubble e, misurando molte velocità, otterrà il medesimo valore di H₀. Ne consegue che tutte le galassie sono equivalenti e che qualsiasi coppia di esse è in moto relativo: nessuna galassia si può dire immobile ed è impossibile definire un punto preciso R = O dello spazio in cui avrebbe avuto inizio l'espansione, sebbene vi sia stato effettivamente un istante preciso t = O nel quale l'espansione ha avuto inizio.

Torneremo più avanti su questo punto per discuterlo in maniera più realistica mediante la descrizione dell'universo basata sulla relatività generale.

c) L'espansione dell'universo e l'isotropia della MBR.

Passiamo ora a discutere il comportamento della radiazione di fondo a microonde (MBR) in relazione al movimento di espansione delle galassie descritto dalla legge di Hubble. In particolare ci chiediamo se la nostra galassia si muova rispetto alla MBR. È facile vedere che un moto dell'osservatore rispetto alla MBR si rivelerebbe attraverso un'anisotropia della MBR: con l'antenna orientata nella direzione del moto la temperatura risulterebbe più alta, con l'antenna orientata in direzione opposta più bassa. Una leggera anisotropia (chiamata anisotropia di dipolo) è stata in effetti osservata su grandi scale ed è spiegabile come effetto del moto del sistema solare in direzione della costellazione del Leone con velocità di 390 km/s. Più recentemente è stata anche osservata una fluttuazione annuale di tale velocità dovuta al moto della Terra attorno al Sole con velocità di 30 km/s. Infine è stato recentemente osservato un moto della nostra galassia in direzione dell'ammasso della Vergine.

Come misura dell'anisotropia della MBR sulle piccole scale si usa il rapporto fra le fluttuazioni di temperatura δT e la temperatura: il limite superiore di tale rapporto, su una scala angolare di 4,5 minuti di arco, è

Riferendosi alla MBR si parla spesso di ‛nuovo etere'. La velocità della nostra galassia rispetto alla MBR è molto piccola in confronto alle velocità che sono state misurate per alcune galassie lontane le quali sono dell'ordine di qualche decina o qualche centinaio di migliaia di chilometri al secondo.

È importante tener presente che tali galassie lontane si muovono insieme alla MBR che le circonda. Il sistema in quiete del ‛nuovo etere', ossia della MBR, è diverso in diversi punti: il moto relativo di tali sistemi di quiete obbedisce alla legge di Hubble ancora meglio di quanto non faccia il moto delle singole galassie.

Pertanto i fotoni della MBR nelle vicinanze di una galassia lontana devono presentare uno spostamento verso il rosso uguale a quello della galassia. Perché un osservatore sulla Terra possa ricevere ora la MBR a una data temperatura (2,7 K), è necessario che la temperatura della MBR sia più alta nei pressi della galassia lontana:

T = (1 + z) • 2,7 K. (6)

Il fatto che la temperatura della MBR che circonda la galassia lontana sia più alta non implica che vi sia un'effettiva differenza tra le condizioni attorno a quella galassia e le condizioni attorno alla nostra. Il fatto è che mentre la temperatura della MBR attorno alla nostra galassia, misurata oggi, è di 2,7 K, la temperatura più alta - (1 + z) 2,7 K - della MBR attorno alla galassia lontana si riferisce in realtà a un tempo precedente.

Si deve infatti tener conto del tempo t, necessario all'onda radio e alla luce per coprire la distanza R. A quel tempo precedente anche la temperatura della MBR attorno a noi era più alta. Il fatto che l'universo sia uniforme fa sì che le condizioni siano uguali dappertutto se si riferiscono al medesimo istante misurato a partire dall'istante in cui l'universo ebbe inizio. Infine si tenga presente che la legge di Hubble è valida solo per distanze sufficientemente grandi, cioè vale su larga scala. Non vale invece per oggetti legati gravitazionalmente. Per esempio, un ammasso di galassie o una galassia, compresa la nostra, non si espandono e neppure si espande l'orbita di una stella doppia né quella della Terra attorno al Sole. Tanto meno si espandono gli atomi o i campioni di lunghezza in laboratorio.

4. Relatività generale e cosmologia

a) Il modello cosmologico di Friedmann.

Lo studio delle proprietà globali dell'universo richiede l'uso delle equazioni della teoria della relatività generale, per la quale abbiamo già rinviato il lettore all'articolo relatività. Qui ci limitiamo a sottolineare alcuni risultati essenziali, che sono necessari a comprendere la struttura globale dell'universo.

La teoria della relatività generale si basa sull'ipotesi, proposta per la prima volta da Riemann, che la geometria stessa dello spazio sia determinata dalla materia presente, ossia, più precisamente, dalla densità di energia, di impulso e di tensione, cioè da quello che si chiama il tensore di energia-impulso. La relazione fra le proprietà geometriche dello spazio, riassunte in un tensore detto tensore di Einstein, e il tensore di energia-impulso è data dalle famose equazioni di Einstein, che stanno alla base della relatività generale.

Discuteremo tali equazioni nel caso particolare del modello cosmologico di Friedmann, che è basato sulle ipotesi seguenti.

1. Si suppone che l'universo sia omogeneo (cioè che in esso tutte le grandezze osservabili siano indipendenti dalla posizione) e isotropo (cioè che in esso tutte le direzioni siano equivalenti). La geometria di tale universo è determinata dalla metrica di Robertson e Walker per la quale il quadrato dell'elemento d'arco ha la forma:

La funzione a(t), detta ‛raggio di curvatura', ha le dimensioni di una lunghezza e definisce la scala della distanza, la quale perciò dipende dal tempo t; le coordinate r, θ, ϕ sono riferite a un sistema in moto con la materia; x = 0, ± 1 determina la curvatura dello spazio: x = 0 corrisponde allo spazio euclideo (piatto), x = 1 a quello ellittico chiuso, x = −1 a quello iperbolico aperto; la funzione x/a² è detta ‛curvatura'.

2. Si suppone che l'universo sia riempito uniformemente da un gas il cui tensore di energia-impulso nel sistema di riferimento in moto con la materia dipenda soltanto da due funzioni del tempo ρ(t) e P(t), che rappresentano rispettivamente la densità di energia non gravitazionale e la pressione del gas.

3. Si suppone che l'espansione avvenga a entropia costante.

Con queste tre ipotesi si può dimostrare che fra le due funzioni ρ(t) e P(t), che descrivono nel modello considerato le proprietà della materia, e il raggio di curvatura a(t), che descrive la geometria dello spazio omogeneo e isotropo, sussiste, in virtù delle equazioni di Einstein, l'equazione seguente (supporremo per semplicità che il cosiddetto ‛termine cosmologico' sia trascurabile):

dove G è la costante di Newton e c la velocità della luce. Inoltre dalla conservazione dell'energia e dell'impulso a entropia costante si deduce l'equazione:

che stabilisce l'uguaglianza fra la variazione dell'energia nel volume a³ e il lavoro fatto dalla pressione sulla superficie. Per integrare la (8) e la (9), che sono chiamate equazioni cosmologiche di Friedmann, occorre dare, oltre alle condizioni iniziali, l'equazione di stato, ossia la relazione fra la pressione P e la densità ρ.

b) La legge di Hubble e la densità critica.

L'equazione (8) mostra che, per determinare la curvatura a un dato istante, occorre conoscere a quell'istante la densità e la velocità di espansione

Quest'ultima è determinata empiricamente a t = t₀, cioè al momento attuale, dalla legge di Hubble. Infatti nel sistema di coordinate in moto con la materia la distanza fra due punti al tempo t è data da R(t) = a(t)r, dove r, adimensionale, è costante: l'aumento della distanza è dovuto all'aumento del raggio di curvatura a(t), cioè del fattore di scala con cui le lunghezze vengono misurate.

Pertanto la legge di Hubble (3) si può scrivere nella forma

dove la funzione di Hubble dipende solo dal tempo ma non dal posto.

Per mezzo della (10) la curvatura x/a² diviene

che è valida a ogni istante e in particolare all'istante attuale t₀.

L'equazione (11) suggerisce di definire una densità di energia critica ρ_c(t), legata al valore della funzione di Hubble attraverso la formula

La densità critica, che è funzione del tempo, è dunque quella corrispondente al caso di uno spazio euclideo, cioè a curvatura nulla.

Il valore attuale della densità critica, ρ0_c, è incerto a causa dell'incertezza nella misura di H₀: con i valori riportati nel cap. 3 si ottiene

ρ0_c = (1,6-0,l6) 10^-8 erg/cm³. (13)

Dalla (11) discende che, se a un certo istante t, ρ(t) > ρ_c(t), la curvatura x/a² è positiva, mentre ρ(t) 〈 ρ_c(t) implica una curvatura negativa. È inoltre evidente che il segno della curvatura resta invariato nel tempo.

Il segno della curvatura, che è in linea di principio determinabile misurando il valore attuale della costante di Hubble e quello della densità, è la caratteristica più importante della geometria dell'universo. La geometria differenziale, iniziata da Gauss, Lobačevskij e Riemann, dimostra che se il segno della curvatura è negativo l'universo è infinito o, come si dice, aperto. Al contrario un universo a curvatura positiva è finito, ossia chiuso. Occorre osservare che un universo finito non ha tuttavia confini, nello stesso modo in cui la superficie bidimensionale di una sfera immersa in uno spazio a tre dimensioni, pur essendo finita, non ha confini: partendo da un punto qualunque di una sfera e muovendosi lungo un cerchio massimo passante per quel punto si ritorna dopo un giro completo al punto di partenza.

Con un procedimento analogo a quello che si usa per calcolare la superficie di una sfera bidimensionale si può calcolare il volume di un universo chiuso, cioè a curvatura positiva. Il risultato è

V = 2 π²a³. (14)

Il raggio di curvatura di tale universo al tempo t si può esprimere facilmente a partire dalla (11) e dalla (12) per mezzo della funzione di Hubble e della densità:

dove Ω(t) = Q(t)/ρ_c(t) > 1.

Se Ω è molto prossimo a i il raggio di curvatura tende all'infinito e in particolare diviene molto più grande della regione attualmente esplorabile dell'universo, cioè

a(t₀) ≫ ct₀, (16)

dove t₀ è l'età attuale dell'universo. In questo caso l'elemento d'arco (7) assume approssimativamente la forma euclidea, cioè:

dl² = a(t²) [dr² + r²(dθ² + sen² θdϕ²)]. (17)

L'espressione (17) ci dice che nella regione osservabile dell'universo lo spazio tridimensionale è approssimativamente piatto nello stesso senso in cui la superficie di un intorno di un punto su una sfera bidimensionale è approssimativamente piatta, se la dimensione lineare dell'intorno è trascurabile rispetto al raggio della sfera.

Purtroppo al momento attuale l'incertezza sul valore della costante di Hubble, H(t₀), e sulla percentuale di materia oscura contenuta nell'universo non consente di valutare con sicurezza il valore di Ω(t₀) = Ω₀ e quindi di stabilire se l'universo sia chiuso o aperto. Si può solo dire che Ω₀ è compreso nell'intervallo

0,03 ≤ Ω₀ ≤ 2. (18)

c) Soluzioni dell'equazione di Friedmann.

L'equazione (8) può essere riscritta, utilizzando la (11), nella forma

dove a₀, ρ0_c e Ω₀ = ρ₀/ρ⁰_c rappresentano le corrispondenti grandezze al tempo t₀. Ora, se Ω_{0 >} 1, esisterà un tempo t_m, per cui (da/dt)_tm = O, dopo il quale il segno della velocità si invertirà e l'espansione si cambierà in contrazione. Viceversa, se Ω_{0 〈} 1, il secondo membro resta sempre positivo e l'espansione continuerà per sempre.

Ci limiteremo a dare la soluzione delle equazioni (8) e (9) nel caso in cui sia lecito trascurare il secondo termine nelle parentesi quadre a secondo membro della (19). Questa approssimazione è valida per t 〈 t₀ per cui a(t) > a₀ e ρ(t) > ρ0_N > ρ0_c. Inoltre ammetteremo che nell'intervallo di tempo su cui si integra la forma dell'equazione di stato P = P(ρ) resti costante. Considereremo due casi: 1) P = 0. Questa equazione è valida per materia non relativistica con densità di energia ρ ~ρ_N ≫ ρ_N ≫ ρ_γ condizione ben soddisfatta all'epoca presente t₀ e che supporremo valida in un intervallo di tempo t_{1 〈} t ≤ t₀; 2

Questa equazione è valida per la radiazione elettromagnetica e per la materia nel limite estremo relativistico. Supporremo che essa valga per t 〈 t₁, dove t₁ è definito dalla condizione

ρ_N(t₁) = ρ_γ(t₁). (20)

L'intervallo di tempo [0, t₁] è chiamato ‛epoca radiativa'. Sotto le ipotesi specificate la soluzione delle equazioni (8) e (9) si può scrivere nella forma

dove ξ = 1, per t₁ 〈 t, t′ ≤ t₀; ξ = 4/3, per t,t′〈 t₁.

Per t′ ≪ t possiamo trascurare il secondo termine a primo membro della (21), che diviene

dove

rappresenta una stima dell'età dell'universo. Mentre la dipendenza di ρ da t è la stessa nell'epoca dominata dalla materia (t₁ ≤ t 〈 t₀) e in quella dominata dalla radiazione (t 〈 t₁), la dipendenza del raggio di curvatura è invece diversa:

Servendoci di queste relazioni possiamo valutare il tempo che separa l'era dominata dalla materia non relativistica da quella dominata dalla radiazione. A tal fine osserviamo che nell'epoca non relativistica la densità varia come e ρ ≈ ρ_N ~ a^-3; invece, nell'epoca relativistica (dominata dalla radiazione), dalla conservazione dell'entropia segue che la densità varia come ρ ~ a^-4. Il valore di a per cui la densità di energia delle particelle non relativistiche eguaglia quella della radiazione è dunque

Il tempo t₁ calcolato con la (23) è

Infine osserviamo che la conservazione dell'entropia implica che la temperatura della radiazione vari come

dove l'ultima relazione è stata dedotta usando la (25). In particolare la temperatura della radiazione al tempo t₁ è

A partire dalle relazioni (23), (24) e (26), che vanno sotto il nome di ‛equazioni del modello standard', è possibile seguire nel tempo l'evoluzione dell'universo e i cambiamenti che la materia ha subito.

d) L'energia dell'universo nel caso x = 1.

Nel caso x = 1, cioè per un universo chiuso, il raggio dell'universo raggiunge un valore massimo per poi nuovamente diminuire. Il massimo si ottiene quando l'espansione si arresta (da/dt = O), ossia quando il quadrato del raggio di curvatura vale

La massa totale dell'universo definita come la somma delle masse di riposo, cioè M = ρV/c², vale (v. eq. 23)

c²M = 2π² a³ρ. (28)

La massa effettiva non è tuttavia M ma M − ΔM, dove ΔM è il decremento di massa dovuto all'energia gravitazionale. Questo effetto è simile a quello che si ha in un nucleo, la cui massa effettiva è uguale alla somma delle masse dei protoni e dei neutroni diminuita dell'energia di legame divisa per c². Si può dimostrare che il decremento di massa dovuto all'energia gravitazionale è

Osserviamo che questa espressione è del tutto naturale: la relatività generale permette di determinare il fattore 4/3 mentre il resto dell'espressione segue da semplici considerazioni dimensionali.

Utilizzando le (27)-(28) è facile allora verificare che in corrispondenza della massima curvatura la massa effettiva si annulla:

M − ΔM = 0. (30)

L'istante in cui l'universo raggiunge la massima curvatura è quello in cui l'energia cinetica dovuta all'espansione si ann+ulla: a questo istante, pertanto, c²(M − ΔM) rappresenta l'energia dell'universo. Poiché l'energia si conserva, giungiamo alla sorprendente conclusione che un universo di Friedmann a curvatura positiva ha energia nulla.

5. L'evoluzione dell'universo nell'epoca radiativa (10^-5s ≤ t ≤ 10¹³s).

a) La composizione del plasma.

Il periodo di cui ci occupiamo in questo capitolo, periodo nel quale si è determinata la composizione chimica dell'universo, è limitato superiormente dal tempo t₁ ≃ 3 × 10¹³s, subito prima del quale il maggior contributo alla densità di energia viene dalla radiazione e dalle particelle relativistiche e l'equazione di stato è dunque P = (1/3) ρ. Il limite inferiore è t₄ = 10^-5 − 10^-6 s, subito prima del quale esistono nell'universo particelle (quarks, gluoni, ecc.) il cui comportamento non è stato ancora ben chiarito da esperienze di laboratorio (v. Weinberg, 1977).

Durante questo periodo il fattore di scala varia come a(t) ~ t^1/2 e la temperatura come T(t) ~ t^-1/2 (v. eqq. 25 e 26), passando da T₄ = T(t₄) ≃ (3 × 10⁸-10⁹) eV/k a T₁ = T(t₁) = 0,3 eV/k (k indica la costante di Boltzmann: 1 eV/k = 1,16 × 10⁴K).

Le leggi elementari in questo intervallo di temperatura sono ben note, ma questo non significa tuttavia che il comportamento della materia dell'universo possa essere descritto con assoluta sicurezza. Infatti i fenomeni collettivi di cui in questi anni si va scoprendo l'importanza potrebbero alterare profondamente le conseguenze tratte da una descrizione che ignori tali effetti. Pur tenendo presente queste cautele possiamo ragionevolmente supporre che ‛all'inizio del periodo di cui ci occupiamo l'universo fosse costituito da un plasma essenzialmente uniforme alla temperatura di circa 3 × 10⁸ eV/k, nel quale erano presenti protoni (p), antiprotoni (ä), neutroni (n), antineutroni (ò), mesoni (π⁺, π^-, π°), elettroni (e^-), positroni (e⁺), neutrini (ν, antineutrini (ν̄), fotoni (γ) oltre a una piccola percentuale di particelle e antiparticelle strane. All'inizio di questo periodo tutte le particelle, eccetto nucleoni e antinucleoni, avevano energie relativistiche. Fra di esse avvenivano reazioni di creazione e annichilazione del tipo

Affinché queste reazioni siano all'equilibrio, occorre che la velocità di reazione sia maggiore di quella di espansione dell'universo, cioè che si abbia

dove

è il tempo di reazione, che dipende da T attraverso la sezione d'urto σ, la densità numerica n e la velocità relativa v. Il tempo di espansione al secondo membro della (32) è definito dalla relazione

nella quale la seconda uguaglianza si ottiene dalla (8) trascurando il termine di curvatura.

Quando la (32) è soddisfatta, è facile determinare, con i metodi usati per studiare gli equilibri delle reazioni chimiche, i rapporti fra le densità numeriche dei componenti del plasma, i quali dipendono soltanto da T e dagli spins delle particelle reagenti. In questo modo si trova che intorno al tempo t ~ 10^-3, quando T ≃ 30 MeV/k (1 MeV = 10⁶ eV), le densità numeriche delle particelle leggere erano circa eguali:

n_γ ≃ n_e+ ≃ n_e- ≃ n_ν ≃ n_ν̄ ~ 100³⁶ cm^-3. (34)

La densità numerica dei nucleoni n_N era invece circa 10⁹ volte minore, cioè il rapporto n_γ/n_N si è mantenuto approssimativamente costante. Tuttavia, mentre nell'universo attuale il maggior contributo alla densità di energia proviene dai nucleoni, al tempo t =i 10^-3 s la densità di energia delle particelle leggere era molto maggiore di quella dei nucleoni. Trascurando quest'ultima, la densità di energia si può dunque scrivere nella forma

che è simile a quella del gas di fotoni. Il fattore statistico g(T) (che per il gas di fotoni vale 2) dipende dagli spins delle particelle presenti; nell'intervallo di temperature 0,3 eV/k ≤ T ≤ 10⁸ eV/k, g(T) varia fra 10 e 50.

b) La scomparsa degli antinucleoni.

In generale il tempo di reazione τ_r(T) cresce al decrescere di T più rapidamente del tempo di espansione, che varia come T_e ~ T^-2. Pertanto, quando la temperatura scende sotto un certo valore (caratteristico di ciascuna reazione), la condizione di equilibrio (32) cessa di essere soddisfatta e le particelle che prendevano parte alla reazione si disaccoppiano, cosicché i rapporti fra le loro densità restano da quel momento in poi congelati.

La prima reazione a uscire dall'equilibrio è la creazione di coppie nucleone-antinucleone da parte di pioni o di fotoni. Questo avviene, secondo i calcoli di Ja. B. Zeldovich (v. Zeldovich e Novikov, 1983), quando la temperatura scende al disotto di T_N ≃ 20 MeV/k, cioè a un tempo t_N ≃ 2,5 × 10^-3 s; da quel momento in poi la creazione di coppie non riesce più a compensare l'annichilazione e nucleoni e antinucleoni scompaiono rapidamente.

Se si suppone, come sembrerebbe naturale, data la simmetria delle interazioni elettromagnetiche e forti rispetto allo scambio di nucleoni e antinucleoni, che inizialmente vi fosse un ugual numero di nucleoni e antinucleoni, è p0ssibile determinare le densità numeriche n_N e n-_N all'istante t_N in cui l'equilibrio si è rotto; il risultato che si ottiene è

n_N(t_N) = n-_N(t_N) ≃ 2 × 10^{18 cm-3}.

Poiché attualmente la densità numerica dei nucleoni è molto maggiore di quella degli antinucleoni, è necessario ammettere che già per t 〈 t_N la densità numerica dei nucleoni fosse superiore a quella degli antinucleoni: n_N = n-_N + δn_N. È essenzialmente a quest'eccesso ònN, sopravvissuto all'annichilazione, che è dovuta la densità attuale n0_N dei nucleoni e la stessa esistenza dell'umanità. Ritorneremo sulla causa di questa asimmetria nel capitolo seguente.

c) Il congelamento delle interazioni deboli.

Il processo più importante nel periodo che va da t = 10^-3 s a t = t₃ = 1 s è la trasformazione di protoni in neutroni e viceversa per effetto delle reazioni

p + e^- ⇄ n + ν e e^* + n ⇄ p + ν̄, (36)

simili a quelle che provocano i decadimenti β nei nuclei, cioè a quelle causate dalle interazioni deboli.

Il rapporto fra il numero di neutroni e di protoni derivante da tale processo ha delle conseguenze importanti per i processi nucleari successivi. Nell'intervallo di tempo preso in esame la trasformazione dei protoni in neutroni e quella inversa erano molto rapide e perciò il plasma era in condizioni di equilibrio termodinamico.

Tuttavia, quando intorno a t₃ = s la temperatura del plasma scende intorno a i MeV/k, il tempo di reazione τ_r delle reazioni (36) e delle altre reazioni deboli diventa inferiore al tempo di espansione. I neutrini perciò si disaccoppiano dalle altre particelle e riempiono l'universo come i fotoni della radiazione di fondo. La densità numerica attuale dei neutrini è prossima a quella dei fotoni, mentre la loro temperatura è un poco inferiore a quella della radiazione di fondo (T_0ν ~ 0,7 T_0γ ≃ 1 7 × 10^-4 eV/k). Data la debolissima interazione dei neutrini con la materia è estremamente difficile rivelare la presenza di questa radiazione neutrinica di fondo.

Dopo il congelamento delle interazioni deboli (36), il rapporto fra le densità numeriche dei protoni e dei neutroni è determinato esclusivamente dalla differenza di massa delle due particelle: a T = 0,9 MeV/k si ha n_p/n_n ≃ 5,5. Il valore di questo rapporto ha delle conseguenze importanti sulla percentuale di He⁴ presente nell'universo.

Quasi contemporanea al congelamento delle interazioni deboli è la rottura dell'equilibrio della reazione e⁺ + e^- ⇄ 2γ, con la conseguente scomparsa delle coppie e⁺, e^-. Anche in questo caso, però, una piccola percentuale di elettroni, esattamente uguale a quella dei protoni, è sopravvissuta, cosicché l'universo è elettricamente neutro.

d) La formazione dell'He⁴.

Nel periodo compreso fra il momento del congelamento delle interazioni deboli (t₃ ≃ 1 s) e t₂ ≃ 3 minuti, che segna la fine delle reazioni nucleari, i neutroni e i protoni presenti nel plasma diedero origine alla formazione di deutoni (d) secondo la reazione

n + p → d + γ. (37)

I deutoni, a loro volta, attraverso una catena di reazioni simili a quelle che avvengono ancora oggi nel Sole, si trasformarono in He⁴. Questo nucleo - la particella α - è molto stabile e costituisce il prodotto finale delle reazioni nucleari cosmologiche. La maggior parte dei neutroni sopravvissuti all'annichilazione è dunque finita nei nuclei di He⁴, mentre i rimanenti, attraverso un decadimento β, si sono trasformati in protoni.

Si può dimostrare che la quantità di He⁴ prodotta nelle reazioni nucleari durante questo periodo è una funzione decrescente del rapporto T³/ρ, dove T e ρ sono la temperatura e la densità dei protoni e dei neutroni all'epoca in cui l'He⁴ è stato formato. Ora questo rapporto, che è proporzionale all'entropia del gas di fotoni divisa per il numero totale dei protoni e dei neutroni presenti, si mantiene costante durante l'espansione dell'universo. Pertanto l'abbondanza di He⁴ cosmologico, cioè la quantità di He⁴ originata dalle reazioni avvenute fra t = 1 s e t = 3 minuti, oggi presente nell'universo è funzione del rapporto T³₀/ρ₀ fra il cubo della temperatura della MBR e la densità attuale dell'universo. Poiché T₀ è conosciuto, misurando l'abbondanza di He⁴ si può determinare ρ₀ e confrontare il valore così ottenuto con quello osservato.

Non tutto l'He⁴ esistente oggi è di origine cosmica: altro elio è stato formato nelle reazioni nucleari che avvengono all'interno delle stelle. Per confrontare l'abbondanza di elio cosmologico con quella che si deduce dalla misura di T0³/ρ₀ occorre perciò valutare la quantità di He⁴ prodotta nelle stelle e sottrarla da quella effettivamente misurata. Secondo stime attendibili quest'ultima costituisce il 22-24% della massa visibile dell'universo, in buon accordo con il valore calcolato usando per la densità dell'universo il valore ρ₀ = (4 − 8) × 10^-31 g/cm³. La maggior parte dei deutoni prodotti nella reazione (37) sono stati trasformati in He⁴ per effetto di successive reazioni nucleari. Una piccola frazione è tuttavia sopravvissuta e per questa si può ripetere il discorso precedentemente fatto per l'He⁴. Osserviamo da ultimo che il rapporto fra la densità dell'H e quella dell'He⁴ dipende dal numero di specie di neutrini. Il valore osservato è in accordo con l'ipotesi che esistano solo le tre specie di neutrini finora osservati, cioè V_e, V_μ, V_τ,. L'osservazione di altri tipi di neutrini porrebbe in difficoltà la teoria della formazione dell'elio.

In conclusione si può dire che la teoria della nucleosintesi cosmologica dà una spiegazione delle abbondanze dell'He⁴ e del deuterio (e anche dell'He³ e del Li⁷), che trova una conferma soddisfacente nei dati osservativi. Questa concordanza a sua volta offre una conferma delle ipotesi fatte sulle condizioni del plasma all'epoca in cui la nucleosintesi ha avuto luogo.

e) Le ultime fasi dell'evoluzione dell'universo.

Prendiamo infine in esame l'intervallo di tempo compreso tra la fine delle reazioni nucleari, t₂ ≃ 3 minuti, e t₁ ≃ 10⁶ anni ≃ 3 • 10¹³ s. Durante questo periodo la composizione del plasma - e^-, p, He⁴, γ - rimane quella determinata dai processi avvenuti entro i primi tre minuti e nessuna nuova particella viene distrutta o creata; ovvero, per essere più precisi, l'assorbimento e la creazione di fotoni si compensano e l'equilibrio numerico non è alterato dall'espansione. Soltanto l'energia media dei singoli fotoni diminuisce lentamente con il progredire dell'espansione, mentre i rapporti numerici tra fotoni, protoni, nuclei di elio, elettroni, neutrini e altre eventuali particelle tuttora sconosciute rimangono invariati. Cambiano invece i rapporti tra le densità di energia ρ delle varie componenti. I protoni, i nuclei e gli elettroni si muovono lentamente e perciò la loro energia, che è molto vicina alla massa di riposo moltiplicata per c², non cambia in maniera apprezzabile durante l'espansione. L'energia dei fotoni diminuisce invece progressivamente. Se i neutrini avessero una massa non nulla, poniamo di 30 elettronvolt, essi avrebbero all'inizio energie relativistiche, per poi passare a un regime non relativistico quando il plasma si fosse sufficientemente raffreddato. Mentre nel primo regime - cioè quello relativistico - la loro densità di energia varierebbe come V^-4/3, ossia come quella dei fotoni, nel regime non relativistico essa diminuirebbe in condizioni di equilibrio termodinamico come V^-1, cioè come quella dei protoni. Quando i neutrini (massicci) avessero raggiunto energie non relativistiche la densità totale del plasma sarebbe determinata principalmente dai neutrini.

Se nel plasma fossero esistite altre particelle più pesanti, ma meno numerose, come predicono alcune attuali teorie, esse avrebbero raggiunto il regime non relativistico prima dei neutrini e soltanto molto più tardi questi sarebbero venuti a costituire la parte principale della densità della massa.

Una proprietà fondamentale di queste particelle massicce che non interagiscono con la materia è che quando esse divengono non relativistiche la loro densità numerica non diminuisce al crescere del volume. Ciò significa che esse non sono più in equilibrio termodinamico: sotto questo punto di vista il loro comportamento è diverso da quello degli elettroni, dei positroni, dei protoni e degli antiprotoni. In definitiva, la spiegazione della diversità di comportamento di queste particelle rispetto a quella di p e ä, ē ed e⁺ sta nel fatto che esse interagiscono assai debolmente e che il loro tempo di rilassamento (annichilazione o decadimento) è molto superiore all'età dell'universo.

Infine, quando intorno a t₁ ~ 10⁶ anni ≃ 3 • 10³ s la temperatura del plasma scende intorno a T₁ = 0,3 eV/k, l'equilibrio della reazione

e^- + p ⇄ H + γ (38)

si rompe. Gli elettroni si legano perciò ai protoni per formare atomi di idrogeno e il gas di atomi neutri di idrogeno e di elio (quest'ultimo si è neutralizzato prima) diventa così praticamente trasparente alla radiazione. I fotoni disaccoppiati dalla materia si propagano liberamente nell'universo e costituiscono oggi la radiazione isotropa di fondo. L'epoca radiativa ha così fine: da quel momento in poi la densità di energia della materia predomina su quella della radiazione.

6. La fisica delle prime fasi dell'esistenza dell'universo.

In questo capitolo discuteremo brevemente i fenomeni fisici che, secondo le più recenti speculazioni teoriche, sono avvenuti nell'universo durante il brevissimo periodo che va da t = 10^-5 fino al tempo di Planck

dove G è la costante di Newton e ℏ quella di Planck divisa per 2π. La ragione per arrestare l'indagine a t_p, anziché spingerla fino a t = 0, sta nel fatto che prima di tale epoca la densità di energia doveva essere superiore a

In condizioni così estreme la teoria della relatività generale deve necessariamente essere sostituita da una teoria quantizzata della gravitazione, attualmente ancora sconosciuta. Non ha pertanto senso al momento attuale parlare dell'evoluzione dell'universo per t 〈 t_p.

Durante il periodo che va da t = 10^-5 s a t_P = 0,5 × 10^-43 s la temperatura dell'universo è variata di circa 20 ordini di grandezza, passando da T ≃ 10⁸ eV/k a T = T_P = 1,22 × 10²⁸ eV/k. Per descrivere il comportamento della materia a temperature così elevate occorre fare appello a teorie non ancora verificate sperimentalmente e che, verosimilmente, neppure potranno esserlo nel prossimo futuro.

Il lettore deve quindi essere avvertito che questo capitolo e quelli seguenti, i quali riflettono il frutto di speculazioni recentissime, hanno un carattere assai più ipotetico dei precedenti: gli sviluppi futuri potranno forse cambiare, in maniera anche sostanziale, l'immagine che oggi ci facciamo dei primissimi istanti della vita dell'universo.

a) La comparsa dei quarks liberi.

Come primo esempio di un fenomeno del quale non abbiamo conoscenza sperimentale diretta consideriamo quanto avvenne probabilmente quando l'età dell'universo era intorno a t = t₄ ≃ 10^-5 s e la sua temperatura era circa T = T₄ = (2-3) 10⁸ eV/k. Un semplice calcolo mostra che a quella temperatura la densità numerica dei quarks liberi è uguale a quella dei quarks confinati, come nella materia normale, in nucleoni. Nel limite relativistico la densità numerica dei quarks e degli antiquarks liberi è data da un'espressione analoga a quella valida per i fotoni, cioè

dove il peso statistico g 2 × 3 × 2 è il prodotto dei gradi di libertà di spin (2), di colore (3) e di sapore (2). Il fattore 3/4 nella (39) tiene conto del fatto che i quarks sono fermioni. Con questo valore di g e ponendo T = 10⁸ eV/k, si ottiene

n_q = n-_q ≃ (2 - 3)10³⁹ cm^-3,

cioè un valore uguale a quello dei quarks nella materia nucleare.

È pertanto probabile che a questa temperatura la materia subisca una transizione di fase simile a quella che si ha nel passaggio fra la fase liquida e quella gassosa. Per temperature T 〈 T₄ = 10⁸ eV/k, cioè per t > 10^-5 s, la materia si trova nella fase nucleare normale, immersa in un denso gas di fotoni, mentre, per T > T₄, si ha un plasma di quarks e antiquarks liberi, immersi in un gas di gluoni e fotoni. E importante notare che, mentre nella fase normale (a temperature superiori a circa 10⁶ eV/k) la densità di energia è essenzialmente uguale a quella dei fotoni (ρ ~ ρ_γ), nel plasma di quarks e gluoni il maggiore contributo alla densità di energia viene da queste particelle (e ρ ~ ρ_q-_qq), proprio in virtù del maggior numero di gradi di libertà di questi componenti. Il passaggio fra le due fasi corrisponde alla liberazione di gradi di libertà dei quarks e dei gluoni, che a bassa temperatura sono congelati nei nucleoni e non contribuiscono quindi all'entropia. Questo fa sì che nel passaggio dalla materia nucleare al plasma di quarks e gluoni si abbia un considerevole aumento della densità di entropia.

È probabile che fra non molto sarà possibile investigare sperimentalmente la natura precisa di questa transizione di fase, che dovrebbe prodursi anche nelle collisioni di ioni pesanti, ad alta energia. Esperimenti del genere saranno presto effettuati al CERN e in altri laboratori, dove saranno accelerati ioni di massa intorno a quella dell'ossigeno, con energie, nel sistema del laboratorio, fino a circa 200 GeV/nucleone. Questi esperimenti permetteranno forse di decidere se la transizione di fase che ha avuto luogo intorno a t ~ 10^-5 s abbia potuto condurre, come è stato suggerito, alla produzione di forme esotiche di materia o alla formazione di buchi neri o se invece, come altri pensano, non abbia avuto conseguenze di interesse astrofisico.

b) L'unificazione delle interazioni fondamentali.

Subito prima della transizione di fase discussa nel paragrafo precedente, cioè per t 〈 10^-5 s, l'universo era costituito da un plasma omogeneo relativistico composto essenzialmente da: a) quarks, antiquarks, gluoni; b) leptoni, cioè elettroni, muoni, leptoni pesanti, con i corrispondenti neutrini e antineutrini; c) fotoni.

Secondo le teorie attuali le proprietà delle interazioni che si esercitano fra queste particelle variano all'aumentare della temperatura. Quando questa raggiunge il valore T₆ ≃ 10²³ eV/k, le differenze fra le varie interazioni (esclusa quella gravitazionale) scompaiono, mentre aumenta la simmetria degli stati di equilibrio.

Il fenomeno avviene in due stadi: 1) l'unificazione elettrodebole, cioè quella delle interazioni elettromagnetiche e deboli, si produce a una temperatura T₅ ≃ 10¹¹ eV/k corrispondente a un tempo t₅ ≃ 2 × 10^-12 s. Questa temperatura è accessibile alle esperienze di laboratorio e i fenomeni previsti dalla teoria (v. Weinberg, 1967; v. Salam, 1969) sono stati verificati recentemente al CERN. L'unificazione elettrodebole corrisponde a un cambiamento del gruppo di simmetria. Al disotto di T₅ tale gruppo è SU(3)_c × SU(1), prodotto diretto del gruppo di simmetria delle interazioni forti (il gruppo SU(3)_c e dei gradi di libertà di colore) per quello delle interazioni elettromagnetiche (U(1)). Al disopra di T₅ il gruppo di simmetria è invece SU(3) × SU(2) × U(1), dove SU(2) × U(1) è il gruppo di simmetria dell'interazione unificata elettrodebole. Non è attualmente chiaro quali siano le conseguenze cosmologiche di questo cambiamento della simmetria; 2) l'unificazione elettronucleare, chiamata anche ‛grande unificazione', cioè quella delle interazioni elettrodeboli e forti (nucleari), dovrebbe prodursi a una temperatura T₆ ≃ 10²³ eV/k assolutamente inaccessibile alle esperienze di laboratorio. A questa temperatura le differenze fra interazioni elettromagnetiche, deboli e forti dovrebbero scomparire, mentre il gruppo di simmetria passa da SU(3) × SU(2) × U(1) a un gruppo G che contiene il precedente come sottogruppo. Quale sia questo gruppo G non è oggi noto: l'ipotesi proposta da H. M. Georgi e S. L. Glashow (v., 1974), che G vada identificato con SU(5), sembra essere incompatibile con il limite inferiore sperimentale della vita media del protone. È importante osservare che le variazioni di simmetria che avvengono a T₅ e T₆ non sono prodotte da cause asimmetriche esterne, avvengono cioè spontaneamente.

Il fenomeno è qualitativamente simile a quello che si verifica nella materia normale nel passaggio dalla fase solida, la cui simmetria è quella di uno dei gruppi cristallografici, alla fase liquida, il cui gruppo di simmetria è il gruppo euclideo. Nella transizione inversa da liquido a solido si parla di rottura spontanea della simmetria, dove l'aggettivo ‛spontaneo' sta a indicare che il cambiamento di simmetria non è dovuto all'intervento di alcuna causa esterna di asimmetria. La differenza fra la variazione di simmetria che si ha al punto di fusione di un solido e quelle che si producono nel plasma di quarks e gluoni a T₅ e T₆ sta nel fatto che nel primo caso quella che cambia è una simmetria geometrica, mentre nel caso dell'unificazione delle interazioni la simmetria che varia è quella relativa ai gradi di libertà interni.

Affinché la teoria dell'unificazione elettrodebole dia luogo al fenomeno della rottura spontanea occorre che esistano dei campi scalari, detti campi di Higgs, i quali per altro non sono ancora stati osservati. Tali campi devono annullarsi nella fase simmetrica, mentre quando almeno uno di essi acquista un valore non nullo la simmetria si rompe.

È possibile formulare la teoria in maniera tale che i campi di Higgs abbiano valore diverso da zero nello stato in cui la densità di energia è minima, cioè nello stato di vuoto. Quando la temperatura raggiunge il valore T₆ i campi di Higgs si annullano e compare la fase simmetrica. La massa delle particelle corrispondenti ai campi di Higgs è approssimativamente uguale a kT₆/c².

c) L'instabilità del protone e l'asimmetria barionica dell'universo.

Una delle conseguenze più interessanti della teoria dell'unificazione elettronucleare, dal punto di vista cosmologico, è la possibilità della non conservazione del numero barionico B, cioè della differenza fra il numero dei barioni (fermioni che interagiscono fortemente) e quello degli antibarioni. Invero la teoria prevede l'esistenza di numerosi bosoni vettoriali X che, interagendo con i quarks (q), possono cambiarli in leptoni (l) secondo la reazione

q + X → I, (40)

che viola la conservazione del numero barionico.

Questo fa sì che ad alte temperature, T ≥ T₆, la distinzione fra quarks e leptoni scompaia (il che rende conto delle tante analogie esistenti fra questi componenti elementari della materia), rendendo possibile il decadimento del protone, per esempio nel canale

p → e⁺ + π° (41)

Il valore predetto per la vita media di questo decadimento secondo SU(5) è inferiore al limite sperimentale

(p → e⁺ + π° ≥ 10³² anni,

il che non esclude però la possibilità di altri modelli unificati con diversi gruppi di simmetria. Attualmente sono in corso esperimenti più precisi per rivelare il decadimento del protone nel canale (41) o in altri canali. L'osservazione di un tale decadimento rappresenterebbe una conferma sperimentale delle teorie unificate. Come ha dimostrato A. D. Sacharov (v., 1967), perché la non conservazione di B conduca alla formazione di stati stabili con B ≠ 0, occorre che siano presenti interazioni che violino l'invarianza rispetto al prodotto della coniugazione di carica per l'inversione spaziale (CP) e che inoltre l'equilibrio termodinamico sia in qualche momento rotto. L'esistenza di interazioni che violano CP è nota sperimentalmente; nel prossimo capitolo discuteremo un modello nel quale la rottura dell'equilibrio termodinamico si realizza in maniera naturale. Si realizzerebbero così le condizioni necessarie per la produzione di stati con valori non nulli di B.

La teoria unificata dovrebbe permettere di calcolare il valore del rapporto n_N/n_γ che, come abbiamo visto nel cap. 2, vale all'incirca 10^-10. Il valore di questo rapporto dipende dal gruppo di unificazione G e non può al momento essere predetto con sicurezza.

La non conservazione del numero barionico B offre la possibilità di spiegare perché l'universo attuale si trovi in uno stato con un valore di B tanto elevato B ≃ 10⁷⁸. Se B fosse esattamente conservato, un universo che avesse avuto inizio nello stato simmetrico B = 0 avrebbe dovuto rimanere per sempre in tale stato, e perciò dovrebbe oggi essere composto di materia e antimateria in quantità uguali. La vita in tale universo sarebbe evidentemente impossibile.

Pertanto, a meno di ammettere condizioni iniziali violentemente asimmetriche, l'esistenza stessa dell'universo asimmetrico attuale sembra richiedere che a qualche istante della sua evoluzione la simmetria fra barioni e antibarioni si sia spontaneamente rotta e il valore di B sia passato da 0 al valore attuale B ≃ 10⁷⁸. È stato perciò suggerito che l'esistenza del nostro universo asimmetrico rappresenti la dimostrazione più evidente della teoria dell'unificazione elettronucleare, la quale prevede che il numero barionico non sia esattamente conservato.

Oltre alla teoria unificata, cui abbiamo brevemente accennato, esistono altre teorie, dette ‛supersimmetriche', che, oltre alla G-simmetria, prevedono l'esistenza di un'ulteriore simmetria fra fermioni (particelle a spin semidispari) e bosoni (a spin intero). Per l'astrofisica l'interesse di queste teorie sta nel fatto che esse predicono l'esistenza di nuove particelle con statistica opposta a quella delle corrispondenti particelle normali. Molte di queste nuove particelle dovrebbero essere stabili e potrebbero quindi rappresentare uno dei componenti della massa oscura. Attualmente non esiste alcuna verifica sperimentale di queste teorie.

Un'altra conseguenza di alcune teorie unificate è la possibilità che i neutrini abbiano massa non nulla. Questa previsione non può al momento considerarsi verificata, perché il valore di 30 eV annunciato recentemente da un gruppo di sperimentatori nell'Unione Sovietica non è stato confermato da altre esperienze simili. Nonostante l'enorme difficoltà di queste misure, è da sperare che presto si potrà conoscere il valore della massa del neutrino o almeno ridurre considerevolmente l'attuale limite superiore sperimentale di circa 20 eV.

7. L'espansione esponenziale

Nei capitoli precedenti si è supposto che in tutto il tempo che precedette il disaccoppiamento della radiazione, cioè per t 〈 t₁ ~ 3 • 10¹³ s, l'equazione di stato sia stata quella della materia in condizioni relativistiche estreme, cioè

dove g(T) è il peso statistico che, all'aumentare della temperatura, varia approssimativamente fra 10 e 100, per effetto della liberazione di nuovi gradi di libertà.

Come abbiamo visto nel cap. 4, la dipendenza temporale del fattore di scala a e quella della temperatura T, che si deducono da questa equazione di stato, sono quelle del cosiddetto modello standard e cioè

a(t) ~ t^1/2; T(t) ~ t^-1/2. (43)

In questo capitolo mostreremo che l'ipotesi che il modello standard (43) valga in tutto l'intervallo t_p ≤ t ≤ t₁ rende estremamente difficile giustificare: 1) l'isotropia osservata della radiazione elettromagnetica di fondo, dell'ordine di una parte in 10⁴ (problema dell'orizzonte); 2) il fatto che la geometria dell'universo visibile non si discosti troppo da quella euclidea (problema della curvatura).

Mostreremo poi come sia possibile risolvere queste due difficoltà ammettendo che le (43) siano sostituite, per un brevissimo intervallo di tempo nell'intorno di t₆ ≃ 10^-35 s, da andamenti esponenziali (modello inflazionistico) e indicheremo come questi andamenti siano in effetti suggeriti dalla teoria unificata discussa nel cap. 6.

a) Il problema dell'orizzonte.

Questo problema consiste nel trovare una spiegazione al fatto che la radiazione di fondo è attualmente isotropa su una scala di 4,5 minuti di arco (δT/T ≤ 10^-4) su distanze dell'ordine di d₀ ≃ 2ct₀, dove t₀ ≃ 5 • 10¹⁷ s è l'età dell'universo.

Sembra ragionevole richiedere che tale isotropia sia dovuta all'interazione con la materia anziché essere il risultato di artificiose condizioni iniziali. Ora, tale interazione (v. cap. 5) è cessata al tempo t₁ ≃‛ 3 • 10¹³ s, dopo il quale la radiazione si è propagata liberamente. La radiazione doveva perciò già essere isotropa al tempo t₁ e doveva esserlo su una distanza

(Si ricordi che per t₁ ≤ t ≤ t₀ il fattore di scala varia come a(t) ~ t^2/3: v. eq. 24).

Nel modello standard l'universo non poteva aver raggiunto l'isotropia al tempo ti su una distanza d₁ per effetto di interazioni causali, cioè propagantisi con velocità non superiore a c. Per vederlo definiamo l'orizzonte h(t) al tempo t, di un osservatore in moto con la materia, mediante la relazione

L'orizzonte h(t) è dunque il raggio della sfera che contiene tutti gli osservatori che hanno potuto scambiarsi segnali con velocità non superiore a c, cioè l'insieme degli osservatori causalmente connessi. La richiesta che l'isotropia al tempo ti su una distanza d₁ sia il risultato di interazioni causali è dunque espressa dalla condizione

h(t₁) 〈 d₁. (46)

Ora, nel modello standard si ha

h(t) = 2ct. (47)

Pertanto la condizione (46) diviene nel modello standard

che è ovviamente violata, poiché il secondo membro della (48) vale ~ 27.

L. van Hove (v., 1984) ha dimostrato che la condizione (46) ha delle conseguenze importanti sulle prime fasi dell'espansione dell'universo. Supponiamo infatti che il modello standard sia valido per t ≤ t ≤ t₁, mentre cada in difetto per t ≤té, dove té è un tempo maggiore di t_p. Dalla condizione (46) si deduce allora la diseguaglianza

dove si è usata la relazione î(t) = a(t)/2t valida nel modello standard.

Ora, il modello standard è certamente valido almeno fino a t ~ 10^-10 s, quando la temperatura era non superiore a 10¹¹ eV/k. Il secondo membro della (49) è quindi non minore di 10¹². Questo mostra che per spiegare l'isotropia della radiazione di fondo l'orizzonte al tempo i doveva essere almeno di 12 ordini di grandezza più grande di quello calcolato supponendo che il modello standard valga fino a t = 0.

L. van Hove (ibid.) ha dimostrato che la diseguaglianza (49) può essere soddisfatta soltanto se l'energia ρa³ contenuta nel volume a³ è aumentata di almeno 12 ordini di grandezza nelle fasi iniziali dell'espansione. Se la pressione è positiva, questo aumento di energia è incompatibile con l'equazione (9), che esprime la conservazione dell'energia non gravitazionale a entropia costante. Si giunge così al seguente risultato di natura del tutto generale. Per spiegare l'isotropia della radiazione di fondo come risultato di interazioni causali occorre che il modello standard sia stato violato nelle prime fasi dell'espansione in almeno uno dei seguenti modi: 1) la pressione sia stata negativa, P 〈 0; 2) siano intervenuti dei processi irreversibili, cioè vi sia stata produzione di entropia; 3) vi sia stata conversione di energia gravitazionale in materia.

Come vedremo nel È c, le attuali teorie inducono a ritenere che la causa della violazione del modello standard sia la pressione negativa dovuta a una transizione di fase di prima specie con sopraraffreddamento accompagnata da sviluppo di entropia.

b) Il problema della curvatura.

Il valore attuale del rapporto Ω = ρ/ρ_c, dove ρ_c è la densità critica (corrispondente a curvatura nulla), è compreso (v. eq. 18) fra 0,03 e 2. Da questo limite segue che attualmente vale la diseguaglianza

L'universo attuale è dunque piatto o approssimativamente piatto. Questo fatto non è facilmente spiegabile con il modello standard. Invero è facile vedere che le equazioni (8) e (12) implicano che, nel modello standard, ∣ρ −ρ_c∣ρ_c aumenti proporzionalmente a t. Pertanto

dove t_p, = 0,5 • 10^-43 s è il tempo di Planck. Perciò, a meno di non ammettere che il valore di Ω al tempo di Planck sia stato scelto con incredibile precisione, è difficile spiegare il suo valore attuale. Questa difficoltà va sotto il nome di ‛problema della curvatura'.

c) L'espansione esponenziale.

Recentemente D. Kazanas (v., 1980) e A. Guth (v., 1981) hanno indipendentemente suggerito un modello, che discende in maniera naturale dalla teoria dell'unificazione elettronucleare, il quale consente di superare le difficoltà illustrate nei paragrafi precedenti. Questo modello, chiamato inflazionistico, conduce a sostituire per un tempo Δt ~ 10^-21 s un'espansione esponenziale nel tempo a quella in t^1/2 del modello standard.

Consideriamo la transizione di fase che avviene a t₆ ≃ 10²³ s alla temperatura T₆ ≃ 10²³ eV/k, nella quale si rompe la G-simmetria. La transizione può essere del primo ordine e, scegliendo opportunamente i parametri della teoria, è possibile fare in modo che essa avvenga a una velocità molto minore di quella dell'espansione. In questo caso la fase G-simmetrica può mantenersi in uno stato metastabile anche molto al disotto di T₆. Il fenomeno è analogo a quello che si produce quando si diminuisce molto lentamente la temperatura dell'acqua: in queste condizioni è possibile mantenerla nella fase liquida (simmetrica) fino a circa −20 °C (acqua sopraraffreddata). Negli stati metastabili la pressione non deve necessariamente essere positiva: il fatto che appena si forma nell'acqua sopraraffreddata un granello di ghiaccio questo cresca rapidamente dimostra che la pressione dell'acqua è inferiore a quella del ghiaccio e poiché la pressione del ghiaccio è piccola, quella dell'acqua sopraraffreddata può essere negativa.

Consideriamo ora la transizione di fase che avviene a T₆ e supponiamo che essa avvenga tanto lentamente da permettere a una piccola ‛bolla' di materia di restare nella fase G-simmetrica ben al disotto di T₆. Poiché nella bolla la materia è G-simmetrica, i campi di Higgs mantengono il valore zero; in questo stato, chiamato ‛falso vuoto', la densità di energia proviene essenzialmente dai campi di Higgs, mentre la densità di energia termica è trascurabile.

Questo stato, come quello dell'acqua sopraraffreddata, è metastabile e la sua pressione è negativa; più precisamente si può dimostrare che vale la relazione −P = ρ_v, dove ρ_v è la densità di energia del vuoto, dovuta ai campi di Higgs. Quest'ultima vale approssimativamente

cioè la densità di energia corrispondente a una particella di Higgs di massa M nel volume di una sua lunghezza Compton. È facile capire qualitativamente come una pressione negativa cambi radicalmente la velocità di espansione dell'universo. Per vederlo usiamo la relazione

che segue dalle (8) e (9). Quando P > 0, la gravità produce un'accelerazione negativa e quindi una forza attrattiva. Quando invece ρ + 3P 〈 0, la forza gravitazionale diventa repulsiva e produce perciò un aumento dell'espansione. Inoltre, come discende dalla (9), una pressione negativa produce un aumento dell'energia con l'espansione e questo (v. È a) è condizione necessaria per la soluzione del problema dell'orizzonte.

Con l'equazione di stato P = − ρ_v = cost la soluzione delle (8) e (9) per

tende ad

dove

La crescita esponenziale (52) continua per un tempo Δt 10^-32 s dopodichè la fase instabile simmetrica sparisce (come l'acqua sopraraffreddata si trasforma rapidamente in ghiaccio) per dar luogo alla fase stabile asimmetrica. In questa transizione l'energia del vuoto ρ_v si converte in energia termica delle particelle originate dalla distruzione dei campi simmetrici (particelle di Higgs).

L'effetto dell'espansione esponenziale (52) è quello di produrre un enorme aumento dell'orizzonte. Per esempio, se a t₆ l'orizzonte era di qualche decina di migliaia di lunghezze d'onda di de Broglie, all'energia kT₆ ≃ 10²³ eV, cioè

h(t₆) ≃ 10^-24 cm

dopo un tempo Δt ~ 10^-32 s, l'orizzonte ha raggiunto il valore

h(t₆ + Δt) ≃ 10⁵⁰ × 10^-24 cm ≃ 10²⁶ cm

cioè è dell'ordine delle dimensioni dell'universo visibile. Quest'ultimo è dunque il prodotto di quella ‛bolla' di materia simmetrica sopraraffreddata.

Come si vede dalla fig. 3, che mostra l'andamento dell'orizzonte e del fattore di scala sia nel modello standard che in quello inflazionistico, il problema dell'orizzonte è completamente superato con l'ipotesi dell'espansione esponenziale. Anche il problema della curvatura è risolto: infatti l'universo attualmente osservabile rappresenta in questo modello una frazione piccolissima dell'intero universo e perciò la geometria appare euclidea nello stesso modo come una piccola porzione di superficie sferica appare piatta. In effetti il modello inflazionistico predice che il valore di Ω = ρ₀/ρ0_c debba essere, con enorme precisione, uguale a 1. La previsione non è facilmente verificabile data l'incertezza esistente sul contributo della massa oscura.

Secondo la teoria la fase di espansione esponenziale, durante la quale la temperatura scende esponenzialmente, cessa quando, nel passaggio alla fase asimmetrica, l'energia del vuoto si trasforma in energia termica delle particelle, con produzione di entropia, mentre la temperatura ritorna approssimativamente alla temperatura T₆ . Da quel punto in poi la temperatura decresce come nel modello standard. Anche la densità, che nella fase di espansione era restata costante, inizia a diminuire come t^-2, in accordo con il modello standard.

L'espansione esponenziale connessa alla transizione di fase nella quale si rompe la G-simmetria sembra dunque risolvere i problemi inerenti al modello standard, senza peraltro alterarne la validità, se non durante un tempo Δt ~ 10^-32 s intorno a 10^-35 s. Il modello inflazionistico fornisce anche una giustificazione dell'eccesso di nucleoni nel nostro universo. Infatti durante la fase di espansione esponenziale l'equilibrio termodinamico è rotto (la fase simmetrica è metastabile). Si realizza così una delle condizioni necessarie per la produzione di un eccesso di quarks rispetto agli antiquarks. Poiché le altre due condizioni (violazioni di B e di CP; v. cap. 6, È c) sono verificate nella teoria unificata, si raggiunge così una spiegazione dell'eccesso di nucleoni nell'universo attuale. Nella sua forma attuale la teoria non predice però il valore di n0_γ/n0_N.

Il modello inflazionistico semplificato che abbiamo esposto conduce ad alcune incongruenze, alcune delle quali sono state però recentemente eliminate usando una descrizione più precisa della transizione di fase (v. Linde, 1984). Osserviamo infine che sembra possibile che le inomogeneità create dalle fluttuazioni quantistiche dei campi di Higgs possano venire amplificate nell'espansione fino a raggiungere dimensioni astronomiche. Le fluttuazioni quantistiche potrebbero essere dunque i semi delle strutture attuali dell'universo, il che può essere considerato come una versione moderna delle antiche speculazioni sulle relazioni fra il microcosmo e il macrocosmo. In termini più precisi potremmo dire che questo sarebbe un esempio di come le leggi fondamentali della fisica determinino completamente la struttura interna dell'universo. È prudente tuttavia tener presente la natura altamente ipotetica delle speculazioni discusse in questo capitolo.

8. L'origine delle strutture dell'universo

a) La gravitazione come causa delle strutture.

In questo capitolo descriveremo brevemente come da un universo essenzialmente uniforme - quale esso era fino all'età di circa 10⁵ anni - abbiano potuto aver origine le strutture che oggi osserviamo: stelle, galassie, ammassi di galassie, superammassi, le cui masse vanno da 1 a 10¹⁵-10¹⁶ masse solari.

È opportuno però avvertire subito il lettore che il problema di spiegare l'origine di queste strutture e il loro spettro di massa è ben lungi dall'essere risolto. Nessuno dei vari modelli proposti è completamente soddisfacente e tutti devono fare appello a ipotesi la cui validità resta ancora da giustificare. Tutti i modelli poi soffrono della scarsità delle nostre conoscenze dei fenomeni collettivi in campi gravitazionali. Ci limiteremo quindi ad accennare a quegli aspetti che sembrano ragionevolmente ben stabiliti.

È innanzitutto evidente che per spiegare l'origine delle strutture che oggi osserviamo dobbiamo ammettere che nel plasma dominato dalla radiazione devono essere esistite delle fluttuazioni δρ e della densità di energia. L'ampiezza di tali fluttuazioni dev'essere stata sufficientemente grande da poter crescere fino a dar luogo alle strutture attuali. D'altra parte la loro ampiezza non dev'essere stata tanto grande da causare una inomogeneità della radiazione di fondo maggiore del limite superiore osservato (ΔT/T ≤ 10^-4). Infine le fluttuazioni devono essere state tali da non produrre inomogeneità con masse superiori a quelle dei superammassi (10¹⁵-10¹⁶ masse solari). Infatti alla scala di masse superiore a quella dei superammassi l'universo appare essenzialmente uniforme.

Il meccanismo capace di amplificare le fluttuazioni è chiaramente la gravitazione, il cui raggio d'azione, come del resto quello delle interazioni elettromagnetiche, è infinito. Tuttavia, nel plasma neutro esistente prima della formazione degli atomi, il raggio d'azione delle forze elettromagnetiche è limitato dall'azione di schermo delle cariche di segno opposto. Pertanto la gravitazione sembra essere l'unica forza capace di agire su grandi distanze.

Consideriamo un mezzo con densità di energia ρ, e supponiamo che in un certo volume la densità, per qualche ragione, aumenti di una quantità δρ. La maggiore energia (massa) contenuta in questo volume tende ad attrarre verso il volume in questione la massa circostante e quindi ad amplificare δρ. A questo aumento di δρ si oppone però l'aumento di pressione che accompagna l'aumento della densità di energia.

Si può dimostrare che le fluttuazioni su piccola scala, che coinvolgono quindi piccole masse, si propagano nel mezzo come onde sonore. Quelle su grande scala invece tendono ad amplificarsi, perché in questo caso l'effetto della gravità predomina su quello della pressione. La lunghezza d'onda che separa le perturbazioni che si propagano come onde sonore da quelle la cui ampiezza si amplifica è la cosiddetta lunghezza di Jeans λ_J = c_s (πc²/Gρ)^1/2, dove c_s, è la velocità del suono e ρ la densità di energia del mezzo.

Perché l'ampiezza possa crescere occorre anche che la viscosità del mezzo, dovuta alle interazioni fra le particelle, sia piccola. Inoltre è necessario che le particelle non siano relativistiche. Infatti, se le particelle si muovono alla velocità della luce, possono smorzare l'ampiezza della perturbazione nel tempo necessario a percorrere la distanza λ_J/r che separa i massimi e i minimi di densità.

È così evidente che le fluttuazioni di densità non possono crescere nel plasma relativistico e viscoso che precede

il tempo di disaccoppiamento t₁ ≃ 10⁶ anni. Dopo quel momento gli elettroni e i protoni si combinano per formare atomi neutri e la pressione e la viscosità diminuiscono rapidamente, così che la crescita delle perturbazioni procede indisturbata sotto l'effetto della gravitazione. Da quel momento in poi il contrasto di densità δρ/ρ aumenta circa come t^2/3.

b) Impossibilità della formazione delle strutture dal gas neutro di idrogeno ed elio.

Le considerazioni esposte nel paragrafo precedente sembrerebbero suggerire che il gas neutro di H e He⁴ a bassa temperatura e perciò non relativistico, praticamente disaccoppiato dalla MBR, il quale riempiva uniformemente l'universo quando questo aveva poco più di 200.000 anni, fosse l'ambiente adatto per la formazione di strutture.

Questa ipotesi, che fino a una decina di anni fa appariva la più naturale, è però oggi difficilmente sostenibile.

Infatti supponiamo che, subito prima del tempo di disaccoppiamento t₁ ~ 10⁶ anni, il contrasto di densità di protoni ed elettroni fosse δρ₁/ρ₁. Poiché prima di t₁ la radiazione elettromagnetica era accoppiata al plasma di protoni ed elettroni, anche la radiazione doveva presentare un uguale contrasto di densità e pertanto dovevano esservi fluttuazioni di temperatura δΤ₁/T₁ = δρ₁/ρ₁. Nell'intervallo di tempo che intercorre fra t₁ e l'epoca nella quale sappiamo che esistevano già dei quasar, tq ≃ 2•10⁹ anni, il contrasto di densità sarebbe cresciuto di circa un fattore (2 × 10⁴)^2/3 ~ 700. Per ottenere la densità osservata dei superammassi dovremmo perciò supporre che al tempo t₁ il contrasto di densità fosse δρ₁/ρ₁, se la densità attuale è ρ₀ ≃ 5 × 10^-30 g/cm³, o addirittura δρ₁/ρ₁ ~ 10^-2, se è ρ₀ ≃ 5 × 10^-11 g/cm³.

Poiché da ti in poi la radiazione è disaccoppiata dalla materia, la radiazione di fondo dovrebbe quindi presentare delle fiuttuazioni δΤ/Τ dello 0,1% o addiriuura dell'1%, in contrasto con il limite superiore osservato: δT/T ≤ 10^-4.

c) La materia oscura come origine delle strutture.

Se l'origine delle strutture non può essere attribuita alla materia visibile, è naturale cercarla in quella materia oscura la cui presenza sembra anche richiesta dalla dinamica delle galassie e degli ammassi di galassie (v. cap. 1). Se le considerazioni precedenti sono corrette si potrebbe addirittura sostenere che la presenza della struttura dell'universo sia la migliore dimostrazione dell'esistenza di questa materia oscura.

Supponiamo che accanto alle particelle fin qui considerate ve ne siano altre che per il momento chiameremo Particelle, di massa m, che supporremo interagiscano debolmente fra loro e con le particelle normali. Perché una perturbazione della densità delle Particelle possa crescere occorre (v. È a) che esse abbiano energie non relativistiche: questo avviene quando la loro temperatura T, che diminuisce per effetto dell'espansione, diviene tale che

Una inomogeneità della densità delle Particelle anche di notevole ampiezza non induce direttamente una inomogeneità apprezzabile nel plasma di elettroni, protoni e fotoni, poiché abbiamo ammesso che le Particelle abbiano con tale plasma un'interazione debolissima. Le fluttuazioni della loro densità possono iniziare a crescere prima di t₁ senza per questo indurre inomogeneità nel plasma di fotoni e di elettroni. Queste inomogeneità nella densità delle Particelle producono però dei pozzi di potenziale gravitazionale nei quali la materia normale, ma non i fotoni, verrà a cadere, dando così origine alle strutture visibili. Questo meccanismo consente dunque in linea di principio di ottenere delle strutture visibili senza indurre disomogeneità apprezzabili della MBR.

Naturalmente i dettagli quantitativi di questo modello e la natura delle strutture generate dipendono criticamente dalle proprietà delle Particelle e dal rapporto fra la loro densità e quella dei fotoni. Supponiamo, per esempio, che le Particelle siano neutrini elettronici dotati di una massa m = 30 eV (ammesso che questo valore della massa sia confermato). In questo caso conosciamo con precisione la loro densità numerica. I neutrini massicci diventarono non relativistici quando l'universo aveva circa 500 anni, cioè molto prima degli elettroni. Si può dimostrare che, in queste condizioni, ogni perturbazione di dimensioni lineari inferiori a una lunghezza che, riportata alla scala attuale dell'universo, corrisponderebbe a 5-10 Mpc verrebbe smorzata per effetto della diffusione dei neutrini relativistici. Le perturbazioni su una scala lineare maggiore possono invece crescere e dare origine a gigantesche condensazioni di neutrini. La regione in cui avviene la condensazione del gas neutro è determinata dalla distribuzione spaziale delle dense nuvole di neutrini. Le masse di gas neutro, scontrandosi fra loro, danno origine a onde d'urto che ionizzano nuovamente il gas e lo comprimono in sottili strati: questi sono instabili e possono frammentarsi in galassie.

La differenza tra il comportamento del gas e quello dei neutrini è dovuta alla perdita di energia per collisioni e per radiazione, che nel gas giocano un ruolo importante. Perdendo energia per radiazione, il gas si raffredda, rendendo così possibile la formazione delle stelle nelle galassie. Ciò spiega in maniera naturale l'esistenza dei vuoti, che sarebbero gli spazi compresi tra le regioni dove avviene la condensazione di galassie e stelle, spazi contenuti in un gas rarefatto ionizzato e scaldato dalla radiazione.

Il modello che abbiamo testé discusso si fonda sull'ipotesi, non ancora verificata, che i neutrini elettronici abbiano una massa diversa da zero. Se ciò non fosse, bisognerebbe supporre che la massa oscura sia fornita da qualcuna delle numerose particelle non ancora osservate, ma la cui esistenza è prevista dalle teorie supersimmetriche (fotini, gravitini, ecc.). Supponiamo che la densità numerica di queste Particelle sia 10³ volte inferiore a quella dei neutrini, ma che la loro massa di riposo sia 10³ volte maggiore di quella (ipotetica) dei neutrini, cioè poniamo m = 30 KeV. La densità di massa di queste Particelle sarebbe dunque uguale a quella usata nel modello con neutrini massicci. Tuttavia queste Particelle diventerebbero non relativistiche assai prima, cioè a una temperatùra maggiore: da quel momento in poi le perturbazioni di densità possono crescere, sebbene la crescita non diventi veramente importante fino a quando la massa oscura non divenga la componente dominante della densità totale. Come avviene per i neutrini, si formano per prime le perturbazioni di densità delle Particelle, dopodiché la materia normale si condensa nei pozzi di potenziale formati dalle Particelle.

La differenza rispetto al caso dei neutrini è dovuta al fatto che la scala caratteristica delle perturbazioni è mille volte minore, il che fa sì che come prima entità si formino le galassie. Contemporaneamente alle perturbazioni su scala ridotta sono presenti anche perturbazioni su scala più vasta, cosicché le galassie formate si riuniscono in seguito in ammassi di galassie.

In breve la differenza tra il modello che ipotizza neutrini massicci e quello che suppone l'esistenza di Particelle pesanti sta nel fatto che nel modello a neutrini nascono prima delle grandi nubi che si frazionano poi in varie galassie, mentre nel modello a Particelle pesanti si sarebbero prima formate delle galassie le quali in seguito si sarebbero riunite in ammassi.

d) Il ruolo delle esplosioni stellari.

I modelli esaminati nei paragrafi precedenti si basano tutti sull'ipotesi che le strutture attuali dell'universo siano state prodotte esclusivamente da instabilità gravitazionali. Non vi è alcun dubbio che questa sia la causa prima dell'inomogeneità del plasma uniforme che riempiva l'universo 200.000 anni dopo la sua nascita. È tuttavia possibile che la crescita delle perturbazioni risulti profondamente modificata se si tiene conto dell'energia nucleare liberata nelle stelle e in particolare nelle esplosioni delle supernove. Una tale possibilità è suggerita dalle osservazioni fatte nella nostra galassia, le quali mostrano che le onde d'urto prodotte dalle esplosioni stellari hanno una parte molto importante nel riscaldamento e nella ionizzazione del mezzo interstellare, tantoché l'esplosione di una supernova può innescare nel gas interstellare il processo di formazione di stelle.

Occorre ricordare che le stelle la cui massa è compresa tra dieci e cento volte quella del Sole' hanno un'evoluzione assai rapida, ossia vivono meno di un milione di anni dalla nascita alla morte esplosiva, un tempo assai breve rispetto a quelli che ci interessano. Si può così pensare a una sequenza di esplosioni consecutive, cioè a un processo simile alla detonazione di un esplosivo: la reazione che avviene in uno strato innesca le reazioni nello strato adiacente e così via. Osserviamo che tale meccanismo è ancor più efficace se il mezzo in cui si propaga l'onda di detonazione è inomogeneo, e che la velocità di propagazione aumenta con la rarefazione del gas.

Per comprendere come un meccanismo del genere possa determinare la formazione delle galassie, bisogna ammettere che inizialmente una piccola quantità di materia si condensi in galassie per effetto di instabilità gravitazionali. Saranno poi le onde d'urto generate dalle esplosioni stellari che avvengono nelle poche galassie così formate ad amplificare, nella restante parte del gas, le piccole perturbazioni di densità esistenti e quindi a permettere la formazione di altre galassie.

È possibile che questo modello permetta di eliminare la contraddizione fra l'ampiezza delle fluttuazioni di densità richiesta per la formazione delle galassie dal gas di H, He⁴ e fotoni e il limite posto dalle osservazioni sull'ampiezza delle fluttuazioni δΤ/Τ della MBR. Era proprio questa contraddizione (v. È b) che aveva suggerito di cercare nelle fiuttuazioni della massa oscura l'origine delle galassie.

Molto resta ancora da fare prima di poter avere una teoria soddisfacente della formazione delle galassie. Da un lato le nostre conoscenze sulla fisica delle particelle elementari non sono sufficienti a permetterci di sapere quale fosse esattamente la composizione dell'universo all'epoca in cui la formazione delle galassie è cominciata. Dall'altro non possiamo escludere che l'origine di queste strutture vada ricercata in meccanismi per così dire ‛ibridi', che tengano conto sia delle interazioni gravitazionali sia di quelle nucleari attraverso esplosioni multiple di supernove. Non è irragionevole sperare che nel prossimo futuro dallo studio delle proprietà delle galassie e degli altri oggetti dell'universo e dalle ricerche sulla fisica delle altissime energie possa scaturire una teoria soddisfacente dell'origine della struttura attuale dell'universo.

Vogliamo infine accennare al fatto che secondo altre teorie l'origine delle strutture va attribuita a fluttuazioni del rapporto fra il numero dei nucleoni e quello dei fotoni, cioè a fluttuazioni di entropia. Secondo queste teorie le prime a formarsi sarebbero state condensazioni con masse dell'ordine di 10⁵-10⁶ masse solari, dalle quali avrebbero poi avuto origine le strutture maggiori. (Per una trattazione dettagliata dei vari modelli v. Zeldovich e Novikov, 1983). Da ultimo osserviamo che il modello inflazionistico suggerisce altri meccanismi per la crescita delle fluttuazioni, che cambierebbero notevolmente la storia dell'evoluzione delle grandi strutture.

9. Conclusioni

Qual è il grado di attendibilità del modello di universo che abbiamo tratteggiato nelle pagine precedenti? Per valutarlo conviene anzitutto tenere presente l'imprecisione di alcuni dati osservativi su cui il modello si basa: il valore della costante di Hubble, la densità media della materia, la percentuale di materia oscura e la sua natura, e la genealogia delle galassie sono ancora mal noti.

Similmente manchiamo di alcuni dati importanti sui costituenti microscopici dell'universo, quali i valori delle masse dei neutrini, il numero delle loro specie - per ora se ne conoscono tre, ma nulla ci assicura che non ne possano esistere altre - e la vita media del protone, dato quest'ultimo importante per la conferma della possibilità della produzione spontanea del numero barionico attuale dell'universo.

A questa carenza di conoscenze empiriche si aggiunge la mancanza di uno schema teorico sicuro, almeno per quanto riguarda le fasi iniziali dello sviluppo dell'universo. E poiché quello che è avvenuto all'inizio, o per lo meno dopo la fine dell'espansione esponenziale, ha in qualche modo determinato lo sviluppo successivo, dobbiamo tener presente la possibilità che nuove e più sicure teorie possano alterare, anche profondamente, l'immagine che oggi ci facciamo dell'universo. Del resto non va dimenticato che anche nei campi più classici, dove le equazioni sono ben stabilite, la nostra conoscenza degli effetti collettivi non lineari è ancora assai rudimentale. Tali effetti, i quali, come da poco sappiamo, sono responsabili della formazione delle strutture su piccola scala, giocano probabilmente un ruolo egualmente importante su scala astronomica. Va in particolare sottolineato il fatto che persino la dinamica e l'evoluzione dei sistemi stellari (galassie) sono ancora mal note e che i recenti progressi compiuti in questo campo hanno messo in luce l'importanza determinante dei fenomeni collettivi.

Se le incertezze che abbiamo testé ricordato ci devono indurre a un sano scetticismo - il quale del resto è una delle doti essenziali dello scienziato -, non dobbiamo dimenticare che il modello dell'universo che abbiamo presentato ha condotto alla spiegazione di dati osservativi ben stabiliti: la recessione delle galassie, l'origine e l'omogeneità della radiazione di fondo, il rapporto fra le abbondanze di idrogeno e di elio e, attraverso i processi che avvengono nelle stelle, degli elementi più pesanti. Inoltre il modello fornisce una spiegazione, sia pure per ora soltanto qualitativa, dell'origine dell'eccesso di nucleoni e, nella sua versione più recente (modello espansionistico), permette di superare le difficoltà dei modelli precedenti (problemi dell'orizzonte e della curvatura).

Prima di concludere questo articolo vogliamo accennare ad alcuni problemi di carattere più speculativo. Il primo riguarda il cosiddetto ‛termine cosmologico', che, come abbiamo avvertito nel cap. 4, può essere aggiunto nelle equazioni di Einstein. Attualmente sappiamo che tale termine, il quale rappresenta la curvatura del vuoto, deve essere estremamente piccolo: esso, in linea di principio, può essere calcolato, pur di possedere una teoria di campo precisa, valida fino ai primissimi istanti dell'universo. In assenza di una tale teoria nulla di molto preciso si può concludere sul termine cosmologico.

Il secondo problema riguarda l'origine dell'universo. Secondo alcune recenti speculazioni esso potrebbe essere apparso dal nulla. La ragione per una tale affermazione - il cui significato è peraltro poco chiaro - si basa sul fatto che, secondo le idee attuali, l'universo può avere le caratteristiche che ha provenendo, senza violare alcuna legge di conservazione, da uno stato - il nulla - con carica elettrica, numero barionico ed energia nulli. Infatti la carica elettrica totale dell'universo è nulla; il suo numero barionico B ≠ O può, secondo le teorie attuali (v. cap. 6), essere stato prodotto per rottura spontanea della simmetria per lo scambio di particelle e antiparticelle; infine (v. cap. 4), l'energia totale - cioè la somma di quella della materia e di quella della radiazione - può essere zero. L'energia non gravitazionale attuale - la quale, da sola, non è conservata - può avere avuto origine, a spese dell'energia del vuoto, nella fase inflazionistica.

Il terzo e ultimo problema riguarda il futuro dell'universo. Come abbiamo visto nel cap. 4 l'espansione può continuare indefinitamente o cessare per poi invertirsi, a seconda del valore del rapporto fra la densità di energia e la densità critica. Poiché tale valore è mal conosciuto, non si può fare alcun pronostico sicuro sul futuro dell'universo. Possiamo solo speculare sullo stato dell'universo nel caso l'espansione continui per un tempo sufficientemente lungo: a causa della non conservazione del numero barionico, tutti i nucleoni attuali dovrebbero scomparire, trasformandosi in elettroni, positroni, neutrini e fotoni. Un universo etereo e inospitale.

Bibliografia

Einstein, A., Die Grundlage der allgemeinen Relativitätstheorie, in ‟Annalen der Physik", 1916, XLIX, pp. 769-882.

Friedmann, A., Über die Krümmung des Raumes, in ‟Zeitschrift für Physik", 1922, X, pp. 377-386.

Friedmann, A., Über die Möglichkeit einer Welt mit konstanter negativer Krümmung des Raumes, in ‟Zeitschrift für Physik", 1924, XXI, pp. 326-332.

Gamow, G., Expanding universe and the origin of elements, in ‟Physical review", 1946, LXX, pp. 572-573.

Gamow, G., The origin of elements and the separation of galaxies, in ‟Physical review", 1948, LXXIV, pp. 505-506.

Georgi, H. M., Glashow, S.L., Unity of all elementary-particle forces, in ‟Physical review lettees", 1974, XXXII, pp. 438-441.

Guth, A., Inflationary universe: a possible solution to the horizon and the flatness problems, in ‟Physical review", 1981, XXIII (D), pp. 347-356.

Hove, L. van, Non equilibrium processes in early cosmology, TH 3623-CERN, Genève 1984.

Hubble, E., A relation between distance and radial velocity among extragalactic nebulae, in ‟Proceedings of the National Academy of Sciences", 1929, XV, pp. 168-173.

Kazanas, D., Dynamics of the universe and spontaneous symmetry breaking, in ‟Astrophysical journal", 1980, CCXLI, pp. L59-63.

Lemaître, G., Un univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radicale des nébuleuses extra-galactiques, in ‟Annales de la Société Scientifique de Bruxelles", 1927, XLVII (A), pp. 49-59.

Linde, A.D., The inflationary univesre, in ‟Report on progress in physics", 1984, XLVII, pp. 925-986.

Partridge, R.B., The cosmic microwave background at its twentieth anniversary, in Twelfth Texas symposium on relativistic astrophysics, New York 1986.

Penzias, A.A., Wilson, R.W., A measurement of excess antenna temperature at 4080 Mc/s, in ‟Astrphysical journal", 1965, CXLII, pp. 419-421.

Sacharov, A.D., Violation of CP invariance, C asymmetry and baryon asymmetry of the univesre, in ‟Pis'ma. Zurnal eksperimental'noj i teoreticeskoj fiziki", 1967, V, pp. 32-35 (tr. ingl. in ‟JEPT letters", 1967, V,pp. 24-27).

Salam, A., Weak and electromagnetic interactions, in Proceedings of the Nobel symposium n. 8 (a cura di N. Svartholm), New York 1969, pp. 367-377.

Weinberg, S., A model of leptons, in ‟Physical review letters", 1967, XIX, pp. 1264-1266.

Weinberg, s., The first three minutes, New York 1977 (tr. it.: I primi tre minuti, Milano 1977).

Zeldovich, Ja. B., Novikov, I.D., The structure and evolution of the universe, Chicago 1983.