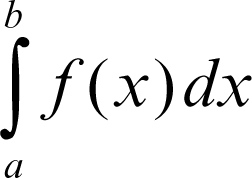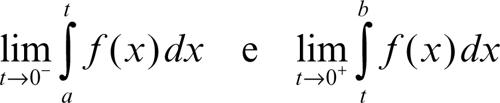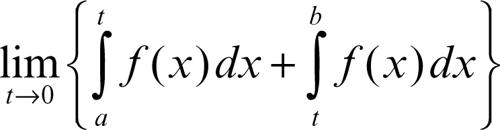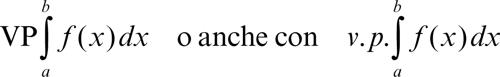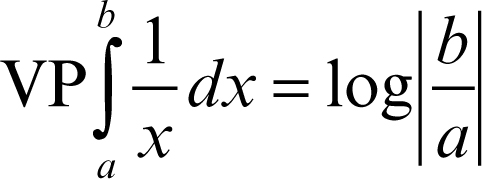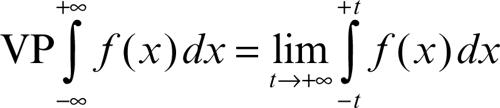valore principale

valore principale

valore principale in analisi, locuzione utilizzata per un integrale (→ integrale, valore principale di Cauchy di un), per una serie bilatera o, più in generale, per un limite doppio, qualora le due variabili tendano al rispettivo punto di accumulazione legate tra loro in modo particolarmente simmetrico. Per esempio, se una funzione ƒ(x) è discontinua nell’origine, l’integrale improprio (essendo ƒ discontinua in 0)

con a < 0 < b, è definito come somma dei due limiti, rispettivamente sinistro e destro

Questi possono non convergere separatamente, ma può esistere il

nel quale è stato tolto un intorno simmetrico dell’origine, la cui lunghezza si fa tendere a 0: se ciò avviene, il valore ottenuto si chiama valore principale dell’integrale dato e si indica con

Per esempio, la funzione ƒ(x) = 1/x non è integrabile in un intorno dell’origine, ma essendo una funzione dispari si trova il

(in particolare, se a = −b, l’integrale vale 0).

Analogamente si definiscono

e anche

Questo tipo di integrali si trova frequentemente nel calcolo di integrali mediante il metodo dei residui (→ residuo) e nella teoria delle → distribuzioni.