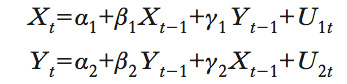VAR
VAR
Modello autoregressivo vettoriale che estende l’autoregressione univariata (➔ autoregressivo, modello) a serie storiche multiple, cioè a un vettore (➔) di serie storiche (➔). Un VAR con due variabili, Xt e Yt, consiste di due equazioni. Nella prima la variabile dipendente è Xt, nella seconda è Yt. I regressori di entrambe le equazioni sono i valori ritardati delle due variabili del modello. Quando il numero di ritardi, in entrambe le equazioni, è uguale a p, si dice che il modello è di ordine p e si indica con VAR(p). Il modello a due equazioni di ordine 1 si scrive:
dove i βi e i γi sono i coefficienti ignoti e gli Ui sono i termini di errore. Sotto opportune assunzioni, simili a quelle richieste da un modello autoregressivo, i coefficienti del VAR possono essere stimati in maniera consistente applicando il metodo dei minimi quadrati ordinari (➔ minimi quadrati, metodo dei) a ogni equazione. La distribuzione delle stime così ottenute è approssimata da una distribuzione normale (➔ gaussiana, distribuzione). La scelta del numero p di ritardi da includere è uno degli aspetti cruciali nella specificazione di un VAR. Un numero elevato di ritardi determina un numero molto grande di coefficienti da stimare e può causare una forte diminuzione dell’accuratezza delle stime e un aumento sostanziale dell’errore di previsione. Per es., se le equazioni sono 5 e si includono 3 ritardi per ciascuna variabile, si ottengono ben 80 coefficienti da stimare, che si riducono a 55 se i ritardi sono soltanto due. Per la scelta del numero di ritardi da includere nel VAR, si possono usare metodi di selezione del modello basati, per es., sul test F (➔ F, test) o su criteri di informazione (➔ selezione di un modello). Anche la scelta del numero di variabili da mettere in relazione in un modello autoregressivo vettoriale è importante: introdurre una variabile che non è in relazione con le altre accresce l’errore della stima senza migliorare la capacità predittiva. ● I modelli VAR sono stati introdotti nel 1980 da C.A. Sims (➔) allo scopo di esplorare le relazioni causali tra variabili economiche (➔ causalità). Tali modelli prendono il nome di VAR strutturali quando sono usati per modellare la struttura del fenomeno economico che si vuole indagare.