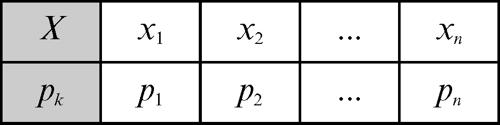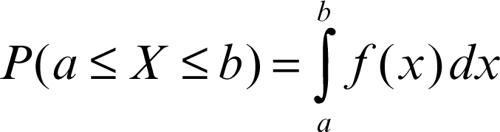variabile aleatoria

variabile aleatoria

variabile aleatoria o variabile casuale o variabile stocastica, in probabilità, funzione reale X: Ω → R, dove Ω è uno → spazio degli eventi. Se Ω è discreto, la variabile aleatoria si dice discreta, altrimenti si dice continua. A una variabile aleatoria discreta è associata una funzione di probabilità (→ distribuzione di probabilità, funzione di); a una variabile aleatoria continua è associata una funzione di densità di probabilità (→ densità, funzione di). A ogni possibile esito di un esperimento casuale (evento E ⊆ Ω) è così associato un numero reale X(E) = x ∈ R e si indicano con (X = a), (X ≤ b), (X ∈ I), ..., rispettivamente, gli eventi «X assume il valore a», «X assume valori minori o uguali a b», «X cade nell’intervallo I». Se di ogni evento E si conosce la probabilità, si conosce allora la legge di distribuzione di probabilità che associa a ogni intervallo I ⊆ R la probabilità che X assuma un valore reale appartenente a I. Una variabile aleatoria è strettamente connessa alla sua distribuzione di probabilità e perciò i diversi tipi di variabile aleatoria teorica (normale, binomiale, geometrica ecc.) sono spesso classificati in relazione alle loro distribuzioni (si veda → distribuzione normale; → distribuzione binomiale; → distribuzione geometrica ecc.).

Variabile aleatoria discreta

Nel caso di variabile aleatoria finita (e quindi necessariamente discreta), se x₁, ..., x_n sono i valori che essa può casualmente assumere, si ha P(X = x) = 0, se x ≠ x_k per ogni k = 1, ..., n, e P(X = x) = p_k (con 0 ≤ p_k ≤ 1) se x = x_k per qualche k = 1, ..., n. In queste scritture, P(X = x) è da leggersi come «probabilità che X assuma il valore x» mentre p_k è il numero reale che esprime la probabilità che sia X = x_k. È da notare che deve essere

formula che facilmente si estende al caso di variabile aleatoria discreta con infiniti valori.

Di fatto, una variabile aleatoria finita è assegnata quando è data una tabella del tipo

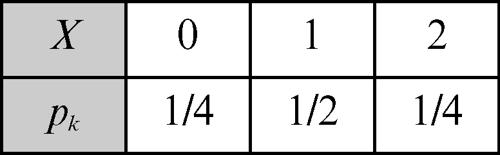
Per esempio, considerato lo spazio di eventi associato all’esperimento del lancio di due monete, i cui eventi elementari sono TT, TC, CT, CC, si può allora definire la variabile aleatoria X = «numero di croci uscite» così assegnata in tabella

Definire una variabile aleatoria significa quindi assegnare una regola in base alla quale si associa un numero reale a ogni risultato di un esperimento e quindi a ogni elemento dello spazio campionario Ω; in corrispondenza, se ne assegna un valore di probabilità.

Tipico dei giochi di azzardo è il procedimento di assegnazione di premi o pagamenti associati a eventi casuali e ciò definisce appunto una variabile aleatoria. Per esempio, nel gioco della roulette si punta una somma S sull’uscita, sulla ruota, di un numero k tra i possibili 37 numeri (da 0 a 36). Se esce il numero k su cui si è puntato, si riceve una somma pari a 36 volte la posta (si guadagna cioè una somma uguale a 35S); altrimenti, si perde S, cioè quanto scommesso. È così definita la variabile aleatoria

dove i valori −S e +35S sono rispettivamente associati all’uscita di un numero diverso da quello sul quale si è puntato oppure al numero k su cui si è puntato.

Variabile aleatoria continua

Una variabile aleatoria continua si definisce in modo analogo al caso discreto, salvo il fatto che qualunque valore di probabilità puntuale, P(X = a), è uguale a zero. Se il dominio di riferimento Ω è infatti continuo, la probabilità di ricadere in un punto, cioè la misura di tale regione, è nulla. Così, per esempio, va considerata uguale a zero la probabilità di fare esattamente centro in un bersaglio circolare, mentre può essere assegnata una adeguata distribuzione di probabilità (e quindi definita una appropriata variabile aleatoria continua) a una catalogazione di eventi che indichi opportune corone circolari, di vario raggio, attorno al centro stesso.

A una variabile aleatoria continua X è quindi associata una funzione di densità ƒ(x) che esprime come la probabilità si addensa intorno al valore x. La funzione di densità è tale che ƒ(x) ≥ 0 per ogni x e inoltre

La probabilità che tale variabile aleatoria assuma valori nell’intervallo I è data da:

In generale, un variabile aleatoria X è continua se esiste una funzione ƒ(x) tale che:

dove a e b sono numeri reali tali che a ≤ b. I parametri che sintetizzano le caratteristiche di una variabile aleatoria sono la sua media (→ variabile aleatoria, valore medio di una) e la sua → varianza.

Variabile aleatoria multivariata

Generalizzazione della variabile aleatoria: la variabile (X₁, ..., X_n) associa a ogni evento E dello spazio degli eventi Ω una n-pla ordinata (x₁, ..., x_n) ∈ Rⁿ di valori reali. Come nel caso unidimensionale, tale variabile può essere discreta o continua. In particolare, se n = 2 si parla di variabile aleatoria doppia o bivariata (alcuni autori riservano quest’ultimo aggettivo soltanto alle variabili aleatorie doppie discrete). Per le variabili aleatorie doppie e, più in generale, multivariate, si possono considerare le variabili aleatorie marginali, relative alle singole variabili che le compongono, insieme con le corrispondenti funzioni marginali di probabilità (si veda → distribuzione di probabilità, funzione di). Nel caso di variabile aleatoria doppia (X, Y), si può costruire una tabella a doppia entrata, che rappresenta le probabilità relative a tutte le possibili coppie di valori delle singole modalità che possono essere assunte da X e Y. In questo caso, la probabilità che la variabile X assuma il valore x_k e la variabile Y assuma il valore y_h è indicato con p(x_k, y_h) = P(X = x_k, Y = y_h).

Il valore marginale p(y_h) è uguale alla somma di tutti i valori di probabilità della colonna della tabella a doppia entrata intestata y_h. Per ogni h si ha

In modo analogo si ottiene la funzione marginale della variabile X, per ogni k:

Gli insiemi di valori P(X) = {p(x_1.), p(x_2.), ..., p(x_n.)} e P(Y) = {p(y_.1), p(y_.2), ..., p(y_.n)}, posti rispettivamente nell’ultima riga e nell’ultima colonna della tabella, sono le distribuzioni marginali di probabilità relative rispettivamente alla sola variabile X e alla sola variabile Y.

Nel caso di variabili aleatorie doppie o multivariate si pone il problema di analizzare se le loro singole componenti sono o meno indipendenti: tale analisi è detta analisi bivariata o multivariata e si avvale di strumenti di indagine quali il → chi-quadrato o gli indici di → correlazione.