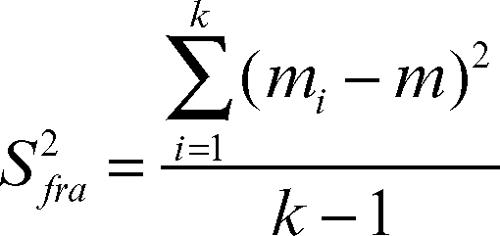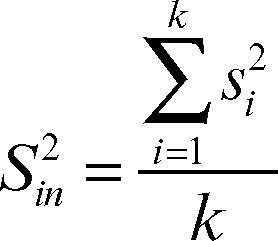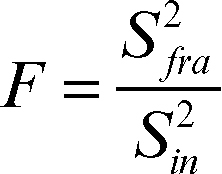varianza

varianza

varianza in statistica, indice di dispersione, indicato con σ² (si legga: «sigma quadro»), di un insieme di dati statistici e, quindi, della distribuzione di una variabile statistica o aleatoria. È espressa dalla media dei quadrati degli scarti dei valori osservati di una popolazione dalla loro media aritmetica

dove x_i sono le n osservazioni effettuate e x̄ è la loro media aritmetica. La varianza di una variabile aleatoria X è anche indicata con Var(X) ed è calcolabile in modo più semplice come momento di ordine 2 della variabile aleatoria X − E(X) associata a X, attraverso la formula Var(X) = E(X ²) − [E(X)]², dove E(X ²) è il valore medio del quadrato della variabile X e [E(X)]² è il quadrato del valore medio di X. Come indice di variabilità, lo → scarto quadratico medio, di cui la varianza è il quadrato, è preferito alla varianza perché ha la stessa unità di misura dei dati.

Se k è una costante reale, per ogni variabile aleatoria X valgono le seguenti proprietà della varianza:

• Var(kX) = k ²Var(X)

• Var(k + X) = Var(X)

Due variabili aleatorie X e Y sono indipendenti se e solo se Var(X + Y) = Var(X) + Var(Y). La varianza è anche impiegata nell’analisi congiunta di più fenomeni affinché se ne possano metterne in evidenza le eventuali relazioni (si veda oltre).

Analisi della varianza

Procedura statistica per la verifica dell’ipotesi di uguaglianza fra le medie di k ≥ 2 campioni. La verifica si realizza ponendo a confronto la varianza campionaria delle medie di ciascun campione intorno alla media generale (varianza fra gruppi o spiegata, detta anche varianza between) con la varianza campionaria delle osservazioni intorno alla media del campione di appartenenza (varianza nei gruppi o residua, detta anche varianza within). Il fenomeno statistico di cui si vuole spiegare la variabilità in base a una o più → variabili categoriali è definito come variabile dipendente (o variabile risposta) e deve essere necessariamente rappresentato da una variabile statistica quantitativa continua. Le variabili statistiche indipendenti, che stabiliscono una ripartizione della variabile risposta in classi o strati, sono anche dette fattori e devono essere variabili categoriali o continue.

L’analisi della varianza, spesso indicata con l’acronimo inglese anova (analysis of variance) assume nomi diversi a seconda del numero delle variabili dipendenti o indipendenti:

• anova (one way o univariata) quando si ha una sola variabile dipendente e una sola variabile indipendente;

• anova fattoriale, quando si ha una sola variabile dipendente e più variabili indipendenti (o fattori);

• manova (multivariate analysis of variance) o anova multivariata, quando si hanno più di una variabile dipendente e più di una variabile indipendente.

Nell’anova univariata si suppone che k campioni indipendenti di uguale numerosità n provengano da popolazioni distribuite normalmente con medie μ_i (con i = 1, ..., k) e varianza σ². Si vuole verificare l’ipotesi nulla H₀: μ₁ = ... = μ_k contro l’ipotesi alternativa che almeno due medie siano diverse. Indicate con m_i le medie dei singoli campioni, con m la loro media e con s_i² le varianze dei singoli campioni, la varianza fra gruppi è data da

mentre la varianza nei gruppi è

Il test statistico utilizzato per l’anova è

che, se l’ipotesi nulla è vera, si distribuisce secondo la distribuzione F di Fisher con k − 1 e k(n − 1) gradi di libertà, rispettivamente al numeratore e al denominatore (→ Fisher, distribuzione F di). A un livello di significatività α, si confronta il valore sperimentale F ottenuto con il valore critico F_k−1, _{k(n−1), α} letto sulla tavola della distribuzione F di Fisher. Se F > F_k−1, k(n−1), α la differenza tra almeno due delle medie non è casuale e si rifiuta pertanto l’ipotesi nulla.