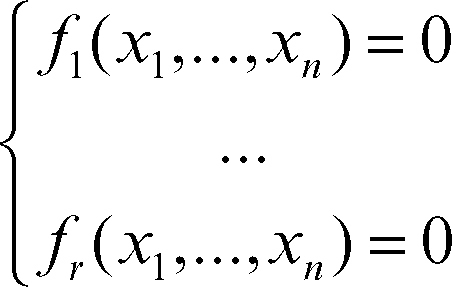varieta algebrica

varieta algebrica

varietà algebrica (in inglese algebraic variety o semplicemente variety) oggetto fondamentale in geometria algebrica che nasce dallo studio, da un punto di vista geometrico, dell’insieme delle soluzioni di un sistema di equazioni algebriche, cioè espresse mediante polinomi. Le varietà algebriche si suddividono in varietà affini e varietà proiettive.

Varietà affini

Una varietà affine su un campo K è un → insieme algebrico Z contenuto nello spazio affine Aⁿ =Aⁿ(K) che sia irriducibile come spazio topologico rispetto alla topologia di → Zariski indotta: ciò vuol dire che non esistono due chiusi Z₁ e Z₂ contenuti strettamente in Z tali che Z = Z₁ ∪ Z₂. È pertanto un insieme V di punti di uno spazio affine Aⁿ(K), dove K è un campo algebricamente chiuso, le cui coordinate soddisfano un sistema di equazioni algebriche.

A una varietà affine Z resta naturalmente associato l’ideale primo I ⊆ K [x₁, ..., x_n] formato dai polinomi che si annullano identicamente su Z. Se I è un ideale principale, cioè generato da un solo polinomio, allora Z prende il nome di ipersuperficie; in particolare se n = 2 si ha una curva algebrica piana, mentre se n = 3 si ha una superficie algebrica. Per esempio, è una varietà affine su R e una curva algebrica piana la circonferenza di centro l’origine e raggio 1 (insieme degli zeri del polinomio x ² + y ² = 1), e lo sono, più in generale, tutte le coniche, che possono essere descritte come il luogo degli zeri di un polinomio di secondo grado in due variabili. Una funzione regolare di Z è una funzione ovunque definita ƒ: Z → K esprimibile mediante un polinomio. L’insieme K [Z] delle funzioni regolari su Z costituisce un dominio d’integrità, detto anello delle coordinate di Z, il quale si identifica con l’anello quoziente K [x₁, ..., x_n] /I; il campo dei quozienti K(Z) di tale dominio d’integrità è detto campo delle funzioni razionali di Z. Proprietà algebriche dell’anello delle coordinate K [Z] rispecchiano proprietà geometriche della varietà affine Z e viceversa.

Se Z ∈ Aⁿ è una varietà affine e se p è un punto di essa, sia R_p ⊆ K(Z) l’anello dei → germi di funzioni regolari di Z definite in p e a valori nel campo K. Tale anello costituisce allora un anello locale (→ anello), il cui ideale massimale m_p coincide con l’insieme dei germi di funzioni che si annullano in p. Poiché K è contenuto in R_p (esso si identifica con l’insieme delle funzioni costanti), l’ideale m_p è in particolare uno spazio vettoriale su k; esso inoltre contiene come sottospazio vettoriale il suo quadrato m_p². Si definisce allora lo spazio tangente (di Zariski) (indicato con il simbolo T_pZ) di Z in p come lo spazio vettoriale (su k) duale dello spazio vettoriale quoziente m_p/m_p²:

(l’asterisco indica lo spazio duale). La dimensione di tale spazio vettoriale è costante su un aperto di Z: tale valore costante è detto dimensione di Z. In alcuni punti tuttavia la dimensione dello spazio tangente può essere superiore alla dimensione della varietà: un tale punto è detto punto singolare.

Per una definizione più formale, si consideri un campo K algebricamente chiuso e sia K [x₁, ..., x_n] l’anello dei polinomi a coefficienti in K. Sia inoltre Aⁿ = Kⁿ lo spazio affine n-dimensionale su K, dotato della topologia, detta topologia di → Zariski, nella quale i chiusi sono i sottoinsiemi algebrici di Aⁿ, costituiti dai punti le cui coordinate (x₁, ..., x_n) annullano una famiglia finita di polinomi

vale a dire dai punti che risolvono il sistema di equazioni algebriche

Poiché K [x₁, ..., x_n] è un anello noetheriano (→ anello; teorema della base di → Hilbert), i chiusi in tale topologia sono tutti e soli gli insiemi della forma V_A(I) = {x ∈ Aⁿ : ƒ(x) = 0, ∀ƒ ∈ I}, dove I è un arbitrario ideale di K [x₁, ..., x_n]. Se U_ƒ = Aⁿ − V_A(ƒ ), dove ƒ ∈ K [x₁, ..., x_n] è un polinomio, allora gli insiemi di tale forma costituiscono una base degli aperti della topologia di Zariski. Una varietà (algebrica) affine è allora un chiuso di Aⁿ rispetto a tale topologia; mentre una varietà quasi affine è un aperto di una varietà affine, relativamente alla topologia di Zariski su di essa indotta da Aⁿ.

Se K è un campo algebricamente chiuso (motivo per cui solitamente si assume che tale sia il campo di definizione di una varietà algebrica) è possibile stabilire una corrispondenza biunivoca fondamentale tra i chiusi algebrici di Aⁿ e una particolare classe di ideali di K [x₁, ..., x_n]. A ogni ideale I di K [x₁, ..., x_n] è infatti associata la varietà affine V_A(I) ∈ Aⁿ; tale corrispondenza può essere invertita associando a ogni varietà affine Z ∈ Aⁿ l’ideale ℑ(Z) di K [x₁, ..., x_n] costituito dai polinomi che si annullano su Z. Mentre però V_A(ℑ(Z)) = Z, è falso il viceversa: ℑ(V_A(I)) coincide infatti con Rad(I), l’ideale → radicale di I (teorema degli zeri di Hilbert). D’altra parte V_A(I) = V_A(Rad(I)), pertanto se ci si restringe a considerare gli ideali radicali di K[x₁, ..., x_n] si ottiene una corrispondenza biunivoca tra ideali radicali e chiusi algebrici di Aⁿ.

Varietà proiettive

Similmente al caso affine si possono considerare insiemi definiti algebricamente nello → spazio proiettivo Pⁿ = P(Kⁿ⁺¹): si definisce in questo caso la topologia di Zariski come la topologia nella quale i chiusi sono gli insiemi costituiti dai punti le cui coordinate omogenee (x₀, x₁, ..., x_n) annullano una famiglia finita di polinomi omogenei {ƒ₁, ..., ƒ_r} ∈ K [x₀, x₁, ..., x_n]. Così, se r = 1, si ha una curva algebrica piana per n = 2, una superficie algebrica per n = 3. Più in generale, i chiusi dello spazio proiettivo nella topologia di Zariski sono tutti e soli gli insiemi della forma V_P(I), dove I ∈ K [x₀, x₁, ..., x_n] è un ideale omogeneo (vale a dire generato da polinomi omogenei) diverso dall’ideale (x₀, x₁, ..., x_n). Una varietà (algebrica) proiettiva è un chiuso di P ⁿ rispetto a tale topologia; una varietà quasi proiettiva è un aperto di una varietà proiettiva, relativamente alla topologia di Zariski su di essa indotta da P ⁿ.

Se V_P(I) è una varietà proiettiva, allora le due ipotesi formulate sull’ideale I assicurano che, se π: Aⁿ⁺¹ − {0} → P ⁿ è la proiezione al quoziente e se V_A(I) ∈ Aⁿ⁺¹ è il chiuso affine associato a I, allora la varietà affine V_A(I) non è ridotta alla sola origine e, contenendo un punto x, contiene tutta la retta passante per x e per l’origine. Pertanto la varietà proiettiva V_P(I) coincide con l’immagine di V_A(I) tramite π; viceversa V_A(I) = π⁻¹(V_P(I)) ∩ {0}. Se Z è una varietà algebrica proiettiva, allora la varietà algebrica affine π⁻¹(Z) ∩ {0} è detta il cono affine sopra Z. Ogni varietà proiettiva può essere ricoperta da un numero finito di varietà affini, vale a dire le intersezioni della varietà stessa con i complementari degli iperpiani coordinati di P ⁿ definiti dall’equazione {x_i = 0}, dove i varia tra 0 e n. Pertanto le definizioni di spazio tangente e di punto singolare (che tengono conto solamente del comportamento locale della varietà) possono essere estese al caso di una varietà proiettiva; anche la nozione di dimensione di una varietà affine può essere estesa al caso di una varietà proiettiva.

Applicazioni tra varietà

Un’applicazione regolare (o polinomiale) ƒ: X → Y tra due varietà algebriche (affini o proiettive) X e Y è un’applicazione le cui coordinate sono espresse da polinomi, un’applicazione biregolare è un’applicazione regolare con inversa regolare. Un’applicazione razionale tra due varietà algebriche connesse è un’applicazione che sia regolare su un aperto non vuoto di X, ma possibilmente ovunque non definita; un’applicazione birazionale è un’applicazione che sia razionale con inversa razionale. La geometria algebrica studia in generale le proprietà legate alle applicazioni birazionali.

La nozione di varietà algebrica si generalizza successivamente in quella di schema, la quale, assieme allo spazio topologico X, assegna gli anelli delle funzioni regolari sui suoi aperti (il cosiddetto fascio strutturale dello schema), in modo che l’anello dei germi di funzioni regolari in un qualsiasi punto di X sia un anello locale; si richiede inoltre che, localmente, uno schema abbia la struttura topologica dello spettro di un anello commutativo unitario (→ anello), dotato della topologia di Zariski.