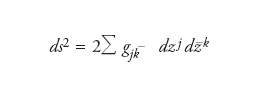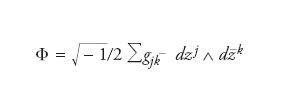varieta kahleriana

varietà kähleriana

Una metrica riemanniana su una varietà complessa M è detta hermitiana se definisce un prodotto interno hermitiano su ciascuno spazio tangente. Una metrica hermitiana si può esprimere nella forma

dove (g_jk^_) è una matrice n×n hermiti ana definita positiva che dipende da z¹,...,zⁿ. La connessione di Levi-Civita di M (vista come varietà riemanniana) può conservare, opppure non conservare, la struttura complessa di M; quando la conserva, la metrica hermitiana ds² è detta metrica di Kähler. Associamo alla metrica hermitiana una forma differenziale esterna

detta generalmente la forma di Kähler associata: è una metrica di Kähler se, e soltanto se, la forma Φ è chiusa, cioè se dΦ=0. Sullo spazio proiettivo ℙⁿ(ℂ) è definita una metrica di Kähler nota sotto il nome di metrica di Fubini-Study. Generalmente una sottovarietà complessa di una varietà kähleriana eredita la metrica ed è anch’essa una varietà kähleriana. In particolare, ogni varietà algebrica proiettiva è kähleriana.

→ Geometria differenziale; Matematica: problemi aperti