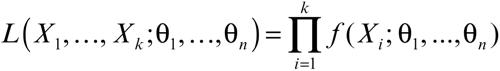verosimiglianza

verosimiglianza

verosimiglianza in probabilità e statistica, probabilità che un evento E sia condizionato a un evento H_i (Bayes → teorema di) appartenente a un insieme finito o numerabile di eventi incompatibili H; è quindi una funzione P: H → [0, 1], che a ogni evento H_i ∈ H associa la probabilità P(E |H_i). Più in generale, per funzione di verosimiglianza si intende una funzione di distribuzione di frequenza oppure una funzione di densità di probabilità ƒ(X; θ₁, ..., θ_n), considerata come funzione dei parametri θ₁, ..., θ_n relativi a una fissata variabile aleatoria X. Supponendo che {X₁, ..., X_k} sia un campione casuale estratto da una popolazione, di cui si conosce il tipo di distribuzione, ma di cui non si conoscono alcuni parametri, e considerata la ƒ(X; θ₁, ..., θ_n), allora la funzione di verosimiglianza L dei parametri del campione è così definita

dove X₁, ..., X_k sono considerati costanti. Le stime di massima verosimiglianza per i parametri sono i valori che massimizzano la funzione di verosimiglianza. Le funzioni che ne risultano

sono gli → stimatori di massima verosimiglianza per i parametri. Per esempio, si supponga che un’urna contenga 5 palline, θ delle quali bianche e le rimanenti rosse, e che in successive estrazioni con reimmissione siano state estratte una pallina bianca, una rossa e una bianca: campione che si può schematizzare con X = {B, R, B}. Il parametro θ da stimare sia la numerosità del carattere B nella popolazione (cioè nell’urna). Si possono allora assegnare i valori di probabilità P(«pallina estratta = B») = θ/5 e P(«pallina estratta = R») = 1 − θ/5. La funzione di verosimiglianza del campione è allora

che restituisce i valori

Il valore maggiore è 18/125, che si ottiene per θ = 3, per cui la stima di massima verosimiglianza per θ è 3. In generale, nel metodo di massima verosimiglianza, che consiste nello scegliere come stima del parametro il valore che massimizza la funzione di verosimiglianza, risulta più agevole massimizzare il logaritmo di tale funzione (perché trasforma il prodotto in somma) e quindi il valore di θ è una soluzione dell’equazione