vettore

vettore

vettore nozione suggerita originariamente dallo studio di grandezze fisiche, quali velocità, accelerazione, forza ecc. (dette grandezze vettoriali) la cui descrizione non può esaurirsi in un solo numero, come avviene per le grandezze scalari, quale è per esempio la temperatura. In senso più generale, il vettore è definito assiomaticamente come elemento costitutivo di uno → spazio vettoriale. Le grandezze vettoriali si possono correttamente descrivere soltanto precisando, oltre a una intensità o modulo, una direzione e un verso. Le notazioni più consuete per indicare un vettore sono una lettera soprassegnata con una freccia, come,

oppure una lettera in grassetto: u, v, ... Il modulo del vettore è indicato con |v| oppure v (tuttavia, quando si tratti di spazi di → Banach, e in particolare di spazi di → Hilbert, si usa per convenzione indicare i vettori con lettera corsiva non in neretto).

Due vettori di uguali modulo e direzione, ma di verso opposto, sono detti vettori opposti e se v è uno dei vettori, il suo opposto è indicato con −v. Un vettore di modulo 1 è detto vettore unitario oppure → versore; il vettore di modulo zero (che ha direzione e verso indefiniti) è detto vettore nullo ed è indicato con 0.

I vettori sono rappresentati comunemente con segmenti orientati: la direzione è indicata dalla retta cui appartiene il segmento, il verso da una freccia e il modulo dalla lunghezza del segmento (proporzionale all’intensità della grandezza rappresentata dal vettore). Due segmenti orientati aventi la stessa lunghezza, la stessa direzione e lo stesso verso sono detti equipollenti e la relazione di equipollenza è una relazione di equivalenza tra vettori applicati. Si definisce allora vettore libero, o semplicemente vettore, ogni classe di equivalenza di segmenti orientati equipollenti. I vettori della geometria elementare euclidea sono anche detti vettori geometrici. In ambito geometrico, un vettore determina una trasformazione detta → traslazione (si veda anche → spazio affine).

Se nelle applicazioni, in fisica o in geometria, interessa il punto A in cui è applicata una grandezza vettoriale, si parla di vettore applicato ed esso è indicato con una scrittura quale (A, B), B − A oppure

dove A è il punto di applicazione, o punto iniziale o origine del vettore applicato, mentre B ne è il punto o estremo finale.

Il vettore v_r, ottenuto proiettando un vettore v su una retta r, è detto il componente di v lungo la retta, mentre il modulo di v_r, preso con segno positivo o negativo a seconda che v_r abbia verso concorde o discorde rispetto a quello fissato su r, è detto la componente di v lungo la retta r. Introdotto nello spazio un riferimento cartesiano ortogonale Oxyz, a ogni vettore v si associano le componenti (ν_x, ν_y, ν_z) lungo gli assi, dette componenti cartesiane del vettore. Le componenti (ν_x, ν_y, ν_z) di un qualsiasi vettore v coincidono con le coordinate cartesiane del punto P, estremo finale del vettore applicato in O. Si stabilisce così una corrispondenza biunivoca tra vettori e terne ordinate di numeri reali e, nell’ordinario spazio tridimensionale dotato di riferimento, ogni vettore può essere perciò assegnato indicando le sue componenti: v = (ν_x, ν_y, ν_z). Note le componenti, il modulo o lunghezza del vettore è

Si osservi che, nell’ambito dell’algebra lineare, il modulo di un vettore è una particolare → norma (norma euclidea) e per questo si parla spesso di norma di un vettore v (indicata con ‖v‖), anziché di modulo.

Operazioni tra vettori

Tra i vettori si definiscono alcune operazioni che permettono di sviluppare un calcolo o algebra vettoriale, analoga a quella ordinaria tra numeri, che può essere espressa anche attraverso le componenti dei vettori.

• Addizione e sottrazione di vettori. Dati due vettori u e v, si applicano i due vettori in uno stesso punto P e si segue la regola del → parallelogramma (al vettore risultante si dà il nome, specialmente in fisica, di somma vettoriale). Il vettore somma w = u + v è il vettore che applicato in P coincide con la diagonale del parallelogramma uscente da P. L’operazione di addizione tra vettori è associativa e commutativa. Il vettore differenza u − v è determinato come somma dei vettori u e − v (opposto di v) ed è rappresentato dall’altra diagonale del parallelogramma, orientata da v verso u. La somma di due vettori opposti dà il vettore nullo 0. In termini di componenti, la somma di due vettori u = (u_x, u_y, u_z) e v = (ν_x, ν_y, ν_z) è il vettore u + v = (u_x + ν_x, u_y + ν_y, u_z + ν_z), ottenuto addizionando le componenti omologhe (si opera analogamente per la differenza).

• Moltiplicazione di uno scalare per un vettore (prodotto esterno). Dato un vettore v e un numero reale k, detto scalare, il prodotto dello scalare k per il vettore v è il vettore, indicato con kv avente il modulo uguale al numero reale |k| ⋅ |v|, la direzione coincidente con quella di v, verso identico a quello di v se k > 0, opposto a quello di v se k < 0. Se k = 0, il prodotto kv è dato dal vettore nullo. Se k = −1, il prodotto è −v, vettore opposto di v. Il vettore w = kv, le cui componenti si ottengono moltiplicando per k ognuna delle componenti di v, è anche detto multiplo del vettore v e i due vettori v e kv sono anche detti proporzionali. Si dice combinazione lineare dei vettori v₁, v₂, ..., v_k ogni vettore esprimibile nella forma h₁v₁ + h₂v₂ + ... + h_kv_k, con h₁, h₂, ..., h_k numeri reali. I vettori v₁, v₂, ..., v_k sono detti vettori linearmente dipendenti se esiste una loro combinazione lineare, a coefficienti non tutti nulli, uguale al vettore nullo; in caso contrario sono detti vettori linearmente indipendenti. Due vettori sono paralleli se e solo se sono linearmente dipendenti; tre vettori sono complanari se e solo se sono linearmente dipendenti. Indicati rispettivamente con i, j, k i versori paralleli agli assi x, y, z, del sistema di riferimento, ogni vettore v = (ν_x, ν_y, ν_z) può essere espresso come combinazione lineare di i, j, k, nella forma v = ν_xi + ν_yj +ν_zk.

• Altre operazioni. Tra i vettori sono anche definiti il → prodotto scalare (che dà come risultato un numero reale) e il → prodotto vettoriale (che dà come risultato un vettore) per i quali si rimanda alle voci relative. Si definiscono ortogonali (o perpendicolari) due vettori di uno spazio vettoriale euclideo il cui prodotto scalare è uguale a zero. Il vettore nullo 0 è perpendicolare a ogni vettore, compreso sé stesso. Un vettore ortogonale a sé stesso è detto → vettore isotropo.

Generalizzazioni

Se si prescinde da interpretazioni connesse con la fisica o l’ambiente geometrico euclideo tridimensionale, per vettore si può intendere qualunque n-pla ordinata di elementi di un campo K (che può essere R, l’insieme dei numeri reali, C, l’insieme dei numeri complessi, o un qualunque altro campo di scalari). In tale senso, un vettore è una particolare matrice e, in informatica, è implementato come un particolare tipo di dato (→ array).

Una matrice con una riga e n colonne

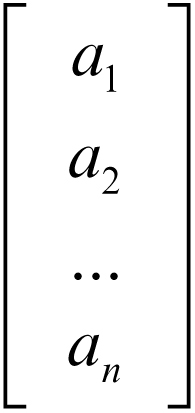
è così anche detta vettore riga, mentre una matrice con n righe e una colonna

è anche detta vettore colonna. In termini ancora più generali, un vettore è definito assiomaticamente come elemento di uno spazio vettoriale V su un campo K ed è esprimibile, a meno di isomorfismi, mediante una n-pla ordinata di elementi di tale campo (in tali contesti, come già osservato, un vettore è anche indicato con ν). I vettori geometrici in precedenza definiti ne sono un caso particolare: quello in cui la dimensione dello spazio è uguale a 3 e il campo degli scalari è R, insieme dei numeri reali. Tutti i vettori geometrici applicati in un punto O dello spazio euclideo costituiscono uno spazio vettoriale di dimensione 3 che si identifica, mediante un isomorfismo, con lo spazio vettoriale R³, i cui vettori sono le terne ordinate di numeri reali. Il campo K degli scalari può tuttavia essere un campo qualsiasi e la dimensione dello spazio può essere un qualunque numero naturale n oppure infinita. Il concetto di vettore, nato nell’ambito delle scienze fisiche, si presta quindi a generalizzazioni in svariate direzioni e, proprio per questo, trova numerose applicazioni in qualunque settore disciplinare in cui intervengano formalizzazioni matematiche (si veda anche → spazio metrico).