Vicino Oriente antico. Astronomia e astrologia
Vicino Oriente antico. Astronomia e astrologia
Astronomia e astrologia
Nella Mesopotamia antica l'osservazione e l'interpretazione del cielo volta a predire il futuro non era considerata meno 'scientifica' di quanto lo fosse il calcolo dei tempi di riapparizione in cielo di un pianeta: non esisteva quindi l'attuale distinzione tra astronomia e astrologia. Lo studio del cielo finalizzato a fare previsioni sul futuro, in quanto basato sulla serie dei presagi astronomici Enūma Anu Enlil, è stato trattato precedentemente (v. cap. IV, par. 2). L'elaborazione del calendario (v. cap. XII) fu anche un'importante motivazione che spinse a perfezionare la conoscenza dei fenomeni celesti. Nel presente capitolo sarà presa in considerazione l'evoluzione delle conoscenze sui movimenti dei pianeti, dai primi cataloghi stellari fino all'elaborazione dei complessi sistemi di calcolo tardobabilonesi. Nell'ultima parte si tratterà lo sviluppo dell'astrologia personale e degli oroscopi in epoca tardobabilonese, che pur iscrivendosi nella tradizione di divinazione sulla base dei presagi celesti tuttavia si fonda su dati astronomici relativi ai corpi celesti presenti nella fascia del percorso apparente del Sole nel cielo, lo Zodiaco.
Oltre al sistema di misura del tempo basato sulle unità di misura di lunghezza (v. cap. XII), a Babilonia esisteva un sistema usato soltanto in contesti astronomici, basato sulle unità di misura di peso manû (mina) e šiqlu (siclo di peso). L'unità manû corrispondeva a 1/6 di giorno, ossia a quattro ore, ed equivaleva a 60 šiqlu.
I primi cataloghi stellari
di Hermann Hunger
Sebbene identificare una stella con un nome non significhi propriamente fare astronomia, tuttavia tale attività era considerata così importante nella Mesopotamia antica che molti nomi di costellazioni tuttora in uso (ed ereditati dall'antica Grecia) hanno origini mesopotamiche: il Leone, lo Scorpione e il Toro ne sono chiari esempi. Non siamo in grado di dire se i confini delle costellazioni mesopotamiche fossero gli stessi di quelle dell'Almagesto di Tolomeo, del II sec. d.C.: non abbiamo, infatti, cataloghi stellari esaustivi in cuneiforme che possano essere paragonati direttamente all'opera tolemaica. Le più antiche liste di nomi di stelle, senza precisazioni sulla loro distribuzione nel cielo, risalgono alla prima metà del II millennio. Le stelle e le costellazioni sono soltanto una minima parte di queste liste che comprendono molti altri elementi del mondo naturale. Si cercava di compilarle in modo esaustivo perché potessero poi essere usate a scuola per insegnare la scrittura e il sapere di base.
I primi tentativi di conferire un ordine alle costellazioni sono i cosiddetti 'astrolabi'. Questo nome è totalmente fuorviante e fu dato a questi testi perché uno di essi era stato scritto su una tavoletta d'argilla circolare; il più antico esemplare risale al XII sec. a.C. Gli astrolabi contengono 12 sezioni, una per ogni mese di un anno generico, e ogni sezione registra tre costellazioni, ciascuna appartenente a uno dei tre cosiddetti 'sentieri' del cielo: il più settentrionale si chiama 'sentiero di Enlil', quello mediano 'sentiero di Anu', quello meridionale 'sentiero di Ea'. Questi sentieri sono sezioni dell'orizzonte orientale entro cui si possono vedere sorgere le costellazioni. I sentieri possono poi essere estesi fino a suddividere il cielo in sezioni. Secondo il compendio astronomico MUL.APIN, il Sole trascorre un quarto dell'anno in un sentiero e poi entra in quello adiacente. Se si considera questa descrizione geometricamente esatta, in termini moderni il sentiero di Enlil comprende tutte le stelle a nord di circa +17° di declinazione, il sentiero di Ea tutte le stelle a sud di circa −17° di declinazione, mentre il sentiero di Anu si trova tra questi due, su entrambi i lati dell'equatore celeste. È incerto se tali rigidi confini tra i sentieri siano mai stati presi in considerazione dagli astronomi babilonesi, che non conoscevano la trigonometria sferica. Comunque sia, essi ritenevano che le costellazioni avessero le loro 'levate eliache' (il sorgere contemporaneo al levarsi del Sole) all'interno dei rispettivi sentieri nel mese cui esse erano ascritte; sfortunatamente, questa ipotesi è però molto problematica. Tutto ciò non poteva essere rilevato senza una qualche schematizzazione, perché le costellazioni non sono distribuite nel cielo in modo da soddisfare le condizioni esposte nel testo; in conseguenza, per esempio, alcune costellazioni sono inserite in punti che non corrispondono alla loro reale posizione. Inoltre, sono elencati anche i pianeti; tuttavia, le loro rispettive levate eliache in un calendario lunare non possono mai verificarsi ogni anno nella stessa data.
Gran parte delle nostre conoscenze circa le cognizioni astrali babilonesi nei primi secoli del I millennio a.C. viene dalla raccolta MUL.APIN, ossia 'Stella Aratro', chiamata così dall'incipit del testo. Sebbene non tutte le sue parti siano state compilate simultaneamente, è plausibile che il testo sia stato composto intorno al 1000 a.C.; gli esemplari conservati risalgono al 687 a.C. e oltre. Il testo contiene innanzitutto un catalogo delle stelle, distribuite sulla base dei tre suddetti sentieri. Originariamente, vi erano probabilmente elencate 60 costellazioni, tutte invisibili per un certo periodo, oltre a sei costellazioni circumpolari e ai cinque pianeti allora conosciuti; 33 costellazioni, più le 6 circumpolari e Giove, nel sentiero di Enlil; 23 costellazioni e i quattro pianeti restanti nel sentiero di Anu; 15 costellazioni nel sentiero di Ea. Le date delle levate eliache di 35 costellazioni (indicate anche in questo primo catalogo) sono raccolte in una seconda lista, all'interno di un calendario ideale di 12 mesi di 30 giorni ciascuno. Poiché tutte le date sono divisibili per 5, è ovvio che possono soltanto essere approssimative, e pertanto questo elenco deve essere usato con molta cautela se si vogliono identificare le stelle. La lista contiene anche le date dei solstizi e degli equinozi, che sono fissati nel quindicesimo giorno del I, IV, VII e X mese. Anche queste date potrebbero essere soltanto approssimative: s'indicava che tali date dovevano essere collocate all'interno di quei mesi specifici, ma la loro individuazione si otteneva per mezzo di un'adeguata intercalazione (v. oltre).
Nel compendio sono fornite anche una lista delle costellazioni che sorgono quando altre tramontano (le levate e i tramonti simultanei sono indipendenti dalle date del calendario e possono quindi risultare più attendibili al fine di identificarle) e due liste di stelle che culminano vicino allo zenit, le quali sono chiamate ziqpu: "Le stelle ziqpu, che si trovano nel sentiero di Enlil al centro del cielo, di fronte all'osservatore, permettono di vedere il sorgere e il tramontare delle altre stelle nella notte". Queste stelle erano usate per indicare con esattezza l'ora durante la notte o, per esempio, in occasione di un'eclissi: alcuni esempi di questo tipo di calcolo del tempo compaiono in alcune lettere indirizzate a re assiri risalenti all'VIII-VII secolo. Inoltre, sono elencate le costellazioni costeggiate dalla Luna nel suo ciclo mensile. Sono nominate 17 costellazioni (non vi è ancora traccia di uno Zodiaco diviso in 12 sezioni) e si sostiene che i cinque pianeti e il Sole si muovono tutti lungo il sentiero della Luna.
A questi elenchi seguono una descrizione dei fenomeni planetari con i loro rispettivi periodi di visibilità e di invisibilità, indicati però in modo molto approssimativo, e l'esposizione delle regole per l'intercalazione. Poiché 12 mesi lunari non equivalgono esattamente a un anno solare, i Babilonesi aggiungevano un mese quando necessario (v. cap. XII). Le regole nel testo forniscono date teoriche per il levare eliaco di alcune stelle; se queste fossero state in ritardo rispetto alle date indicate, si rendeva necessaria l'intercalazione. Per esempio: "Se Sirio diventa visibile il quindicesimo giorno del IV mese, l'anno in questione è normale; ma se Sirio è visibile il quindicesimo giorno del V mese, l'anno sarà intercalare". In un'osservazione finale si assume semplicemente che sia necessario eseguire l'intercalazione ogni tre anni.
Infine, la raccolta MUL.APIN, contiene due tavole, la tavola delle ombre per l'omonimo orologio solare e la tavola dei deflussi per l'orologio ad acqua. Nella tavole delle ombre è indicato, per i giorni dei solstizi e degli equinozi, a quale ora del giorno la lunghezza dell'ombra di un'asticella verticale (probabilmente lunga 1 cubito) raggiunge uno, due o più cubiti: negli equinozi si considerano lunghezze fino a 3 cubiti e nei solstizi fino a 10 cubiti (i 7 cubiti intermedi sono omessi per motivi di calcolo). Le ore erano calcolate dividendo alcuni numeri fissi (3 per il solstizio estivo, 2,5 per gli equinozi e 2 per il solstizio invernale) per il numero dei cubiti della lunghezza dell'ombra. Otto Neugebauer ha mostrato come il calcolo delle ore del giorno debba in realtà essere interscambiato nel caso dei due solstizi; se così fosse, si avrebbe però un'ombra costante a mezzodì e ciò non corrisponde ai fenomeni osservabili. Una notevole conseguenza dell'osservazione di Neugebauer è che in questo testo si ritroverebbe implicitamente il rapporto 3:2 tra la maggiore e la minore durata della luminosità diurna, che è attestato soltanto in testi matematico-astronomici successivi. Infatti, per gran parte della storia mesopotamica, si assunse che il rapporto tra il dì (qui inteso come arco diurno, ossia come periodo di tempo dall'alba al tramonto del Sole) più lungo e quello più corto fosse di 2:1, che non corrisponde però a quello effettivo, considerando la latitudine della zona. Il rapporto 2:1 è indicato per la prima volta in una tavoletta della prima metà del II millennio e rimase in vigore per almeno 1000 anni, come dimostrano chiaramente altri testi. Si è dunque costretti ad ammettere che la divergenza di questo rapporto dalla realtà naturale non turbò gli astronomi per molto tempo, e soltanto in testi astronomici del IV sec. è esplicitamente usato il rapporto più corretto di 3:2. Valori più accurati non furono mai adottati, essendo la forma sferica della Terra una nozione sconosciuta nell'antica Mesopotamia.
Nella tavola dell'orologio ad acqua a deflusso era indicato, all'inizio e a metà di ogni mese in un calendario ideale, un certo valore di peso, che serviva da 'orologio della notte'. Si assumeva, infatti, che questo peso corrispondesse a quello dell'acqua che al tramonto del Sole doveva essere versata nell'orologio ad acqua in modo che, alla fine della notte di una certa data, esso risultasse vuoto. I pesi variavano con la stagione, così che un minimo di 2 mine (1 kg ca.) era fissato per la metà del 4° mese e un massimo di 4 mine per la metà del 10° mese; tra queste due date, il peso aumentava o diminuiva con una differenza costante di 10 sicli (ossia un sesto di mina, circa 84 g) ogni metà mese. Essendo i pesi proporzionali al tempo notturno, ne risulta il rapporto, errato per la Mesopotamia, di 2:1 tra la notte più lunga e quella più corta. Neugebauer ha tentato di trovarne una spiegazione costruendo alcuni orologi ad acqua ed esaminando le proprietà del deflusso idrico, ma è ormai certo che quel rapporto s'intendeva riferito al tempo, e non al peso dell'acqua. Il rapporto più appropriato di 3:2 introdotto nella tavola delle ombre, seppur anch'esso non corretto per Babilonia, è comunque un'approssimazione accettabile per il calcolo astronomico della seconda metà del I millennio a.C.
La tavola dell'orologio ad acqua fornisce anche il tempo che intercorre tra il tramonto del Sole e quello della Luna all'inizio di ogni mese e il tempo che intercorre tra il tramonto del Sole e la prima apparizione della Luna a metà di ogni mese, in occasione della Luna piena; questi intervalli equivalgono a 1/15 della durata di un'intera notte. Nel seguito, il compendio MUL.APIN si occupa di presagi celesti che non presentano alcun nesso con le sezioni astronomiche che li precedono; non è chiaro, dunque, il motivo del loro inserimento nel testo.
La lista delle costellazioni presentata nelle prime sezioni del compendio Stella Aratro non è un catalogo stellare completo, se non altro perché in altri testi babilonesi compaiono molti nomi di stelle assenti in esso. Anche altri testi, che elencano stelle o costellazioni in base a certe relazioni tra loro, non sono esaurienti. Tra queste diverse liste di stelle, ve n'è una che le ordina in base a una serie di 'corde', ciascuna includente tre o quattro stelle: esse sembrano scelte in modo tale da poter essere osservate allineate lungo una linea retta, come quella rappresentata da una corda tesa, forse usata in uno strumento d'osservazione. Questa assunzione è valida per molte delle stelle elencate (sempre che si possa identificarle con certezza); altre stelle, invece, non sembrano rientrare all'interno di questo criterio di catalogazione o forse non sono identificate correttamente. Un altro di questi testi raggruppa le stelle secondo forme geometriche (non facilmente comprensibili) e in base alla distanza uguale (o doppia) che le separa. Poiché molte delle stelle elencate non compaiono in altre fonti, è impossibile decidere secondo quali criteri siano state ordinate; se, d'altronde, tali criteri fossero chiari, il testo potrebbe essere d'aiuto per l'identificazione delle stelle. Inoltre, ci è pervenuto un catalogo delle stelle vicine all'eclittica, con annesse le loro 'longitudini'; queste stelle erano usate come punti di riferimento nella composizione dei diari astronomici (v. oltre).
Infine, quattro tavole riguardanti la Luna sono inserite nella grande serie di presagi Enūma Anu Enlil (v. cap. IV, par. 2). Si tratta della tavoletta XIV della raccolta: le prime due tavole indicano la durata della visibilità della Luna per ogni giorno del mese vicino a un equinozio, espressa secondo le due diverse modalità di misura del tempo (basate rispettivamente sulle unità di misura di lunghezza e sulle unità di misura di peso). La terza tavola fornisce la variazione stagionale della durata del dì e della notte a intervalli di quindici giorni. Il rapporto tra il dì (o la notte) più lungo e il dì (o la notte) più corto è di 2:1. La quarta tavola, anch'essa ordinata secondo intervalli di quindici giorni, indica per l'inizio di ogni mese (quindi dopo la Luna nuova) il tempo che intercorre tra il tramonto del Sole e quello della Luna, e a metà di ogni mese (cioè in prossimità della Luna piena), invece, il tempo che intercorre tra il tramonto del Sole e l'apparizione della Luna. Si assume che entrambi gli intervalli siano 1/15 della durata della notte; anche questa durata varia, come nella tavola precedente, di modo che il rapporto tra la notte più lunga e quella più corta sia ancora una volta di 2:1. Questa tavola è simile alla tavola dell'orologio ad acqua del compendio Stella Aratro.
Le osservazioni astronomiche
di Hermann Hunger
A partire dalla metà dell'VIII sec., al più tardi, iniziarono a essere eseguite osservazioni astronomiche sistematiche. Sono conservate (benché in copia) cronache di eclissi risalenti a quell'epoca e il primo diario astronomico databile risale al 652. La corrispondenza tra i re assiri e i loro consiglieri (VII sec.), nella quale sono trattate spesso questioni astronomiche connesse ai presagi celesti (anche se probabilmente il re non era interessato ai dettagli astronomici), ci consente di valutare le conoscenze degli esperti. Essi conoscevano i diversi fenomeni planetari e la loro sequenza e avevano anche un'idea approssimativa degli intervalli di tempo che intercorrevano tra di essi e quindi, a volte, erano in grado di asserire con certezza che un pianeta nel suo moto retrogrado non sarebbe entrato in una certa costellazione; sapevano anche stabilire quando le eclissi erano improbabili e quando, invece, era opportuno tenere la situazione sotto controllo ed erano in grado di annunciare le eclissi lunari con alcuni giorni d'anticipo; non erano invece in grado di calcolare i fenomeni lunari o planetari per mezzo di tavole (come avvenne in seguito), ma potrebbero aver cominciato ad annotare osservazioni simili a quelle dei diari astronomici, sebbene a Ninive non sia stata trovata alcuna prova a tale riguardo.
Nei testi cuneiformi concernenti le osservazioni astronomiche alcune date del calendario sono il risultato di calcoli e non di osservazioni; in questi casi non ha senso cercare quale osservazione abbia determinato una certa data e tanto meno valutarne la precisione. Questi schemi di calcolo sono adoperati per stabilire alcuni fenomeni osservabili come solstizi ed equinozi, il sorgere e il tramonto eliaco dei pianeti (ossia, come detto in precedenza, contemporaneo al levare del Sole), oltre che il levare acronittico (ossia contemporaneo al tramonto del Sole) della stella Sirio. È possibile che, originariamente, vi fosse uno schema di calcolo riguardante il solstizio d'estate e che gli altri punti cardinali dell'anno fossero semplicemente distribuiti il più possibile a intervalli regolari; in questa maniera, gli intervalli erano di 3 mesi e 3 giorni, eccetto i 3 mesi e 2 giorni che separavano l'equinozio primaverile dal solstizio d'estate. Alla stessa maniera, i fenomeni riguardanti Sirio si verificavano a intervalli regolari a partire dal solstizio d'estate.
Le date calcolate secondo schemi prestabiliti sono collegate al ciclo di 19 anni (di cui sette anni intercalari) che regolava il calendario in uso a partire dal 500 (v. cap. XII). Per esempio, in una tavoletta molto frammentaria che contiene una tavola di date calcolate, ogni data ha una differenza con quella relativa all'anno successivo di 11;3.10 giorni (cioè 11,26 giorni) oppure di 11;3.10 unità e un multiplo di 30: il numero 30 indica, naturalmente, la durata di un mese e poiché la durata media di un mese babilonese è minore di 30 giorni, l'unità di misura in questo caso non era il giorno, bensì la trentesima parte di un mese sinodico medio. Il vantaggio di usare questa unità di misura (adoperata nell'astronomia indiana con il nome di tithi, v. oltre) è facilmente riscontrabile dal fatto che per trovare le date dei vari fenomeni celesti non occorre più conoscere le durate dei singoli mesi, in quanto la data espressa in tithi può essere usata semplicemente omettendo tutte le parti frazionarie; in questa maniera, l'errore è al massimo di un giorno. Di conseguenza, era possibile adoperare una versione semplificata dello schema di calcolo, nella quale le parti frazionarie erano omesse e, da un anno a quello successivo, si aggiungevano 11 giorni alla data; a un certo punto, nell'arco di 19 anni, a causa della parte frazionaria trascurata, era necessario però fare intervenire una differenza di 12 giorni.
I testi di osservazioni astronomiche possono essere suddivisi in quattro gruppi: diari astronomici, pronostici per l'anno successivo, almanacchi di 'stelle normali', ossia di stelle di riferimento vicine all'eclittica, ed estratti di osservazioni planetarie e lunari.
I diari astronomici
I testi cuneiformi contenenti osservazioni effettuate in ordine cronologico, noti come 'diari astronomici', erano chiamati dai Babilonesi 'osservazioni regolari'. La procedura per comporli era la seguente. Gli appunti relativi alle osservazioni effettuate erano registrati su tavolette di argilla fino a quando tali tavolette potevano essere mantenute umide per incidere i segni. Tutti questi appunti erano raccolti e, in seguito, ne erano fatte delle copie che comprendevano osservazioni svolte nell'arco di sei mesi; i diari semestrali erano, a loro volta, conservati in archivi. La maggior parte del materiale ritrovato (circa 1200 frammenti) proviene dalla città di Babilonia ed è conservata nei musei europei, soprattutto nel British Museum di Londra. Purtroppo, queste tavolette non furono scoperte durante scavi autorizzati; non si conosce quindi la loro precisa provenienza e se esse fossero conservate in templi oppure in abitazioni private. Esse coprono un arco di tempo che va dal VII al I sec., anche se la maggior parte risale al IV e II secolo; poiché quasi tutte sono frammentarie, le loro osservazioni riguardano soltanto il 5% ca. di tutto questo arco di tempo.
I diari presentano le osservazioni in sezioni mensili. In ogni sezione è indicata innanzitutto la durata del mese precedente (se esso ha avuto 29 o 30 giorni); segue poi il tempo che intercorre tra il tramonto del Sole e quello della Luna la prima sera del mese e altre circostanze legate alla prima visibilità della Luna. Nel corso del mese, la posizione della Luna è indicata con riferimento ad alcune stelle vicine all'eclittica, chiamate 'stelle normali' dagli studiosi moderni: la Luna è localizzata o 'prima' o 'dopo', o 'sopra' o 'sotto' queste stelle, ma non è chiaro se secondo direzioni parallele all'eclittica, all'orizzonte o ad altro ente. La distanza è data in unità di lunghezza, che erano adoperate anche per misurare le distanze (angolari) nel cielo, e precisamente: il cubito (sumerico KÙŠ, accadico ammatu) e il suo sottomultiplo, il dito (sumerico ŠU.SI, accadico ubānu); dall'equivalenza 1 cubito=24 dita=2 UŠ ('gradi': i gradi sessagesimali, di simbolo '°', tuttora in uso, che furono introdotti appunto dai Babilonesi), si desume che 1 dito equivaleva a 0;5° (cioè 1/12°) e 1° equivaleva a 12 dita. Comunque, le misurazioni non sembrano essere molto accurate: a una distanza di oltre 1 cubito si assegna un errore di 4 larghezze di dito e a distanze di oltre 3 cubiti un errore di 1/3 di cubito. Non è noto come queste misure fossero trasformate in longitudine e latitudine celeste (ammesso che ciò sia stato fatto). Ci è pervenuto un frammento di un catalogo relativo a queste stelle normali con le loro rispettive 'longitudini'; per queste ultime risulta un errore per difetto di circa 4,5° rispetto ai calcoli moderni.
Erano osservati sei intervalli di tempo relativi alla Luna. Oltre al tempo intercorrente tra il tramonto del Sole e quello della Luna all'inizio del mese, erano registrati, nel periodo di Luna piena, gli intervalli dal tramonto della Luna al sorgere del Sole, e viceversa al mattino, e dal sorgere della Luna al tramonto del Sole, e viceversa alla sera; verso la fine del mese, nell'ultimo giorno di visibilità lunare, era calcolato, infine, l'intervallo tra il sorgere della Luna e quello del Sole. Questi intervalli erano usati probabilmente per studiare la periodicità del moto lunare. Nei diari, inoltre, erano descritte in dettaglio le eclissi di Sole e di Luna. Anche quando un'eclissi lunare non era visibile a Babilonia, era comunque menzionata nei diari. Per le eclissi di Sole era indicata soltanto la loro possibilità; i Babilonesi conoscevano, infatti, la periodicità di queste eclissi, ma non sapevano prevedere in quale punto della Terra sarebbe stato possibile osservarle poiché non conoscevano la forma della Terra né la distanza dalla Terra al Sole e alla Luna. I diari annotavano le date in cui i pianeti spariscono e riappaiono, nonché i loro punti stazionari. Come nel caso della Luna, era registrato anche il passaggio di un pianeta in prossimità di una stella normale. Eventi eccezionali come le comete o le meteore si trovano citati occasionalmente nei diari; la cometa di Halley, per esempio, fu avvistata sia nel 164 che nell'87 a.C.
Al termine di ogni sezione mensile dei diari sono elencati i prezzi di sei merci importanti, incluse le loro variazioni nel corso del mese; segue quindi la misura del livello del fiume Eufrate e delle sue variazioni; infine, sono menzionati gli eventi più importanti avvenuti nella città di Babilonia o nella regione. Queste informazioni hanno generalmente soltanto un interesse locale, ma a volte anche la storia lascia le sue tracce: per esempio, vi è registrata, senza alcun commento, la morte di Alessandro Magno. Infine, i diari si occupano anche del tempo atmosferico, oltre che delle osservazioni astronomiche, sia perché i fenomeni atmosferici hanno luogo anch'essi in cielo, sia perché lo stato del cielo condiziona le osservazioni astronomiche. La terminologia relativa è comprensibile soltanto in parte, ma sono citati diversi tipi di nuvole e di piogge. Sono stati conservati anche alcuni testi che descrivono le condizioni atmosferiche di interi periodi, ma sembra che non siano basati su diari.
I diari astronomici rappresentano una delle più imponenti e certamente la più longeva impresa scientifica della storia dell'umanità. Per almeno settecento anni furono raccolti, compilati, conservati e, se necessario, ricopiati dati astronomici, e tutto ciò indipendentemente dal fatto che si fosse in tempo di pace o di guerra, e a dispetto di possibili rivolte politiche, invasioni straniere o disastri economici. Esistono documenti legali che illustrano come nel II sec. gli astronomi lavorassero per conto del tempio di Marduk a Babilonia. Non sappiamo chi sostenesse la loro attività in precedenza, ma è possibile che durante gli imperi assiro e babilonese fosse stata la stessa amministrazione regia. Si è ipotizzato che queste osservazioni fossero fatte allo scopo di condurre indagini matematico-astronomiche sui movimenti della Luna e dei pianeti, poiché siamo in possesso dei risultati di questo studio, vale a dire dei calcoli relativi ai fenomeni caratteristici (v. oltre). Tale spiegazione, tuttavia, non è valida per tutto il materiale contenuto nei diari. Forse ci si aspettava di individuare una periodicità nel tempo meteorologico, nel livello dei fiumi e nei prezzi, che poteva essere individuata solamente attraverso uno studio prolungato (ciò non si applica però agli eventi storici). Certamente il contenuto astronomico dei diari fu di grande utilità, come dimostrano i testi astronomici non matematici conservati, i quali derivano chiaramente da diari, e i testi di carattere matematico, ove tale derivazione è probabile.
Pronostici, almanacchi e altri testi
Un altro gruppo di testi che contengono osservazioni astronomiche, anche se sono organizzati diversamente dai diari, è quello dei pronostici relativi a un anno prescelto, documentati dal III al I sec. a.C. Era noto che uno specifico fenomeno planetario, come, per esempio, la prima visibilità a est di un pianeta dopo l'invisibilità dovuta alla congiunzione con il Sole, si verificava lo stesso (o quasi lo stesso) giorno dell'anno solare dopo un certo numero di anni: si trattava cioè di fenomeni periodici. Di conseguenza, avendo a disposizione osservazioni planetarie di uno o due secoli (come quelle contenute proprio nei diari astronomici), questi intervalli o periodi potevano essere facilmente dedotti a partire da quei dati. I periodi usati erano i seguenti: 46 anni per Mercurio, 8 per Venere, 47 o 79 per Marte, 71 o 83 per Giove, 59 per Saturno. Quindi, una volta capito dopo quanti anni un fenomeno si ripresentava nella stessa data, i diari potevano essere usati per fare previsioni: bastava selezionare accuratamente osservazioni anteriori di un numero di anni uguale al periodo rispetto alla data scelta. Con questa tecnica era possibile compilare testi che contenessero, per un certo anno prescelto, le osservazioni di fenomeni planetari periodici estrapolate da diari antecedenti di un periodo l'anno in questione.
Considerato il fatto che alle previsioni astronomiche babilonesi non era richiesta un'estrema precisione, il metodo di assumere determinati anni come mete prescelte per il computo di fenomeni planetari periodici, aveva un discreto successo nella previsione di eventi futuri. Tuttavia, erano necessarie alcune correzioni per ottenere risultati più attendibili; è incerto, però, se e come queste correzioni siano state operate. Tale metodo richiedeva naturalmente la consultazione di diversi diari; inoltre, questi ultimi dovevano essere letti integralmente, perché i fenomeni planetari potevano essere annoverati in un punto qualsiasi di un diario. Una condizione indispensabile per poter compilare un testo concernente tutti i fenomeni planetari di un determinato anno era dunque avere a disposizione un archivio completo dei diari. Infatti, questi testi sono fonti storiche relative alle osservazioni astronomiche valide tanto quanto i diari, e quindi costituiscono un utile supplemento al corpus piuttosto frammentario dei diari.
Il termine 'almanacco' è usato modernamente per fare riferimento a un altro gruppo di testi che i Babilonesi chiamavano "misurazioni relative all'entrata dei pianeti [nei diversi segni dello Zodiaco]". Ciascun almanacco si occupava di un intero anno, suddiviso in 12 o 13 sezioni, una per ciascun mese. All'inizio di ogni sezione mensile era indicata la durata del mese precedente; seguiva quindi un sommario dove era indicata la posizione dei pianeti rispetto allo Zodiaco all'inizio del mese; verso la metà del mese era indicata la data in cui la Luna tramontava per la prima volta dopo il sorgere del Sole; infine, in coincidenza della fine del mese era indicata la data dell'ultima visibilità della Luna. Le eclissi solari e lunari erano elencate con data e ora del giorno. Le eclissi che avevano luogo in una fase del giorno in cui non potevano essere osservate erano segnalate con la dicitura "ignorate". Le eclissi solari, se erano teoricamente visibili, erano menzionate invece con l'espressione "da osservare"; i Babilonesi non erano, infatti, mai certi che esse fossero effettivamente visibili a Babilonia. La prima e l'ultima visibilità dei pianeti, nonché i loro punti stazionari, erano elencati per data e segno zodiacale. Inoltre, era indicata la data dello spostamento di un pianeta da un segno zodiacale a un altro: da qui il nome, ricordato dianzi, con cui i Babilonesi indicavano questi testi. Gli almanacchi fornivano anche le date dei solstizi, degli equinozi e dei fenomeni di Sirio, secondo uno schema collegato al ciclo che regola l'intercalazione. I cosiddetti almanacchi di stelle normali, molto simili agli almanacchi appena descritti, contengono inoltre dati relativi al passaggio della Luna e dei pianeti in prossimità delle stelle normali.
Infine, sono state trovate un certo numero di tavolette, anch'esse compilate sulla base di dati tratti dai diari, che contengono osservazioni relative a uno oppure due pianeti.
L'astronomia matematica nel periodo tardobabilonese
di Hermann Hunger
Nella seconda metà del I millennio a.C. i Babilonesi elaborarono un'astronomia a carattere matematico, attestata da alcune centinaia di frammenti di tavolette di argilla, la maggior parte delle quali furono trovate da scavatori clandestini nelle città di Uruk e Babilonia. Possono esserci state altre città nella bassa Mesopotamia dove si eseguivano questi calcoli astronomici, ma finora non esistono prove a questo riguardo. Dopo le prime scoperte di J. Epping, fu soprattutto grazie a F.X. Kugler e ad O. Neugebauer che si arrivò a una graduale comprensione di questi documenti e alla loro pubblicazione. Tuttavia, non è ancora possibile tracciare un resoconto storico dell'astronomia matematica babilonese: anche se molte tavolette possono essere datate, le loro relazioni reciproche non sono sempre chiare. Esistono due gruppi principali: i testi contenenti tavole numeriche, chiamate anche 'effemeridi' perché presentano date e posizioni dei pianeti in ordine cronologico, e i testi che descrivono le procedure di calcolo per ottenere le effemeridi. A questi due gruppi principali bisogna aggiungere le tavole ausiliarie. Le tavolette provengono dalle città di Babilonia (non si conosce esattamente il loro luogo di provenienza all'interno della città) e Uruk (in questo caso esse sono state trovate in un complesso templare); infine, i testi possono essere classificati, secondo gli strumenti matematici (aritmetici) utilizzati, come appartenenti al 'sistema A' o al 'sistema B' (v. oltre). Non tutte le tavolette rientrano perfettamente in queste categorie, e non ci sono correlazioni precise tra di esse. Entrambi i sistemi A e B sono attestati sia a Uruk che a Babilonia: disponiamo, per un ampio arco di tempo, di tavolette provenienti da tutte e due le città e compilate in tutti e due i sistemi. Sebbene le tavolette più antiche (risalenti al IV sec.) possano essere ascritte al sistema A, ciò non implica che il sistema A sia il più antico, e non è dato neppure riscontrare un'intrinseca superiorità di un sistema sull'altro; si può affermare, usando la terminologia moderna, che il sistema B riesce ad approssimare in modo migliore le funzioni sinusoidali, ossia le funzioni periodiche che servono a descrivere i fenomeni planetari, mentre il sistema A è più indicato per fare predizioni.
In queste tavolette non compaiono mai dimostrazioni o giustificazioni delle procedure di calcolo o di compilazione seguite, né si hanno indicazioni di concetti geometrici collegati ai calcoli; per esempio, non è stata conservata alcuna rappresentazione grafica dei movimenti stellari. Nelle tavole la posizione dei pianeti è data usando l'unità di misura che modernamente è chiamata 'grado sessagesimale' (si tratta dei gradi angolari da noi tuttora usati, che hanno origine babilonese) e che corrisponde alla 360esima parte dell'eclittica in termini astronomici e alla 360esima parte dell'angolo giro in termini angolari. Tuttavia, dai testi astronomici non ci è dato sapere se i Babilonesi supponessero un moto circolare dei pianeti o secondo qualche altra figura geometrica: tali assunzioni non erano, infatti, necessarie per calcolare le effemeridi. Né siamo in grado di stabilire se considerassero il cielo sferico; sebbene ciò sia possibile, per la loro astronomia, non era di alcuna importanza. Di fondamentale importanza è invece lo strumento matematico impiegato: il sistema di numerazione posizionale sessagesimale, adoperato dapprima in testi di problemi aritmetici e geometrici, anche legati ad applicazioni pratiche (v. cap. XI), e che soltanto più tardi fu usato per esprimere rapporti riguardanti i fenomeni celesti.
Le moderne effemeridi astronomiche forniscono le posizioni dei corpi celesti a intervalli di tempo regolari. Non era questo però lo scopo principale dei Babilonesi, i quali erano interessati soprattutto a specifici fenomeni di un pianeta, come la sua prima e la sua ultima visibilità o i suoi punti stazionari. Le tavole babilonesi, quindi, elencano in righe successive le successive occorrenze di un dato fenomeno, indicando per ognuna di esse la data e la posizione del pianeta. A causa dell'irregolarità dei moti planetari, le distanze tra due fenomeni successivi, per quanto riguarda sia il tempo che la posizione, sono diseguali, e possono variare da un massimo a un minimo. Questa oscillazione di valori si verifica spesso: il primo esempio documentato a Babilonia concerne la durata del dì e della notte (v. sopra). Tale variazione era trattata mediante una successione di numeri con una differenza costante: partendo da un valore iniziale, si calcolavano i valori successivi semplicemente aggiungendo una quantità (differenza) costante. Qualora tale procedura avesse condotto a un risultato che eccedeva il limite massimo previsto, la quantità in eccesso era sottratta dal massimo, dando così un risultato inferiore a quest'ultimo. Da qui in poi, la differenza doveva essere sottratta per ogni passaggio successivo fino a raggiungere il valore minimo. Se invece si raggiungeva un valore al di sotto del minimo, l'eccesso era aggiunto a sua volta al minimo, e di nuovo s'invertiva la procedura: anziché sottrarre la differenza, la si aggiungeva.
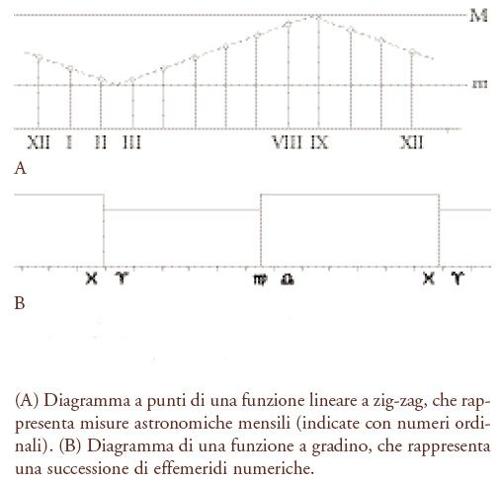
Se si rappresentano graficamente i valori ottenuti con questo procedimento, si ottiene una linea che gli autori moderni chiamano 'funzione lineare a zig-zag' (fig. 6A): di un disegno di tale linea non è mai stata trovata traccia nelle tavolette d'argilla, né è documentato alcun nome babilonese per una tale figura. È possibile usare formule moderne per descrivere questa funzione a zig-zag, tenendo presente che la notazione algebrica moderna non ha una controparte nella cultura scientifica babilonese ed è solamente un espediente per aiutarci a descrivere delle relazioni aritmetiche. Per la successione numerica descritta, con differenza d, massimo M, e minimo m, è possibile calcolare il 'periodo', P=2(M−m)/d, il quale però non è necessariamente un numero intero (nella maggior parte dei casi non lo è): ciò significa che un periodo non contiene un numero intero di occorrenze di uno stesso fenomeno. Vi è tuttavia un periodo più lungo, Π, che è definito dal ritorno della funzione allo stesso valore numerico; si ha Z=Π/P, ove Z è il numero di variazioni cicliche dopo le quali la funzione ritorna allo stesso valore numerico. Nella maggior parte dei casi, Π è un numero grande, e questo aiuta a datare le tavolette: poiché i valori numerici di una data funzione si ripetono soltanto dopo secoli, conoscendo il contesto storico si perviene a un'unica datazione.
Un'altra maniera di rappresentare successioni numeriche come quelle presenti nelle tavolette babilonesi di effemeridi è attraverso le cosiddette 'funzioni a gradino' (fig. 6B): in una tale funzione il valore della funzione rimane costante per un certo intervallo, poi salta a un valore diverso per un altro periodo di tempo, e così via (i testi babilonesi ‒ è bene ribadirlo ‒ contengono soltanto numeri, non diagrammi). Il numero di questi salti può variare, ma per ragioni pratiche esso è sempre modesto; nei testi ne sono indicati da 2 a 6. A partire dai valori dati da una determinata funzione a gradino y si può definire una seconda funzione z che rappresenta la successione numerica ottenuta per addizione e sottrazione di una differenza, nel modo seguente: z(n+1)=z(n)+y(n+1), dove z(n) sta a indicare il valore della funzione z nel passo n-esimo. Neugebauer chiamava y 'funzione-differenza' di z, e z 'funzione-somma' di y. La differenza da aggiungere per calcolare i valori di z rimane costante finché y ha lo stesso valore; quando si arriva a un punto di salto tra due diversi valori numerici di y, la differenza sarà ottenuta da quantità proporzionate derivanti da entrambi i valori numerici.
La differenza fondamentale tra i due metodi di calcolo, la funzione a zig-zag e la funzione a gradino, può essere utilizzata per classificare le tavole babilonesi: in conseguenza, quelle basate su funzioni a gradino sono generalmente ascritte al sistema A, quelle basate su funzioni a zig-zag al sistema B.
Le tavole planetarie combinano due o tre successioni numeriche del genere appena descritto per calcolare date e posizioni dei fenomeni planetari, sulla base di periodi simili a quelli usati nei predetti pronostici riguardanti un anno prescelto, anche se i testi matematico-astronomici utilizzano periodi più lunghi e più accurati. Grazie a questa accuratezza, l'errore cumulativo è minimo, anche quando le tavole sono calcolate per interi secoli con gli stessi parametri. Nella Tav. I sono date notizie sulle procedure di calcolo. Trascorse molto tempo prima di ottenere risultati soddisfacenti; nel materiale a nostra disposizione si ritrovano diversi insiemi di parametri per ogni pianeta, che potrebbero corrispondere a diversi tentativi a opera di diverse persone. Non ci è pervenuto nulla circa possibili discussioni tra astronomi babilonesi, anche se è molto improbabile che si sia considerato opportuno metterle per iscritto. È chiaro, comunque, che furono trovati dei compromessi tra le osservazioni planetarie e le convenienze utili a semplificare le procedure di calcolo: quei numeri 'così precisi' usati per comporre le tavole non possono essere stati il risultato di osservazioni.
Le tavolette riguardanti le effemeridi lunari sono più ampie di quelle relative ai pianeti perché i Babilonesi pensavano che il tempo e la longitudine della Luna in occasione della sua prima visibilità o in fase di opposizione con il Sole risultassero da più componenti (Tav. II e Tav. III).
Sembra infatti che essi siano stati i primi a ipotizzare che un fenomeno complesso potesse risultare dalla somma di altri più semplici, e furono anche i primi a studiare ciascun fenomeno separatamente. Come nel caso dei pianeti, le tavole lunari possono essere classificate secondo la loro appartenenza al sistema A (funzione a gradino) oppure al sistema B (funzione a zig-zag). La differenza risiede nel modo in cui è trattato il moto delle sizigie ‒ ossia le posizioni di congiunzione con il Sole (Luna nuova) o di opposizione della Luna (Luna piena), che in ogni lunazione viene a trovarsi due volte sulla stessa linea del Sole e della Terra. Più precisamente detta differenza risiede nel modo in cui è rappresentata la velocità solare, mentre la maggior parte delle altre componenti sono descritte da funzioni a zig-zag; inoltre, i testi che seguono il sistema A collocano l'equinozio primaverile a 10° di declinazione (nella costellazione dell'Ariete), mentre i testi del sistema B lo collocano a 8°.
Gran parte delle nostre conoscenze sull'astronomia lunare babilonese riguarda le effemeridi relative alle lune piene e nuove. Le eclissi sono calcolate con gli stessi metodi, e possono essere considerate il risultato di estrapolazioni compiute a partire dalle effemeridi. Alcune tavole si occupano esclusivamente della possibilità di eclissi, sia lunari che solari. Non deve stupire che questi estratti fossero elaborati soltanto dopo la compilazione delle tavole lunari. Esistono anche tavole di eclissi relative ad alcuni anni del V sec. a.C., ossia relative a un periodo anteriore alle effemeridi lunari a noi pervenute; queste prime tavole utilizzano procedimenti più semplici, non ancora compresi del tutto. Oltre ai testi delle effemeridi, anche per la Luna vi sono testi riguardanti le procedure di calcolo e un certo numero di tavole ausiliarie.
La diffusione dell'astronomia babilonese
di Francesca Rochberg
Durante il periodo ellenistico, la diffusione delle conoscenze astronomiche dalla Mesopotamia alla Grecia diede il primo impulso allo sviluppo dell'astronomia occidentale. Aspetti della tradizione astronomica babilonese furono acquisiti dall'astronomia e dall'astrologia ellenistiche e da qui confluirono nelle scienze delle tradizioni indiana, araba e dell'Europa medioevale. L'India recepì l'astronomia e l'astrologia occidentali sin dalla metà del II sec. d.C., ma l'impatto dell'astronomia indiana con quella araba si verificò nel IX sec. della nostra era, quando ormai la scienza indiana era un ibrido fra tradizione babilonese e greca. Gli astronomi arabi, oltre ad aver assorbito elementi babilonesi, giunti al mondo islamico attraverso il contributo indiano, erano anche direttamente debitori all'astronomia tolemaica dell'Almagesto greco. Questo trattato, in tutta la sua area di diffusione, rappresentò un importante veicolo di trasmissione dell'astronomia babilonese.
Le unità, i parametri e i metodi che costituiscono il corpo delle conoscenze astronomiche furono tramandate da Babilonia e incorporate nelle astronomie di queste più tarde scienze antiche e medioevali. Gli elementi principali della metrologia astronomica che si ritrovano nelle tradizioni successive sono il sistema sessagesimale, le unità di misura di tempo e di arco circolare, le unità di lunghezza e quelle della magnitudine delle eclissi in cubiti e dita, il giorno lunare e, infine, le coordinate eclittiche e la normalizzazione dello Zodiaco; a questi elementi si aggiungono i parametri numerici (sia in forma di relazioni di periodicità per i fenomeni lunari, solari e planetari, sia per quanto riguarda la durata della luminosità diurna), i metodi di calcolo delle tavole astronomiche noti come sistemi A e B e il metodo di calcolo dei tempi di levata delle costellazioni dello Zodiaco.
Metrologia astronomica
I calcoli di fenomeni astronomici nell'astronomia greca, araba e indiana erano eseguiti secondo il sistema di numerazione posizionale sessagesimale babilonese (v. cap. XI, Tav. IV). L'uso di questo sistema per le unità di misura di tempo, di angolo e di arco (v. cap. VI, Tav. III) passò nell'astronomia greca dalla metà del II sec. a.C. in connessione con Ipparco e Ipsicle (200 a.C. ca.). Per misurare le distanze angolari nel cielo (per es., tra le stelle fisse e il meridiano o tra i pianeti e le 'stelle normali', stelle di riferimento vicine all'eclittica), oltre alla magnitudine delle eclissi, erano utilizzate due unità di lunghezza, il cubito e il dito. Varie descrizioni attestano la conoscenza da parte dei Greci dei diari astronomici babilonesi e dei testi di osservazioni e di predizioni a essi connessi. Il cubito è usato in due delle più antiche osservazioni registrate nell'Almagesto di Tolomeo (II sec. d.C.), relative agli anni 244 a.C. e 236 a.C. (Almagesto, IX, 7). Tolomeo cita descrizioni babilonesi di eclissi che forniscono le seguenti informazioni: ora di inizio dell'eclissi, indicazione di totalità, ora in cui il fenomeno è al culmine, e, da ultimo, direzione e grandezza, in dita, del maggior momento di oscuramento. Egli cita anche le distanze in cubiti dalle stelle eclittiche all'alba per Mercurio, indicando le date secondo il calendario babilonese (v. cap. XII), in mesi lunari (tradotti in nomi di mesi del calendario macedone) e anni dell'era seleucide. Infine, Tolomeo riporta la distanza in dita da Saturno a una stella normale, di sera (Almagesto, IV, 6, 11; V, 14; VI, 9; IX, 7 e XI, 7). Il cubito babilonese è utilizzato anche da Strabone nella sua Geografia (II, 1, 18).
L'unità equivalente a 1/30 di un mese sinodico medio, ossia il giorno lunare (in sanscrito tithi), svolge un ruolo fondamentale nell'astronomia matematica babilonese. Le successioni di date delle effemeridi sono calcolate in tithi: un mese sinodico medio di 30 tithi, infatti, permette di calcolare le date senza dover fare riferimento ai giorni civili, il cui numero, in un calendario lunare, varia di mese in mese. Per i fenomeni planetari, il tithi sostituisce le date del calendario e permette la coordinazione tra l'avanzare in longitudine (numero dei gradi tra fenomeni consecutivi) e il tempo (numero di tithi tra fenomeni consecutivi). La più tarda astronomia indiana usava come unità 1/30 del mese lunare vero, reintroducendo in tal modo la variazione complessa nella durata del mese esclusa dal tithi babilonese.
Verso la metà del I millennio, l'eclittica, ossia il percorso del Sole e dei pianeti attraverso le stelle fisse (il 'sentiero' già individuato dagli antichi astronomi babilonesi) fu standardizzato come una fascia circolare nel cielo, costituita da 12 parti, o segni, di 30° ciascuna, poi detta Zodiaco e utilizzata come sistema di riferimento matematico in cui il percorso del Sole e dei pianeti potesse essere calcolato per mezzo di tali gradi (longitudine celeste). La più antica testimonianza diretta dell'esistenza dello Zodiaco risale ai diari astronomici cuneiformi del V sec. (Sachs 1988, n. 453 IV 2 e margine superiore 2-3, n. 440 v. 3', e n. 418: 5, 10, v. 8' e 14') e agli oroscopi (Rochberg 1998, testi 1 e 2, datati entrambi al 409 a.C.): in questi testi le posizioni dei pianeti sono indicate in relazione ai segni zodiacali o ai gradi all'interno di essi. Lo Zodiaco babilonese non era normalizzato secondo il punto vernale variabile, ma era siderale, vale a dire che il suo punto di riferimento era fissato in relazione alle stelle: come è stato già detto, Ariete 8° per il sistema B e Ariete 10° per il sistema A. Non si conosce la data, comunque precedente all'età ellenistica, in cui i Greci recepirono lo Zodiaco babilonese: i trattati di Autolico ed Euclide (300 a.C. ca.) presuppongono già l'eclittica e lo Zodiaco e, secondo un passo di Plinio (Naturalis historia, II, 31) il sistema fu introdotto in Grecia da Cleostrato intorno al 500 a.C. Nel I sec. d.C. è attestato l'uso dello Zodiaco in papiri astrologici greci e demotici; nell'Almagesto lo Zodiaco è normalizzato in Ariete 0°. Questo riflette la conoscenza della precessione degli equinozi e deriva, perciò, dall'uso babilonese. L'assimilazione del sistema babilonese di coordinate eclittiche permise di stabilire l'apparato numerico dell'astrologia dei decani egiziani e dei nakṣatra indiani (l'astrologia greca fece da tramite alla tradizione babilonese e cominciò a essere recepita attorno alla metà del II sec. d.C.).
Parametri numerici e metodi aritmetici
Fra le varie relazioni di periodicità babilonesi, l'esempio più antico è il ciclo lunisolare di 19 anni equivalente a 235 mesi sinodici, talvolta denominato 'ciclo metonico'. Questa relazione cominciò a essere utilizzata nel calendario babilonese intorno al 500 a.C., prima, quindi, della data di attribuzione a Metone di Atene (432 a.C.). Il grande astronomo Tolomeo di Alessandria accenna a un calcolo più antico relativo a un ciclo di 18 anni legato alle eclissi, il Saros, che egli definisce come 6585 giorni e 1/3=223 mesi sinodici=239 mesi anomalistici=242 mesi draconici=241 mesi siderali +(10 2/3)°=18 anni siderali +(10 2/3)°. Il sistema babilonese non dava la durata del periodo in giorni, né correggeva per longitudine, ma utilizzava per il calcolo delle possibilità delle eclissi, sia lunari che solari, cicli di 223 mesi (18 anni).
Tolomeo non riconosce i parametri lunari fondamentali di Ipparco come babilonesi: la loro origine mesopotamica è stata scoperta da Kugler. Molto probabilmente i parametri numerici babilonesi furono introdotti nell'astronomia greca da Ipparco: unendo l'aspetto empirico a quello teorico egli intendeva fornire una base quantitativa ai modelli cinematici della Luna e dei pianeti. Le relazioni di periodicità dei pianeti che Tolomeo attribuisce a Ipparco si basano sui periodi documentati nei cosiddetti 'pronostici per l'anno successivo' babilonesi: l'uso di questi periodi nell'astronomia e nell'astrologia greche dimostra ancora una volta l'influenza esercitata dall'astronomia babilonese sulla scienza ellenistica. Le relazioni di periodicità planetarie tratte dalle effemeridi babilonesi riappaiono anche nell'astronomia molto più tarda, in particolare nel capitolo XVII del Pañcasiddhāntikā di Varāhamihira, un'opera astronomica indiana del VI sec. d.C.
Il rapporto di 3:2 relativo alla durata del giorno (qui intesa come durata della luminosità diurna) nel giorno più lungo e in quello più corto ‒ usato nei calcoli babilonesi anche se non corrisponde alla reale latitudine geografica di Babilonia (v. sopra) ‒ fu adottato dai geografi greci. Poiché la durata del giorno più lungo aumenta in proporzione alla latitudine geografica, il rapporto tra il giorno più lungo e quello più corto indicherà la latitudine locale e, di conseguenza, la latitudine che i geografi greci assegnarono a Babilonia risulta sbagliata di parecchi gradi: questo errore causò nelle mappe antiche la deformazione della parte orientale del mondo allora conosciuto.
La grande diffusione della tradizione babilonese è illustrata dall'attestazione di schemi planetari babilonesi corrispondenti ai sistemi A e B (v. sopra) nell'astronomia greca successiva a Ipparco e in testi indiani e demotici. Per esempio, uno schema diagnostico del sistema A, in cui il moto sinodico di Marte è suddiviso in 6 zone dell'eclittica, compare nelle tavole Stobart, nell'Egitto di epoca romana. Queste tavole si basavano su metodi babilonesi, ma erano adattate per soddisfare le esigenze completamente diverse dell'astrologia ellenistica: vi erano catalogate le date degli ingressi dei pianeti nei segni zodiacali, invece delle date dei fenomeni sinodici come era uso nelle tavole babilonesi. Uno schema a sei zone relativo al moto sinodico di Marte, il trattamento dell'arco retrogrado di Marte e uno schema sul modello del sistema A per Mercurio sono attestati anche nel Pañcasiddhāntikā.
Alla base del periodo di eclisse attribuito a Ipparco (126.007 giorni) si trova il valore babilonese per il mese sinodico medio del sistema B (29;31.50.8.20 giorni) e la relazione di Ipparco a 251 mesi sinodici=269 mesi anomalistici è alla base delle colonne F (velocità lunare in gradi) e G (prima approssimazione della durata variabile del mese sinodico, presupponendo una velocità solare costante di 30° al mese) del sistema B (Kugler 1900). L'uso da parte di Ipparco di questi parametri lunari e della relazione periodica per il moto lunare in latitudine (5458 mesi sinodici=5923 mesi draconici) implica la conoscenza della relazione babilonese 1 anno =12;22.8 mesi sinodici. Inoltre, un frammento di un papiro greco proveniente dall'Egitto di epoca romana presenta una successione di numeri sessagesimali, i quali formano una funzione a zig-zag con parametri comuni alla colonna G delle effemeridi lunari del sistema B: questo testo dimostra come in questo periodo le effemeridi babilonesi fossero state riprodotte in greco e come la conoscenza della teoria lunare babilonese non si limitasse a isolate relazioni di periodicità o di osservazioni di eclissi (Neugebauer 1988).
Infine, per quanto riguarda i tempi di levata dello Zodiaco, i sistemi A e B facevano uso di due insiemi di tempi di levata per i dodici segni zodiacali in modo da formare progressioni aritmetiche in cui i valori estremi fossero nel rapporto 3:2 che era accettato come rapporto tra il giorno più lungo e quello più corto a Babilonia. Infatti, uno schema usato dai Babilonesi per il calcolo della durata della luminosità diurna si basava sull'idea che essa coincidesse con il tempo tra la levata eliaca e quella acronittica della costellazione zodiacale corrispondente alla metà dell'eclittica in un dato giorno dell'anno alla latitudine geografica di Babilonia (32,5° N). I tempi di levata dello Zodiaco furono adottati dai Greci per stabilire altre latitudini geografiche: Tolomeo fornisce una tavola con 10 diverse latitudini (Almagesto, II, 8). Il metodo babilonese per il calcolo dei tempi di levata si trova anche in Vettio Valente (150 d.C. ca.), nel Papiro Michigan 149 (II secolo d.C. ca.) e in Manilio. Come ha osservato Neugebauer:
L'importanza storica dello schema babilonese per i tempi di levata va molto oltre la loro applicazione alla teoria solare e lunare. Poiché la geografia matematica greca definiva la latitudine di una località in base alla durata massima della luminosità diurna M, il metodo babilonese utilizzato per trovare la funzione C(λ) della luminosità diurna in funzione della longitudine del Sole, fu opportunamente modificato, conservando però i sistemi aritmetici A o B per i tempi di levata. Il sistema geografico dei 'sette climi' conserva per gran parte del Medioevo tracce delle ascensioni oblique babilonesi. D'altro canto l'insieme dei tempi di levata babilonesi del sistema A si trova inalterato nell'astronomia indiana del VI sec. d.C., senza che sia presa in considerazione la posizione molto più meridionale dell'India. I tempi di levata e i modelli a essi collegati, che ebbero origine fondamentalmente in Mesopotamia, sono così diventati un eccellente indicatore dei contatti culturali. (Neugebauer 1975)
L'astrologia tardobabilonese: gli oroscopi
di Francesca Rochberg
Nel tentativo di superare l'imposizione di categorie moderne alla storiografia della scienza, nelle più recenti analisi dei testi della Mesopotamia antica si preferisce evitare l'uso dei termini astrologia e astronomia, intesi con le rispettive connotazioni moderne di pre- o pseudo-scienza e scienza. Si è mantenuto, tuttavia, un'utilizzazione strettamente descrittiva di tali termini: se il testo contiene predizioni è 'astrologico', altrimenti è 'astronomico'. Esiste un ulteriore problema terminologico nell'applicazione del termine 'astrologia' ‒ con il quale si sottintendono le teorie greche di epoca ellenistica ‒ al materiale babilonese, poiché quest'ultimo non condivide con l'astrologia greca basi cosmologiche o metodologiche comuni. Tuttavia, il termine astrologia può essere usato per indicare genericamente i presagi astrali e genetliaci mesopotamici e gli oroscopi babilonesi, differenziandoli comunque dalle astrologie greche più tarde, alcune delle quali rappresentano, peraltro, il retaggio dell'antica tradizione mesopotamica.
Non esistono equivalenti in accadico dei termini astrologia e astronomia. Tutti i testi babilonesi che riguardano l'indagine dei fenomeni celesti ‒ dai testi che sottopongono tali fenomeni a rigorose descrizioni matematiche a quelli che, sulla loro base, traggono previsioni sugli eventi umani ‒ rientrano nell'ambito di ciò che era chiamato ṭupšarrūtu Enūma Anu Enlil, "l'arte dello scriba della [serie dei presagi celesti] Enūma Anu Enlil" (v. cap. IV, par. 2). Se gli scribi babilonesi non distinguevano tra astrologia e astronomia intese in senso moderno, essi operavano, tuttavia, numerose distinzioni fra testi con interessi e obiettivi diversi, come si desume dalle intestazioni. La cultura mesopotamica era in grado di classificare e differenziare le parti di natura diversa di una scienza dei cieli articolata e coerente. Il profondo interesse che i Babilonesi nutrivano per i fenomeni celesti e per la possibilità di trarne pronostici durò fino alla fine della tradizione scribale cuneiforme: la raccolta di presagi celesti Enūma Anu Enlil continuò a essere copiata fino al periodo seleucide, l'ultimo oroscopo pervenutoci risale al 69 a.C. e l'ultimo testo astronomico è datato al 75 d.C.
Due aspetti caratteristici dell'astrologia tardobabilonese sono l'uso dello Zodiaco come sistema di riferimento per le posizioni degli astri e l'elaborazione di predizioni personali sulla base dei fenomeni celesti al momento della nascita. Questi elementi rappresentano una significativa deviazione dalla tradizione canonica della divinazione celeste babilonese, nota dalla serie dei presagi Enūma Anu Enlil, il cui interesse era strettamente pubblico, cioè relativo a questioni importanti per il re e lo Stato nel suo insieme. L'introduzione dello Zodiaco nel corso del V sec. portò con sé importanti cambiamenti nella tradizione classica dei presagi celesti. Il sistema di riferimento zodiacale fu ideato, probabilmente, in ambito astronomico piuttosto che astrologico: lo Zodiaco forniva, infatti, una comoda divisione matematica dell'eclittica in 12 parti di 30°, che serviva a calcolare l'avanzamento dei pianeti lungo l'eclittica stessa. Nei testi tardi, matematici e non, dai diari e le effemeridi fino agli oroscopi e ai presagi dei temi di natività, il riferirsi allo Zodiaco sostituì sistemi più antichi di determinazione delle posizioni degli astri, come le stelle nel 'sentiero della Luna'. Sembra probabile che i riferimenti ai segni zodiacali che si ritrovano nei testi di carattere astrologico provengano dai testi astronomici.
Tra il 600 e il 300 a.C. ca. l'astrologia si basò sempre più sull'astronomia e si sviluppò una branca di 'astrologia personale'. Il nuovo tipo di predizione personale basato sulla configurazione del cielo assunse due forme: i presagi dei temi di natività, formalmente connessi ai presagi celesti tradizionali, che fornivano predizioni per gli individui nati al momento del verificarsi di vari fenomeni astronomici; e altri testi, che non avevano la forma di presagi e che sono chiamati oroscopi, anche se non somigliano, se non superficialmente, agli oroscopi greci. L'oroscopia babilonese è una combinazione di tre tradizioni scribali: la tradizione della divinazione celeste, rappresentata dalla serie dei presagi Enūma Anu Enlil, che mantenne il suo interesse per le questioni pubbliche (re e Stato), la tradizione dei presagi sulle nascite, in cui queste assumevano una valenza mantica come un qualsiasi evento accaduto in un determinato mese e giorno, esattamente come nei menologi ed emerologi e, infine, la tradizione di divinazione personale rappresentata dalle serie fisiognomiche. In altre parole, l'oroscopo babilonese risulta da una miscela complessa di forme mantiche connesse fra loro: i presagi sulle nascite, quelli personali, quelli celesti e quelli dei temi di natività. Tuttavia, negli oroscopi babilonesi non sono incluse predizioni personali e di conseguenza il loro contenuto apparentemente risulta più astronomico che astrologico. Nei rari casi in cui compaiono delle predizioni, esse si presentano formalmente come le apodosi note dai presagi dei temi di natività; il loro interesse è generalmente rivolto all'avvenire della famiglia e della fortuna: "sarà privo di ricchezza", "i suoi giorni saranno lunghi", "avrà dei figli" o "avrà figli e figlie" (Rochberg 1998, pp. 50, 67, 80, 84). Poiché i dati astronomici sono forniti in relazione a data e ora di nascita dell'individuo, si può supporre che i fenomeni celesti registrati nel documento rappresentino segni importanti per la vita del neonato; il miglior supporto a quest'ipotesi è costituito proprio dai pochi paralleli tra le frasi in forma di apodosi degli oroscopi e i presagi dei temi di natività.
Tra la documentazione cuneiforme di carattere scientifico, gli oroscopi costituiscono una categoria distinta e abbastanza particolare di testi astrologici; essi ebbero origine nelle città di Babilonia e Uruk e furono prodotti nei periodi achemenide, seleucide e arsacide (V-I sec. a.C.). Nell'oroscopo è registrata la data e, talvolta, l'ora della nascita (un testo riporta la data del concepimento), seguita dalle posizioni della Luna, del Sole e di cinque pianeti e da ulteriori fenomeni astronomici connessi alla data di nascita (eclissi, equinozi o solstizi). Benché tutti gli oroscopi siano datati al momento della nascita di un individuo, la stesura dell'oroscopo non coincideva necessariamente con la data della nascita stessa, poiché i fenomeni astronomici registrati nel testo erano ottenuti con procedimenti di calcolo o a partire da dati contenuti in altri documenti. Le annotazioni sulla nascita, che registrano date e orari apparentemente allo scopo di trarne in seguito oroscopi, confermano che questi potessero essere preparati anche successivamente; inoltre il fatto che si estrapolassero dati da altri testi astronomici esclude ulteriormente la possibilità che gli oroscopi presentassero osservazioni, o anche calcoli, di fenomeni celesti al momento effettivo della nascita.
Il testo degli oroscopi (data e ora di nascita seguita da dati astronomici) non presenta una forma standard: alcuni dati sono prevedibili, ma, a parte un testo di cui è noto un duplicato, ogni oroscopo è unico e presenta problemi differenti di datazione e interpretazione. Il testo che segue, datato 12 (?) VII 92 dell'era seleucide, ossia 21 ottobre 219 a.C., è un esempio tipico:
Per mezzo del comando di Bel e B[eltiya possa andare bene]. Anno 92 [(era seleucide), Antioco (III) era re.] Tashritu 30, notte del 1[2(?), prima parte della notte, la Luna era] sotto 'la stella posteriore della testa dell'Uomo A Nolo [= α dell'Ariete]'. La Luna è passata 1/2 cubito a Est [di α dell'Ariete] […] il bambino è nato nella [sua] ora, [la luna era in Ariete(?),] il Sole era in Scorpione, Giove [era in Ariete], Venere e Saturno [erano] i[n Sagittario], Mercurio e Marte [tramontati non erano visibili.] Essi erano con il Sole. [Quel mese(?),] il tramonto della Luna dopo il sorgere del Sole è stato il 14, [l'ultima visibilità lunare prima del sorgere del Sole, il] 2[7.] [Il solstizio d'inverno è stato il 20 di Kislimu. Addaru, notte del 1[4 un'eclissi di Luna,] la totalità ha [avuto] luogo in Bilancia. Il giorno 28 un'ecl[issi di Sole] in Ariete, mezzo mese è trascorso [dall'eclissi precedente]. (Rochberg 1998, testo 14)
I dati principali raccolti negli oroscopi sono le longitudini dei pianeti Giove, Venere, Mercurio, Saturno, Marte, come anche quelle del Sole e della Luna; le longitudini sono date in generale con riferimento ai nomi dei segni zodiacali. I gradi di longitudine non sono frequenti, ma sono registrati in otto oroscopi, cinque dei quali provengono da Uruk. Un confronto tra le longitudini planetarie babilonesi e quelle calcolate secondo metodi moderni sulle date di questi otto oroscopi fornisce una prova evidente del grado di perfezionamento dei metodi babilonesi. Poiché il principale interesse è la data della nascita, i pianeti si trovano per lo più tra le apparizioni sinodiche. A eccezione di uno o due oroscopi del V sec., le apparizioni sinodiche sono menzionate solamente se, nel giorno della nascita, un pianeta occupa lo stesso segno zodiacale del Sole; soltanto raramente è indicata la data dell'apparizione sinodica, quando essa si verifica entro un giorno o due dalla nascita. Per quanto riguarda i fenomeni sinodici caratteristici, gli oroscopi s'interessano solamente alle prime e alle ultime visibilità; esempi attestati sono la prima e l'ultima visibilità di Mercurio come stella della sera e stella del mattino, e l'ultima visibilità di Venere, Marte e Saturno. Un'unica eccezione si riscontra nell'oroscopo più antico (V sec. a.C.), che registra date dei punti stazionari e di opposizione, e più precisamente il sorgere del pianeta Saturno al tramonto del Sole.
Oltre alle posizioni dei pianeti, sono regolarmente indicati altri eventi astronomici del mese o persino dell'anno in cui la nascita ha avuto luogo. Gli oroscopi provenienti da Babilonia registrano tre ulteriori fenomeni lunari, che sembrano essere considerati essenziali: se il mese precedente è stato pieno (30 giorni) o monco (29 giorni); la data dell'intervallo di tempo, attorno alla Luna piena e denominato na, tra il sorgere del Sole e il tramontare della Luna; infine, la data dell'intervallo di tempo, chiamato KUR, tra il sorgere della Luna e il sorgere del Sole nel giorno dell'ultima visibilità lunare. Poiché questi dati lunari non sono contenuti in nessuno degli oroscopi provenienti da Uruk, sembra che la tradizione di quest'ultima città fosse diversa. In tre oroscopi da Uruk si trovano indicazioni sulla latitudine lunare, usando tre termini tecnici: NIM, "latitudine positiva", SIG, "latitudine negativa" e MURUB4, "nodo" (tale terminologia è altrimenti nota soltanto dal vocabolario astronomico matematico tardo). Gli oroscopi registrano inoltre le eclissi, anche quando non coincidono con le date di nascita; tutte le eclissi registrate rappresentano predizioni e non osservazioni. La maggior parte degli oroscopi menziona le eclissi sia lunari sia solari, in particolare quelle che avvengono a distanza di mezzo mese l'una dall'altra (eclissi lunare a metà del mese, seguita da quella solare alla fine dello stesso mese), ed è indicato anche il segno zodiacale in cui l'eclissi è avvenuta. Infine, per lo più gli oroscopi comprendono anche la data del solstizio o dell'equinozio più vicino al momento della nascita.
Bibliografia
fonti
Al-Rawi 1991-92: Al-Rawi, Faruk - George, Andrew, Enūma Anu Enlil XIV and other early astronomical tables, "Archiv für Orientforschung", 38-39, 1991-1992, pp. 52-73.
Hunger 1989: Hunger, Hermann - Pingree, David, MUL.APIN. An astronomical compendium in cuneiform, Horn, Verlag Ferdinand Berger & Söhne Gesellschaft M.B.H., 1989.
‒ 1992: Astrological reports to Assyrian kings, edited by Hermann Hunger, Helsinki, Helsinki University Press, 1992.
Ipsicle: Hypsicles, Die Aufgangszeiten der Gestirne (Anaphorikos, polyglott), hrsg. und übersetzt von Vittorio de Falco und Max Krause, Göttingen, Vandenhoeck und Ruprecht, 1966.
Jones 1999: Jones, Alexander, Astronomical papyri from Oxyrhynchus, Philadelphia (Pa.), American Philosophical Society, 1999, 2 v.
Neugebauer 1942: Neugebauer, Otto, Egyptian planetary texts. On some astronomical papyri and related problems of ancient geography, Philadelphia (Pa.), American Philosophical Society, 1942.
‒ 1955: Neugebauer, Otto, Astronomical cuneiform texts. Babylonian ephemerides of the Seleucid period for the motion of the sun, the moon and the planets, London, Published for the Institute for Advanced Study; Princeton (N.J.), Lund Humphries, 1955, 3 v.
‒ 1988: Neugebauer, Otto, A Babylonian lunar ephemeris from Roman Egypt, in: A scientific humanist. Studies in memory of Abraham Sachs, edited by Erle Leichty, Maria de Jong Ellis and Pamela Gerardi, Philadelphia (Pa.), The University Museum, 1988, pp. 301-304.
Parpola 1970-83: Letters from Assyrian scholars to the kings Esarhaddon and Assurbanipal, compiled by Simo Parpola, Kevelaer, Butzon & Bercker, 1970-1983, 2 v.
Pinches 1955: Late Babylonian astronomical and related texts, copied by Theophilus G. Pinches and Johann N. Strassmaier, prepared for publication by A.J. Sachs, Providence (R.I.), Brown University Press, 1955.
Pingree 1988: Pingree, David - Walker, Christopher, A Babylonian star catalogue: BM 78161, in: A scientific humanist. Studies in memory of Abraham Sachs, edited by Erle Leichty, Maria de Jong Ellis and Pamela Gerardi, Philadelphia (Pa.), The University of Museum, 1988, pp. 313-322.
Reiner 1975: Babylonian planetary omens, by Erica Reiner, in collaboration with David Pingree, Malibu (Calif.), Undena Publications, 1975, 3 v.
Rochberg 1998: Rochberg, Francesca, Babylonian horoscopes, Philadelphia (Pa.), American Philosophical Society, 1998.
Sachs 1952a: Sachs, Abraham J., A late Babylonian star catalog, "Journal of Cuneiform Studies", 6, 1952, pp. 146-150.
‒ 1952b: Sachs, Abraham J., Babylonian horoscopes, "Journal of Cuneiform Studies", 6, 1952, pp. 49-75.
‒ 1988: Sachs, Abraham J., Astronomical diaries and related texts from Babylonia, completed and edited by Hermann Hunger, Wien, Verlag der Österreichischen Akademie der Wissenschaften, 1988-; 3 v.
Toomer 1984: Ptolemy's Almagest, translated and annotated by G.J. Toomer, New York-Berlin, Springer Verlag, 1984.
Varhamihira 1970-71: Varhamihira, Pancasiddhantika, edited and translated by Otto Neugebauer and David Pingree, Copenhagen, Munksgaard, 1970-1971, 2 v.
studi
Aaboe 1955-56: Aaboe, Asger, On the Babylonian origin of some Hipparchan parameters, "Centaurus", 4, 1955-1956, pp. 122-125.
‒ 1965: Aaboe, Asger, On period relations in Babylonian astronomy, "Centaurus", 10, 1965, pp. 213-231.
‒ 1991: Aaboe, Asger [et al.], Saros cycle dates and related Babylonian astronomical texts, Philadelphia (Pa.), American Philosophical Society, 1991.
‒ 1991: Aaboe, Asger, Babylonian mathematics, astrology, and astronomy, in: Cambridge ancient history, Cambridge-New York, Cambridge University Press, 1970-; v. III, 2: The Assyrian and Babylonian empires and other states of the Near East, from the eighth to the sixth centuries, 1991, pp. 276-292.
Bowen 1988: Bowen, Alan C. - Goldstein, Bernard R., Meton of Athens and astronomy in the late fifth century B.C., in: A scientific humanist. Studies in memory of Abraham Sachs, edited by Erle Leichty, Maria de Jong Ellis and Pamela Gerardi, Philadelphia (Pa.), The University Museum, 1988.
Britton 1996: Britton, John - Walker, Christopher, Astronomy and astrology in Mesopotamia, in: Astronomy before the telescope, edited by Christopher Walker, London, British Museum Press, 1996, pp. 42-67.
Brown 2000: Brown, David, Mesopotamian planetary astronomy-astrology, Philadelphia (Pa.), STYX, 2000.
Galter 1993: Galter, David, Die Rolle der Astronomie in den Kulturen Mesopotamiens, hrsg. von Hannes D. Galter, Graz, Kult, 1993.
Gössmann 1950: Planetarium Babylonicum, oder die sumerisch-babylonischen Stern-Namen, hrsg. von Felix Gössmann, Roma, Pontificio Istituto Biblico, 1950.
Koch-Westenholz 1995: Koch-Westenholz, Ulla, Mesopotamian astrology. An introduction to Babylonian and Assyrian celestial divination, Copenhagen, Museum Tusculanum Press, 1995.
Kugler 1900: Kugler, Franz X., Die babylonische Mondrechnung. Zwei Systeme der Chaldäer über den Lauf des Mondes und der Sonne, Freiburg im Breisgau, Herder, 1900.
‒ 1907-24: Kugler, Franz X., Sternkunde und Sterndienst in Babel, Münster in Westfalen, Aschendorff, 1907-1924, 2 v.
Neugebauer 1957: Neugebauer, Otto, The exact sciences in antiquity, 2. ed., Providence (R.I.), Brown University Press, 1957 (1. ed.: Copenhagen, E. Munksgaard; Princeton (N.J.), Princeton University Press, 1951; trad. it.: Le scienze esatte nell'antichità, Milano, Feltrinelli, 1974).
‒ 1975: Neugebauer, Otto, A history of ancient mathematical astronomy, Berlin-New York, Springer Verlag, 1975, 3 v.
‒ 1983: Neugebauer, Otto, Astronomy and history. Selected essays, New York-Berlin, Springer Verlag, 1983.
Pingree 1963: Pingree, David, Astronomy and astrology in India and Iran, "Isis", 54, 1963, pp. 229-246.
‒ 1982: Pingree, David, Mesopotamian astronomy and astral omens in other civilizations, "Berliner Beiträge zum Vorderen Orient", 1, 1982, pp. 613-631.
Rochberg 1988: Rochberg, Francesca, Aspects of Babylonian celestial divination. The lunar eclipse tablets of Enuma Anu Enlil, Horn, Verlag F. Berger, 1988.
‒ 1998: Rochberg, Francesca, Babylonian horoscopes, Philadelphia (Pa.), American Philosophical Society, 1998.
‒ 1999: Rochberg, Francesca, Babylonian horoscopy. The texts and their relations, in: Ancient astronomy and celestial divination, edited by Noel M. Swerdlow, Cambridge (Mass.), MIT Press, 1999.
Sachs 1948: Sachs, Abraham J., A classification of the Babylonian astronomical tablets of the Seleucid period, "Journal of Cuneiform Studies", 2, 1948, pp. 271-290.
Schiaparelli 1925: Schiaparelli, Giovanni, Scritti sulla storia della astronomia antica, Bologna, Zanichelli, 1925, 2 v.
Toomer 1988: Toomer, G.J., Hipparchus and Babylonian astronomy, in: A scientific humanist. Studies in memory of Abraham Sachs, edited by Erle Leichty, Maria de J. Ellis and Pamela Gerardi, Philadelphia (Pa.), The University Museum, 1988, pp. 353-362.
van der Waerden 1974: Waerden, Barthel L. van der, Science awakening, Groningen, Wolters Noordhoff, 1969-1974, 2 v.; v. II: The birth of astronomy, Leiden, Noordhoff, 1974.
Weidner 1957-71: Weidner, Ernst, Fixsterne, in: Reallexikon der Assyriologie, hrsg. von Erich Ebeling und Bruno Meissner, Berlin-New York, W. de Gruyter, 1928-; v. III, 1957-1971, pp. 72-82.