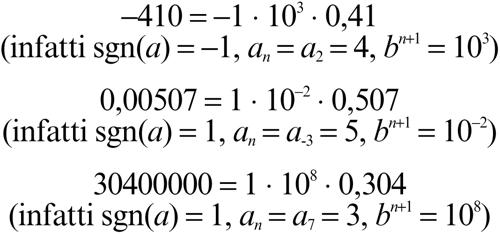virgola mobile

virgola mobile

virgola mobile o floating point, particolare rappresentazione dei numeri razionali in un automa esecutore che mette in evidenza l’ordine di grandezza del numero stesso. Stabilita la base b del sistema di numerazione scelto (nell’aritmetica ordinaria b = 10, nell’aritmetica elementare dei calcolatori b = 2), il numero a = a_na_n−1 ... a₁a₀, a₋₁ ... a_−k è considerato nella forma

dove sgn(a) fornisce il segno di a, a_i sono le sue cifre decimali, a_n la prima tra esse che è diversa da 0, b è la base della rappresentazione. Così, per esempio, considerando la base 10, i numeri seguenti sono riscritti in virgola mobile:

Senza la convenzione di scegliere a_n ≠ 0, ossia di considerare come a_n la prima cifra diversa da 0, la notazione in virgola mobile non sarebbe univoca, perché sarebbe possibile collocare la virgola (o il punto decimale) arbitrariamente. Con la convenzione adottata la rappresentazione in virgola mobile è detta normalizzata. In sintesi, la rappresentazione del numero

è del tipo:

dove b è la base numerica di rappresentazione (10 nell’ordinaria numerazione decimale), sgn(a) il segno del numero, E è l’esponente della base b (che, riscrivendo il numero in forma standardizzata, risulta essere n + 1) e M la mantissa (di n + k + 1 cifre significative in base b).

La rappresentazione in virgola mobile ha una stretta relazione con la → notazione esponenziale (si vedano i lemmi → aritmetica in virgola mobile o fissa; → floating point; → sistema di numerazione posizionale).