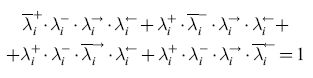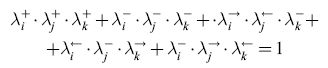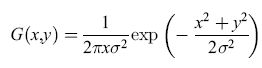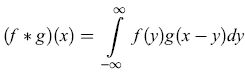Visione artificiale
Visione artificiale
La visione artificiale, lontana dall'essere una restrizione all'ambito visivo di tecniche e strumenti concettuali dell'intelligenza artificiale, si è da questa differenziata fin dagli anni Sessanta. Infatti, la sua attenzione si è focalizzata, piuttosto che sull'aspetto logico e simbolico della soluzione di problemi visivi, sullo sviluppo di metodi per estrarre informazione da immagini del mondo reale. In questo saggio discuteremo metodi e tecniche della disciplina attraverso l'analisi di un singolo problema significativo, quello della ricostruzione della struttura tridimensionale di una scena della quale è disponibile una singola immagine. Si tratta di un problema classico e complesso della visione artificiale, la cui soluzione completa ha fino a oggi eluso gli sforzi della comunità scientifica. Allo stesso tempo, si tratta di uno dei problemi che ha raggiunto i risultati teorici e pratici più interessanti.
Introduzione
La visione artificiale ha come obiettivo lo sviluppo di metodi che consentano a una macchina di comprendere ed elaborare l'informazione contenuta in una o più immagini. Questa disciplina si è sviluppata a partire dagli anni Sessanta in parallelo all'intelligenza artificiale, la disciplina che studia, più in generale, sistemi automatici in grado di svolgere compiti 'intelligenti', senza limitarsi ai processi di visione. A dispetto di queste poche parole di definizione, che possono far sembrare la visione artificiale come un particolare caso, legato all'ambito visivo, dei metodi dell'intelligenza artificiale, è senza dubbio interessante notare che tra le due discipline esistono notevoli differenze metodologiche.
Nell'intelligenza artificiale l'accento della ricerca è posto sull'aspetto logico e simbolico, e si dà spesso per assunta l'esistenza di sistemi in grado di estrarre dal mondo reale una rappresentazione simbolica che possa essere utilizzata da algoritmi di manipolazione delle informazioni e da sistemi inferenziali in grado di fare affermazioni e ragionamenti sulla struttura logica e geometrica del mondo rappresentato. Nella visione artificiale, una parte preponderante della ricerca è dedicata proprio al tentativo di estrarre tale rappresentazione simbolica da immagini del mondo reale. Il problema aperto più vivo e pressante della visione artificiale è forse proprio quello di costruire un ponte tra i risultati dell' elaborazione dell'informazione a basso livello di astrazione oggetto di indagine della cosiddetta early vision (livello precoce di elaborazione visiva), che può contare su tecniche ormai consolidate - e le elaborazioni su rappresentazioni simboliche dell'immagine. La costruzione di tali rappresentazioni simboliche, che includano una descrizione dell'immagine relativa agli oggetti e alle loro relazioni fisico-spaziali, è lo scopo della cosiddetta visione high level, cioè, ad alto livello di astrazione.
Dopo questo primo inquadramento metodologico, è interessante sottolineare come la visione artificiale si ponga obiettivi sia di carattere teorico che di carattere squisitamente applicativo. Tra gli obiettivi di carattere teorico vi è quello della costruzione di una teoria della visione per sistemi artificiali e biologici (Marr, 1982) e per aspetti particolari della visione, la costruzione di una teoria della segmentazione (Morel e Solimini, 1995) e di una teoria della percezione del moto (Verri et al., 1992). Tra i numerosi obiettivi di carattere applicativo citiamo la costruzione di sistemi robotici per l'ispezione e la manipolazione di oggetti e di sistemi per la guida automatica (Dickmanns et al., 1990) che hanno dimostrato la fattibilità della costruzione di un sistema di guida automatico per veicoli che viaggiano su autostrada. In questi ultimi anni, inoltre, hanno suscitato notevole interesse le applicazioni nel settore biomedico (Bizais et al., 1995) e le applicazioni relative all'analisi di documenti (O'Gorman e Kasturi, 1995) per quanto riguarda sia il riconoscimento ottico di caratteri che l'analisi della struttura della pagina.
Nonostante questi successi, la visione artificiale resta una disciplina non ancora matura, nella quale non esiste un'unica cornice teorica ben articolata e un corpus di problemi e tecniche che la comunità scientifica riconosce come fondamentali. Per quanto riguarda la cosiddetta early vision, è utile comunque distinguere almeno quattro diversi approcci possibili che hanno avuto notevole influenza sullo sviluppo della ricerca.
Il primo è l'approccio del riconoscimento di configurazione (pattern recognition), in cui i processi 'a basso livello' vengono studiati con un insieme di algoritmi ad hoc per estrarre diverse caratteristiche dell'immagine come, per esempio, i contorni degli oggetti (Pavlidis, 1982). Nonostante la mancanza di un'ispirazione comune, queste diverse tecniche sono un'acquisizione estremamente importante della visione artificiale e non si riscontra virtualmente problema di visione complesso (per esempio, il riconoscimento di oggetti) per la cui soluzione non si debba ricorrere, almeno in parte, a qualcuna di queste tecniche.
Il secondo tipo di approccio geometrico è quello in cui i problemi di visione artificiale vengono risolti mediante la geometria algebrica e la geometria proiettiva (Mundy e Zisserman, 1992; Faugeras, 1993); tale approccio è particolarmente efficace per affrontare problemi di calibrazione di telecamere e di stereovisione; inoltre, a un livello di astrazione più elevato, può essere usato per risolvere problemi di riconoscimento.
Un ulteriore approccio è quello chiamato variazionale (Blake e Zisserman, 1988), il quale considera diversi processi di visione come problemi di minimizzazione di un funzionale. Tra i vari problemi che si possono formulare in modo naturale in questa cornice vi sono quello dell' estrazione di contorni (v. oltre) e della suddivisione dell'immagine in regioni che risultano corrispondenti ai diversi oggetti (segmentazione).
Infine, vi è l'approccio statistico (Geman et al., 1990; Li, 1995) secondo cui l'immagine è modellizzabile come un processo stocastico che è possibile ricostruire con tecniche prese a prestito dalla meccanica statistica quali, per esempio, il rilassamento stocastico. Questo approccio ben si adatta a risolvere, tra gli altri, problemi di segmentazione e di restaurazione di un'immagine corrotta da rumore. Per quanto riguarda, invece, la visione high level, non è altrettanto facile isolare un numero ristretto di filoni di ricerca. Per ogni singolo problema significativo, come per esempio il problema del riconoscimento di oggetti (Jain e Flynn, 1993), esiste, infatti, una notevole varietà di tecniche disponibili che sono tipiche del problema e che non sono generalizzabili a una teoria complessiva della visione high level.
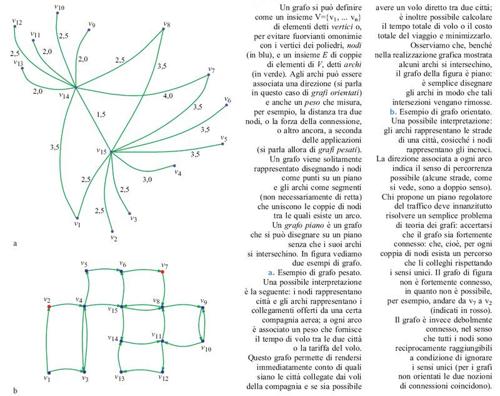
Tentare una rassegna esaustiva dei problemi di frontiera della visione artificiale sarebbe troppo ambizioso, anche per la mancanza di unitarietà di teorie, problemi e metodologie accennata precedentemente. È forse più utile, allora, analizzare una singola questione significativa e utilizzarla per illustrare alcuni problemi, tematiche e metodologie affrontate dalla disciplina. Nello specifico, analizzeremo il problema della ricostruzione automatica della struttura tridimensionale di una scena a partire da una singola immagine, per esempio una fotografia, utilizzando come sua rappresentazione schematica intermedia un line drawing, cioè un grafo piano (fig. 1) con segmenti di retta come archi. Si tratta di un problema classico di visione, di cui si può tracciare una storia non troppo dispersiva ma che allo stesso tempo coinvolge alcuni temi che sono tra i più importanti e ricorrenti della disciplina.
Comprendere una scena a partire da una singola immagine è qualcosa che gli esseri umani sanno fare a colpo d'occhio. Questa abilità si conserva virtualmente inalterata anche quando l'immagine non contiene informazioni di 'tessitura', ombreggiatura e colore, ma si riduce a un line drawing che rappresenta schematicamente l'immagine originale conservando solo la proiezione degli spigoli visibili degli oggetti che compongono la scena. l line drawing sono semplici da rappresentare ma l'analisi della configurazione geometrica tridimensionale che li ha generati non è banale; questo spiega la popolarità che hanno subito acquistato nella comunità scientifica e l'intensità con cui, a partire dagli anni Settanta, è stato studiato il problema della ricostruzione di una scena a partire da un line drawing. Nell'interpretazione automatica di immagini per mezzo di line drawing si trovano intrecciate visione e intelligenza artificiale; perciò questo saggio è diviso in due parti: nella prima affronteremo il problema dell'interpretazione dando per assunto che una rappresentazione simbolica - in questo caso, il line drawing - sia già disponibile; nella seconda parte, tratteremo, invece, la possibilità di ottenere tale rappresentazione a partire dall'immagine grezza e quali difficoltà comporti l'estrazione del line drawing.
L'interpretazione di un line drawing
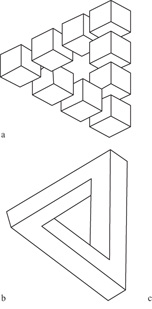
Fino agli anni Sessanta, fino cioè alla pubblicazione dei lavori di L.G. Roberts (1965), A. Guzman (1968) e vari altri autori, non era emerso un interesse degno di nota per gli aspetti 'computazionali' del problema dell'interpretazione tridimensionale di un line drawing, vale a dire per la formulazione di un metodo che permettesse di determinare se un disegno potesse essere la rappresentazione bidimensionale (tipicamente, la proiezione prospettica) di un oggetto fisico e, in caso affermativo, di determinarne una possibile realizzazione tridimensionale, possibilmente vicina a quella percepita istintivamente da un osservatore umano. Da molto tempo era comunque nota l'esistenza di figure impossibili, cioè di figure che non potevano corrispondere a nessun oggetto fisico: uno dei primi esempi si trova nell'Annunciazione di un pittore del 1500, trovata nella Grote Kerk di Breda (Paesi Bassi) nel 1902. Più di recente, nel 1934, il pittore Oscar Reutersviird scoprì il tribar (fig. 2) e diverse altre figure impossibili; l'ufficio postale svedese ha emesso nel 1980 una serie di francobolli dedicata a tali figure. Il tribar fu poi riscoperto (v. figura 2b) dal fisico-matematico oxoniense R. Pemose e da suo padre che, nel 1958, pubblicarono un lavoro sull'argomento. Maggiori dettagli e riferimenti bibliografici sulla storia della scoperta delle figure impossibili si possono trovare nell' articolo di E. Ernst (1986) da cui abbiamo tratto queste notizie essenziali. Il concetto di figura impossibile è stato ripreso ed elaborato artisticamente in varie forme da M.C. Escher nelle sue litografie, alle quali si deve probabilmente la notevole popolarità del concetto di figura impossibile. L'esistenza di figure impossibili è quindi ampiamente nota e non occorre insistervi. Meno noto è che esistono metodi automatici per stabilire se una figura è impossibile o se può essere considerata, al contrario, come la proiezione di un poliedro, o di una composizione di poliedri; se, in altri termini, la figura è 'realizzabile'.
A dare una svolta alla ricerca di un algoritrno per determinare se una figura è realizzabile sono stati probabilmente i contributi indipendenti di D.A. Huffrnan e M.E. Clowes nel 1971 (Sugihara, 1986) che nascono da una scuola di pensiero dominante dell'intelligenza artificiale di quegli anni, quella simbolista. Secondo questa scuola la costruzione di sistemi intelligenti doveva basarsi sull'elaborazione di metodi per la manipolazione di simboli e sullo sviluppo di sistemi inferenziali analoghi a quelli di grande successo del calcolo dei predicati e della logica simbolica in generale. Il titolo del lavoro di Huffman, Impossible objects as nonsense sentences (Oggetti impossibili visti come frasi prive di senso), evidenzia l'approccio linguistico-simbolico.
L'approccio linguistico all'etichettatura
L'idea fondamentale dei lavori di Huffrnan e Clowes è quella di associare al line drawing una 'frase', o per essere più specifici una proposizione booleana, che sia soddisfacibile se e solo se il line drawing è realizzabile. Per chi non ha familiarità con il calcolo proposizionale, conviene ricordare che una proposizione booleana è costruita a partire da un certo numero di variabili logiche Xl, ... Xn che possono assumere solo due valori, 0 e 1 ('falso' e 'vero'), e sulle quali sono ammesse le operazioni di negazione logica, rappresentata da una barra sulla variabile (x̄=1 se e solo se x=0), di somma logica (x+y=1 se e solo se x=1 oppure y=1) e di prodotto logico (x ∙ y = l se e solo se x=y= 1). Esempi di proposizioni booleane sono F =x1 ∙ (x̅2 +x1 ∙ x3) e F = (x̅1 + x2) ∙ (x1 + x̅2). La proposizione si dice soddisfacibile se e solo se esiste un assegnamento di valori 0 o 1 alle variabili x1, .. xn tale che la proposizione booleana valga 1. Per esempio F = x1 ∙ (x̅2 + x1 ∙ x3) può essere soddisfatta (tra gli altri) dall'assegnamento x1 = 1, x2 = 0, x3 = 0. Un esempio di proposizione non soddisfacibile è F = x1 ∙ x̅3 ∙ (x̅2 + x1 ∙ x3) ∙ (x2 + x̅1). Huffman e Clowes non realizzarono questo programma completamente, ma trovarono entrambi un'importante condizione necessaria per la realizzabilità di un line drawing come proiezione piana o prospettica di una scena poliedrica in termini della soddisfacibilità di una proposizione booleana. Questa condizione viene generalmente definita etichettabilità.
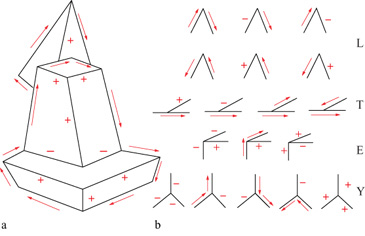
Etichettare un line drawing significa, intuitivamente parlando, assegnare a ogni segmento del line drawing un'etichetta che descriva alcune proprietà geometriche dello spigolo in tre dimensioni (3D) di cui il segmento è la proiezione bidimensionale (fig. 3): se si tratta, cioè, di uno spigolo originato da una discontinuità nell'orientazione della superficie (in questo caso si distingue ancora tra spigoli convessi (+) e concavi (-)) o da una discontinuità nella profondità (→).
Huffman e Clowes focalizzarono la loro attenzione alle scene triedriche, cioè alle scene composte di poliedri con tre facce piane che si incontrano esattamente in ogni vertice (v. figura 3a). Studiando sistematicamente il modo in cui i vertici triedrici vengono proiettati sul piano immagine a formare vertici bidimensionali - che chiameremo, per meglio distinguerle dalla loro controparte tridimensionale, giunzioni - essi trovarono conveniente distinguere le giunzioni in quattro tipi strutturalmente diversi (Y, E, L, T) e dimostrarono che per ognuno di questi tipi vi è un numero molto limitato di combinazioni di etichette che rendono la giunzione realizzabile come proiezione di un vertice 3D; tali combinazioni di etichette, dette etichettature legali, formano il cosiddetto catalogo di HujJmanClowes delle etichettature legali (v. figura 3b).
Un line drawing si dice etichettabile se e solo se è possibile assegnare a ogni segmento un'etichetta tale che ogni giunzione sia etichettata in accordo con il catalogo delle giunzioni. Il problema dell'etichettatura è quindi un problema combinatorio. Osserviamo che l'etichettatura dà una descrizione qualitativa della scena tridimensionale, e che essa è una forma di realizzabilità locale, in quanto un line drawing etichettato correttamente è realizzabile in corrispondenza delle sue giunzioni ma non necessariamente nel suo complesso.
Qui di seguito verrà considerato l'approccio linguistico al problema anche se la trattazione non corrisponde esattamente né a quella di Huffman né a quella di Clowes. Vengono introdotti quattro predicati booleani
per ogni segmento si(i = 1, ... ,n), tali che λi+ = l se e solo se Si è etichettato +; analogamente per λi-. Per quanto riguarda λi→ e λi← supponiamo che ogni segmento sia identificato da una coppia di vertici: Si = (VI, V2). Poniamo λi→ = 1 (rispettivamente, λi← = 1) se e solo se Si è etichettato con una freccia che va da VI a V2 (rispettivamente, da V2 a VI) cioè se e solo se Si è orientato in maniera concorde o discorde rispetto alla direzione intrinseca del segmento. I quattro predicati devono soddisfare la seguente equazione, che assicura che esattamente uno dei predicati è vero per ogni segmento:
formula [
l]
Ogni etichettatura legale di una giunzione corrisponde a un insieme di valori per i predicati associati ai segmenti della giunzione. Questo insieme di valori può essere descritto per mezzo di un'equazione booleana. Per fare un esempio, l'equazione
formula [2]
deve essere soddisfatta dai segmenti incidenti Si, Sj' sk (ordinati in senso antiorario) di una giunzione a Y, per la quale viene assunto, per chiarezza, che la direzione intrinseca dei segmenti incidenti sia quella uscente dal centro della giunzione. Che questa sia effettivamente l'equazione associata a una giunzione a Y si può facilmente verificare mediante un confronto diretto con il catalogo di Huffrnan-Clowes (v. figura 3b).
Abbiamo ora un'equazione per ogni segmento e un'equazione o equazioni simili tra loro per ogni giunzione. Combinando queste equazioni otteniamo una proposizione booleana che è soddisfacibile se e solo se il line drawing è etichettabile. Si è così ridotto il problema dell'etichettatura al problema della soddisfacibilità di un'espressione booleana. Osserviamo che questo è un metodo poco efficiente di riduzione del problema, in quanto tutti i metodi che tentano di risolvere il problema della soddisfacibilità impiegano, in generale, un numero di passi che cresce esponenzialmente con la lunghezza della proposizione booleana. Su questi aspetti di efficienza torneremo con maggiore dettaglio in seguito, quando discuteremo della complessità degli algoritmi di interpretazione dei line drawing.
Etichettatura come problema di soddisfacimento di vincoli
Il lavoro di Huffman e Clowes è stato esteso in numerose altre direzioni, nel tentativo di trattare classi di scene più vaste o di trovare metodi più efficienti per risolvere il problema dell'etichettatura. Tra i vari lavori di questo genere, particolarmente influente è stato quello di D. Waltz (1975), che ha studiato l' etichettatura di line drawing di scene triedriche con la presenza di ombre e fenditure, sviluppando per l'etichettatura un algoritrno di filtraggio per il quale venivano riportate ottime prestazioni.
Nell'approccio di Waltz, l'etichettatura viene realizzata con una procedura di esplorazione di un grafo mediante una ricerca all'indietro (backtracking) delle giunzioni del line drawing, preceduta da una fase di filtraggio in cui viene realizzata una sorta di 'coerenza locale'. Data una giunzione, vengono rimosse tutte le etichettature che sarebbero a priori permesse dal catalogo di Huffman-Clowes ma per le quali non esiste un'etichettatura delle giunzioni vicine che sia con essa compatibile. La procedura viene ripetuta per tutte le giunzioni e ricorsivamente su tutto il grafo fino a quando non è più possibile rimuovere altre etichettature.
Il lavoro sui line drawing, in special modo l'approccio elaborato da Waltz, ha indotto l'analisi di un problema più generale, quello del soddisfacimento di vincoli (CSP, Constraint Satisfaction Problem), che è diventato uno dei problemi più popolari dell'intelligenza artificiale grazie alla sua capacità di modellizzare numerose situazioni in cui è necessario rendere compatibile l'informazione che deriva da diverse fonti (Mackworth e Freuder, 1993). Possiamo formularIo in questo modo: è dato un insieme di variabili X1, ... Xn, ognuna delle quali può assumere un insieme finito di valori, ed è dato un insieme di relazioni del tipo "il valore a della variabile Xi è compatibile con il valore b della variabile Xj". Il problema è quello di trovare un insieme di valori delle variabili che soddisfi tutti i vincoli. Analogamente al problema della soddisfacibilità di una proposizione booleana, non si conoscono metodi di soluzione efficienti (cioè, di complessità polinomiale nel caso peggiore, secondo l'usuale identificazione a cui accenneremo di nuovo più avanti), ed è verosimile che non ne esistano. L'approccio più popolare resta comunque quello di Waltz, e numerosi sforzi sono stati fatti per sviluppare metodi sempre più sofisticati di esplorazione di grafi con backtracking e per migliorare il filtraggio preliminare.
Nel suo lavoro, Waltz riportava sei esempi diversi di line drawing e il numero di passi che l'algoritrno impiegava a etichettarIi; da questi deduceva che il numero di passi impiegati dall'algoritmo stesso era all'incirca proporzionale al numero di segmenti del line drawing. Al di là del fatto che la conclusione era basata su un campione molto piccolo, la ragione di questo comportamento lineare era probabilmente dovuta al filtraggio preliminare di Waltz che determina, in effetti, complessità lineare nel numero di giunzioni e di segmenti; inoltre, si verifica spesso il caso in cui alla fine della procedura di filtraggio solo un numero esiguo di segmenti non sono etichettati in modo unico. Anche questo approccio all'etichettatura, però, richiede nei casi più difficili un tempo che cresce esponenzialmente con la complessità.
L'approccio di Sugihara alla realizzabilità
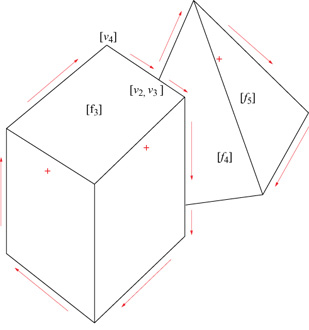
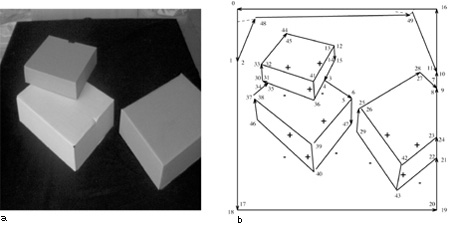
L'etichettabilità rappresenta, come fu chiaro fm dall'inizio, una condizione necessaria ma non sufficiente per la realizzabilità di un line drawing. Molte altre condizioni necessarie furono affiancate all'etichettabilità: una delle più interessanti è probabilmente l'esistenza di una figura duale nello spazio gradiente, uno strumento matematico introdotto da A.K. Mackworth nel 1973 . Il formalismo dello spazio gradiente, anche in versioni più sofisticate di quella introdotta da Mackworth, si rivelò però insufficiente per decidere la realizzabilità di un line drawing, e cominciò a farsi strada l'idea che una soluzione completa potesse essere trovata solo nel contesto della programmazione lineare. A conferma di questa previsione, la soluzione cercata fu trovata nel 1982 da K. Sugihara (1986), che ridusse il problema della realizzabilità di un line drawing etichettato a un problema di programmazione lineare. L'osservazione chiave è che è possibile associare a un line drawing etichettato un sistema di equazioni e disequazioni lineari le cui soluzioni, se esistono, corrispondono alle possibili realizzazioni tridimensionali del line drawing stesso. Non entreremo nei dettagli formali di come sia possibile costruire il sistema lineare associato al line drawing etichettato, ma daremo un'idea del procedimento servendoci di un esempio, riportato in figura (fig. 4).
A ogni giunzione dell'immagine vengono associati uno o più vertici della scena 3D (i vertici associati sono più di uno se alla giunzione afferiscono segmenti occlusivi). A ogni vertice vi corrisponde una tema di coordinate (xi,yi,zi). Nel caso in cui il line drawing sia proiezione ortografica della scena, le coordinate xi e yi si mantengono inalterate nell'immagine e sono quindi note, mentre la coordinata zi è incognita. Così, per esempio, alla giunzione indicata con [νi] nella figura 4 corrisponde il vertice vi = (x1 ,y1,z1) per il quale zi è l'unica incognita; alla giunzione indicata con [ν2,ν3] della stessa figura corrispondono due vertici ν2 e ν3 di cui uno (supponiamo che sia ν2) appartiene all'oggetto più vicino all'osservatore e il terzo (ν3) appartiene all'oggetto più lontano dall'osservatore (in quest'ultimo caso non si tratta di un vero vertice poliedrico ma semplicemente di un punto appartenente a uno spigolo del poliedro parzialmente occluso).
A ogni poligono [fj] dell'immagine viene associata una faccia pianafì della scena, giacente su un piano di equazione ajx + bjy + z + cj = 0. Questa equazione descrive un piano non perpendicolare al piano immagine (tale situazione non è ammessa) e i coefficienti aj,bj,cj sono incogniti.
Se in base all'etichettatura disponibile è possibile dire che il vertice νi = (xi,yi,zi) appartiene alla faccia fj (di equazione ajx+bjy+z+cj=0), allora si aggiunge al sistema l'equazione:
ajxi + bjyi + zi + cj = 0, [3]
dove le incognite sono, naturalmente, aj,bj,cj,zi. Nell'immagine della figura 4, il vertice νI è l'intersezione di tre facce piane f1,f2,f3 e perciò appartiene contemporaneamente a tutte e tre le facce. Di conseguenza, valgono le tre equazioni ajx1 +bjy1 +z1 +cj=0 (j = 1,2,3). Se in base all'etichettatura è possibile dire che il vertice νi = (xi,yi,zi) è dietro alla faccia fj, intendendo con ciò che νi e il centro di proiezione sono situati su parti opposte rispetto al piano che contiene la faccia fj, allora si aggiunge al sistema la disequazione:
ajxi+bjyi+zi+cj > 0 [4]
Come esempio, consideriamo il vertice ν4 della figura 4: le facce.f3 e f1 si incontrano in uno spigolo convesso (+), e il vertice giace sulla faccia.f3; perciò, esso è dietro la faccia f1, e vale l'equazione a1x4+b1y4+z4+c1 > 0. Se in base all'etichettatura è possibile dire che il vertice νi = (xi,yi,zi) è davanti al vertice νh = (xi,yi,zh) di uguale proiezione sul piano immagine, aggiungiamo al sistema la disequazione:
zi ≤ zh.
Per esempio, i vertici ν2 = (x2,y2,z3) e ν3 = (x2,y2,z3) nella figura 4 sono proiettati nello stesso punto del piano immagine, [ν2, ν3], e ν2 è situato davanti a ν3, per cui si può dire che z2≤z3.
Raccogliendo tutte le equazioni e le disequazioni si ottiene un sistema le cui incognite sono le coordinate z dei vertici introdotti e i coefficienti a, b, c dei piani corrispondenti ai vari poligoni. Osserviamo che, benché il sistema così costruito contenga disuguaglianze forti (cioè che non comprendono la possibilità dell'uguaglianza), come mostra per esempio l'equazione [4], può essere ridotto facilmente a un sistema in cui tutte le disuguaglianze sono deboli, cioè con la possibilità dell'uguaglianza (Sugihara, 1986). Tale condizione è necessaria per applicare i metodi di programmazione lineare. Se il sistema di equazioni e disequazioni ha soluzione, il line drawing etichettato rappresenta correttamente una scena poliedrica.
Nonostante che il metodo di Sugihara per affrontare il problema della realizzabilità di un line drawing rappresenti una soluzione completa, tale approccio soffre di gravi instabilità numeriche. Se, infatti, le equazioni [3] sono ridondanti, la realizzabilità dipende in modo critico dalla posizione delle giunzioni; una piccola perturbazione di tale posizione è sufficiente per rendere il line drawing irrealizzabile e, di conseguenza, l'applicazione del metodo diventa priva di significato. Sugihara era ben consapevole di ciò e, per ovviare al problema di instabilità numerica, ha proposto un meccanismo adatto a correggere la posizione delle giunzioni nell'immagine in modo da rendere tra loro compatibili, quando possibile, le eventuali equazioni ridondanti (Sugihara, 1986). Il difetto di questo meccanismo di correzione degli errori sulla posizione delle giunzioni, nel quale non ci addentriamo, è che risulta oneroso da un punto di vista computazionale.
La complessità dell'interpretazione dei line drawing
La procedura ideata da Sugihara è l'ultimo tassello per la costruzione di una strategia che consenta, dato un line drawing, di trovare una sua possibile 'realizzazione' come scena poliedrica o di concludere che si è di fronte a una figura impossibile. La strategia può essere così riassunta: si studia l'etichettabilità del line drawing. Se l'immagine non è etichettabile, si conclude che il line drawing rappresenta una figura impossibile. Nel caso in cui l'immagine sia etichettabile, invece, si trova un'etichettatura particolare del line drawing e successivamente, mediante la procedura di Sugihara, si controlla se l'immagine etichettata è realizzabile e, se lo è, si trova una particolare realizzazione; in caso contrario, si scarta l'etichettatura e se ne prova un'altra. Se le etichettature possibili vengono esaurite senza che si sia trovata un'etichettatura con la quale il line drawing è realizzabile, l'immagine rappresenta una figura impossibile.
La strategia delineata sopra è una soluzione completa al problema dell'interpretazione di un line drawing. Si tratta di un modo di risolvere il problema praticabile, o l'onere computazionale è tale da renderla puramente una soluzione di principio? E in quest'ultimo caso, esistono strategie più efficienti? Queste sono domande classiche che ci si pone per ogni problema di calcolo, e che sono dominio della teoria della complessità. L'analisi di complessità è parte essenziale dell'analisi di un problema di visione (Tsotsos, 1990).
Prima di rispondere a queste domande, è interessante fare qualche considerazione introduttiva sul concetto di complessità. La complessità di un algoritmo è il numero di passi T(n) che l'algoritrno impiega nel caso peggiore per risolvere il problema, in funzione della dimensione n dei dati in ingresso. Per fare un esempio, consideriamo il problema di stabilire se un numero N espresso in base lO è divisibile per tre. La dimensione dei dati di ingresso è il numero n di cifre di N, che è approssimativamente n≈log10N. Un semplice algoritmo per stabilire la divisibilità per tre è quello di calcolare la somma modulo 3 delle n cifre (ricordiamo che se a e b sono due numeri naturali, la loro somma modulo 3 è il resto della divisione intera di a + b per 3): questa somma è uguale a zero se il numero N è divisibile per tre. La complessità di tale algoritrno è lineare, nel numero delle cifre: T(n) è un numero di ordine n. Più in generale, si dice che la complessità di un algoritmo è T(n) = O(f (n)) se esiste una costante c tale che T(n) ≤ c ∙ f (n) per tutti i numeri interi n.
La complessità di un problema si può identificare con la complessità dell'algoritmo 'migliore' - cioè, più efficiente asintoticamente - che risolve il problema. Si tratta ovviamente di un oggetto difficile da calcolare. Un problema si considera trattabile o, in altri termini, risolvibile in modo efficiente, se e solo se la sua complessità T(n) è una funzione al più polinomiale della dimensione n dei dati di ingresso. Per molti problemi si conoscono solo algoritmi di complessità esponenziale, o comunque non polinomiale: un esempio è il cosiddetto problema della soddisfacibilità di una formula booleana, introdotto precedentemente; un altro esempio è il cosiddetto problema del commesso viaggiatore, che consiste nel determinare, dato un insieme di città e di distanze tra coppie di città, se esiste un percorso che passi per tutte le città e che abbia un chilometraggio inferiore a una certa soglia. Come accennavamo prima, è difficile stabilire limiti inferiori per la complessità di un problema; è talvolta possibile però dimostrare che un problema appartiene alla classe dei problemi NP-completi (che comprende, tra gli altri, i due problemi citati sopra) che si pensa formata da problemi di complessità esponenziale sostanzialmente isomorfi tra loro. I problemi NP-completi si chiamano così perché appartengono alla classe dei problemi NP (Non deterministic Polynomial): la classe NP comprende tutti i problemi che non si riescono a risolvere con complessità polinomiale ma che sono verificabili polinomialmente. Data cioè una proposta di soluzione, è possibile stabilire con complessità polinomiale se questa è effettivamente una soluzione del problema. Per esempio, il problema del commesso viaggiatore appartiene alla classe NP perché è possibile verificare con una semplice somma (che evidentemente ha complessità polinomiale) se un dato percorso che tocca tutte le città ha un chilometraggio inferiore alla soglia assegnata. I problemi NP-completi, inoltre, si chiamano così perché sono completi per la classe NP. Un problema X si dice completo per una classe C se ogni problema appartenente a C si può trasformare in X con complessità polinomiale. In altri termini, nessun problema in C è 'più difficile' di X. Se esiste un algoritrno che risolve X con complessità O(T(N)), questo stesso algoritmo si può usare per risolvere un qualsiasi altro problema Y in C con complessità O(T(N) + p(N)), dove O(P(N)) è la complessità dell'algoritmo che trasforma X in Y. Per questa ragione, se per un problema NP-completo qualsiasi venisse trovata una soluzione di complessità polinomiale, questa sarebbe immediatamente traducibile in una soluzione di complessità polinomiale per tutti gli altri problemi NP-completi e, più in generale, per tutti i problemi della classe NP.
Il problema di stabilire se i problemi NP-completi sono effettivamente di complessità non polinomiale - come la maggior parte degli esperti sospettano - è un problema aperto di notevole importanza (per molti, il problema aperto dell'informatica teorica). Molti sforzi sono stati dedicati alla soluzione di questo problema fin dall'introduzione del concetto di NP-completezza, a opera di S.A. Cook nel 1971. I problemi NP-completi sono reciprocamente legati dal fatto che se per uno di essi venisse trovata una soluzione di complessità polinomiale, questa sarebbe immediatamente traducibile in una soluzione di complessità polinomiale per ognuno di essi. Senza addentrarci in questi dettagli, rimandiamo il lettore interessato a uno dei testi classici della disciplina, il libro di M.R. Gareye D.S. Johnson (1979). Intuitivamente, ci si aspetta che la complessità dell'interpretazione di un line drawing sia polinomiale nella dimensione n dei dati in ingresso, nel caso specifico il numero di segmenti o di giunzioni. Il cervello umano è infatti in grado di afferrare all'istante la struttura 3D di un line drawing, e questo sembra indicare l'esistenza di un algoritmo efficiente. A dispetto di questa intuizione, i risultati che sono stati trovati sulla complessità dell'interpretazione di scene sono soprattutto negativi.
Prima di enunciare questi risultati, diamo uno sguardo alla complessità della strategia interpretativa riassunta all'inizio di questo paragrafo. In questa strategia vi sono due difficoltà. La prima viene dall' etichettatura: tutti gli algoritmi conosciuti (compreso quello di Waltz) per verificare l'etichettabilità e trovare un'etichettatura sono di complessità esponenziale nel numero di giunzioni e segmenti del line drawing. La seconda è che anche il numero di etichettature valide da sottoporre al vaglio dell'algoritmo di realizzabilità di Sugihara - che è, di per sé, di complessità polinomiale cresce esponenzialmente con il numero di segmenti.
La strategia è, perciò, altamente inefficiente. Il problema della realizzabilità è effettivamente intrattabile, o stiamo solo adottando l'approccio sbagliato? A priori si può pensare di risolvere la prima difficoltà cercando algoritmi di etichettatura migliori, nella speranza di trovarne uno di complessità polinomiale. Anche se questa iniziativa avesse successo, la strategia resterebbe di complessità esponenziale perché esponenziale è il numero di etichettature possibili, e questa difficoltà è insormontabile (è facile infatti produrre esempi di line drawing realizzabili che hanno un numero esponenziale di etichettature). L'unica via di uscita sarebbe quindi quella di cercare una strategia alternativa che, per determinare la realizzabilità di un line drawing, non passi per lo stadio di etichettatura. L.M. Kirousis e C.H. Papadimitriou (1988) dimostrarono, però, che sia la ricerca di un algoritmo di etichettatura che quella di un approccio alternativo alla realizzabilità efficienti sono presumibilmente destinate al fallimento, in quanto entrambi questi problemi sono NPcompleti anche per il caso di scene triedriche. La dimostrazione avviene mediante la riduzione del problema della so ddisfacibilità di una proposizione booleana al problema dell'etichettabilità-realizzabilità: viene cioè fornito un metodo di complessità polinomiale che trasforma una proposizione booleana arbitraria in un line drawing che è etichettabilerealizzabile se e solo se la proposizione booleana è soddisfacibile. Siccome il problema della soddisfacibilità di una proposizione booleana è NP-completo, questo dimostra che il problema di etichettabilità-realizzabilità è almeno tanto difficile quanto il problema della soddisfacibilità ed è quindi anch'esso NP-completo. Osserviamo che questa riduzione è l'aspetto duale dell'approccio linguistico di Huffman e Clowes all'etichettabilità, con il quale si riduce il problema dell' etichettabilità a una proposizione booleana. Il risultato di Kirousis e Papadimitriou dimostra che è possibile fare anche il contrario con complessità polinomiale.
Nelle pagine precedenti abbiamo visto come il problema della ricostruzione della struttura 3D di una scena poliedrica a partire da un line drawing sia NP-completo e sia, perciò, presumibilmente intrattabile. Questo risultato contrasta con la facilità con la quale il cervello riesce a interpretare un line drawing, e questo contrasto è da spiegare. Nella teoria della complessità emergono alcune domande classiche, per comprendere meglio la struttura di un problema NP-completo e svilupparne algoritmi con prestazioni buone almeno in casi particolari. È importante porsi queste domande anche nel caso del problema della ricostruzione di strutture 3D e studiarne le implicazioni per la visione artificiale e biologica. La prima questione è se la complessità del caso peggiore rifletta la complessità tipica del problema o se le situazioni peggiori siano anomalie di scarso interesse. Inoltre, qual è la complessità media del problema?
Un'altra domanda è se esistono casi particolarmente significativi in cui la NP-completezza viene infranta.
Il problema della complessità media è molto delicato e non esistono stime teoriche. In uno studio recente (Parodi et al., 1996) tale problema è stato affrontato da un punto di vista sperimentale: campioni di line drawing vengono generati come proiezioni di poliedri casuali. In questo caso la risposta al problema della realizzabilità è sempre affermativa, perché sappiamo a priori che il line drawing è proiezione di un poliedro e quello che interessa è produrre esplicitamente un'interpretazione. Questo problema è naturalmente più vicino a quello che il cervello umano è abituato a risolvere. Gli esperimenti mostrano che la complessità tipica del problema dell'etichettabilità cresce linearmente con il numero di segmenti, ed è quindi drasticamente più bassa di quella del caso peggiore. Va sottolineato che questi risultati non danno immediatamente informazioni sul problema dell'interpretazione di un line drawing di una scena naturale, in quanto è difficile costruire un modello della distribuzione statistica delle scene naturali nell'insieme di tutte le scene poliedriche.
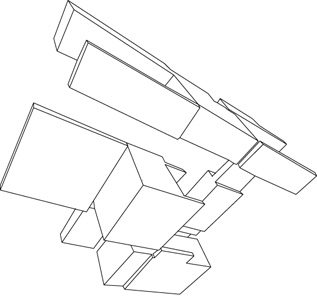
Per quanto riguarda la ricerca di casi speciali significativi, nello stesso lavoro in cui hanno dimostrato la NP-completezza del problema della realizzabilità, Kirousis e Papadimitriou (1988) hanno dimostrato che le immagini di scene Legoland, cioè scene con spigoli orientati solo secondo tre direzioni ortogonali (fig. 5), possono essere etichettate con complessità polinomiale. La ragione di questo è che la conoscenza della direzione degli spigoli restringe sensibilmente il numero di etichettature legali di ogni giunzione. Come conseguenza, troviamo che, adottando l'approccio linguistico descritto in precedenza, nel caso di Legoland è possibile assegnare al line drawing una proposizione booleana di una classe molto ristretta, che si risolve con algoritmi di complessità polinomiale: si tratta della classe delle proposizioni esprimibili come prodotto di somme logiche con, al più, due addendi per ogni fattore come per esempio x1 ∙ (x̅1 +x2) ∙ (x1 + x3).
Anche l'analisi di realizzabilità di un line drawing etichettato risulta notevolmente snellita nel caso di Legoland. Il ricorso alla programmazione lineare non è più necessario e il problema della ricostruzione quantitativa si può ridurre a una semplice applicazione della teoria dei grafi. Il risultato finale è una ricostruzione della struttura della scena che è unica a meno di un numero di fattori di scala pari al numero di componenti fisicamente connesse raffigurate nelline drawing (tale numero si può facilmente determinare a partire dall' etichettatura).
Il vincolo che una scena appartenga a Legoland è certamente un vincolo molto forte, eppure Legoland cattura le caratteristiche essenziali di molte scene d'interni, nelle quali gli oggetti più importanti sono spesso costituiti da parti rettangolari con spigoli che seguono l'orientazione delle pareti (rettangolari anch'esse). Ma l'importanza del caso Legoland sta - oltre che nel costituire un esempio non banale di una classe di scene per le quali l'interpretazione di un line drawing è possibile nel caso peggiore con complessità polinomiale - nel fatto che sono disponibili diverse tecniche per l' estrazione dei punti di fuga da un'immagine reale, e che queste tecniche funzionano particolarmente bene nel caso di Legoland, permettendo di determinare le tre direzioni principali della scena senza doverle fornire a priori. Per questa e altre ragioni, legate alla loro semplicità strutturale, l'estrazione di un line drawing da un' immagine di scene Legoland sembra un compito meno improbo di quello analogo per scene generiche, come verrà spiegato più in dettaglio nella seconda parte di questo saggio.
I risultati riguardanti l' etichettabilità e la realizzabilità di un line drawing di una scena Legoland sono stati poi estesi a un numero arbitrario di direzioni (Parodi e Torre, 1994; Parodi e Piccioli, 1996); data la conoscenza dei punti di fuga nell'immagine, anche in questo caso la complessità del problema dell'etichettabilità diventa polinomiale. Nel caso che il numero di punti di fuga sia uguale a tre ci si riconduce al caso di Legoland.
L'estrazione di un line drawing
Nella prima parte di questo saggio abbiamo delineato alcuni metodi per la ricostruzione della struttura tridimensionale di una scena da una singola immagine. Per far questo abbiamo dato per assunto che fosse già disponibile una rappresentazione schematica dell'immagine, un cosiddetto line drawing. Abbiamo, in altri termini, risolto il problema concentrando ci sul ragionamento logico e geometrico che conduce alla ricostruzione della scena e abbiamo ignorato il processo che consente di ottenere un line drawing a partire da un'immagine grezza. Per immagine grezza si intende, nel nostro caso, una matrice di 512 x 512 elementi, o pixel, a ognuno dei quali è associato un valore di intensità luminosa, o livello di grigio, che va da 0 (nero) a 255 (bianco). Questo è il problema più spinoso dell'intero processo interpretativo, a cui dedicheremo la seconda parte della trattazione. Le soluzioni presentate potranno sembrare, anche a ragione, incomplete e non del tutto soddisfacenti. Occorre sottolineare che l'interpretazione automatica di un'immagine a livelli di grigio è un problema che la visione artificiale non è ancora riuscita a risolvere in modo generale e convincente anche nel caso di scene poliedriche. Gli esempi mostrati di seguito non intendono perciò convincere chi legge della efficacia e affidabilità di tali tecniche in circostanze generali ma, semplicemente, mostrare in quali condizioni queste tecniche sono d'aiuto, quali sono i loro limiti e come occorre modificare i metodi di interpretazione discussi precedentemente per adattarsi ai line drawing estratti da immagini reali.
I metodi per l'estrazione di un line drawing si possono schematicamente dividere in due categorie, quella delle tecniche non contestuali, o bottom-up, in cui l'immagine viene interpretata facendo scarso uso di conoscenze a priori della scena fotografata, e quella delle tecniche contestuali, o topdown, in cui le conoscenze a priori giocano un ruolo essenziale. Naturalmente questa classificazione non è sempre soddisfacente e gli stessi metodi di estrazione che useremo a illustrazione delle due categorie sono in realtà ibridi.
Line drawing estratti con tecniche non contestuali
Un possibile approccio al problema della comprensione di un'immagine è quello di partire dall'immagine grezza ed estrarne informazione con livelli di astrazione crescente. Si può cominciare, per esempio, da semplici elaborazioni dell'immagine, quali l'individuazione delle variazioni d'intensità luminosa (livello di grigio) e di altre proprietà locali, così da ottenere quello che D. Marr (1982) ha chiamato 'schizzo primario' passando attraverso l'individuazione delle superfici e di alcune loro proprietà geometriche quali l'orientazione e la distanza dall'osservatore (il cosiddetto schizzo di dimensione 2 e 1/2, introdotto sempre da Marr) per finire con una descrizione degli oggetti, della loro posizione e orientazione nella scena e delle relazioni spaziali e fisiche tra loro. In questo approccio gioca parte essenziale l'assunto che per ottenere l'informazione a un dato livello di astrazione si utilizza solo l'informazione presente nei livelli di astrazione inferiori.
Abbandoniamo ora queste considerazioni di carattere generale e delineiamo una possibile strategia bottom-up in cinque stadi per estrarre un line drawing da un'immagine grezza.
Estrazione dei contorni. - Il primo stadio è l'individuazione dei cosiddetti contorni, cioè delle brusche variazioni di luminosità (livelli di grigio) dell'immagine. L'idea sottostante è che tali contorni corrispondano alle discontinuità di profondità o di orientazione delle superfici componenti la scena. Nel caso di una scena composta esclusivamente da poliedri con superfici prive di tessitura (cioè uniformi, prive di disegno), illuminate da un'unica sorgente di luce, tali discontinuità corrispondono agli spigoli della scena e a eventuali ombre. Una volta estratti i contorni, questi vengono perciò provvisoriamente identificati con gli spigoli della scena dopo alcune ulteriori elaborazioni. Tale identificazione è quasi sempre problematica, soprattutto per immagini di scene che non si arrendono alla semplice schematizzazione di poliedri con superfici uniformi; nonostante questo, un osservatore è quasi sempre in grado di distinguere gli oggetti presenti nell' immagine a partire dall' immagine dei contorni estratti con uno degli algoritmi disponibili.
In passato sono stati proposti numerosi metodi per l'estrazione dei contorni; uno tra i più efficienti è quello che identifica i contorni con i massimi del gradiente di intensità nella direzione del gradiente (Canny, 1986). Alcuni esperimenti hanno confermato che il metodo offre diversi vantaggi rispetto al classico approccio di Marr (1982) in cui i contorni vengono identificati con gli zeri dell' operatore laplaciano dell' intensità luminosa. Osserviamo che da un punto di vista generale l'estrazione dei contorni può essere considerato un problema di differenziazione: per individuare le brusche variazioni di luminosità occorre applicare all'immagine operatori differenziali quali il gradiente o illaplaciano. L'estrazione dei contorni soffre, quindi, come tutti i problemi di differenziazione, di instabilità numerica. Errori anche piccoli nell' immagine vengono amplificati dalla differenziazione generando errori di notevole entità sui contorni estratti. In altri termini, l'estrazione dei contorni è un problema mal posto nel senso di Hadamard (Bertero et al., 1988). A questa instabilità numerica si può in parte rimediare estraendo i contorni non dall' immagine originale ma dall' immagine dopo che è stata filtrata da un operatore che taglia le alte frequenze, che, cioè, tenta di eliminare le variazioni rapide di luminosità dovute alla presenza di rumore (filtro passa-basso). L'estrazione dei contorni si può, perciò, eseguire innanzitutto effettuando la convoluzione dell' immagine I(x, y) con un filtro gaussiano
,
dove σ è un parametro opportuno. Si ottiene così l'immagine filtrata IF(x,y) = I (x,y) * G(x,y) (ricordiamo che l'operatore di convoluzione unidimensionale tra due funzioni f, g, indicato dal simbolo *, si definisce come
l'estensione al caso bidimensionale è banale). Successivamente si calcola il gradiente dell'immagine filtrata IF(x, y):
∇IF(x,y) = I(x,y) * ∇G(x,y)
(come si vede, l'operatore ∇ può essere applicato - sfruttando elementari proprietà dell'operatore ∇ e della convoluzione - direttamente sul filtro gaussiano G(x,y), con notevole alleggerimento computazionale).
A questo punto i contorni vengono identificati con i punti di massimo di ∣ ∇IF(x,y) ∣² lungo la direzione di ∇IF(x,y), e i contorni per i quali il modulo del gradi ente è inferiore a una certa soglia vengono eliminati.
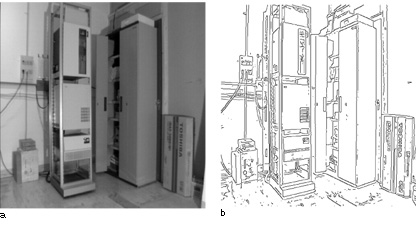
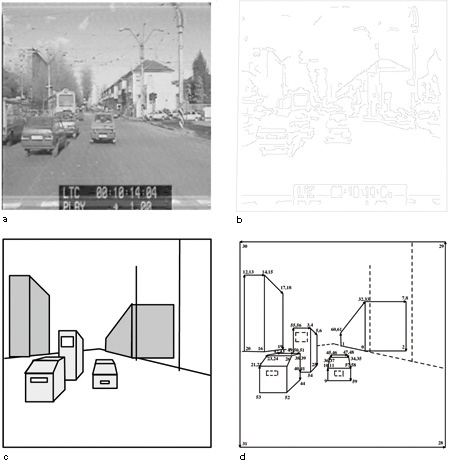
La figura (fig. 6) mostra un esempio di estrazione dei contorni per una scena di interni.
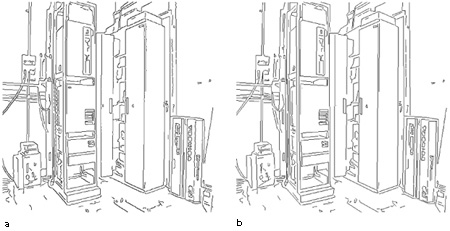
Inseguimento dei contorni. - Come risultato della fase di estrazione dei contorni, ogni elemento dell'immagine (pixel) è stato classificato come punto di contorno o come punto interno. I punti di contorno così trovati devono ora essere raccolti in 'catene' di punti che si suppone siano immagine dello stesso spigolo fisico, sia per rappresentare l'informazione ottenuta in modo più strutturato che per trattare meglio i problemi legati al rumore, all'illuminazione complessa e ad altre fonti di disturbo che provocano la presenza di punti di contorno spuri, spezzamento di 'catene' di punti di contorno appartenenti allo stesso spigolo, e così via. Tra le varie tecniche che si possono usare per costruire le 'catene', citiamo quella che consiste nell'analizzare le caratteristiche dei pixel in un piccolo intorno (per esempio, 3 x 3 o 5 x 5) di ogni punto di contorno, e nel legare tra loro punti che hanno valori simili del modulo del gradi ente di luminosità nella sua direzione (Gonzales e Wintz, 1987). In figura (fig. 7) è rappresentato un esempio dell'inseguimento dei contorni.
Approssimazione poligonale. - Siccome abbiamo dato per assunto che gli oggetti di interesse nella scena siano poliedrici, è utile elaborare ulteriormente l'informazione ottenuta fino a questo momento per renderla più compatta e più vicina alla forma finale, approssimando le catene di segmenti estratte nella fase di inseguimento dei contorni con segmenti di retta (o, più in generale, con spezzate). Per fare questo è possibile utilizzare una delle tante tecniche di approssimazione poligonale (v. figura 7). Tra le più semplici, citiamo quella di U.E. Ramer (O'Gorman e Kasturi, 1995) nella quale si comincia connettendo i due punti estremi di una catena con un segmento di retta; si calcola quindi la distanza di ogni punto della catena dal segmento così disegnato, e se la distanza massima è maggiore di una certa soglia, si spezza il segmento in due segmenti che vanno dagli estremi della catena al punto della catena con la massima distanza dal segmento di retta iniziale; si ripete quindi la procedura in modo iterativo fino a quando tutti i punti della catena sono a una distanza dalla spezzata inferiore a una certa soglia. Questo semplice metodo non è del tutto soddisfacente per i nostri scopi, in quanto, benché approssimi con precisione arbitraria ogni catena di punti di contorno, non è affatto preciso nel determinare la pendenza di ogni segmento di retta componente la spezzata, o i punti critici della catena, dove la pendenza cambia bruscamente. Conviene perciò usare metodi un po' più sofisticati, che consentono di stimare con calcoli di curvatura i punti critici della catena (O'Gorman e Kasturi, 1995) e, quindi, approssimare ogni tratto a curvatura costante (nulla nel caso di catena lineare) con un segmento di retta.
Segmentazione. - Da un punto di vista generale, le tre fasi discusse precedentemente altro non sono che passi intermedi per ottenere la cosiddetta segmentazione del! 'immagine, cioè una suddivisione dell'immagine in regioni con proprietà omogenee. Cosa si intenda per 'proprietà omogenee' dipende naturalmente dagli scopi per i quali si esegue la segmentazione: si può trattare di una regione con luminosità uniforme, o con caratteristiche uniformi di tessitura (in questo caso, esiste una scala appropriata alla quale osservare la tessitura), oppure di una regione corrispondente a un certo oggetto 3D, eventualmente complesso. La figura (fig. 8) mostra un esempio di segmentazione di un'immagine da satellite in regioni a tessitura omogenea.
Nel nostro caso, siccome lo scopo è di ottenere un line drawing della scena, le regioni elementari che interessano sono le proiezioni delle facce piane dei poliedri componenti la scena. In generale, la segmentazione di un'immagine in un certo numero di regioni distinte significative è un problema di notevole difficoltà, sul quale si è molto lavorato fin dalla nascita della visione artificiale, ma riguardo al quale valgono ancora, almeno in parte, le parole di Marr che, alla fine degli anni Settanta, notava come "a dispetto di considerevoli sforzi protratti per lungo tempo, la teoria e la pratica della segmentazione sono rimaste a un livello primitivo" e questo perché "è praticamente impossibile formulare precisamente quali [siano] esattamente gli obiettivi della segmentazione in termini dell'immagine o anche del mondo fisico". Inoltre, quand'anche questi problemi di formulazione fossero risolti per una particolare situazione, la soluzione non sarebbe direttamente utilizzabile per risolverne un'altra. In realtà, da allora, sono stati ottenuti diversi risultati teorici e pratici di notevole interesse sulla segmentazione, utilizzando tecniche a basso livello che incorporano strumenti mutuati dalla statistica, dalla teoria dell'informazione, dalla teoria della complessità descrittiva di Kolmogorov e così via, senza riferimento esplicito al ragionamento geometrico ad alto livello. Tra le acquisizioni teoriche, va menzionato il risultato di D. Mumford e J. Shah sull'esistenza di una segmentazione che minimizza un appropriato funzionale di forma molto generale, tale che i contorni delle regioni in cui l'immagine viene segmentata siano curve continue a tratti (e non, per esempio, frattali). L'interesse di questo risultato, discusso approfonditamente da J.M. Morel e S. Solimini (1995), sta nel fatto che una classe molto vasta di tecniche di segmentazione può essere riformulata come un metodo per minimizzare tale funzionale. Va inoltre detto che la stessa estrazione dei contorni è un problema di segmentazione sia nella sostanza che nella forma, e che gli argomenti per rifiutare un approccio in chiave di segmentazione a certi problemi di visione si possono facilmente trasformare in argomenti contro l'uso della stessa estrazione dei contorni (Morel e Solimini, 1995). Al di là di queste importanti acquisizioni teoriche e pratiche, però, il problema di una segmentazione 'intelligente' resta aperto, e presenta la stessa difficoltà di quello generale dell'interpretazione di un'immagine.
Vediamo ora che cosa significa segmentazione, in concreto, nel nostro contesto: l'obiettivo è associare a ogni superficie piana una e una sola regione del piano immagine (un poligono). Per far questo, si può utilizzare a titolo esemplificativo un algoritmo che esegue alcune operazioni sui segmenti ottenuti nella fase di approssimazione poligonale che comprende la fusione di segmenti adiacenti e collineari, l'individuazione dei vertici e la rimozione di quelli con un solo segmento incidente. Osserviamo che queste operazioni si eseguono in maniera molto più affidabile se è disponibile qualche informazione supplementare sulla scena. Per esempio, in alcuni degli esperimenti che mostreremo i line drawing sono stati ottenuti nell'ipotesi che la scena fosse Legoland. Questa ipotesi viene sfruttata già a partire da questa fase, in cui avviene la fusione dei segmenti e la costruzione dei poligoni; la sua utilità consiste nel fatto che rende possibile la determinazione dei punti di fuga, la classificazione di segmenti come appartenenti a uno dei tre punti di fuga o come estranei e, infine, l'eliminazione dei segmenti estranei e la ricostruzione dei poligoni in modo 'più pulito'.
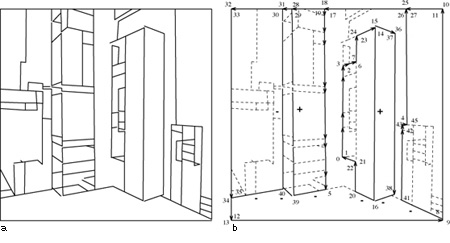
Alla fine di queste operazioni si ha un insieme di regioni bidimensionali (2D) che rappresenta solitamente una sovrasegmentazione dell'immagine: molte regioni diverse corrispondono alla stessa superficie piana (fig. 9). A questo punto è possibile fondere tra loro poligoni con criteri euristici (Straforini et al., 1992), o affidare alla fase di etichettatura il compito di scremare l'insieme dei segmenti. Negli esperimenti riportati è stato seguito quest'ultimo approccio. In ogni caso nelline drawing alla fine dello stadio di segmentazione sono presenti, in generale, difetti come segmenti mancanti, segmenti spuri, giunzioni mal localizzate e giunzioni di tipo più complesso di quelle presenti nel catalogo di Huffman e Clowes. Per questa ragione, le procedure di etichettatura e di ricostruzione quantitativa, delineate nella prima parte di questo saggio, non possono essere utilizzate senza modifiche.
Interpretazione 3D. – Sia che si usi la conoscenza a priori sulla scena (per esempio, l’ipotesi che la scena sia Legoland), sia che si usino strumenti più generali e per questo meno efficienti nei singoli casi, alla fine dell'elaborazione ci si trova di fronte a un line drawing imperfetto. Spesso il line drawing è così imperfetto che il ricorso all'etichettatura è inutile e tutto quello che si può fare è un'analisi dei contenuti più grossolani della scena. Quello che impedisce una ricostruzione più precisa è la mancata individuazione di molti segmenti. Nonostante molti autori abbiano proposto fin dall'inizio metodi per ritrovare segmenti perduti, nessun metodo riesce a far fronte a immagini di tale complessità. Nei casi in cui siano stati trovati tutti i segmenti necessari a una ricostruzione quasi corretta dell'immagine (una strategia può essere quella di abbassare le soglie dell'estrazione di contorni, in modo da aumentare il rumore ma perdere meno segmenti), si può in linea di principio risolvere il problema dell'etichettatura introducendo una nuova etichetta. Accanto ai segmenti di connessione (etichette + e -) e ai segmenti occlusivi (etichette → e ←), vengono introdotti segmenti indicati con un tratteggio, che possono corrispondere a fenditure, ombre, disegni su un pannello, o semplicemente segmenti spuri. Utilizzando le regole usuali di Huffman e Clowes e alcune regole euristiche addizionali, è possibile etichettare il disegno in modo che almeno una delle etichettature possibili sia quella che corrisponde all'interpretazione più naturale. Una tale etichettatura può essere generata con i metodi discussi in precedenza. Occorre però osservare che in generale questi metodi hanno complessità esponenziale, a differenza degli algoritmi di etichettatura per le scene Legoland che si possono applicare quando non ci sono segmenti spuri. Inoltre, il numero di etichettature possibili cresce a sua volta esponenzialmente con il numero di segmenti delline drawing; ciò è vero anche per il caso Legoland, ma le costanti coinvolte in questo andamento esponenziale sono drasticamente diverse. Questa è una delle ragioni per cui un approccio bottom-up non è praticabile.
Ottenuta tale etichettatura, la ricostruzione può essere portata a termine utilizzando la procedura di Sugihara esposta precedentemente o, quando questo sia possibile, sfruttando i procedimenti semplificati disponibili per le scene Legoland, ignorando in una prima fase i segmenti tratteggiati. È banale, tuttavia, trovare la posizione 3D di possibili fenditure, ombre o disegni corrispondenti a questi segmenti, dopo che la ricostruzione 3D è stata compiuta e ogni pannello piano è stato localizzato nello spazio 3D. Per esempio, la figura 6a riporta una scena Legoland piuttosto complicata. Dopo le elaborazioni relative all'estrazione dei contorni (v. figura 6b), all'inseguimento dei contorni (v. figura 7a) e all'approssimazione poligonale (v. figura 7b) vengono estratti i punti di fuga (Straforini et al., 1992), e si procede quindi alla segmentazione. Il line drawing di figura 9a ha molti segmenti mancanti e molti segmenti spuri; tuttavia, l'etichettatura mostrata nella figura 9b permette di ricostruire le caratteristiche più importanti della scena 3D. Nel line drawing etichettato vi è una sola componente fisica; di conseguenza è sufficiente determinare un singolo fattore di scala per avere una ricostruzione 3D completa. Nel nostro caso, il fattore di scala è determinato dalla conoscenza della larghezza del server in primo piano (0,56 ± 0,01 m), che consente di assegnare una posizione 3D a tutti i vertici raffigurati nel line drawing. Come controprova, si può calcolare con l'algoritmo l'altezza dell' armadio sulla destra (1,75 ±0,30 m), e confrontarla con la sua altezza misurata (1,95 ± 0,02 m). Si noti l'ampio errore con cui viene determinata la posizione dei vertici. La figura (fig. 10) è la fotografia di un insieme di scatole appoggiate su un tavolo. Poiché non si tratta di una scena Legoland, l'estrazione delline drawing non può trarre vantaggio dall'estrazione automatica dei punti di fuga. Il line drawing che si ottiene è piuttosto fedele, in quanto non vi sono segmenti mancanti e sono presenti solo due segmenti spuri, vicini ai due vertici visibili del tavolo. È possibile eseguire l'etichettatura (v. figura 10b) come nel caso precedente, ma per quanto riguarda la ricostruzione quantitativa, anche in questo caso vi è una sola componente fisicamente connessa. Tuttavia, senza la conoscenza dei punti di fuga non è possibile fare una ricostruzione quantitativa unica a meno di un fattore di scala, ma solo determinare la realizzabilità con la procedura di Sugihara. Se, invece, vengono forniti punti di fuga dall' operatore, la ricostruzione con tecniche simili a quelle usate per Legoland è fattibile anche se la scena non è Legoland (Parodi e Piccioli, 1996).
Line drawing estratti con tecniche contestuali
Per la quasi totalità delle immagini di scene di esterni e di interni, non è possibile estrarre un line drawing anche solo grossolanamente corretto in modo automatico con una serie di elaborazioni bottom-up. Un approccio più promettente, sul quale si stanno muovendo i primi passi, è quello che chiameremo contestuale. L'idea chiave è che ricostruire la scena raffigurata in un'immagine è tanto più semplice quanto maggiore è l'informazione che possediamo a priori sul contenuto della scena. Non si tratta di un'idea recente; fin dai primi lavori di visione artificiale molti autori hanno sottolineato l'importanza della conoscenza a priori nel risolvere i problemi di visione più svariati, e molti di questi soprattutto legati al riconoscimento di oggetti noti in un'immagine - sono stati risolti con successo in questa cornice contestuale (Strat e Fischler, 1991). Per quanto riguarda il problema dell'estrazione di un line drawing da una scena reale, però, esistono solo alcuni studi preliminari sull'argomento (Parodi e Piccioli, 1996).
Apriamo una breve parentesi sul problema del cosiddetto riconoscimento di oggetti, cioè la ricerca nell'immagine di un particolare oggetto 3D dalle caratteristiche note. Si tratta di un problema complesso, anche se più semplice della ricostruzione di un ambiente con oggetti di forma scono sci uta, e per il quale sono disponibili numerose tecniche (Jain e Flynn,1993). Le più semplici tra queste si basano su varianti del semplice confronto diretto tra modello e immagine (template-matching): dato un certo numero di modelli di oggetti possibili, essi vengono ruotati e traslati nel tentativo di farli coincidere con una parte determinata dell'immagine. Tra i metodi più sofisticati consideriamo quelli che ricorrono al calcolo di quantità invarianti (che, cioè, rimangono le stesse per un certo gruppo di trasformazioni, tipicamente, traslazioni e rotazioni, sull'oggetto) effettuando un cosiddetto indexing, che consiste nell'associare a ogni oggetto un certo numero di quantità invarianti. La coincidenza di tali quantità invarianti è condizione necessaria affinché l'oggetto venga identificato con un certo modello. Altri metodi si fondano sull'individuazione di una 'firma' (approcci signature-based), cioè cercano qualche caratteristica distintiva dell'oggetto e solo in un secondo tempo verificano quantitativamente che l'oggetto corrisponda a quello cercato. L'approccio signature-based è, tra i vari approcci al riconoscimento, uno dei pochi che si possa estendere al caso di oggetti non determinati rigidamente ma definiti a meno di un certo numero di parametri o in modo ancora più generale. Perciò, questo approccio si adatta a situazioni nelle quali non si tratta di riscontrare la presenza nell'immagine di un oggetto particolare ma di un elemento di un'intera classe di oggetti come, per esempio, la 'classe palazzo' o la 'classe albero' in un'immagine di una scena stradale.
Mostreremo un esempio in cui l'approccio contestuale viene usato per la ricostruzione di una scena stradale. L'idea è quella di operare la ricostruzione 3D di una scena sconosciuta utilizzando procedure di riconoscimento basate sulla 'firma' di vari oggetti presenti nella scena. La conoscenza a priori riguarda tre diversi aspetti del problema. lnnanzitutto, la struttura generale della scena, che si dà per assunto essere di tipo Legoland, almeno per quanto riguarda gli elementi fondamentali come il manto stradale, i palazzi e così via. Il secondo aspetto riguarda il processo di acquisizione, in cui si dà per assunto che la telecamera sia parallela al manto stradale e che miri in avanti; come conseguenza, ci sono due punti di fuga all'infrnito e un punto di fuga al centro dell'immagine. Infine, si considerano gli oggetti e viene avanzata l'ipotesi che ogni oggetto che compare nella scena appartenga a una certa classe come, per esempio, 'albero', 'casa', 'automobile' e così via).
Il line drawing viene quindi ricavato in fasi successive. Dapprima si estrae la struttura generale, grossolana della scena 3D, sfruttando l'informazione a priori sull'ambiente e sul processo di acquisizione; tale informazione viene usata per raggruppare i segmenti in quattro categorie a seconda che convergano a uno dei tre punti di fuga o siano segmenti di altro tipo, e per eseguire una segmentazione preliminare dell'immagine nelle quattro regioni corrispondenti all'incirca al manto stradale, al cielo e alle due regioni laterali dove possono trovarsi edifici e altri oggetti. Successivamente si seleziona un opportuno insieme di caratteristiche per ogni classe di oggetti che possono essere presenti nella scena: per esempio, per un albero è possibile aspettarsi - almeno in primavera e in estate - che siano presenti una regione verde e una marrone, che i segmenti ricavati con l'estrazione dei contorni corrispondenti alla regione verde siano molto 'disordinati' e che le regioni verdi e marrone stiano in una delle due regioni laterali, e così via. In seguito gli oggetti vengono identificati e classificati in base alle caratteristiche suddette; a identificazione avvenuta, si estraggono eventualmente altre caratteristiche significative non comprese nella 'firma' come, per esempio, alcune peculiarità della forma. Infine viene creato un line drawing composto di una versione schematica dei vari oggetti individuati nella scena.
Un esempio di applicazione di questo metodo si può vedere in figura (fig. 11), che mostra un'immagine di una tipica scena stradale e alcune elaborazioni. L'immagine è stata estratta da una sequenza acquisita per mezzo di una telecamera posta su un veicolo mobile, a un'altezza di 1,70 m dal suolo, spostata di 0,21 m a destra rispetto all'asse del veicolo. Il line drawing finale, già etichettato, è riportato nella figura 11d dove è possibile osservare che, per problemi di scala, sia i segmenti di tipo + che quelli di tipo - sono stati disegnati come segmenti semplici. I punti di fuga sono stati estratti automaticamente dall'immagine (Straforini et al., 1992). All'etichettatura mostrata corrispondono i 61 vertici contrassegnati nella stessa figura dal loro numero di identificazione.
Il line drawing etichettato ha una sola componente fisicamente connessa, in quanto tutti gli oggetti sono connessi tra loro dal fondo stradale. Il fattore di scala (che quindi è unico) è stato fissato imponendo che la larghezza dell' auto nella parte sinistra dell'immagine sia 150 ± 5 cm. Questa informazione può essere, quindi, usata per ottenere, con un procedimento di ricostruzione quantitativa cui si è accennato in precedenza, una stima delle dimensioni degli oggetti presenti nella scena (tab. I).
Osserviamo che in un approccio del tipo sopra descritto è difficile, in realtà, distinguere nettamente la fase in cui il line drawing viene estratto da quella in cui viene interpretato. Se i dettagli sulla posizione e la dimensione esatta in 3D degli oggetti possono essere ricostruiti solo sulla base del line drawing, parte dell'informazione va inserita, anche solo provvisoriamente, già durante l'estrazione stessa delline drawing. Per giustificare questa procedura, si pensi solo ai problemi di occlusione tra i diversi oggetti. La dimensione di tutti gli oggetti che compaiono nella scena può essere così determinata e confrontata con la loro dimensione reale.
La conclusione di questa parte del saggio dedicata all'estrazione di un line drawing da un'immagine grezza, è che l'approccio bottom-up pone, nel migliore dei casi, gravi problemi di complessità. Tale approccio, in generale, fornisce risultati miseri anche dove si richieda solo una ricostruzione grossolana e dove si sfruttino conoscenze a priori di tipo generale (per esempio, l'ipotesi di mondo Legoland) ponendosi così parzialmente fuori dallo schema bottom-up.
L'approccio contestuale, invece, appare molto più promettente ed efficace di quello non contestuale. In futuro, tuttavia, dovranno essere risolti numerosi problemi prima che lo si possa applicare in modo affidabile a una vasta classe di casi di ricostruzione. Tutt'oggi, la conoscenza a priori sulla scena deve essere molto ampia, e la classe di scene che si possono affrontare con questo metodo è alquanto ristretta. L'analisi di scene stradali semplici è un esempio interessante perché si tratta di un mondo semplificato in cui si può dire molto sulla struttura generale della scena e il tipo di oggetti presenti, ma, allo stesso tempo, si tratta di un ambiente a priori sconosciuto e non rigidamente determinato. Un problema specifico dell'approccio contestuale signature-based che abbiamo descritto è che la sua applicabilità pratica dipende drasticamente dalla presenza di un numero limitato di classi di oggetti tra loro ben distinguibili in base alla 'firma'. All'aumentare del numero delle diverse classi, è sempre più difficile trovare 'firme' distintive per ognuna di esse.
Conclusioni
La visione artificiale è una disciplina ancora in espansione e, per diversi aspetti, non ancora matura. Molti problemi che hanno motivato la ricerca fin dai primi anni Sessanta come quelli di visione high level, quali il riconoscimento di oggetti e la ricostruzione della struttura tridimensionale di una scena, non sono ancora stati risolti in modo soddisfacente. Sono in discussione le metodologie stesse necessarie per affrontare questi problemi. Tuttavia, sono stati ottenuti diversi risultati teorici e pratici di notevole interesse; alcuni riguardano proprio l'interpretazione di un'immagine tramite l'estrazione di un line drawing, problema attorno al quale abbiamo incentrato la nostra discussione. Anche se una soluzione completa di questo problema, pur se in ambiti ristretti, continua a eludere gli sforzi dei ricercatori, si tratta, comunque, di un ambito della visione high level per il quale esiste una teoria ben articolata, con risultati teorici di notevole dignità formale e con risultati pratici di grande interesse.
Bibliografia citata
BERTERO, M., POGGIO, T., TORRE, V. (1988) Ill-posed problems in early vision. Proceedings of the IEEE, 76 (8), 869-889.
BIZAIS, Y., BARILLOT, C., DI PAOLA, R. (1995) Inlormation processing in medicaI imaging, Dordrecht, Kluwer.
BLAKE, A., ZISSERMAN, A. (1987) Visual reconstruction. Cambridge, Mass., MIT Press.
CANNY, J. (1986) A computational approach to edge detection. IEEE Transactions on Pattern Analysis and Machine Intelligence, 8(6), 679-698.
DICKMANNS, E.D., MYSLIWETZ, B.D., CHRISTIANS, T. (1990) An integrated spatio-temporal approach to automatic visual guidance of autonomous vehicles. IEEE Transactions on Systems, Man and Cybernetics, 20 (5), 1273-1284.
ERNST, B. (1986) Escher's impossible figures in a new context. In M. C. Escher: art and science, proceedings 01 the International Congress on M. C. Escher, Rome, Italy, 26-28 March 1985, a c. di Coxeter H.S.M. et al., Amsterdam-New York, Elsevier Science Publishers.
FAUGERAS, O.D. (1993) Three-dimensional computer vision, Cambridge, Mass., MIT Press.
GAREY, M.R., JOHNSON, D.S. (1979) Computers and intractability: a guide to the theory of NP-completeness, San Francisco, W.H. Freeman.
GEMAN, D., GEMAN, S., GRAFFIGNE, C., DONG, P. (1990) Boundary detection by constrained optimization. IEEE Transactions on Pattern Analysis and Machine Intelligence, 12 (7), 609-628.
GONZALEZ, R.C., WINTZ, P. (1987) Digital image processing Reading, Mass., Addison-Wesley.
JAIN, A.K., FLYNN, P.J. (1993) Three dimensional object recognition systems. Amsterdam-New York, Elsevier Science Publishers.
KIROUSIS, L.M., PAPADIMITRIOU, C.H. (1988) The complexity of recognizing polyhedral scenes. Journal of Computer and System Sciences, 37, 14-38.
LI, S.Z. (1995) Markov randomfield modeling in computer vision, New York, Springer Verlag.
MACKWORTH, A.K., FREUDER, E.C. (1993) The complexity of constraint satisfaction revisited. Artificial Intelligence, 59, 57-92.
MARR, D. (1982) Vision: a computational investigation into the human representation and processing of visual information, San Francisco, W.H. Freeman.
MOREL, J.-M., SOLIMINI, S. (1995) Variational methods in image segmentation: with seven image processing experiments, Birkhäuser, Boston.
MUNDY, J.L., ZISSERMAN, A. (1992) Geometric invariance in computer vision, Cambridge, Mass., MIT Press.
O'GORMAN, L., KASTURI, R. (1995) Document image analysis. Los Alamitos, IEEE Computer Society.
PARODI, P., LANCEWICKI, R., VIJH, A., TSOTSOS, J.K. (1996) Empirically-derived estimates of the complexity of labelling line drawings. Technical Report RBCV-TR-96-52, Dept. of Computer Science, University of Toronto.
PARODI, P., PICCIOLI, G. (1996) 3D shape reconstruction by using vanishing points. IEEE Transactions on Pattern Analysis and Machine Intelligence, 18 (2), 211-217.
PARODI, P., TORRE, V. (1994) On the complexity of labeling line drawings of polyhedral scenes. Artificial Intelligence, 70, 239-276.
PA VLIDIS, T. (1982) Algorithms for graphics and image processing. Rockville, MD, Computer Science Press.
STRAFORINI, M., COELHO, C., CAMPANI, M., TORRE, V. (1992) The recovery and understanding of a line drawing from indoor scenes. IEEE Transactions on Pattern Analysis and Machine Intelligence, 14 (2), 298-303.
STRAT, T.M., FISCHLER, M.A. (1991) Context-based vision: recognizing objects using information from both 2D and 3D imagery. IEEE Transactions on Pattern Analysis and Machine Intelligence, 13 (10), 1050-1065.
SUGIHARA, K. (1986) Machine interpretation of fine drawings, Cambridge, Mass., MIT Press.
TSOTSOS, J.K. (1990) A complexity level analysis ofvision. Behav. Brain Sci., 13 (3), 423-455.
VERRI, A., STRAFORINI, M., TORRE, V. (1992) Computational aspects of motion perception in natural and artificial vision systems. Philos. Trans. R. Soc. Lond. Biol. Sci., 337, 429-443.
WALTZ, D. (1975) Understanding line-drawings of scenes with shadows. In The psychology of computer vision, a c. di Winston P.H., New York, McGraw-Hill, pp. 19-91.