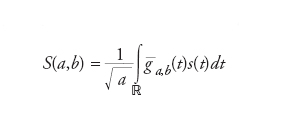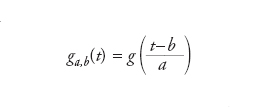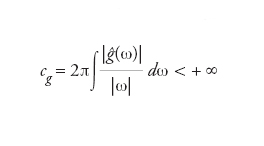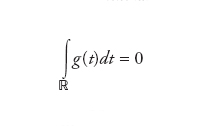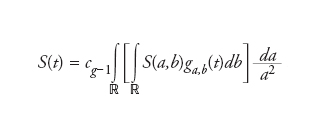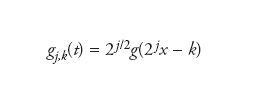wavelet

wavelet

Una funzione del tempo f(t):ℝ→ℂ sufficientemente ben localizzata tanto nella variabile temporale che in frequenza. Questa richiesta si traduce in alcune proprietà di integrabilità e soprattutto nella richiesta che i momenti ∫t^kf(t)dt si annullino per k=1,...,n con n sufficientemente grande. Esempi ben noti di wavelet (ondine) sono il cappello messicano g¹(t)=(1−t²)e^−t2/2 il wavelet di Morlet g²(t)=π^−1/4(e^−iζ0t−e^−iζ02)e^−t2. Notiamo che i grafici di g¹ e di |g²| appaiono ben concentrati intorno all’origine degli assi. Nell’analisi wavelet copie traslate e scalate di un wavelet madre g(t) sono utilizzate per studiare segnali o immagini. La trasformata wavelet continua di una funzione s(t) è la funzione di due variabili reali a>0,b definita dalla

dove

è la wavelet madre prima traslata di una lunghezza b e poi scalata di un fattore a e ḡ indica il complesso coniugato di g. Sul wavelet madre è imposta la condizione di compatibilità

dove ĝ (w) indica la trasformata di Fourier di g (t). Nel caso in cui ĝ (w) sia differenziabile, essa implica ĝ (0)=0 ossia

Assumendo la validità della condizione di compatibilità, esiste una formula di inversione

A partire da un wavelet madre g (t) è talvolta possibile definire una base dello spazio L2(ℝ,ℂ) delle funzioni a quadrato sommabile sulla retta reale e a valori complessi della forma

con j,k interi relativi. Un esempio di una tale base composto da elementi non differenziabili è la base di Haar. È interessante notare che, in generale, per ottenere una base wavelet costituita da funzioni regolari (differenziabili più volte) si è costretti ad allargare gli intervalli in cui queste ultime sono diverse da zero (supporti). L’analisi wavelet si è dimostrata particolarmente adatta per l’analisi e l’individuazione di proprietà di segnali, funzioni o immagini quali discontinuità o la presenza di strutture frattali: le wavelet sono state definite un microscopio matematico.

→ Perceptron