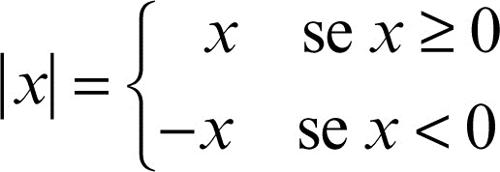Z

Z

Z (insieme dei numeri interi) insieme numerico che estende l’insieme N dei numeri naturali. È l’unione dell’insieme dei numeri interi positivi

dell’insieme dei numeri interi negativi

e dell’insieme formato dal solo zero {0}. I numeri interi sono anche detti numeri interi relativi e tra essi i positivi possono anche essere scritti senza il segno +. La lettera Z, che indica il loro insieme, è l’iniziale del termine tedesco Zahl («numero»).

I numeri negativi hanno origini remote. Inizialmente erano accettati come indicazioni di debiti, ma già in Brahmagupta (vi secolo) si accenna alla regola dei segni per la moltiplicazione dei numeri interi. Tuttavia, la loro piena dignità concettuale stenta ad affermarsi; ancora R. Bombelli, nel xvi secolo, ne parla come di numeri surdi (cioè «assurdi») e anche Cartesio, che peraltro formula la regola dei segni che porta il suo nome (→ Cartesio, regola di), chiama false le soluzioni negative di un’equazione. La motivazione algebrica dell’ampliamento da N a Z sta nel fatto che se a e b sono due numeri naturali, non sempre è definito in N il risultato della sottrazione a − b; equivalentemente, non tutte le equazioni del tipo x + b = a hanno soluzione in N: ciò avviene se e solo se a è maggiore o uguale di b. Tale situazione esprime il fatto che l’insieme N dei numeri naturali dotato dell’operazione + di addizione non è un gruppo, ma un → monoide: nessun elemento diverso da 0 ammette inverso rispetto all’addizione. L’insieme Z dei numeri interi è introdotto proprio per risolvere questo tipo di equazioni: ogni suo elemento è soluzione di una siffatta equazione e, viceversa, ogni siffatta equazione ha soluzione in Z.

Nel prodotto cartesiano N × N si introduce la relazione di → equivalenza (a, b) ∼ (c, d) se e solo se a + d = b + c, dove (a, b) e (c, d) sono due arbitrari elementi di N × N. Si definisce quindi l’insieme Z come l’→ insieme quoziente di N × N rispetto a tale relazione di equivalenza: Z = (N × N)/∼.

Un numero intero relativo è un elemento di Z e quindi coincide con una classe di equivalenza della forma [(a, b)], definita come

Tale definizione formale significa che, per esempio, le coppie (2, 0), (3, 1), (4, 2), …, definiscono tutte lo stesso numero positivo, generalmente indicato come +2 o più semplicemente 2. Analogamente, le coppie (0, 2), (1, 3), (2, 4), …, definiscono lo stesso numero negativo, generalmente indicato come −2, opposto del precedente.

In Z si definiscono le due operazioni di addizione (denotata con il simbolo + e il cui risultato è detto somma) e di moltiplicazione (denotata con i simboli × o ⋅, che tuttavia sono spesso omessi, e il cui risultato

è detto prodotto) come segue:

Tali operazioni sono in effetti ben definite, nel senso che non dipendono dal particolare rappresentante considerato nella classe di equivalenza. Inoltre esse sono entrambe associative e commutative; la moltiplicazione gode della proprietà distributiva rispetto all’addizione ed entrambe le operazioni ammettono elemento neutro: 0 = [(0, 0)] è elemento neutro rispetto all’addizione mentre 1 = [(1, 0)] è elemento neutro rispetto alla moltiplicazione. Infine ogni numero intero [(a, b)] è invertibile rispetto all’addizione, con inverso [(b, a)]; due numeri inversi l’uno dell’altro rispetto all’addizione sono detti opposti. Dotato di tali operazioni, Z acquisisce pertanto la struttura algebrica di → anello commutativo unitario e, più precisamente, quella di → dominio d’integrità: ciò esprime il fatto che non esistono coppie di numeri interi diversi da 0 il cui prodotto sia 0.

L’insieme N dei numeri naturali si immerge in Z (→ immersione) tramite l’omomorfismo iniettivo i: N → Z definito da i(n) = [(n, 0)]: tale immersione conserva tanto la struttura additiva quanto quella moltiplicativa di N e permette pertanto di identificare N con il sottoinsieme di Z costituito dai numeri interi della forma [(n, 0)]; si può perciò scrivere semplicemente n anziché [(n, 0)]. Ogni numero naturale n possiede così un inverso rispetto all’operazione di addizione; vale a dire esiste il suo opposto, che coincide con il numero intero [(0, n)], indicato semplicemente con il simbolo −n. Si può quindi definire in Z l’operazione di sottrazione tra numeri naturali, indicata anch’essa con il simbolo −, che inverte l’operazione di addizione (che non è invertibile in N): se n e m sono due numeri naturali, si definisce n − m come il numero intero [(n, m)] = n + (−m). Dunque ogni equazione del tipo x + b = a, con a e b numeri naturali, possiede soluzione in Z, che consiste nel numero intero a − b = [(a, b)]; viceversa, per costruzione, Z coincide con l’insieme di tali soluzioni. Più in generale, se [(m, n)] è un qualsiasi numero intero, si indica con il simbolo −[(m, n)] il suo opposto [(n, m)]. Si può quindi definire l’operazione di sottrazione su tutto l’insieme Z dei numeri interi ponendo x − y = x + (−y), dove x e y indicano due arbitrari numeri interi.

A partire dalla relazione d’ordine ≤ definita in N, si introduce in Z una relazione d’ordine (sempre indicata con il simbolo ≤) la quale estende quella definita in N: se x = a − b e y = c − d sono due numeri interi (dove a, b, c e d sono numeri naturali), allora si pone x ≤ y se e solo se a + d ≤ b + c.

Se x ≤ y, si dice allora che x è minore o uguale di y; equivalentemente si scrive anche y ≥ x e si dice che y è maggiore o uguale di x. Poiché l’ordinamento ≤ definito su N è totale e compatibile con le operazioni di addizione e sottrazione, segue che anche l’ordinamento in Z sopra definito è totale e compatibile con le operazioni estese. Esso rende pertanto Z un → anello ordinato. A differenza di quanto accade in N, la relazione d’ordine definita in Z non è un → buon ordinamento.

Se ≤ è la relazione d’ordine sopra definita, con il simbolo < si indica l’ordinamento stretto associato, definito da x < y se e solo se x ≤ y e x ≠ y. Se x < y, si dice allora che x è minore di y; equivalentemente si scrive anche y > x e si dice che y è maggiore di x. Un numero intero x si dice positivo (rispettivamente non negativo) se x > 0 (rispettivamente se x ≥ 0); si dice invece negativo (rispettivamente non positivo) se x < 0 (rispettivamente se x ≤ 0). L’insieme N dei numeri naturali si identifica allora con l’insieme dei numeri interi non negativi.

In Z vale inoltre la legge di → tricotomia e si definisce la funzione → valore assoluto (o modulo) che associa al numero intero x il numero naturale |x| definito da

Similmente, si definisce il segno di un numero intero non nullo: si dice che un numero intero ha segno + se esso è positivo, si dice invece che ha segno − se esso è negativo. Due numeri interi sono detti concordi se hanno le stesso segno, sono detti invece discordi se hanno segni diversi: equivalentemente due interi sono concordi se e solo se il loro prodotto è un numero positivo, sono discordi se e solo se il loro prodotto è un numero negativo.

Dato un numero intero n, un intero d è detto un divisore di n se esiste un intero m tale che n = d ⋅ m; equivalentemente si dice che d divide n (che, formalmente, si scrive d |n), che n è divisibile per d o che n è un multiplo di d. Le nozioni di multiplo e divisore sono particolarmente importanti per quanto riguarda la struttura algebrica di Z; esse permettono infatti di definire una scomposizione in fattori canonica (→ numero intero, scomposizione in fattori di un) per ogni numero intero diverso da 0, 1 e −1 (→ aritmetica, teorema fondamentale dell’); Z acquisisce così la struttura di → dominio a fattorizzazione unica.

Non tutte le equazioni del tipo bx + a = 0 hanno soluzione in Z: ciò avviene se e solo se a è un multiplo di b. Tale situazione esprime il fatto che Z è un → anello e non un → campo: nessun elemento diverso da 1 e − 1 ammette inverso rispetto alla moltiplicazione. Per risolvere tale tipo di equazioni si introduce l’insieme Q dei numeri razionali, che coincide con il campo dei → quozienti di Z e dove è possibile definire la divisione, operazione inversa della moltiplicazione. Restando nell’ambito dei numeri interi, si può però definire l’operazione di divisione intera, che approssima la divisione (che non è definita in Z) ai numeri interi: per ogni coppia di numeri interi x e y, esistono infatti unici due numeri interi q e r (detti rispettivamente quoziente e resto della divisione di x per y) tali che x = y ⋅ q + r, con 0 ≤ r < |y|.

Il quoziente q coincide con il risultato esatto della divisione se e solo se y divide x, vale a dire se il resto è zero; in caso contrario, q è il numero intero che meglio approssima per difetto il risultato esatto della divisione di a per b, il quale è un numero razionale non intero. La possibilità di definire l’operazione di divisione con resto determina un’ulteriore struttura algebrica su Z, quella di → dominio euclideo.