zeri di una funzione, teorema di esistenza degli

zeri di una funzione, teorema di esistenza degli

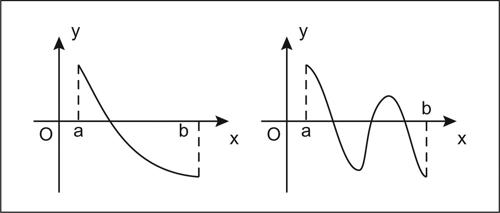
zeri di una funzione, teorema di esistenza degli stabilisce che una funzione continua in un intervallo [a, b], che assume valori discordi agli estremi di tale intervallo, si annulla in almeno un punto interno ad [a, b].

La dimostrazione di tale teorema si ottiene col metodo di → bisezione (dicotomia), ed è quindi costruttiva e particolarmente semplice. I punti in corrispondenza dei quali la funzione si annulla sono detti zeri della funzione (da cui il nome del teorema). Una conseguenza di tale teorema è il teorema dei valori intermedi: una funzione continua in un intervallo [a, b] assume tutti i valori compresi tra il suo minimo e il suo massimo. In altre parole, l’immagine di un intervallo chiuso e limitato è ancora un intervallo chiuso e limitato.