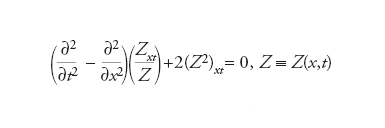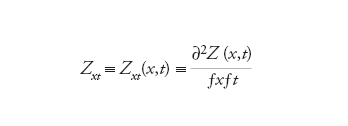zumeroni

zumeroni

Il termine zumerone deriva dall’inglese zoomeron, coniato modificando soliton (solitone) e basandosi sull’analogia con boomeron (bumerone), nonché sul fatto che per l’equazione di riferimento era stata tradizionalmente utilizzata la notazione Z(x,t) come variabile dipendente. Tale termine identifica una particolare soluzione (ovvero una componente di soluzioni più generali) della equazione dello zumerone,

dove le variabili sottoscritte indicano derivate parziali, come, per es.,

Quest’equazione alle derivate parziali, in 1+1 dimensioni (spazio e tempo), è non lineare ma integrabile; essa, in effetti, corrisponde a una riduzione dell’equazione (matriciale) del bumerone. La soluzione Z(x,t) che rappresenta un solo zumerone è localizzata (nel senso che Z_x(x,t) tende a zero per x→±∞) intorno a un punto x=ξ(t) che varia nel tempo, con comportamento bumeronico oppure oscillando periodicamente intorno a un valore finito (comportamento trapponico). Quest’equazione possiede anche soluzioni (che possono essere esibite esplicitamente) di tipo multi-zumeronico, contenenti cioè diversi zumeroni, ciascuno dei quali può avere comportamento bumeronico o trapponico; tali entità interagiscono fra loro nel modo caratteristico dell’equazioni solitoniche (integrabili), cioè riproducendosi se e quando si allontanano l’una dall’altra dopo aver interagito. L’equazione dello zumerone è stata introdotta alla fine degli anni Settanta del Novecento e la sua fenomenologia è stata investigata nell’ambito dello studio delle equazioni non lineari di evoluzione integrabili. Essa è stata successivamente identificata con un’equazione rilevante in geometria differenziale, introdotta quasi un secolo prima in tale contesto dal geometra italiano Pasquale Calapso.

→ Solitoni