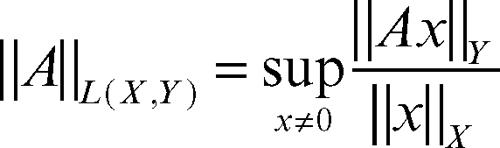Banach, algebra di

Banach, algebra di

Banach, algebra di particolare tipo di algebra (intesa come struttura) associativa su un campo K. Un’algebra associativa X è un’algebra di Banach se è uno spazio di Banach (cioè uno spazio vettoriale normato, con norma ‖...‖_x, e completo rispetto alla distanza indotta dalla norma) per cui vale la disuguaglianza

Un esempio di algebra di Banach è dato dallo spazio L(X, Y) degli operatori lineari limitati tra due spazi di Banach, munito della norma

Un’algebra di Banach può essere commutativa o non commutativa a seconda che sia tale o meno il prodotto interno di cui è dotata l’algebra. Un esempio di algebra di Banach commutativa è dato dall’insieme delle funzioni continue in un cerchio e analitiche all’interno di esso, assumendo come norma il massimo del valore assoluto. Un esempio di algebra di Banach non commutativa è dato dall’insieme degli operatori lineari A continui su uno spazio di Banach (dotati delle usuali operazioni di somma e composizione di funzioni), assumendo come norma ‖A‖ = sup‖Ax‖, con ‖x‖ = 1.

Nella teoria delle algebre di Banach si combinano proprietà algebriche e proprietà topologiche; vi sono inoltre stretti legami tra le algebre di Banach sul campo complesso e le funzioni olomorfe.