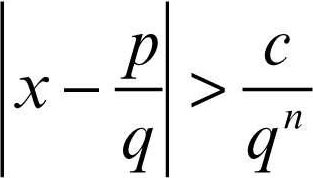Liouville, approssimazione di

Liouville, approssimazione di

Liouville, approssimazione di approssimazione di un numero irrazionale attraverso un numero razionale. In particolare, il teorema di Liouville sull’approssimazione dei numeri algebrici stabilisce che c’è un limite alla possibilità di approssimare un numero algebrico irrazionale per mezzo di un numero razionale. Precisamente, se x è un numero algebrico di grado n ≥ 2 e p e q sono numeri interi qualunque con q > 0, allora esiste una costante positiva c, dipendente soltanto da x, tale che:

Tramite questo teorema, Liouville fu il primo a costruire, nel 1844, un numero trascendente (→ numero algebrico, grado di un; → Liouville, costante di; → irrazionalità, misura di).