asse radicale
asse radicale
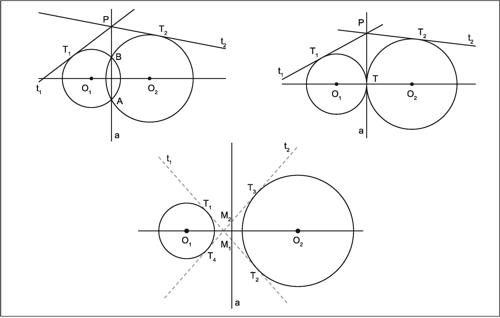
asse radicale (di due circonferenze) retta luogo dei punti tali che i segmenti di tangente condotti da essi alle due circonferenze sono uguali. L’asse radicale è perpendicolare alla retta congiungente i centri delle due circonferenze: se queste si intersecano l’asse radicale è la retta passante per i due punti di intersezione; se le circonferenze sono tangenti è la retta tangente a entrambe nel loro punto di contatto; se sono esterne la retta può essere costruita a partire dalla proprietà che la caratterizza come particolare luogo di punti.
L’asse radicale nel caso di circonferenze esterne è costruito come la retta congiungente i punti medi dei due segmenti di tangenti comuni. Si può seguire anche una → costruzione con riga e compasso particolarmente semplice, tracciando una terza circonferenza qualsiasi c3 che interseca ciascuna delle due circonferenze date, c1 e c2, in due punti; le due rette rispettivamente passanti per ciascuna di queste coppie di punti si intersecano in un punto P; l’asse radicale di c1 e c2 è la retta passante per P e perpendicolare alla congiungente i loro centri.
Nel piano cartesiano, l’asse radicale è la retta di equazione
ottenuta per differenza tra le rispettive equazioni
e
delle due circonferenze date. La retta ottenuta è il luogo dei punti tali che
avendo indicato con P il punto di intersezione delle tangenti a c1 e c2, rispettivamente nei punti T1 e T2. È, quindi, il luogo dei punti che hanno uguale potenza rispetto alle due circonferenze. Questa proprietà vale anche quando le circonferenze sono prive di punti comuni e, quindi, non hanno come intersezione una retta reale. In modo analogo si definisce anche il centro radicale (di tre circonferenze), come quel punto che ha uguale potenza rispetto alle tre circonferenze.