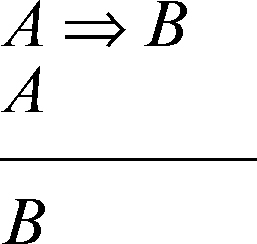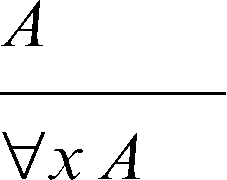predicati, calcolo dei

predicati, calcolo dei

predicati, calcolo dei calcolo logico in cui si può esprimere, in modo rigoroso, un ragionamento e valutarne la correttezza. Se si pensa al ragionamento come a una successione di affermazioni collegate l’una all’altra in modo tale che da alcune premesse si possa giungere a una conclusione, allora il calcolo dei predicati fornisce le regole per costruire ragionamenti sintatticamente corretti. Il vantaggio di disporre di un metodo di calcolo per le deduzioni risiede nel poter applicare il rigore dei procedimenti logico-matematici alle catene di deduzione espresse nel linguaggio naturale. I calcoli logici hanno, però, il limite di non riuscire a cogliere tutta la molteplicità di sfumature dei ragionamenti espressi nel linguaggio naturale; in altri termini il linguaggio naturale non può essere tradotto completamente in un linguaggio formale.

Il calcolo dei predicati viene sviluppato nell’ambito del linguaggio dei predicati e si basa sulle sue formule ben formate (→ predicati, linguaggio dei) che, oltre ai connettivi (presenti anche nel linguaggio degli → enunciati), contengono anche variabili, quantificatori e funzioni. In tale linguaggio formale si definiscono un insieme di assiomi e un insieme di regole di deduzione (o d’inferenza). A partire dagli assiomi e dalle regole si pone il problema di dedurre una formula ben formata A e di controllare la validità di tale deduzione. Il calcolo dei predicati si pone, quindi, come strumento di indagine teorica sul concetto stesso di dimostrazione matematica intesa come derivazione formale da ipotesi. Una derivazione formale di una formula A da un insieme di formule Γ è una sequenza finita di formule A₁, A₂, …, A_n tali che A_n = A e ogni formula A_i sia una delle formule di Γ, un assioma oppure derivi dalle formule precedenti per mezzo dell’applicazione di una regola di inferenza. Nel calcolo dei predicati gli assiomi sono:

a) A ⇒ (B ⇒ A)

b) (A ⇒ (B ⇒C)) ⇒ ((A ⇒ B) ⇒ (A ⇒ C))

c) (¬B ⇒ ¬A) ⇒ ((¬B ⇒ A) ⇒ B)

d) ∀xA ⇒ A(t )

e) ∀x(A ⇒ B) ⇒(A ⇒ ∀xB), se x non è una variabile libera in A.

Nel quarto assioma la lettera t rappresenta un termine e il simbolo A(t ) rappresenta la sostituzione, nella formula A, del termine t al posto della variabile x. Nella sostituzione di t al posto di x occorre fare attenzione a che nessuna variabile libera di t diventi vincolata dopo la sostituzione, cioè che non avvenga la cosiddetta cattura di variabili libere.

Le regole di inferenza del calcolo dei predicati sono (la linea orizzontale indica che dalle premesse al di sopra di essa si deriva la conseguenza sottostante):

• il modus ponens: dalle due premesse, A e A ⇒ B,

si deduce la conclusione B, in formule:

• la generalizzazione: dalla premessa A si deduce la conclusione ∀xA:

Un formula ben formata F, deducibile dagli assiomi attraverso le regole di deduzione, si dice dimostrabile all’interno del calcolo dei predicati e si scrive ⊢ F. La formula ben formata F è, quindi, un teorema della teoria e la sua dimostrazione è la catena di deduzione che va dagli assiomi a F. Il calcolo dei predicati è coerente, cioè in esso non è possibile derivare contraddizioni; quindi, se esiste una deduzione formale di una formula F, non potrà esistere una dimostrazione della formula ¬F. Si noti che i primi tre assiomi del calcolo dei predicati e la regola del modus ponens sono presenti anche nel calcolo formale relativo al linguaggio degli enunciati. Da ciò deriva che tutti i teoremi del calcolo degli enunciati possono essere dimostrati anche nel calcolo dei predicati. Il sistema di assiomi e regole di inferenza presentato non è l’unico possibile per il linguaggio dei predicati. È possibile, per esempio, formalizzare una dimostrazione della logica predicativa anche nel calcolo dei → sequenti, il quale presenta un solo assioma (l’assioma identità) e un insieme più esteso di regole di inferenza. L’uso del calcolo dei sequenti ha il vantaggio di mettere in risalto l’aspetto computazionale del processo di dimostrazione di una formula.

Come nel calcolo degli enunciati, anche per il calcolo dei predicati vale il teorema di deduzione per cui, se Γ è un insieme di formule ben formate e A e B sono due formule ben formate, allora se da Γ e A si deduce B, allora da Γ si deduce A ⇒ B. In formule: se Γ, A ⊢ B allora Γ ⊢ A ⇒ B. Quindi, se dagli assiomi e dalla formula A si deduce B allora A ⇒ B è un teorema nel sistema formale del calcolo dei predicati ed è dimostrabile in esso. Un’altra analogia con il calcolo degli enunciati è il teorema di completezza semantica (→ completezza logica) il quale stabilisce che nel calcolo dei predicati possono essere dimostrate tutte e sole le formule valide (cioè quelle vere in ogni interpretazione del linguaggio dei predicati). In termini più specifici è possibile dimostrare che: a) se una formula F è dimostrabile nel calcolo dei predicati allora F è una formula valida (teorema di correttezza); b) viceversa ogni formula valida è dimostrabile formalmente nel calcolo degli enunciati (teorema di adeguatezza). A differenza del calcolo degli enunciati, il calcolo dei predicati non è decidibile. Un calcolo logico è decidibile se, data una formula ben formata A, esiste un procedimento effettivo che permette di stabilire, in un numero finito di passi, se la formula è dimostrabile o non lo è. Nel calcolo degli enunciati questo procedimento è rappresentato dalle tavole di verità, mentre nel calcolo dei predicati non esiste una procedura simile e quindi, per il teorema di completezza, non esiste un metodo effettivo per controllare se una data formula è logicamente valida oppure no.

Se ci si limita alla quantificazione su variabili individuali, si ha il cosiddetto calcolo predicativo elementare (o del primo ordine); se si ammette anche la quantificazione sulle variabili per predicati o relazioni, si ha il cosiddetto calcolo predicativo del secondo ordine. La differenza tra i due risulta fondamentale sul piano espressivo: le formule del calcolo predicativo del secondo ordine permettono di esprimere importanti nozioni che si dimostrano inesprimibili con il linguaggio del calcolo predicativo elementare.