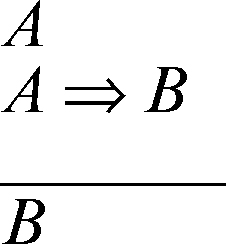proposizioni, calcolo delle
proposizioni, calcolo delle
proposizioni, calcolo delle calcolo logico sviluppato nell’ambito del linguaggio degli → enunciati, detto anche calcolo proposizionale. I suoi oggetti sono le proposizioni, intesi come formule ottenute a partire da proposizioni atomiche tramite l’applicazione dei → connettivi. Le proposizioni atomiche sono indicate con le lettere proposizionali: a, b, c… A esse è attribuito in maniera univoca uno dei due valori di verità: vero o falso. La loro composizione attraverso i connettivi dà luogo a forme proposizionali, che sono → formule ben formate del linguaggio delle proposizioni, espresse con lettere maiuscole A, B, C, …, e il cui valore di verità è calcolabile. Poiché ogni lettera proposizionale è anch’essa una forma proposizionale, queste ultime sono spesso indicate semplicemente come proposizioni, con ciò indicando sia scritture affermative semplici sia quelle ottenute attraverso la loro composizione mediante i connettivi.
Il calcolo delle proposizioni consente di derivare formalmente una forma proposizionale vera da forme proposizionali elementari, assunte come assiomi, attraverso una catena di → deduzione.
Nel calcolo delle proposizioni si possono derivare formalmente tutte le → tautologie, cioè le forme proposizionali sempre vere per ogni valore di verità delle proposizioni atomiche che le compongono. Viceversa si dimostra che ogni forma proposizionale derivabile nel calcolo delle proposizioni è una tautologia (teorema di completezza semantica, in → completezza logica).
La teoria formale assiomatica che esprime il calcolo delle proposizioni si articola in apparato linguistico e apparato deduttivo. L’apparato linguistico (linguaggio delle proposizioni o linguaggio degli enunciati) è costituito dall’alfabeto dei simboli utilizzati nel linguaggio formale e dalle formule ammesse nel linguaggio stesso, dette formule ben formate. I simboli dell’alfabeto sono: le lettere enunciative, le parentesi e i connettivi; è possibile utilizzare solo due connettivi di cui uno sia la negazione (per esempio i connettivi ¬ e ⇒) e ricavare gli altri tramite equivalenze logiche. Le formule ben formate (fbf) sono le forme enunciative costruite a partire dall’alfabeto di simboli, secondo le seguenti regole: a) tutte le lettere enunciative sono fbf; b) se A e B sono fbf lo sono anche (¬A) e (A ⇒ B); c) le fbf sono tutte e sole le forme costruite seguendo queste due regole. L’apparato deduttivo fornisce le regole per costruire una derivazione nel calcolo delle proposizioni ed è composto da → assiomi e regole di → inferenza (o regole di derivazione).
Una volta stabilite tali regole si può definire una derivazione formale di una formula A da un insieme di formule Γ dette ipotesi come una sequenza finita di formule A1A2 … An tali che An = A e ogni formula Ai sia o una delle formule di Γ o un assioma oppure derivi dalle formule precedenti per mezzo dell’applicazione di una regola di inferenza. Nel calcolo delle proposizioni gli assiomi sono:
• A ⇒ (B ⇒ A)
• (A ⇒ (B ⇒ C)) ⇒ ((A ⇒ B) ⇒ (A ⇒ C))
• (¬B ⇒ ¬A) ⇒ ((¬B ⇒ A) ⇒ B)
dove A, B, C sono formule del linguaggio degli enunciati.
L’unica regola di inferenza è il → modus ponens, rappresentato dal seguente schema
dove la linea orizzontale separa le premesse (A e A ⇒ B) dalla conclusione B.
Una fbf F deducibile dagli assiomi attraverso la regola di deduzione si dice dimostrabile all’interno della teoria formale introdotta, si scrive ⊢F e la sua dimostrazione è la catena di → deduzione che va dagli assiomi a F. Il teorema di → deduzione stabilisce che se Γ è un insieme di fbf e A e B sono due fbf, allora se da Γ e A si deduce B, allora da Γ si deduce A ⇒ B. Quindi, se dagli assiomi e dalla fbf A si deduce B allora A ⇒ B è un teorema nel sistema formale del calcolo delle proposizioni ed è dimostrabile in esso.
È importante notare che il calcolo proposizionale, pur essendo semanticamente completo (come stabilito dal teorema di completezza semantica), risulta tuttavia sintatticamente incompleto nel senso che, data comunque una fbf F, non è detto che esista una dimostrazione di F o di ¬F. Si consideri per esempio una lettera enunciativa a: né a né ¬a sono tautologie, quindi nessuna delle due è dimostrabile nel calcolo delle proposizioni.