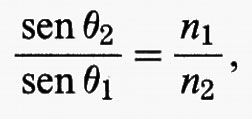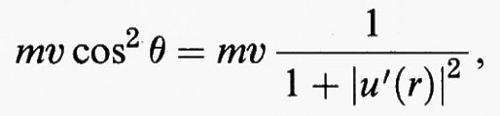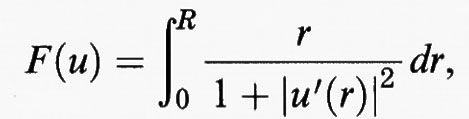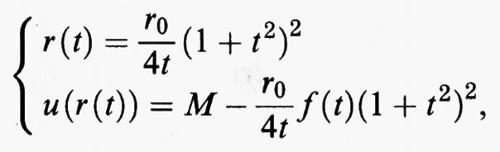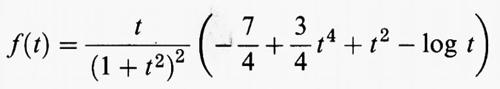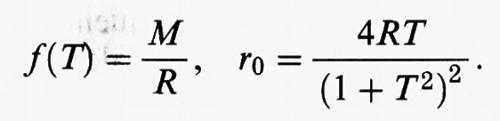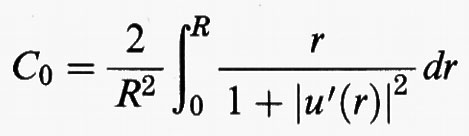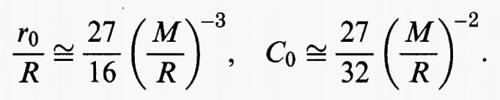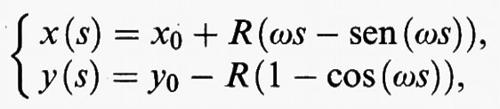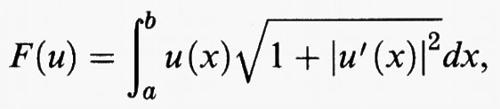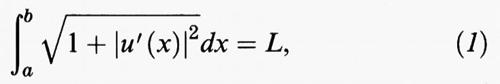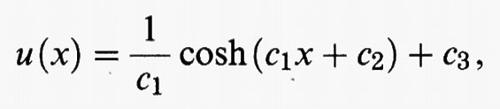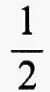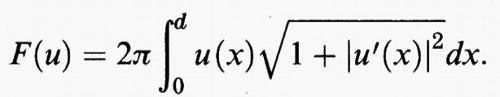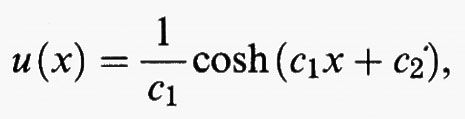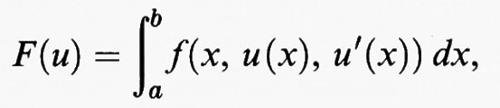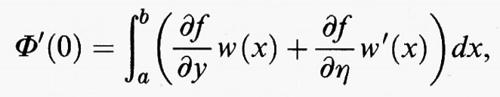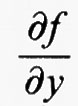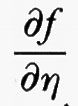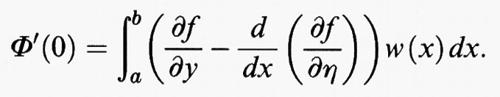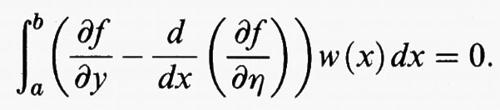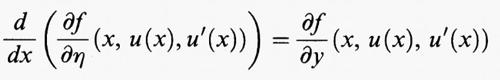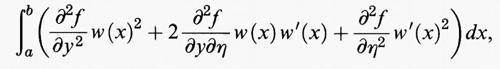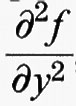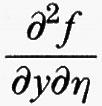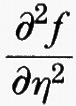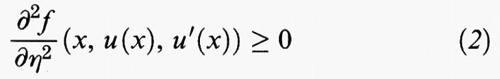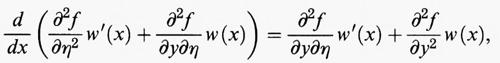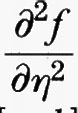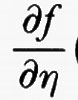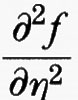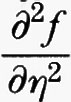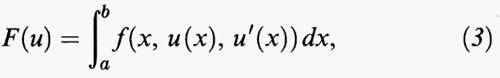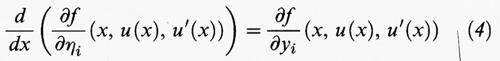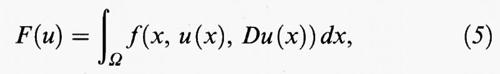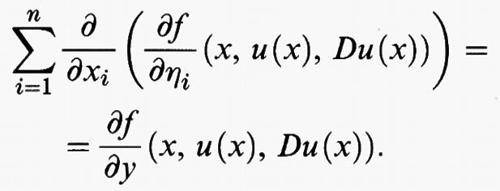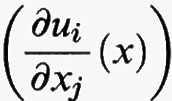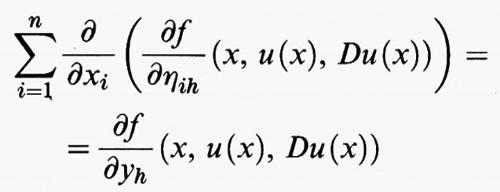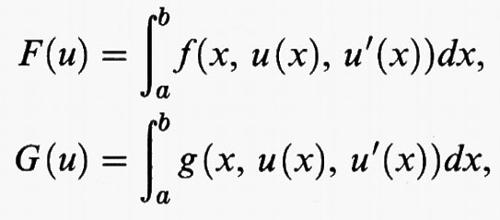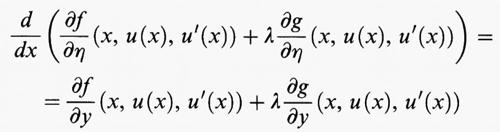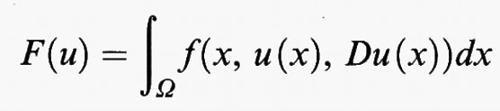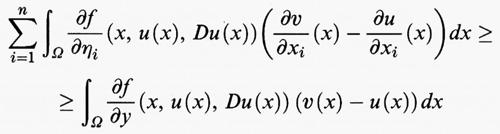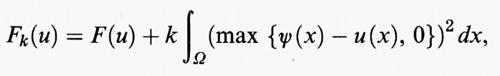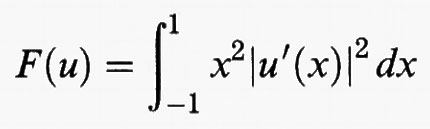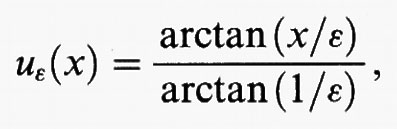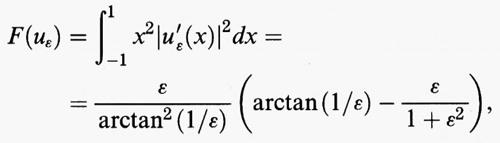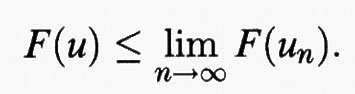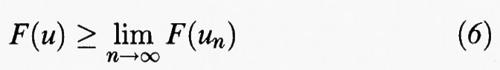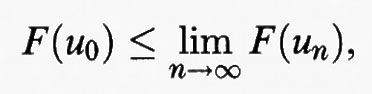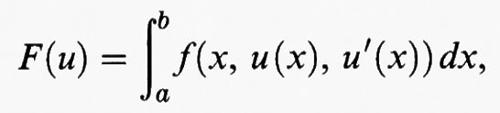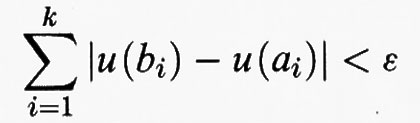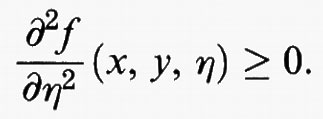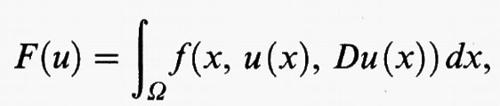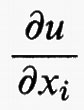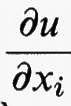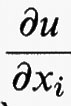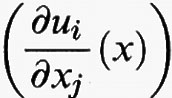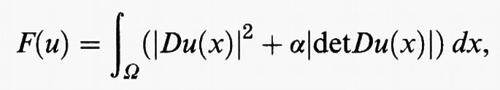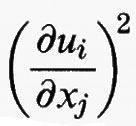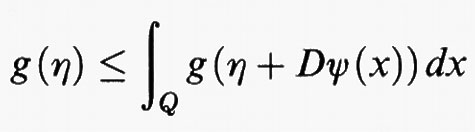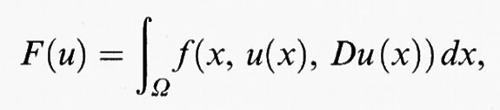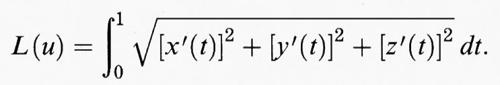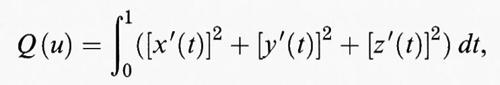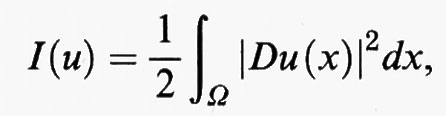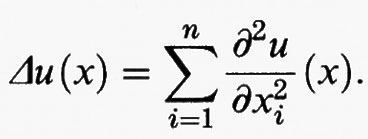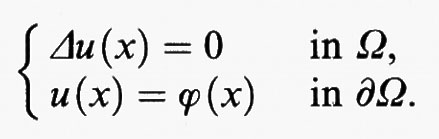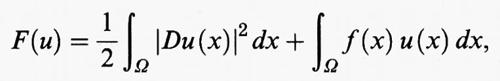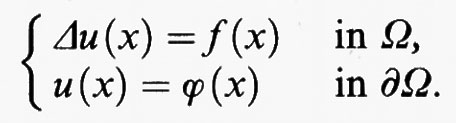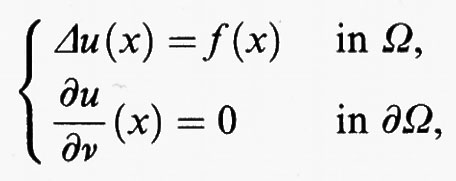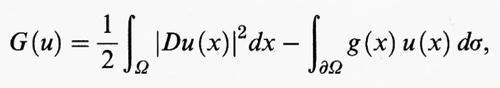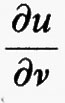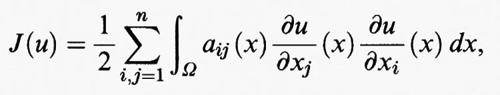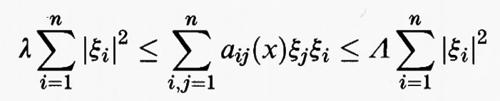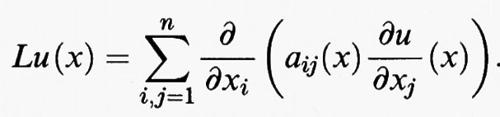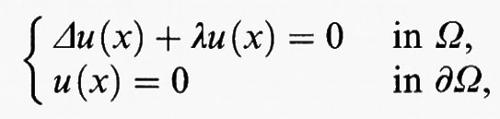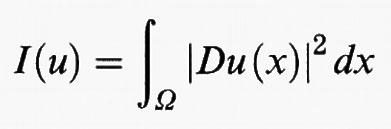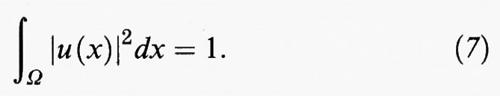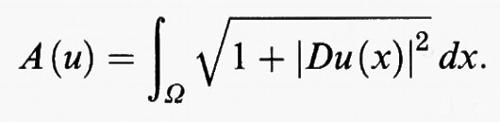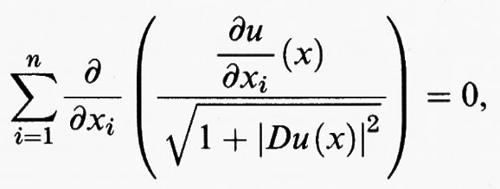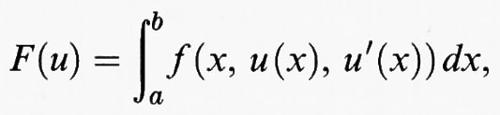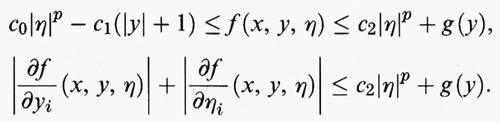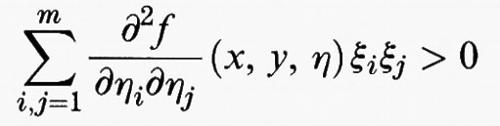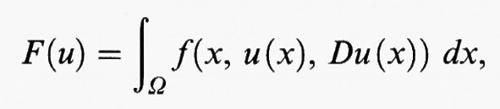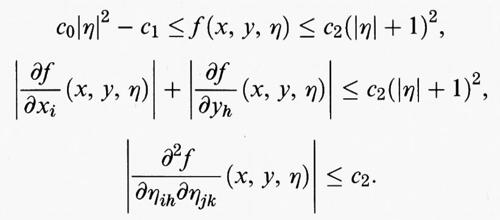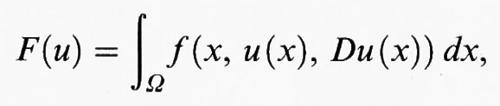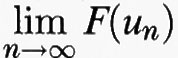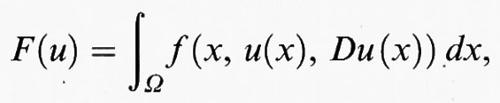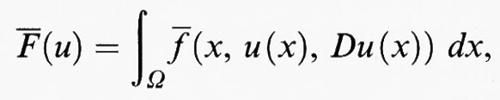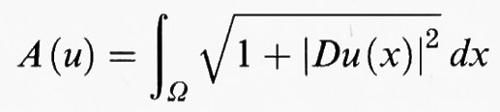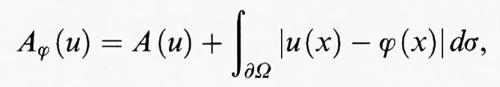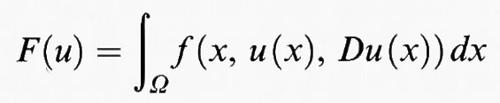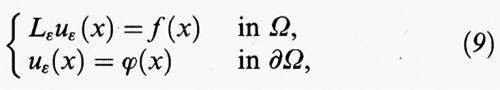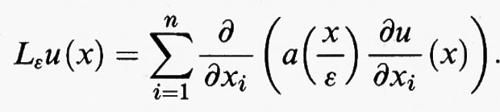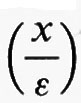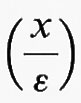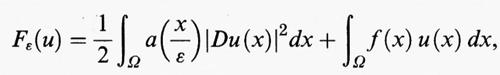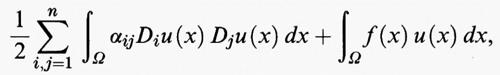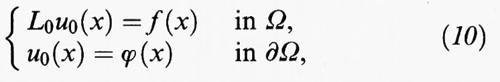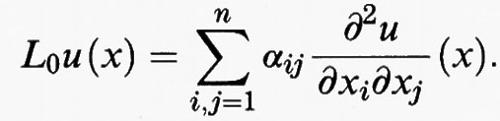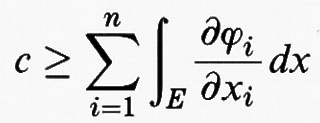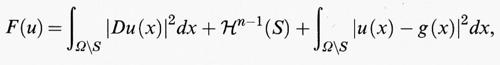Variazioni, calcolo delle

Variazioni, calcolo delle

SOMMARIO: 1. Introduzione.  2. Alcuni esempi storici: a) il problema isoperimetrico; b) il principio di Fermat e le leggi della rifrazione; c) il problema di Newton del profilo di minima resistenza; d) la brachistocrona; e) la catenaria; f) la superficie di rotazione di area minima.  3. Condizioni di minimo per funzionali integrali: a) equazione di Eulero; b) condizioni necessarie di Legendre e di Jacobi; c) condizione necessaria di Weierstrass; d) minimi locali; e) condizione sufficiente di Weierstrass; f) condizione sufficiente di Jacobi; g) il caso vettoriale; h) il caso degli integrali multipli; i) problemi vincolati; l) vincoli unilaterali e disequazioni variazionali.  4. Metodi diretti nel calcolo delle variazioni: a) l'esempio di Weierstrass; b) semicontinuità e metodi diretti; c) teoremi di esistenza per integrali semplici; d) teoremi di esistenza per integrali multipli; e) funzioni quasi convesse.  5. Problemi classici per funzionali integrali: a) geodetiche; b) integrale di Dirichlet e funzioni armoniche; c) autovalori di operatori ellittici; d) superfici cartesiane di area minima.  6. Regolarità delle soluzioni: a) integrali semplici; b) integrali multipli: il caso scalare; c) integrali multipli: il caso vettoriale.  7. Rilassamento e convergenze variazionali: a) rilassamento di problemi di minimo; b) il problema dell'area; c) funzionali a crescita lineare; d) convergenze variazionali e applicazioni.  8. Problemi geometrici: a) superfici minime parametriche; b) frontiere di area minima; c) varietà minime di dimensione arbitraria; d) problemi con discontinuità libera. □ Bibliografia.

1. Introduzione

Il calcolo delle variazioni rappresenta un'area della matematica molto ampia e dai confini piuttosto incerti; in essa rientrano molte questioni sia di matematica pura (per esempio di analisi e geometria), sia di matematica applicata alla fisica, all'ingegneria, alla biologia, all'economia. In tutti questi campi molto è stato fatto, moltissimo probabilmente è ancora da fare, perciò il calcolo delle variazioni è stato paragonato a una foresta da esplorare piuttosto che a un edificio da costruire. Questo articolo non pretende di dare una pianta completa della foresta; vuole solo indicare qualcuna delle strade su cui si sono incamminati esploratori antichi e moderni.

In linea di principio rientrano nel calcolo delle variazioni tutti i problemi in cui si cerca il massimo o il minimo di una data grandezza, dipendente da un certo numero di parametri, che può essere finito o infinito. In molte applicazioni classiche si ha a che fare con grandezze che dipendono da una curva o da una superficie o da una funzione variabile, e quindi il problema della ricerca del minimo non può essere ricondotto all'usuale studio dei minimi di funzioni di un numero finito di variabili reali.

Il calcolo delle variazioni ha interessato in ogni tempo i matematici; nel corso dei secoli i metodi seguiti nello studio dei problemi di calcolo delle variazioni sono stati assai vari, passando da considerazioni sintetiche di geometria classica a un ampio uso del calcolo differenziale e integrale, ai più recenti metodi diretti del calcolo delle variazioni in cui si utilizzano largamente concetti di analisi funzionale - per esempio gli spazi a infinite dimensioni di Hilbert e di Banach - e di moderna teoria della misura, che intervengono, per esempio, nella ricerca delle superfici minime con bordo assegnato.

Un settore assai ampio del calcolo delle variazioni, a cui dedichiamo particolare attenzione, è la ricerca dei minimi di integrali con un integrando che dipende da una funzione variabile e dalle sue derivate; per tali funzionali, oltre alla ricerca dei minimi, ha interesse lo studio dei punti stazionari o punti critici, a cui accenniamo appena, dato che essi sono ampiamente trattati in altri articoli (v. analisi non lineare, vol. VIII; v. analisi non lineare, metodi variazionali, vol. X).

2. Alcuni esempi storici

a) Il problema isoperimetrico.

La più antica versione del problema isoperimetrico consiste nel trovare, tra i poligoni di assegnato perimetro e assegnato numero di lati, quelli di area massima. La soluzione di questo problema è data dai poligoni regolari, cioè dai poligoni aventi lati eguali e angoli eguali. Una dimostrazione di questo risultato, ottenuta unicamente con i metodi sintetici della geometria euclidea, si trova nelle opere di Pappo di Alessandria (circa 320 d.C.), che riportano, sembra, ragionamenti contenuti in un trattato, andato perduto, scritto circa cinque secoli prima da Zenodoro. Questo risultato, insieme a un semplice confronto tra l'area di un cerchio e quella dei poligoni regolari di eguale perimetro, permette di stabilire che il cerchio ha area maggiore di quella di qualsiasi poligono avente lo stesso perimetro. Se si introduce la moderna nozione di lunghezza di una curva rettificabile, con piccole aggiunte tecniche a questi ragionamenti classici si può dimostrare la ‛proprietà isoperimetrica' del cerchio nella forma seguente: la circonferenza racchiude una superficie maggiore di quella delimitata da qualsiasi altra curva piana avente la stessa lunghezza.

Nel trattato di Zenodoro, di cui ci sono giunti solo alcuni frammenti, è enunciata anche l'analoga proprietà della sfera: la superficie sferica racchiude un volume maggiore di quello delimitato da qualsiasi altra superficie chiusa di eguale area. La dimostrazione fornita da Zenodoro è incompleta, e bisognerà attendere fino alla metà del secolo scorso per avere le dimostrazioni moderne a opera di J. Steiner (1842), H. A. Schwarz (1884), H. Minkowski (1903), J. O. Müller (1903) e L. Tonelli (1915), i quali confrontano la sfera con varie classi di superfici più o meno regolari. Successivamente, con i metodi della teoria geometrica della misura, a cui accenneremo sommariamente in seguito (v. cap. 8), è stato possibile attribuire un'area, finita o infinita, a ogni sottoinsieme dello spazio, e dimostrare la proprietà isoperimetrica della sfera rispetto a tutte le superfici chiuse ottenute come bordo di insiemi arbitrari. Questa proprietà è stata poi estesa senza difficoltà al caso di spazi euclidei di dimensione arbitraria.

b) Il principio di Fermat e le leggi della rifrazione.

Nel 1662 P. Fermat enunciò il celebre principio secondo il quale ‟la natura agisce nei modi e mezzi che sono più semplici e rapidi" e non sempre ‟seguendo i cammini più brevi". Nel caso della propagazione della luce, il principio di Fermat stabilisce che i raggi luminosi in un mezzo non omogeneo seguono le traiettorie che rendono minimo il tempo impiegato dalla luce a percorrerle. Tale principio fu applicato da Fermat per ricavare le leggi della rifrazione. Consideriamo due mezzi aventi indici di rifrazione n₁ e n₂ e facciamo l'ipotesi che la velocità della luce in un mezzo sia inversamente proporzionale alla sua densità ottica; se i due mezzi sono disposti come nella fig. 1, il percorso del raggio di luce che congiunge A con B nel minimo tempo risulta essere la spezzata illustrata in fig. 1, in cui

che è appunto l'usuale legge della rifrazione.

La risoluzione di questo problema è fortemente semplificata dal fatto che, per ovvie ragioni geometriche, la traiettoria che fornisce la soluzione deve essere rettilinea nel semipiano superiore e in quello inferiore, e dunque l'unica incognita è la coordinata del vertice della spezzata che giace sulla retta di separazione dei due mezzi. Il problema si riconduce quindi alla ricerca del minimo di una funzione di una variabile reale. Quando invece l'indice di rifrazione varia con continuità, il problema rientra fra quelli del tipo delle geodetiche (v. cap. 5, § a).

c) Il problema di Newton del profilo di minima resistenza.

Nel 1685 Newton formulò e risolse quello che si può considerare il primo vero problema del calcolo delle variazioni: la ricerca del miglior profilo aerodinamico per un corpo che si muove in un fluido non viscoso e incomprimibile. Newton studiò il problema supponendo che il fluido in questione fosse talmente rarefatto da poterlo considerare come composto da piccole particelle uniformemente distribuite e indipendenti tra loro, e che l'interazione tra il corpo in movimento nel fluido e il fluido fosse dovuta soltanto agli urti delle particelle contro il corpo. Inoltre veniva trascurato ogni attrito tangenziale, e si supponeva che il corpo fosse radialmente simmetrico.

In base a queste ipotesi, rappresentando il profilo del corpo mediante il grafico di una funzione u (r), come in fig. 2, si trova che il contributo dell'urto di una particella di massa m al rallentamento del corpo è dato da

dove v è la velocità del corpo e θ è l'angolo indicato in fig. 2. La resistenza complessiva al moto di un corpo avente il profilo descritto dal grafico di una funzione u risulta dunque proporzionale alla quantità

dove R è il raggio della sezione di base del corpo. Se si impone che l'altezza massima del corpo sia M, e che la funzione u sia decrescente, si ottiene che il problema della ricerca del profilo di minima resistenza può essere formulato analiticamente come il problema di minimo per il funzionale F (u) con le condizioni agli estremi u (0) = M, u (R) = 0, e con il vincolo u′ (r) ≤ 0 per ogni r dell'intervallo [0, R]. Vale la pena osservare che, eliminando il vincolo dell'altezza massima assegnata, o quello che impone a u di essere decrescente, si perde l'esistenza del profilo ottimo, in quanto, nel primo caso mediante profili conici sempre più alti, e nel secondo caso mediante profili a zig-zag sempre più fitti, si otterrebbero resistenze F (u) piccole a piacere.

Si dimostra che il problema di minimo considerato sopra ha una soluzione unica u, e che la curva descritta dal punto (r, u (r)) quando r varia tra 0 e R si compone di due parti: un tratto orizzontale del tipo u (r) = M per 0 ≤ r ≤ r₀, e un tratto che può essere scritto in forma parametrica

con 1 ≤ t ≤T. In queste formule la funzione f è data da

e le costanti r_{0 e} T sono determinate dalle condizioni

Ad esempio, con M = R si ottiene il profilo illustrato in fig. 2, in cui r₀/R ≅ 0,35, mentre per la resistenza relativa

si ha la stima approssimata C₀ ≅ 0,37.

È interessante notare che per ogni R e M il profilo ottimo ha comunque una zona piatta in cui u (r) = M; al tendere di M/R verso + ∞ si ottengono le stime asintotiche

d) La brachistocrona.

Il problema della brachistocrona consiste nella ricerca della curva lungo cui far scivolare senza attrito un punto materiale soggetto alla sola azione della forza di gravità, in modo da raggiungere nel minimo tempo un punto assegnato partendo da un altro punto con velocità iniziale nulla. Tale problema fu formulato nel 1638 da Galileo, che propose come curva soluzione un arco di circonferenza. La soluzione esatta, trovata da Johann Bernoulli nel 1697, è invece un arco di cicloide (v. fig. 3).

Per porre il problema in una forma analitica adatta alla sua risoluzione, conviene innanzitutto osservare che ci si può limitare a considerare soltanto le curve giacenti sul piano verticale passante per i punti assegnati. Fissato su tale piano un sistema di coordinate cartesiane in modo che l'asse x sia orizzontale e l'asse y sia verticale, siano (x₀, y₀) e (x₁, y₁) le coordinate dei punti iniziale e finale. Se la curva è descritta in forma parametrica dalle equazioni x = x (s) e y = y (s), con s che varia tra 0 e 1, e si indica con u (s) il punto del piano di coordinate (x (s), y (s)), si trova che il tempo impiegato a percorrere la curva è dato da

dove g è l'accelerazione di gravità, per cui il problema è ricondotto a trovare il minimo di F (u) tra tutte le funzioni regolari u (s) = (x (s), y (s)) verificanti le condizioni agli estremi x (0) = x₀, x (1) = x₁, y (0) = y₀, y (1) = y₁. La soluzione si esprime agevolmente in forma parametrica

dove gli angoli sono misurati in radianti e le costanti R e ω sono determinate dalle condizioni x (1) = x₁ e y (1) = y₁. La curva rappresentata da queste equazioni è una cicloide: si tratta della curva descritta da un punto fissato su una circonferenza (di raggio R) che rotola senza strisciare su una linea retta (nel nostro caso, la retta y = y₀.

e) La catenaria.

Il problema della catenaria - proposto da Galileo nel 1638, e risolto indipendentemente dai fratelli Bernoulli, da Huygens e da Leibniz in una serie di lavori pubblicati tra il 1690 e il 1692 - può essere formulato nella maniera seguente: determinare la forma che un cavo pesante flessibile e inestensibile (catena) assume quando è fissato agli estremi ed è soggetto soltanto all'azione della forza di gravità. Si vede che il cavo si dispone nel piano verticale passante per i suoi punti estremi, A e B. Fissato su tale piano un sistema di coordinate cartesiane in modo che l'asse x sia orizzontale e l'asse y sia verticale, siano (a, α) e (b, β) le coordinate dei punti estremi del cavo pesante. Non è restrittivo supporre a ≤ b. Nel caso banale a = b il cavo si disporrà lungo una linea verticale. Nel caso a 〈 b il profilo del cavo sarà dato dal grafico di una funzione u definita nell'intervallo [a, b]. Si tratta quindi di determinare la forma del cavo, e dunque la relativa funzione u, che rende minima l'energia potenziale del sistema. Si trova che tale energia risulta proporzionale alla quantità

mentre il vincolo di inestensibilità si traduce nell'uguaglianza

dove L è la lunghezza del cavo. Dunque, il problema della catenaria può essere formulato analiticamente come il problema di trovare la funzione u che rende minimo il funzionale F (u) tra tutte le funzioni che verificano le condizioni agli estremi u (a) = α e u (b) = β e soddisfano il vincolo di inestensibilità (1). Si trova che la soluzione è data dalla funzione

rappresentata in fig. 4, dove cosh y è il coseno iperbolico di y definito da cosh y =

(e^y + e^-y), mentre le costanti c₁, c₂, c₃ sono univocamente determinate dalla (1) e dalle condizioni agli estremi.

f) La superficie di rotazione di area minima.

Date due circonferenze nello spazio giacenti su due distinti piani paralleli e disposte in modo tale che la retta a passante per i due centri sia ortogonale ai predetti piani, il problema consiste nel trovare, se esiste, la superficie di area minima tra tutte le superfici di rotazione di asse a aventi per contorno le due circonferenze assegnate. Questo problema fu risolto da Johann Bernoulli e da Leibniz. Si prova che tale minimo esiste quando la distanza tra i due centri è piccola rispetto ai raggi. Altrimenti non esiste il minimo e il limite inferiore delle aree delle superfici di rotazione è dato dalla somma delle aree dei due cerchi.

Per formulare il problema in maniera analitica, fissiamo ad arbitrio un piano contenente la retta a e, su tale piano, fissiamo un sistema di coordinate cartesiane in modo che l'origine sia il centro della prima circonferenza e l'asse x coincida con l'asse di rotazione a. Non è restrittivo supporre che il centro della seconda circonferenza abbia ascissa positiva. Detti r₁ e r₂ i raggi delle due circonferenze e d la distanza dei loro centri, le circonferenze incontreranno il piano nei punti di coordinate (0, ± r₁) e (d, ± r₂). Supponendo che la superficie di rotazione sia generata da una curva esprimibile come grafico di una funzione positiva y = u (x), l'area della superficie di rotazione è data da

Il problema è quindi ricondotto alla ricerca del minimo del funzionale F (u) tra tutte le funzioni u che soddisfano le condizioni agli estremi u (0) = r₁ e u (d) = r₂ le quali traducono la condizione geometrica che le due circonferenze costituiscano il contorno della superficie di rotazione. Questa formulazione analitica è analoga a quella del problema considerato nell'esempio precedente, e il minimo, quando esiste, è dato dalla catenaria

dove le costanti c₁ e c₂ devono essere scelte in modo da soddisfare le condizioni u (0) = r₁ e u (d) = r₂. Dunque la superficie minima di rotazione, quando esiste, è data da una ‛catenoide', ottenuta facendo ruotare una catenaria (v. fig. 5).

Sorge qui un problema nuovo rispetto a quello trattato nell'esempio precedente, dato che per alcuni valori di r₁, r₂ e d non esiste alcuna coppia di costanti c₁, c₂ che soddisfi le condizioni agli estremi, per altri valori vi è una sola coppia, mentre per altri ancora vi sono due coppie. Nei primi due casi il problema di minimo non ha soluzione. Nel terzo caso si hanno due catenoidi, una interna e una esterna, di cui quella esterna ha l'area più piccola. Quest'ultima catenoide fornisce il minimo se e soltanto se la sua area è minore o uguale alla somma delle aree dei due cerchi, e questo è l'unico caso in cui il problema di minimo considerato ammette soluzione. Notiamo che, rispetto ai problemi precedenti, questo problema presenta una novità: non si tratta solo di trovare il minimo, ma si tratta anche di stabilire quando questo minimo esiste. È una situazione che si ripeterà nella maggior parte dei problemi di calcolo delle variazioni moderni, in molti dei quali si riescono a dare solo teoremi di esistenza del minimo e non si trovano rappresentazioni esplicite della soluzione.

3. Condizioni di minimo per funzionali integrali

Gli esempi considerati sopra mostrano che molti classici problemi di calcolo delle variazioni riguardano la ricerca dei minimi di funzionali integrali dipendenti da una funzione e dalle sue derivate prime. Esamineremo ora in dettaglio le principali condizioni di minimalità per questi funzionali, dette anche, con un'espressione più frequente in campo applicativo, condizioni di ottimalità. Vedremo che le funzioni che realizzano il minimo devono soddisfare ben precise condizioni di tipo differenziale (condizioni necessarie di Eulero, di Legendre, di Jacobi e di Weierstrass). Affronteremo anche il problema inverso di stabilire quali soluzioni dell'equazione di Eulero siano punti di minimo del problema considerato, presentando le classiche condizioni sufficienti di ottimalità di Weierstrass e di Jacobi.

a) Equazione di Eulero.

Cominciamo col prendere in esame il caso unidimensionale in cui si considera un funzionale del tipo

dove [a, b] è un intervallo della retta reale R ed f (x, y, η) è una funzione dipendente da tre variabili reali, che supporremo sufficientemente regolare. Fissati due numeri reali α e β, consideriamo il problema di trovare un punto di minimo di F (u) tra tutte le funzioni u sufficientemente regolari che verificano le condizioni agli estremi u (a) = α e u (b) = β. Allo scopo di individuare i punti di minimo, fissata una funzione u, si confronta il valore F (u) con quello ottenuto aggiungendo a u una variazione ammissibile v, valutando in maniera approssimata la differenza F (u + v) - F (u). Il caso più comune è quello in cui si prende v della forma v (x) = εw (x), dove ε è un parametro reale e w è una funzione sufficientemente regolare tale che w (a) = w (b) = 0. Introdotta la funzione di variabile reale Φ (ε) = F (u + εw), la variazione prima di F in u rispetto a w è definita come la derivata prima di Φ in ε = 0. Derivando sotto il segno di integrale si ottiene

dove

e

sono le derivate parziali della funzione f (x, y, η), che si intendono calcolate nei punti (x, y, η) = (x, u (x), u′ (x)). Integrando per parti si ricava

Sia ora u una soluzione del problema di minimo. Poiché la funzione u + εw soddisfa le stesse condizioni agli estremi della u, si ha F (u) ≤ F (u + εw). Dato che questo si verifica per tutti i valori del parametro ε, si conclude che ε = 0 è un punto di minimo della funzione Φ. Da considerazioni elementari di calcolo differenziale risulta che la derivata di Φ si annulla per ε = 0, e dunque la variazione di F in u è uguale a zero per ogni w, cioè

Poiché quest'eguaglianza è valida per ogni funzione sufficientemente regolare w che verifichi w (a) = w (b) = 0, si deduce facilmente che

per ogni punto x dell'intervallo [a, b]. Rispetto alla funzione incognita u questa è un'equazione differenziale ordinaria, in generale non lineare, del secondo ordine, che viene detta ‛equazione di Eulero' associata al problema di minimo. Le sue soluzioni sono chiamate ‛estremali' oppure ‛punti stazionari' o ‛punti critici' del funzionale F. Risulta quindi che, sotto opportune condizioni di regolarità su f, ogni soluzione u sufficientemente regolare del problema di minimo è anche un'estremale. Il contrario in generale non è vero. Dal punto di vista delle applicazioni alla fisica o alla geometria, spesso lo studio dei punti stazionari è importante quanto quello dei punti di minimo. Per esempio, ciò accade quando si applica il principio di Fermat allo studio dei raggi luminosi in un mezzo non omogeneo. In questa trattazione ci occuperemo principalmente dei punti di minimo (per un'esposizione più dettagliata della teoria dei punti critici, v. analisi non lineare, vol. VIII; v. analisi non lineare, metodi variazionali, vol. X).

Un caso particolare in cui ogni soluzione dell'equazione di Eulero è un punto di minimo si presenta quando il funzionale F è convesso, cioè

F (λu + (1 - λ) v) ≤ λ F (u) + (1 - λ) F (v)

per ogni coppia di funzioni u e v e per ogni numero reale λ compreso tra 0 e 1. Se poi il funzionale F è ‛strettamente convesso', cioè la condizione precedente vale con la diseguaglianza stretta quando u è diversa da v, allora il problema di minimo considerato ha al più una soluzione.

b) Condizioni necessarie di Legendre e di Jacobi.

Se u è una soluzione del problema di minimo considerato sopra e se la funzione Φ ammette due derivate, da considerazioni elementari di calcolo differenziale si deduce che la derivata seconda di Φ nel punto 0 è maggiore o uguale a 0. Derivando due volte sotto il segno di integrale si ottiene per Φ″ (0) l'espressione

che considereremo come un nuovo funzionale G (w) dipendente dalla funzione w. Nella formula precedente

,

e

sono le derivate parziali seconde della funzione f (x, y, η) rispetto a y e η, che si intendono calcolate nei punti (x, y, η) = (x, u (x), u′ (x)).

Poiché, per quanto visto sopra, G (w) ≥ 0 per ogni funzione sufficientemente regolare w che verifichi w (a) = w (b) = 0, si deduce facilmente che

per ogni punto x dell'intervallo [a, b]. Questa viene detta condizione necessaria di Legendre.

D'altra parte, essendo G (0) = 0, la funzione identicamente nulla è soluzione del problema di minimo associato a G con condizioni nulle agli estremi. È dunque naturale considerare l'equazione di Eulero del funzionale G, data da

dove, come al solito, le derivate parziali di f sono calcolate in (x, y, η) = (x, u (x), u′ (x)). Si tratta di un'equazione lineare del secondo ordine rispetto alla funzione incognita w. Se

(x, u (x), u′ (x)) > 0 per ogni punto x dell'intervallo [a, b], dalla teoria delle equazioni differenziali ordinarie si deduce che esiste una e una sola soluzione w che soddisfi le condizioni iniziali w (a) = 0 e w′ (a) = 1. I punti in cui tale funzione si annulla si dicono ‛coniugati' ad a. La condizione necessaria di Jacobi asserisce che, se u è un punto di minimo nell'intervallo [a, b], allora non esistono punti c coniugati ad a tali che a 〈 c 〈 b.

c) Condizione necessaria di Weierstrass.

Fissati x₀ e y₀, indichiamo con f₀ la funzione definita da f₀ (η) = f (x₀, y₀, η). L'equazione della retta tangente al grafico di tale funzione nel punto di coordinate (η₀, f₀ (η₀)) è data da:

z = f₀ (η₀) + f′₀ (η₀) (η - η₀).

Si noti che, per definizione di derivata parziale, si ha f′₀ (η) =

(x₀, y₀, η). La funzione ‛eccesso' di Weierstrass, definita da

E (x₀, y₀, η₀, η) = f₀ (η) - f₀ (η₀) - f′₀ (η₀) (η - η₀),

misura dunque quanto il punto di coordinate (η, f₀ (η)) stia al di sopra della predetta retta tangente. Si dimostra, sotto opportune condizioni di regolarità per la funzione f, che ogni punto di minimo u soddisfa la seguente condizione di Weierstrass: E (x, u (x), u′ (x), η) ≥ 0 per ogni punto x dell'intervallo [a, b] e per ogni numero reale η. Ciò significa che, fissato x nell'intervallo [a, b], nel piano (η, z) la retta tangente al grafico della funzione z = f (x, u (x), η) passante per il punto di coordinate (x, f (x, u (x), u′ (x))) sta al di sotto del grafico di tale funzione.

d) Minimi locali.

Accanto alla nozione di punto di minimo (assoluto) conviene introdurre la nozione di minimo locale. Una funzione u si dice un ‛minimo locale forte' per il problema relativo al funzionale F con le condizioni agli estremi u (a) = α e u (b) = β, se soddisfa tali condizioni e se esiste una costante δ > 0 tale che F (u) ≤ F (v) per ogni funzione v sufficientemente regolare che soddisfi le stesse condizioni agli estremi e verifichi inoltre la diseguaglianza ∣^v (x) - u (x) ∣ 〈 δ in ogni punto x dell'intervallo [a, b]. Invece u si dice un ‛minimo locale debole', se soddisfa le condizioni agli estremi e se esiste una costante δ > 0 tale che F (u) ≤ F (v) per ogni funzione v sufficientemente regolare che soddisfi le stesse condizioni agli estremi e verifichi inoltre le diseguaglianze ∣^v (x) - u (x) ∣ 〈 δ e ∣v′ (x) - u′ (x) ∣ 〈 δ in ogni punto x dell'intervallo [a, b]. In altre parole, la funzione u viene confrontata solo con funzioni v che sono ‛vicine' a u, dando alla parola ‛vicino' due significati diversi a seconda che si tratti di minimi locali forti o deboli. È evidente che un minimo locale forte è anche un minimo locale debole, ma non è vero il contrario.

Dal modo con cui si ricavano l'equazione di Eulero e le condizioni necessarie di Legendre e di Jacobi si deduce facilmente che tali condizioni continuano a valere anche per i minimi locali deboli. Invece la condizione necessaria di Weierstrass vale soltanto per i minimi locali forti.

e) Condizione sufficiente di Weierstrass.

Consideriamo ora il problema di stabilire quali soluzioni dell'equazione di Eulero siano punti di minimo locale. Sia u una soluzione dell'equazione di Eulero che soddisfa le condizioni agli estremi. Supponiamo che esista una famiglia a un parametro di estremali i cui grafici riempiono, nel piano (x, y), una regione A intorno al grafico della funzione u, in modo che ogni punto di A stia sul grafico di una e una sola estremale della famiglia. Tale famiglia viene detta ‛campo di estremali'. In questa situazione, a ogni punto (x, y, di A si può associare in maniera univoca la pendenza p = p (x, y) del grafico dell'unica estremale della famiglia passante per (x, y). Questa funzione p (x, y) viene chiamato ‛campo di pendenze' o ‛campo di Weierstrass'. La condizione sufficiente di Weierstrass asserisce che, se sono soddisfatte le condizioni precedenti e se la funzione eccesso di Weierstrass verifica E (x, y, p (x, y), η) ≥ 0 per ogni (x, y) in A e per ogni numero reale η, allora u è un minimo locale forte del problema. Si noti che la condizione su E è sempre verificata se la funzione f (x, y, η) è convessa rispetto alla variabile η, cioè se vale la diseguaglianza

f (x, y, λη₁ + (1 - λ)η₂) ≤ λ f (x, y, η₁) + (1 - λ) f (x, y, η₂)

per ogni x, y, η₁, η₂, e per ogni numero reale λ compreso tra 0 e 1. Se f è sufficientemente regolare, la condizione di convessità rispetto a η è equivalente alla diseguaglianza

(x, y, η) ≥ 0 per ogni (x, y, η).

f) Condizione sufficiente di Jacobi.

Sia u una soluzione abbastanza regolare dell'equazione di Eulero-Lagrange che soddisfa le condizioni agli estremi e la condizione di Legendre (2) con la diseguaglianza stretta. La condizione sufficiente di Jacobi, che si dimostra utilizzando la teoria dei campi estremali di Weierstrass, stabilisce che, se non esistono punti c coniugati ad a tali che a 〈 c ≤ b, allora u è un minimo locale debole del problema. Se, inoltre, la funzione f (x, y, η) è convessa rispetto alla variabile η, allora u è anche un minimo locale forte. Dato che la condizione riguardante i punti coniugati è sempre verificata se l'intervallo [a, b] è sufficientemente piccolo, la condizione sufficiente di Jacobi garantisce la validità del seguente risultato di minimalità in piccolo nel caso di una funzione f sufficientemente regolare verificante la diseguaglianza

(x, y, η) > 0 per ogni (x, y, η): per ogni soluzione u dell'equazione di Eulero si può determinare una costante ε > 0 tale che, se [c, d] è un sottointervallo di [a, b] di ampiezza minore di ε, allora u è un minimo locale forte del corrispondente problema su [c, d] con le condizioni agli estremi individuate da u (c) e u (d), cioè u è un minimo locale forte su intervalli sufficientemente piccoli.

g) Il caso vettoriale.

I risultati visti finora si estendono con ovvie modifiche al caso in cui la funzione u prenda i suoi valori nello spazio euclideo m-dimensionale R^m. In tal caso la funzione u (x) sarà espressa mediante la m-pla delle sue coordinate (u₁ (x), ..., u_m (x)), e la sua derivata u′ (x) sarà data da (u′₁ (x), ..., u′_m (x)). Il funzionale F di cui si cerca il minimo avrà la forma

dove, questa volta, f (x, y, η) è definita per x in [a, b] e per y = (y₁, ..., y_m) e η = (η₁, ..., η_m) in R^m. L'equazione di Eulero diventa allora un sistema di m equazioni differenziali ordinarie nelle m funzioni incognite u₁, ..., u_m

per i = 1, ..., m. Cambiamenti analoghi devono essere fatti nelle condizioni necessarie di Legendre, Weierstrass e Jacobi. La condizione sufficiente di Weierstrass continua a valere purché si modifichi la definizione di campo di Weierstrass aggiungendo una condizione di integrabilità di una opportuna forma differenziale legata alla pendenza, mentre la condizione sufficiente di Jacobi continua a valere con lo stesso enunciato.

Nell'impostazione data da Lagrange (v. fisica, vol. II; v. fisica matematica, vol. II), le equazioni del moto di un sistema meccanico a m gradi di libertà con vincoli olonomi indipendenti dal tempo e soggetto soltanto a forze conservative si esprimono sempre nella forma (4), dove x rappresenta il tempo e la funzione f, detta ‛lagrangiana', è la differenza tra l'energia cinetica e l'energia potenziale del sistema. In questo caso il funzionale (3) viene chiamato ‛azione' del sistema lungo la traiettoria individuata dalla funzione u. I legami visti sopra tra il funzionale e il corrispondente sistema di Eulero (4) permettono di dimostrare il principio di minima azione di Hamilton: la traiettoria seguita da un sistema meccanico è sempre un estremale dell'azione; generalmente è un minimo locale in piccolo, e in molti casi risulta essere un minimo locale in grande, o addirittura un minimo assoluto.

h) Il caso degli integrali multipli.

Nel caso di integrali su regioni Ω dello spazio euclideo n-dimensionale Rⁿ, si considera un funzionale del tipo

dove f (x, y, η) è una funzione definita per x = (x₁, ..., x_n) in Ω, y in R, e η = (η₁, ..., η_n) in Rⁿ. Qui e in seguito Du (x) =

è il gradiente della funzione u e dx = dx₁ ... dx_n indica l'integrazione rispetto alla misura n-dimensionale. Le condizioni agli estremi sono sostituite, in questo caso, da una condizione al contorno, che consiste nell'assegnare una funzione ϕ, definita sul bordo ∂Ω della regione Ω, e nel richiedere che u (x) = ϕ (x) per ogni punto x di ∂Ω. L'equazione di Eulero diventa un'equazione differenziale alle derivate parziali del secondo ordine in Ω, che si scrive

Se invece u prende i suoi valori nello spazio euclideo m-dimensionale R^m, e dunque u (x) = (u₁ (x), ..., u_m (x)), il funzionale F di cui si cerca il minimo avrà ancora la forma (5), ma questa volta Du (x) =

è una matrice di tipo m × n e dunque f (x, y, η) è definita per x in Ω, y in R^m e η nello spazio delle matrici di tipo m × n. L'equazione di Eulero diventa allora un sistema di m equazioni differenziali alle derivate parziali del secondo ordine in Ω nelle m funzioni incognite u₁, ..., u_m, che si scrive in forma sintetica

per h = 1, ..., m.

i) Problemi vincolati.

Torniamo al caso unidimensionale e consideriamo ora due funzionali,

dove [a, b] è un intervallo della retta reale e f (x, y, η) e g (x, y, η) sono due funzioni sufficientemente regolari dipendenti da tre variabili reali. Fissate tre costanti α, β, γ, consideriamo il problema di trovare un punto di minimo di F (u) tra tutte le funzioni u sufficientemente regolari che verificano le condizioni al contorno u (a) = α, u (b) = β e inoltre soddisfano il vincolo G (u) = γ. Si può adattare allo studio di questo problema una variante del metodo dei moltiplicatori di Lagrange e si ottiene che, se u è un punto di minimo del problema e la variazione prima di G in u non è identicamente nulla, allora esiste una costante λ, detta ‛moltiplicatore di Lagrange', tale che

per ogni punto x dell'intervallo [a, b]. Risultati analoghi si ottengono nei casi di dimensione maggiore di uno, o qualora i vincoli siano più di uno.

Una classe di problemi vincolati cui si possono applicare questi metodi è data dai problemi isoperimetrici, in cui si tratta di rendere minimo, o massimo, un funzionale dipendente dalla regione piana racchiusa da una curva, a parità di lunghezza della curva.

l) Vincoli unilaterali e disequazioni variazionali.

Tornando al caso in cui u assume valori reali ed è definita in un dominio Ω dello spazio euclideo n-dimensionale, consideriamo il problema di minimo per il funzionale

con la condizione al contorno u (x) = ϕ (x) su ∂Ω e con la condizione di ostacolo u (x) ≥ ψ (x) in Ω, dove ϕ e ψ sono due funzioni assegnate, sufficientemente regolari, definite rispettivamente su ∂Ω e su Ω. Indichiamo con K l'insieme di tutte le funzioni sufficientemente regolari che soddisfano sia la condizione di ostacolo che la condizione al contorno. In questo caso i ragionamenti che portano all'equazione di Eulero permettono di dimostrare che ogni funzione u che rende minimo il funzionale F su K è anche una soluzione del seguente problema: trovare una funzione u in K che soddisfi la diseguaglianza

per ogni funzione v appartenente a K. Le espressioni di questo genere sono dette ‛disequazioni variazionali'.

Problemi con la condizione di ostacolo intervengono in molte questioni di fisica matematica, ad esempio nello studio dell'equilibrio dei corpi elastici appoggiati a una superficie indeformabile o di altri sistemi meccanici sottoposti a vincoli unilaterali. Lo studio delle disequazioni variazionali è stato approfondito nella seconda metà di questo secolo da vari autori, tra cui ricordiamo G. Fichera, J. L. Lions e G. Stampacchia.

Un metodo molto efficace per approssimare le soluzioni del problema con l'ostacolo ψ, detto metodo di ‛penalizzazione', consiste nel determinare, per ogni intero k, le soluzioni del problema di minimo per il funzionale

con la sola condizione al contorno u (x) = ϕ (x) su ∂Ω. Quando k è grande, la presenza del termine di penalizzazione k ∫_Ω (max {ψ (x) - u (x), 0})² dx ha l'effetto di rendere piccola, per i punti di minimo u_k, la funzione max {ψ (x) + - u_k (x), 0}. Quindi, pur non essendo necessariamente u_k (x) ≥ ψ (x) in ogni punto di Ω, la funzione u_k non può assumere valori molto più piccoli di quelli di ψ. Se il problema con ostacolo ha un'unica soluzione u₀, si può dimostrare che, quando k tende all'infinito, le soluzioni u_k del problema di minimo per F_k convergono verso u₀.

4. Metodi diretti nel calcolo delle variazioni

Fino alla seconda metà del secolo scorso i matematici non si preoccuparono di trovare condizioni generali sotto cui i problemi di minimo considerati nel capitolo precedente ammettano soluzione. Si dava per scontato che una soluzione dovesse esistere, almeno nel caso di funzionali non negativi, e si concentravano gli sforzi sulla determinazione delle condizioni necessarie e sufficienti per i punti di minimo, allo scopo di individuarli esplicitamente o di studiarne le principali proprietà qualitative. Il problema dell'esistenza di un punto di minimo veniva così ricondotto al problema dell'esistenza di una soluzione dell'equazione di Eulero verificante sia le condizioni agli estremi o al contorno, sia una delle condizioni sufficienti considerate nel capitolo precedente. Questo secondo problema, che si esprime in termini di soluzioni di equazioni differenziali, si presenta, in genere, piuttosto arduo, e dunque per questa via si ottengono, di solito, soltanto risposte incomplete.

a) L'esempio di Weierstrass.

Weierstrass fu il primo a mostrare che non sempre un problema di minimo con integrando non negativo ha una soluzione. Il problema proposto da Weierstrass consiste nel cercare il minimo del funzionale

nella classe delle funzioni u dotate di derivata prima continua che soddisfano le condizioni agli estremi u (- 1) = - 1 e u (1) = 1. Osserviamo che su ognuna di queste funzioni si ha F (u) > 0, in quanto, in caso contrario, si avrebbe u′ (x) = 0 in tutti i punti dell'intervallo [- 1, 1] e, di conseguenza, la funzione u sarebbe costante sull'intervallo [- 1, 1], in contrasto con le condizioni agli estremi. Dunque, se esistesse una soluzione u₀ del problema, si avrebbe F (u₀) > 0. Ma, se si considerano le funzioni

che verificano le condizioni al contorno e soddisfano

si ottiene che F (u_ε) tende a 0 quando ε tende a 0. Ne segue che per ε sufficientemente piccolo vale la diseguaglianza F (u_ε) 〈 F (u₀), che contraddice il fatto che u₀ è un punto di minimo.

b) Semicontinuità e metodi diretti.

Dopo l'esempio di Weierstrass, l'attenzione dei matematici fu attirata dal problema dell'esistenza di soluzioni di problemi di minimo per funzionali integrali. I primi risultati in questa direzione furono ottenuti da D. Hilbert nel 1899 per l'integrale di Dirichlet (v. cap. 5, § b). Un impulso notevole alla questione fu dato da L. Tonelli, che estese il metodo di Hilbert a una vasta classe di funzionali integrali. Tonelli osservò che l'esistenza di una soluzione del problema di minimo può essere ottenuta in molti casi utilizzando la nozione di semicontinuità. Dato uno spazio astratto U, con una precisa nozione di ‛convergenza' sulle successioni dei suoi punti, si dice che una funzione F definita su U è ‛semicontinua inferiormente' se, per ogni u in U e per ogni successione u_n in U convergente a u e tale che F (u_n) tenda verso un limite finito o infinito, si ha

Si dice poi che F è ‛coercitiva' se da ogni successione u_n in U con F (u_n) limitata superiormente si può estrarre una sottosuccessione u_nk convergente a un elemento di U.

Servendosi di un classico argomento introdotto da Weierstrass, è molto facile verificare che una funzione semicontinua inferiormente e coercitiva ha almeno un punto di minimo. Infatti, utilizzando le proprietà di completezza del sistema dei numeri reali, è possibile trovare una successione u_n in U, detta ‛successione minimizzante', tale che

per ogni u in U. Usando la coercitività di F si costruisce una sottosuccessione u_nkt di u_n che converge a un elemento u₀ di U. Dalla diseguaglianza di semicontinuità si ottiene

che, insieme alla (6), dà F (u₀) ≤ F (u) per ogni u in U, permettendo di concludere che u₀ è un punto di minimo di F.

I metodi per dimostrare l'esistenza di un punto di minimo di un funzionale integrale basati su questo argomento sono chiamati metodi diretti del calcolo delle variazioni, perché permettono di ottenere direttamente l'esistenza del minimo senza passare attraverso l'equazione di Eulero e le condizioni sufficienti discusse nel capitolo precedente. Per applicare con successo i metodi diretti ai problemi di minimo per funzionali integrali è necessario fissare un insieme U di funzioni ammissibili che tenga conto eventualmente delle condizioni agli estremi o al contorno, e introdurre un'opportuna nozione di convergenza per le funzioni appartenenti a U in modo che il funzionale integrale preso in esame risulti semicontinuo inferiormente e coercitivo.

c) Teoremi di esistenza per integrali semplici.

Tonelli studiò sistematicamente il caso unidimensionale, in cui si considerano funzionali della forma

dove [a, b] è un intervallo della retta reale e f (x, y, η) è una funzione continua dipendente da tre variabili reali, che si suppone derivabile due volte rispetto a η. Lo spazio in cui Tonelli ambientò il problema è lo spazio AC ([a, b]) delle funzioni assolutamente continue su [a, b]. Una funzione u definita sull'intervallo [a, b] si dice ‛assolutamente continua' se per ogni ε > 0 si può trovare un numero δ > 0 tale che

per ogni intero k e per ogni famiglia di k sottointervalli disgiunti [a_i, b_i] di [a, b] tali che la somma delle loro ampiezze sia minore di δ. Notiamo che tutte le funzioni assolutamente continue sono continue e che tutte le funzioni continue e derivabili con derivata prima continua sono assolutamente continue. In base a un classico teorema di H. Lebesgue (1904), la derivata di una funzione assolutamente continua esiste in tutti i punti dell'intervallo di definizione eccettuato, al più, un insieme di punti di misura unidimensionale nulla. La nozione di convergenza impiegata da Tonelli in AC ([a, b]) è l'usuale convergenza uniforme di funzioni continue: u_n converge uniformemente a u se il massimo nell'intervallo [a, b] dello scarto ∣u_n (x) - u (x)∣ tende a zero per n tendente all'infinito.

Supponiamo che esistano un esponente p > 1 e due costanti c₀ > 0 e c₁ > 0 tali che

f (x, y, η) ≥ c₀ ∣ η ∣^p - c₁ (∣y∣ + 1)

e che si abbia

Tonelli dimostrò che il funzionale F è semicontinuo inferiormente sullo spazio AC [(a, b]) rispetto alla convergenza uniforme, e risulta pure coercitivo sull'insieme delle funzioni di u di AC ([a, b]) che soddisfano condizioni agli estremi del tipo u (a) = α e u (b) = β. Ne segue che per ogni coppia di numeri reali α e β il funzionale F (u) ha un punto di minimo nella classe delle funzioni u assolutamente continue su [a, b] che verificano le condizioni agli estremi u (a) = α e u (b) = β.

d) Teoremi di esistenza per integrali multipli.

Per applicare in maniera efficace le stesse idee al caso degli integrali multipli

dove Ω è una regione dello spazio euclideo n-dimensionale Rⁿ, è opportuno utilizzare gli spazi di Lebesgue e di Sobolev. Dato un esponente p ≥ 1, lo spazio di Lebesgue L^p (Ω) è l'insieme delle funzioni u definite su Ω tali che ∣u∣^p sia integrabile (nel senso di Lebesgue) su Ω. La convergenza in L^p (Ω) è definita nel modo seguente: u_n converge a u in L^p (Ω) se l'integrale ∫_Ω ∣ u_n (x) - u (x)∣^p dx tende a zero per n tendente all'infinito.

Si dice che una funzione u di L^p (Ω) ha la derivata parziale ‛debole'

in L^p (Ω) se esiste una funzione v_i di L^p (Ω) tale che

per ogni funzione ψ dotata di derivate parziali continue e nulla fuori di una regione limitata contenuta in Ω e avente distanza positiva dal bordo di Ω. Se tale funzione v_i esiste, essa è univocamente determinata dalla condizione precedente e viene indicata col solito simbolo

Dalle formule di Gauss-Green segue che, se u ha derivate parziali continue, queste ultime coincidono con le derivate parziali deboli. Lo spazio di Sobolev W^1,p (Ω) è l'insieme delle funzioni u in L^p (Ω) aventi derivate parziali deboli

in L^p (Ω) per i = 1, ..., n. Se Ω è abbastanza regolare, è possibile definire la traccia sul bordo ∂Ω di ogni funzione u di W^1,p (Ω). In questo modo ha ancora senso parlare di una condizione al contorno del tipo u (x) = ϕ (x) su ∂Ω, purché i valori di u su ∂Ω siano intesi nel senso delle tracce.

Supponiamo che l'integrando f (x, y, η) sia una funzione semicontinua inferiormente rispetto a (y, η) e convessa rispetto a η. Supponiamo inoltre che esistano un esponente p > 1 e due costanti c₀ > 0 e c₁ > 0 tali che

f (x, y, η) ≥ c₀ ∣ η ∣^p - c₁ (∣y∣ + 1),

dove ∣η∣ indica la norma euclidea del vettore η = (η₁, ..., η_n), definita da ∣η∣ = (Σ_i ∣ η_i ∣²)^1/2. Allora il funzionale F è semicontinuo inferiormente su W^1,p (Ω) rispetto alla convergenza L^p (Ω). In questa forma generale, in cui non viene imposta la continuità di f, questo risultato è stato ottenuto, con diverse dimostrazioni, da C. Olech nel 1976 e da A. D. Ioffe nel 1977. Utilizzando la teoria degli spazi di Sobolev, sviluppata tra gli anni trenta e gli anni cinquanta, si verifica che nelle ipotesi fatte il funzionale F è anche coercitivo rispetto alla convergenza L^p (Ω) sullo spazio delle funzioni u in W^1,p (Ω) aventi traccia assegnata su ∂Ω. Applicando i metodi diretti del calcolo delle variazioni si deduce quindi che, se ∂Ω, è abbastanza regolare e ϕ è la traccia su ∂Ω di almeno una funzione di W^1,p (Ω), allora il funzionale F (u) ha un punto di minimo nella classe delle funzioni u di W^1,p (Ω) che verificano la condizione al contorno u (x) = ϕ (x) su ∂Ω nel senso delle tracce.

e) Funzioni quasi convesse.

I risultati esposti nel paragrafo precedente si estendono senza difficoltà al caso vettoriale, in cui u prende i suoi valori nello spazio euclideo m-dimensionale e, di conseguenza, Du (x) =

è una matrice di tipo m × n. Bisogna però osservare che, mentre nel caso m = 1 il teorema di semicontinuità esposto sopra è ottimale, nel senso che l'ipotesi di convessità della funzione integranda f (x, y, η) rispetto a η è necessaria per la semicontinuità inferiore del funzionale rispetto alla convergenza in L^p (Ω), nel caso m > 1 esistono funzionali integrali, di notevole interesse nella teoria dell'elasticità non lineare, che sono semicontinui inferiormente senza che la funzione integranda sia convessa rispetto alla matrice η = (η_ij). L'esempio più semplice è costituito, nel caso n = m = 2, dal funzionale

dove ∣Du (x)∣2 = Σ_ij

e det Du (x) è il determinante della matrice Du (x). Questo funzionale è semicontinuo inferiormente rispetto alla convergenza L² (Ω) per ogni α > 0, ma non è convesso per α > 2.

Nel caso m > 1, la condizione che sostituisce la convessità e che risulta necessaria e, con certe ipotesi aggiuntive, anche sufficiente per la semicontinuità inferiore dei funzionali integrali, è la cosiddetta ‛quasi convessità', introdotta da C. B. Morrey nel 1952. Una funzione g (η), definita nello spazio delle matrici η = (η_ij) di tipo m × n, si dice quasi convessa se, fissato arbitrariamente un cubo Q n-dimensionale di lato 1, vale la diseguaglianza

per ogni matrice η e per ogni funzione ψ definita su Q, a valori nello spazio euclideo m-dimensionale, nulla sul bordo di Q e dotata di derivate parziali continue.

Ogni funzione convessa risulta quasi convessa, e le due nozioni coincidono se n = 1 oppure m = 1. Una sottoclasse particolarmente interessante di funzioni quasi convesse è costituita dalle funzioni ‛policonvesse', cioè dalle funzioni del tipo g (η) = h (M (ηΠ)), δοξε h è una funzione convessa e M (η) indica il vettore le cui componenti sono i determinanti di tutte le sottomatrici quadrate, dette ‛minori', della matrice η = (gr;g_ij). Ad esempio, se m = n = 2, le funzioni policonvesse sono tutte e solo quelle del tipo

g (η) = h (η₁₁, η₁₂, η₂₁, η₂₂, det η),

con h convessa.

Dopo queste premesse possiamo enunciare ora un teorema di semicontinuità molto generale. A tale scopo indichiamo con W^1,p (Ω; R^m) lo spazio delle funzioni u definite su Ω e a valori nello spazio euclideo m-dimensionale R^m le cui componenti u₁,..., u_m appartengono allo spazio di Sobolev W^1,p (Ω). Le nozioni di convergenza in questo spazio sono date componente per componente. Consideriamo un funzionale del tipo

dove u varia in W^1,p (Ω; R^m) e f (x, y, η) è una funzione continua rispetto a (y, η) e quasi convessa rispetto a η. Supponiamo inoltre che esistano un esponente p > 1 e tre costanti c₀ > 0, c₁ > 0, c₂ > 0 tali che

c₀ ∣ η ∣^p - c₁ (∣y∣ + 1) ≤ f (x, y, η) ≤ c₂ (∣ η ∣ + ∣y∣ + 1)^p,

dove ∣y∣ indica la norma euclidea di y in R^m, mentre ∣η∣ indica la norma euclidea della matrice (η_ij), definita da ∣η∣ = (Σ_ij ∣ η_ij ∣²)^1/2. Allora il funzionale F è semicontinuo inferiormente su W^1,p (Ω; R^m) rispetto alla convergenza L^p (Ω). Questo risultato è stato dimostrato da Morrey nel 1952 nel caso in cui f (x, y, η) sia continua, ed è stato esteso da E. Acerbi e N. Fusco (1984) nel caso in cui f (x, y, η) sia discontinua rispetto a x. La coercitività si dimostra esattamente come nel caso scalare, e dunque, usando i metodi diretti del calcolo delle variazioni, si deduce che, se ∂Ω è abbastanza regolare e ϕ è la traccia su ∂Ω di almeno una funzione di W^1,p (Ω; R^m), allora il funzionale F (u) ha un punto di minimo nella classe delle funzioni u di W^1,p (Ω; R^m) che verificano la condizione al contorno u (x) = ϕ (x) su ∂ΩΠ nel senso delle tracce.

5. Problemi classici per funzionali integrali

a) Geodetiche.

Un classico problema di calcolo delle variazioni di tipo geometrico è il problema delle geodetiche (v. geometria differenziale, vol. III). Data una superficie, si chiama ‛geodetica minimale' un arco di curva sulla superficie la cui lunghezza sia minore o uguale a quella di tutti gli altri archi aventi gli stessi estremi e giacenti sulla superficie. Ad esempio, nel caso di un piano le geodetiche minimali sono i segmenti di retta; nel caso di una superficie sferica, le geodetiche minimali sono gli archi di cerchio massimo che sottendono un angolo al centro minore o uguale a 180°; nel caso di una superficie cilindrica a base circolare, le geodetiche minimali sono gli archi di elica cilindrica che non fanno più di mezzo giro attorno al cilindro, cui vanno aggiunti, come casi limite, i segmenti che giacciono sulle rette generatrici e gli archi di cerchio che giacciono sui piani ortogonali alla direttrice del cilindro e che sottendono un angolo al centro minore o uguale a 180°.

Per estensione, si chiama ‛geodetica' ogni curva su una superficie che abbia la seguente proprietà: dati due punti sulla curva, sufficientemente vicini, l'arco di curva compreso tra questi due punti ha lunghezza minore o uguale a quella di tutti gli altri archi che li congiungono e giacciono sulla superficie. In altre parole, una geodetica è una curva i cui sottoarchi sufficientemente piccoli sono geodetiche minimali. In base a questa definizione, ogni arco di cerchio massimo è una geodetica sulla sfera, mentre solo quelli di ampiezza minore o uguale a 180° sono geodetiche minimali. Allo stesso modo si vede che ogni arco di elica cilindrica è una geodetica sul cilindro, mentre solo gli archi che non si avvolgono per più di mezzo giro sono geodetiche minimali.

Se una curva è descritta in forma parametrica dalle equazioni x = x (t), y = y (t), z = z (t), con t che varia tra 0 e 1, e si indica con u (t) il punto dello spazio di coordinate (x (t), y (t), z (t)), la lunghezza della curva si può esprimere a partire dalla funzione u tramite la classica formula

Dal punto di vista analitico il problema di determinare le geodetiche è quindi ridotto al problema di rendere minimo il funzionale L (u) con opportune condizioni agli estremi e con il vincolo che il punto u (t) giaccia sulla superficie per ogni t nell'intervallo [0, 1].

Il funzionale L (u) ha il vantaggio di essere invariante per cambiamenti di parametro. Se v è un'altra parametrizzazione della stessa curva ottenuta da u mediante la trasformazione v (t) = u (ψ (t)), dove ψ è una funzione regolare e invertibile con funzione inversa regolare, allora L (u) = L (v). D'altra parte questa invarianza implica la non unicità dei punti di minimo e la presenza della radice quadrata impedisce l'applicazione dei metodi diretti visti nel capitolo precedente. Queste difficoltà sono superate utilizzando il funzionale

che ha il vantaggio di dipendere in maniera quadratica dalle derivate. Si può dimostrare che, se [x′ (t)]² + [y′ (t)]² + [z′ (t)]² è costante sull'intervallo [0, 1], allora Q (u) = [L (u)]², mentre altrimenti Q (u) > [L (u)]². Quindi la ricerca del minimo del funzionale L è riconducibile a quella del minimo del funzionale Q, e a quest'ultimo problema si possono applicare sia i metodi diretti per dimostrare l'esistenza di una soluzione, sia le condizioni di Eulero e di Jacobi per caratterizzare i punti di minimo come soluzioni di opportuni sistemi di equazioni differenziali ordinarie.

Tra i risultati più significativi riguardanti le geodetiche ricordiamo che, se due punti di una superficie chiusa possono essere congiunti da una curva che giace interamente sulla superficie, allora possono essere congiunti anche da una geodetica minimale (teorema di Hopf-Rinow, 1931). Questo risultato ha un'estensione naturale al caso di varietà riemanniane di dimensione arbitraria, che costituiscono l'analogo a più dimensioni della nozione di superficie. Altri risultati molto importanti riguardano le geodetiche chiuse. Nel 1917 G. D. Birkhoff dimostrò che su ogni superficie bidimensionale del tipo della sfera c'è almeno una geodetica chiusa. Nel 1929 L. Lyusternik e L. Schnirelmann migliorarono questo risultato dimostrando che su tali superfici vi sono almeno tre geodetiche chiuse senza autointersezioni. L'esistenza di almeno una geodetica chiusa nel caso di varietà riemanniane di dimensione arbitraria fu dimostrata da Birkhoff (1927) nel caso di varietà del tipo della sfera n-dimensionale, e da Lyusternik e A. I. Fet (1951) nel caso generale di varietà compatte. Altri risultati interessanti relativi al numero delle geodetiche congiungenti due punti, anche in presenza di ostacoli, sono stati ottenuti utilizzando strumenti topologici più raffinati (v. analisi non lineare, vol. VIII; v. analisi non lineare, metodi variazionali, vol. X).

b) Integrale di Dirichlet e funzioni armoniche.

Un classico problema di calcolo delle variazioni per integrali multipli riguarda l'integrale di Dirichlet

dove Ω è un dominio limitato dello spazio euclideo a n dimensioni con bordo ∂Ω sufficientemente regolare. C'è uno stretto legame tra l'integrale di Dirichlet e l'operatore di Laplace

Infatti l'equazione di Laplace

Δu (x) = 0 in Ω,

le cui soluzioni sono dette funzioni armoniche, è l'equazione di Eulero relativa all'integrale di Dirichlet. Poiché tale funzionale è convesso, fissata una funzione sufficientemente regolare ϕ definita su ∂Ω, risulta che una funzione u è soluzione del problema di minimo per l'integrale di Dirichlet con la condizione al contorno u (x) = ϕ (x) su ∂Ω se e solo se u è soluzione del problema di Dirichlet per l'equazione di Laplace

Questa equivalenza fu usata da Hilbert nel 1899 per dare la prima dimostrazione rigorosa dell'esistenza della soluzione del problema di Dirichlet nel caso di dominî limitati e uniformemente convessi del piano con bordo sufficientemente regolare.

Qualora l'integrale di Dirichlet sia sostituito dal funzionale

dove f è una funzione definita su Ω, la corrispondente equazione di Eulero è l'equazione di Poisson

Δu (x) = f (x) in Ω,

che compare in moltissimi problemi di fisica matematica riguardanti mezzi lineari omogenei e isotropi, tra cui ricordiamo i problemi di elettrostatica, di campi gravitazionali e di equilibrio di membrane elastiche. Risulta quindi che una funzione u è soluzione del problema di minimo per il funzionale F con la condizione al contorno u (x) = ϕ (x) su ∂Ω se e solo se u è soluzione del problema di Dirichlet per l'equazione di Poisson

Nel caso in cui si consideri un punto di minimo del funzionale F senza fissare condizioni al contorno, si dimostra che una funzione u è un punto di minimo del funzionale F se e solo se u è soluzione del seguente problema:

dove ν è il vettore di lunghezza unitaria ortogonale a ∂Ω nel punto x e diretto verso l'esterno di Ω, mentre

(x) è la derivata della funzione u nella direzione del vettore ν. Si noti che la condizione al contorno

(x) = 0, detta ‛condizione di Neumann omogenea', che compare nell'equazione di Eulero, non è stata imposta nel problema di minimo; essa è conseguenza del fatto che u è soluzione di un problema di minimo senza dati al contorno. Condizioni di questo tipo sono chiamate condizioni al contorno ‛naturali'. Affinché il funzionale F abbia un punto di minimo, e dunque il problema di Neumann omogeneo abbia una soluzione, è necessario e sufficiente che la funzione f abbia valor medio nullo su Ω.

Se si considera il funzionale

dove g è una funzione definita su ∂Ω e dσ indica l'integrazione rispetto alla misura superficiale (n - 1)-dimensionale, si ottiene che una funzione u è un punto di minimo del funzionale G se e solo se u è soluzione di questo problema:

In questo caso la condizione al contorno naturale

(x) = g (x) viene detta ‛condizione di Neumann non omogenea'. Affinché il funzionale G abbia un punto di minimo è necessario e sufficiente che g abbia media nulla su ∂Ω.

Tutti questi risultati si estendono facilmente al caso in cui l'integrale di Dirichlet sia sostituito dal funzionale

dove (a_ij (x)), i, j = 1, ..., n, è una matrice di funzioni definite su Ω, con a_ij (x) = a_ji (x), che soddisfa le seguenti condizioni di ellitticità e di limitatezza: esistono due costanti λ > 0 e Λ > 0 tali che

per ogni x in Ω e per ogni ξ = (ξ₁, ..., ξ_n) in Rⁿ. In tal caso l'operatore di Laplace è sostituito dall'operatore ellittico L definito da

La corrispondente equazione

Lu (x) = f (x) in Ω

compare in luogo dell'equazione di Poisson in moltissimi problemi di fisica matematica riguardanti il comportamento di mezzi lineari non omogenei e non isotropi.

La nozione di integrale di Dirichlet può essere estesa al caso in cui u sia una funzione definita su una varietà riemanniana e prenda i suoi valori in un'altra varietà riemanniana. In tal caso i punti stazionari sono le mappe armoniche tra le due varietà, il cui studio è legato a interessanti questioni di topologia e di geometria differenziale.

c) Autovalori di operatori ellittici.

Il problema degli autovalori per l'operatore di Laplace Δ con condizioni al contorno di Dirichlet omogenee in un dominio limitato Ω dello spazio euclideo n-dimensionale consiste nel determinare quei valori del parametro λ, detti ‛autovalori', per i quali il problema

ha soluzioni u non identicamente nulle, dette ‛autofunzioni'. Questo problema ha molteplici applicazioni in fisica matematica, tra cui menzioniamo il metodo di risoluzione delle equazioni del calore e delle onde mediante sviluppi in serie.

Il problema degli autovalori è strettamente legato al problema di rendere minimo l'integrale di Dirichlet

tra tutte le funzioni sufficientemente regolari u che si annullano sul bordo di Ω e che soddisfano il vincolo

Usando il metodo dei moltiplicatori di Lagrange si ricava facilmente che il valore minimo del predetto problema vincolato coincide con il più piccolo degli autovalori, e che le corrispondenti autofunzioni sono date dai multipli, per costanti non nulle, delle funzioni che realizzano il minimo. Le autofunzioni corrispondenti agli altri autovalori coincidono, a meno di un fattore moltiplicativo non nullo, con i punti critici del funzionale I (u) soggetto al vincolo (7) e a condizioni di Dirichlet omogenee, mentre i corrispondenti autovalori sono dati dai valori assunti dal funzionale I (u) in tali punti critici.

La teoria di Riesz-Fredholm permette di stabilire che gli autovalori possono essere ordinati in una successione crescente (λ_j) che tende a + ∞, e che ogni funzione sufficientemente regolare può essere espressa come somma di una serie di autofunzioni. Ciò consente di ricavare le soluzioni delle equazioni del calore e delle onde come somme di serie i cui termini sono costruiti a partire dagli autovalori e dalle autofunzioni dell'operatore di Laplace (v. equazioni funzionali, vol. II). Risultati del tutto analoghi si ottengono nel caso di condizioni al contorno di Neumann, oppure qualora l'operatore di Laplace sia sostituito da un operatore ellittico L del tipo considerato nel paragrafo precedente.

d) Superfici cartesiane di area minima.

Se Ω è una regione limitata del piano e u è una funzione definita su Ω e dotata di derivate parziali continue, il grafico di u è una superficie regolare la cui area è data da

Una superficie di questo tipo si dice superficie cartesiana. Fissata una funzione ϕ definita sul bordo ∂Ω di Ω, il problema di minimo per il funzionale A (u) con le condizioni al contorno u (x) = ϕ (x) su ∂Ω viene detto problema dell'area minima in forma cartesiana. Esso corrisponde al problema geometrico di trovare la superficie cartesiana di area minima tra quelle che hanno per contorno il grafico della funzione ϕ. È importante notare che la richiesta che la superficie minima sia di tipo cartesiano, cioè sia rappresentabile come grafico di una funzione, pone forti limitazioni geometriche su ∂Ω e sul dato ϕ. Ad esempio, se Ω è una corona circolare e ϕ è costante in ciascuna delle due circonferenze che costituiscono il bordo di Ω, si può dimostrare che esiste la superficie cartesiana di area minima se le costanti sono abbastanza vicine, e che non esiste se sono troppo lontane. Se invece Ω è una regione piana uniformemente convessa e ϕ è sufficientemente regolare, si può dimostrare che il problema dell'area minima in forma cartesiana ha una e una sola soluzione. La prima dimostrazione di questo risultato fu ottenuta da A. Haar nel 1927, utilizzando il metodo impiegato da Hilbert per l'integrale di Dirichlet. Nel caso in cui Ω sia una regione dello spazio euclideo a n dimensioni, il funzionale A (u) conserva ancora il significato geometrico di area n-dimensionale del grafico della funzione u, che è, in questo caso, una varietà regolare di dimensione n immersa in uno spazio euclideo di dimensione n + 1. L'estensione del teorema di Haar al caso n-dimensionale è dovuta a M. Miranda (1965). Utilizzando metodi più raffinati, H. Jenkins e J. Serrin (1968) hanno dimostrato che è possibile alleggerire le ipotesi geometriche sul dominio Ω e le ipotesi di regolarità sulla funzione ϕ. Ritorneremo su questo problema nel caso di dominî generali nel cap. 7.

L'equazione di Eulero del funzionale A (u) è l'equazione delle superfici minime:

la quale esprime la proprietà geometrica che il grafico di u ha curvatura media nulla (v. geometria differenziale, vol. III). Essendo A (u) un funzionale convesso, c'è completa equivalenza tra l'essere soluzione dell'equazione delle superfici minime con assegnate condizioni al contorno e l'essere soluzione del problema dell'area minima in forma cartesiana con le stesse condizioni al contorno.

Un'importante proprietà di questa equazione è il teorema di Bernstein: se u è una soluzione dell'equazione delle superfici minime definita in tutto il piano, allora il grafico della funzione u è un piano. Dopo la dimostrazione di S. Bernstein (1915) rimase per lungo tempo aperto il problema di stabilire se un risultato analogo fosse valido in spazi di dimensione maggiore. Precisamente si trattava di stabilire se ogni soluzione u dell'equazione delle superfici minime definita in tutto lo spazio euclideo n-dimensionale ha per grafico un iperpiano, cioè ha la forma u (x) = a₀ + a₁ x₁ + ... + a_n x_n per opportune costanti a₀, a₁, ..., a_n. Nel 1965 E. De Giorgi dimostrò che questa proprietà vale anche per n = 3, e l'anno seguente F. J. Almgren estese questo risultato al caso n = 4. Nel 1968 J. Simons ottenne una dimostrazione per n ≤ 7. Un controesempio dovuto a E. Bombieri, E. De Giorgi ed E. Giusti (1969) mostrò invece che il teorema di Bernstein non è vero se n ≥ 8.

6. Regolarità delle soluzioni

Una volta trovata, in un opportuno spazio di funzioni, la soluzione di un problema di minimo per un funzionale integrale, è naturale chiedersi se questa soluzione sia più regolare quando i dati del problema sono più regolari.

a) Integrali semplici.

Nel caso degli integrali su un intervallo [a, b] della retta reale, la risposta al problema della regolarità è legata, tramite l'equazione di Eulero, alla teoria classica delle equazioni differenziali ordinarie. Possiamo considerare subito il caso in cui u prende i suoi valori nello spazio euclideo m-dimensionale R^m, visto che, nel caso di integrali su un intervallo unidimensionale, ciò non presenta ulteriori difficoltà rispetto al caso scalare. Sia dunque F un funzionale del tipo

dove f (x, y, η) è una funzione definita per x in [a, b] e per y = (y₁, ..., y_m) e η = (η₁, ..., η_m) in R^m. Supponiamo che f sia di classe C^∞, cioè sia dotata di derivate parziali continue di ogni ordine. Supponiamo inoltre che esistano un esponente p > 1, tre costanti c₀ > 0, c₁ > 0, c₂ > 0 e una funzione continua g tali che

Supponiamo infine che valga la seguente condizione, leggermente più forte dell'ipotesi di convessità rispetto alla variabile η:

per ogni x in [a, b] e per ogni y, η, ξ in R^m. Allora il problema di minimo per F con assegnate condizioni al contorno ammette almeno una soluzione u, e tutte le soluzioni sono funzioni di classe C^∞ sull'intervallo [a, b].

b) Integrali multipli: il caso scalare.

Il problema della regolarità è molto più complesso nel caso degli integrali multipli, cioè degli integrali su un dominio Ω dello spazio euclideo n-dimensionale Rⁿ. In questo caso c'è una notevole differenza tra i problemi scalari, in cui l'incognita u prende valori reali, e quelli vettoriali, in cui prende valori in uno spazio euclideo di dimensione maggiore di uno. Cominciamo con l'esaminare il caso scalare, considerando un funzionale della forma

dove f (x, y, η) è una funzione di classe C^∞ definita per x = (x₁, ..., x_n in Ω, y in R e η = (η₁, ..., η_n) in Rⁿ. Supponiamo che esistano tre costanti c₀ > 0, c₁ > 0, c₂ > 0 tali che

Supponiamo inoltre che valga la seguente condizione, più forte dell'usuale ipotesi di convessità rispetto alla variabile η:

per ogni x in Ω, per ogni y in R e per ogni η, ξ in Rⁿ. Allora il problema di minimo per F con assegnate condizioni al contorno abbastanza regolari ammette almeno una soluzione u, e tutte le soluzioni sono funzioni di classe C^∞ sul dominio Ω. Questo risultato, conseguenza del teorema di hölderianità di De Giorgi e J. Nash per soluzioni di equazioni ellittiche lineari, è stato dimostrato nel 1957, mentre l'estensione, a opera di vari autori, al caso in cui l'esponente 2 sia sostituito da un esponente p ≠ 2 è di poco successiva.

c) Integrali multipli: il caso vettoriale.

Nel caso vettoriale, in cui u (x) = (u₁ (x), ..., u_m (x)), i risultati di regolarità appena esposti non sono veri. Il primo esempio di funzionale regolare che ammette punti di minimo discontinui fu trovato da E. Giusti e M. Miranda nel 1968. È comunque possibile, sotto opportune ipotesi, ottenere dei risultati di regolarità parziale, cioè dimostrare che la soluzione è regolare in un sottoinsieme di Ω abbastanza grande. A titolo di esempio, consideriamo un funzionale del tipo

dove f (x, y, η) è una funzione di classe C^∞ definita per x in Ω, y in R^m e η nello spazio delle matrici di tipo m × n. Se f soddisfa ipotesi simili a quelle considerate nel paragrafo precedente per il caso scalare, il problema di minimo per F con assegnate condizioni al contorno abbastanza regolari ammette almeno una soluzione u, e tale soluzione è una funzione di classe C^∞ in un sottoinsieme Ω₀ di Ω, con la proprietà che la differenza S = Ω Ω₀ ha misura n-dimensionale nulla. Questi e altri risultati di questo tipo, in cui l'esponente 2 è sostituito da un esponente p ≠ 2, sono stati ottenuti a partire dalla fine degli anni settanta e sono stati estesi nel corso degli anni ottanta a particolari classi di integrandi quasi convessi.

Se, in aggiunta alle ipotesi precedenti, si suppone anche che f sia quadratica rispetto a η, cioè

allora si può dimostrare che l'insieme singolare S ha misura (n - 2)-dimensionale nulla e, sotto ipotesi ancor più particolari, verificate ad esempio nei problemi legati alle mappe armoniche, è possibile mostrare che S ha dimensione n - 3.

7. Rilassamento e convergenze variazionali

a) Rilassamento di problemi di minimo.

Se il funzionale F non è semicontinuo inferiormente, i metodi diretti del calcolo delle variazioni non sono applicabili al problema della ricerca di un punto di minimo; in tal caso è spesso utile considerare il più grande funzionale semicontinuo inferiormente che sia minore o uguale a F, che indicheremo con Å e chiameremo ‛funzionale rilassato' associato a F. Detto U lo spazio, dotato di un'opportuna nozione di convergenza, su cui è definito F, il valore Å (u) su un generico elemento u di U è caratterizzato dalle seguenti proprietà: 1) per ogni successione u_n in U convergente a u e tale che F (u_n) tenda verso un limite, finito o infinito, si ha Å (u) ≤

2) esiste una successione v_n in U convergente a u e tale che Å (u) =

Se F è coercitivo, anche Å risulta coercitivo. Dunque, applicando i metodi diretti del calcolo delle variazioni a Å, si ottiene facilmente l'esistenza di una soluzione del problema rilassato.

Ricordiamo che una successione u_n in U è detta successione minimizzante per F se F (v) ≥

F (u_n per ogni v in U. Il legame tra i punti di minimo di Å e le successioni minimizzanti di F è dato dalle seguenti proprietà: 1) per ogni punto di minimo u di Å esiste una successione minimizzante u_n per F che converge a u; 2) se v_n è una successione minimizzante per F che converge a un elemento v di U, allora v è un punto di minimo del problema rilassato. Il problema di minimo per Å viene detto ‛problema rilassato' associato a F, e le sue soluzioni sono spesso chiamate ‛soluzioni deboli' o ‛soluzioni rilassate'; pur essendo, a volte, alquanto irregolari, esse hanno il pregio di esistere sotto ipotesi molto generali e forniscono informazioni importanti sul comportamento del problema di minimo originale.

Per meglio comprendere il procedimento di rilassamento consideriamo ad esempio un funzionale integrale del tipo

dove Ω è una regione dello spazio euclideo n-dimensionale e f (x, y, η) è una funzione continua verificante le disuguaglianze c₀ ∣ η ∣^p ≤ f (x, y, η) ≤ c₁ (∣ η ∣ + ∣y∣ + 1)^p per opportune costanti c₀ > 0, c₁ > 0, p > 1. Non avendo imposto alcuna condizione di convessità su f (x, y, η) rispetto a η, in generale il funzionale F non risulterà semicontinuo inferiormente rispetto alla convergenza L^p (Ω) e il problema di minimo associato, con condizioni fissate al contorno, potrà non avere soluzione. In tal caso si trova per il funzionale rilassato Å l'espressione

dove å (x, y, η) rappresenta la massima funzione convessa rispetto a η (quasi convessa rispetto a η nel caso di funzioni u a valori in R^m) che sia minore o uguale a f (x, y, η). Il problema di minimo per Å ammette dunque soluzione e le successioni minimizzanti del funzionale originale F risulteranno vicine, nel senso della distanza di L^p (Ω), alle soluzioni del problema rilassato.

b) Il problema dell'area.

Un altro problema in cui il rilassamento fornisce una descrizione qualitativa del comportamento delle soluzioni, o delle successioni minimizzanti, è il problema dell'area minima in forma cartesiana di cui si è discusso nel cap. 5, § d. Data una regione Ω dello spazio euclideo a n dimensioni, che supporremo limitata e regolare, e una funzione regolare ϕ definita su ∂Ω, il problema consiste nel trovare il minimo per il funzionale dell'area

nella classe delle funzioni u coincidenti con ϕ su ∂Ω. Si è già visto che questo problema non sempre ammette soluzione.

Il corrispondente problema rilassato (rispetto alla convergenza L¹ (Ω)) è il problema di minimo per il funzionale

dove dσ indica l'integrazione rispetto alla misura superficiale (n - 1)-dimensionale. Si noti che nel problema rilassato, che ammette sempre soluzione, la funzione u non è più vincolata ad assumere il dato ϕ su ∂Ω. Se Ω è uniformemente convesso o, più in generale, soddisfa le condizioni del teorema di Jenkins e Serrin, allora il punto di minimo di A_ϕ è unico e coincide con ϕ su ∂Ω. Se invece Ω non soddisfa tali condizioni, vi sono dei casi, come quello della corona circolare considerato nel cap. 5, in cui il punto di minimo u di A_ϕ non coincide con ϕ su una parte della frontiera di Ω. In tal caso il grafico delle funzioni di una successione minimizzante per il problema dell'area tende a essere verticale vicino ai punti di ∂Ω su cui u (x) ≠ ϕ (x). Il funzionale A_ϕ (u) ha il seguente significato geometrico: esso rappresenta l'area (n - 1)-dimensionale della superficie costituita dall'unione del grafico della funzione u con la superficie verticale costituita dai punti di coordinate (x₁, ..., x_n, t) con x = (x₁, ..., x_n in ∂Ω e t compreso tra u (x) e ϕ (x). L'unione di queste due superfici rappresenta, in un certo senso, il limite geometrico dei grafici di una successione minimizzante.

c) Funzionali a crescita lineare.

Il metodo del rilassamento si adatta molto bene allo studio di funzionali integrali

con crescita lineare, in cui l'integrando è continuo e verifica le diseguaglianze

c₀ (∣η∣ - 1) ≤ f (x, y, η) ≤ c₁ (∣η∣ + ∣y∣ + 1) (8)

per opportune costanti c₀ > 0 e c₁ > 0. Il caso modello è costituito dal funzionale dell'area A (u) considerato nel paragrafo precedente.

Per i funzionali a crescita lineare i teoremi di esistenza visti nel cap. 4 non si applicano, in quanto l'ipotesi p > 1 è essenziale per la coercitività nello spazio di Sobolev W^1,p (Ω). Facili esempi mostrano che la soluzione, in generale, non può essere trovata nello spazio di Sobolev W^{1, 1} (Ω). Per poter trattare questo tipo di problemi con i metodi diretti del calcolo delle variazioni, è opportuno modificare il quadro funzionale e ambientare il problema nello spazio BV (Ω) delle funzioni con variazione limitata su Ω, costituito dalle funzioni u in L¹ (Ω) le cui derivate parziali deboli, invece di essere delle funzioni, sono delle misure con variazione limitata su Ω. Su tale spazio è possibile calcolare il funzionale rilassato Å mediante una formula che utilizza integrali rispetto a opportune misure singolari. Nel caso che f (x, y, η) sia convessa in η si ha Å (u) = F (u) per ogni funzione u in W^{1, 1} (Ω). Questo mostra che il funzionale rilassato costituisce in questo caso un'estensione del funzionale originario.

Nel caso di problemi con condizioni al contorno del tipo u (x) = ϕ (x) su ∂Ω si ottiene un problema rilassato che include anche un termine di penalizzazione su ∂Ω del tipo visto per il funzionale dell'area. Poiché la (8) fornisce la coercitività di F in BV (Ω) rispetto alla convergenza L¹ (Ω), i metodi diretti del calcolo delle variazioni permettono di risolvere questi problemi di minimo rilassati nello spazio BV (Ω). In molti casi interessanti le soluzioni deboli così ottenute sono più regolari e forniscono dunque una soluzione del problema di minimo per F.

d) Convergenze variazionali e applicazioni.

Un procedimento analogo al rilassamento può essere usato per definire una nozione di convergenza di tipo variazionale sull'insieme dei funzionali definiti su un dato spazio U. La nozione generale di Γ-convergenza è stata introdotta da De Giorgi e T. Franzoni nel 1975 per spazi topologici generali. Nel caso in cui U sia uno spazio metrico, come ad esempio gli spazi L^p considerati nei capitoli precedenti, essa può essere espressa nel modo seguente: sia F_n una successione di funzionali definiti su U e a valori nella retta reale estesa −R, che si ottiene aggiungendo alla retta reale R i due punti + ∞ e - ∞. Si dice che F_n ‛Γ-converge' a un funzionale F, anch'esso definito su U, se sono verificate le seguenti condizioni: 1) per ogni u in U e ogni successione u_n convergente a u in U, per cui esista (finito o infinito) il limite

F_n (u_n), si ha F (u) ≤

F_n (u_n); 2) per ogni u in U esiste una successione v_n convergente a u in U tale che F (u) =

F_n (v_n). La Γ-convergenza si è dimostrata finora uno strumento utilissimo nello studio dell'approssimazione variazionale di funzionali integrali. Essa verifica le seguenti proprietà, analoghe a quelle viste precedentemente per il rilassamento: se un funzionale F è il Γ-limite di una successione F_n, allora F è semicontinuo inferiormente; inoltre, se i funzionali F_n sono uniformemente coercitivi (cioè esiste un funzionale coercitivo Ψ, indipendente da n, tale che F_n (u) ≥ Ψ (u) per ogni u), allora il funzionale F risulta anch'esso coercitivo, e dunque ammette un punto di minimo.

Diremo che u_n è una successione ‛asintoticamente minimizzante' per F_n se esistono delle costanti c_n tali che c_n ≤ F_n (v) per ogni v in U e la differenza F_n (u_n) - c_n tende a zero per n → ∞. In particolare, se u_n è un punto di minimo per F_n per ogni n, allora u_n è una successione asintoticamente minimizzante, potendosi prendere c_n = F_n (u_n). Se F_n è una successione di funzionali uniformemente coercitivi che Γ-converge a F, allora valgono le seguenti proprietà che collegano i punti di minimo di F alle successioni asintoticamente minimizzanti per F_n: 1) se u è un punto di minimo per F, allora esiste una successione u_n asintoticamente minimizzante per F_n che converge a u; 2) se v_n è una successione asintoticamente minimizzante per F_n che converge a un elemento v di U, allora v è un punto di minimo per F e F_n (v_n) tende a F (v) per n → ∞.

In particolare, se F ha un unico punto di minimo u, e u_n è un punto di minimo per F_n per ogni n, allora u_n converge a u per n → ∞.

Esempi particolarmente significativi di successioni di funzionali Γ-convergenti si ritrovano nei problemi di omogeneizzazione, che hanno molte applicazioni in ingegne-ria, come la modellizzazione e lo studio dei materiali compositi. Uno dei problemi più tipici nella teoria dell'omogeneizzazione è il seguente: data una funzione a (x) = a (x₁, ..., x_n), definita nello spazio euclideo n-dimensionale e periodica di periodo uno rispetto a ciascuna delle variabili x₁, ..., x_n, si tratta di studiare il comportamento asintotico, quando ε tende a zero, delle soluzioni u_ε dei problemi di Dirichlet

dove Ω è un dominio limitato e regolare dello spazio euclideo n-dimensionale, f e ϕ sono funzioni sufficientemente regolari definite rispettivamente su Ω e su ∂Ω, e L_ε è l'operatore definito da

Il problema (9) può essere usato per descrivere il flusso di corrente elettrica attraverso un conduttore a struttura periodica, di periodo ε, la cui conduttività è determinata, punto per punto, dalla funzione scalare a

Il materiale di cui è costituito il conduttore è dunque isotropo, perché la conduttività non dipende dalla direzione in cui fluisce la corrente, e non omogeneo, perché la conduttività varia da punto a punto.

Lo stesso problema (9) può servire da modello di parecchi altri funzionamenti fisici di tipo lineare, caratterizzati cioè dal principio di sovrapposizione degli effetti, che si verificano in un mezzo isotropo non omogeneo a struttura periodica, le cui proprietà sono determinate in ciascun punto dalla funzione scalare a

, mentre f rappresenta le influenze esterne e ϕ le condizioni al contorno. Il problema matematico dello studio del limite delle soluzioni di (9) per ε tendente a zero traduce quindi la descrizione del comportamento asintotico del mezzo periodico, quando il periodo tende a zero.

Supponiamo che esistano due costanti c₁ e c₂ tali che 0 〈 c₁ ≤ a (x) ≤ c₂. Essendo (9) l'equazione di Eulero del funzionale

lo studio del comportamento asintotico di u_ε si può ricondurre allo studio del Γ-limite, per ε → 0, della successione F_ε, quando si prenda come spazio U di funzioni ammissibili lo spazio di Sobolev delle funzioni di W^{1, 2} (Ω) con traccia uguale a ϕ su ∂Ω, munito della convergenza L² (Ω). Si dimostra che F_ε Γ-converge, per ε → 0, a un funzionale F₀ della forma

con opportuni coefficienti costanti α_ij, che dipendono dalla funzione a, ma non da f e da ϕ, e che è possibile determinare risolvendo dei problemi di minimo ausiliari sulla cella di periodicità.

L'equazione di Eulero associata al funzionale F₀ è

dove L₀u (x) è l'operatore definito da

In base alle proprietà dei Γ-limiti ricordate sopra, si ha che u_ε (punto di minimo di F_ε) converge in L² (Ω) a u₀ (punto di minimo di F₀). Il problema (10) descrive il comportamento di un mezzo omogeneo, le cui proprietà fisiche sono determinate dalla matrice α_ij. Il comportamento del mezzo non omogeneo descritto dal problema (9) risulta quindi bene approssimato, quando ε è molto piccolo, da quello del mezzo omogeneo descritto dal problema (10), da cui il nome di omogeneizzazione con il quale ci si riferisce a questo tipo di problemi. Poiché la matrice α_ij non è, di solito, un multiplo della matrice identica, il mezzo descritto dal problema (10) è, in generale, anisotropo, cioè presenta un comportamento diverso nelle varie direzioni. È da notare che col processo di omogeneizzazione si può ottenere un mezzo anisotropo come limite di mezzi isotropi non omogenei. La dimostrazione che ogni mezzo anisotropo è ottenibile come limite di mezzi isotropi è stata data da A. Marino e S. Spagnolo nel 1969.

8. Problemi geometrici

Uno dei più interessanti problemi geometrici del calcolo delle variazioni è il problema delle superfici di area minima, detto anche problema di Plateau in onore del fisico belga che nel suo trattato del 1873 descrisse un gran numero di esperimenti su pellicole liquide sottili. J. Plateau notò che ogni contorno costituito da un filo chiuso, di qualunque forma geometrica, delimita sempre almeno una pellicola di liquido in equilibrio stabile. La teoria fenomenologica della capillarità attribuisce a ogni pellicola di acqua saponata un'energia potenziale proporzionale alla sua area. In base al principio dei lavori virtuali, le pellicole in equilibrio stabile corrispondono dunque a superfici di area minima tra quelle aventi lo stesso contorno.

a) Superfici minime parametriche.

Per formulare il problema di Plateau in forma rigorosa bisogna precisare la nozione di superficie. Un modo consiste nel descrivere le superfici in forma parametrica x = x (u, v), y = y (u, v), z = z (u, v), chiedendo che il punto di coordinate (u, v) vari, ad esempio, nel cerchio unitario. Si parla, in questo caso, di superfici del tipo del disco. Limitandosi a cercare il minimo in questa classe, il problema di Plateau si formula nel modo seguente: assegnata una curva semplice chiusa Γ nello spazio euclideo tridimensionale, trovare le superfici del tipo del disco aventi area minima tra tutte quelle aventi Γ per contorno. Nel secolo scorso il problema di Plateau fu risolto per molte curve speciali. L'esistenza di una soluzione parametrica del tipo del disco nel caso di un'arbitraria curva semplice chiusa Γ di lunghezza finita fu dimostrata nel 1930 da J. Douglas e, indipendentemente, da T. Radó. Una notevole semplificazione della dimostrazione fu trovata nel 1936 da R. Courant e, indipendentemente, da L. Tonelli. Un risultato di esistenza del tutto analogo vale quando Γ sia una curva semplice chiusa di lunghezza finita nello spazio euclideo n-dimensionale e si cerchi in tale spazio una superficie bidimensionale del tipo del disco di area minima tra quelle aventi Γ per contorno.

b) Frontiere di area minima.

Nello spazio euclideo n-dimensionale Rⁿ, i metodi utilizzati per ottenere i risultati esposti nel paragrafo precedente non si estendono al caso di varietà di dimensione k con 2 〈 k 〈 nO. Nel caso di codimensione uno, cioè k = n - 1, è possibile formulare e risolvere interessanti problemi del tipo del problema di Plateau mediante la teoria dei perimetri introdotta da R. Caccioppoli e De Giorgi negli anni cinquanta. Data una regione Ω dello spazio euclideo Rⁿ e un arbitrario sottoinsieme E di tale spazio, il perimetro di E in Ω, che si indica con P (E, Ω), è definito come la più piccola costante c per cui valga la diseguaglianza

per ogni famiglia (ϕ₁, ..., ϕ_n) di n funzioni definite su Rⁿ, nulle fuori di una regione limitata contenuta in Ω e avente distanza positiva dal bordo di Ω, dotate di derivate parziali continue in tutto Rⁿ, e tali che sia sempre Σ_i [ϕ_i (x)]² ≤ 1. Se non esiste alcuna costante c con queste proprietà si pone P (E, Ω) = + ∞. Nel caso n = 2, utilizzando le formule di Gauss-Green si verifica facilmente che, se E è un poligono e Ω è l'intero piano, allora P (E, Ω) coincide con il perimetro di E inteso nel senso della geometria elementare; più in generale, se E è un insieme con il bordo ∂E sufficientemente regolare e Ω è un dominio del piano, allora P (E, Ω) è uguale alla lunghezza della porzione del bordo di E interna a Ω. Tornando al caso n-dimensionale, se il bordo di E è sufficientemente regolare, allora P (E, Ω) coincide con la misura (n - 1)-dimensionale della parte del bordo di E interna a Ω. A ogni modo, qualunque sia l'insieme E, è possibile attribuire al perimetro di E in Ω un ben determinato valore, finito o infinito. Nel caso in cui Ω = Rⁿ si usa la notazione P (E) e si parla semplicemente di perimetro di E.

Nel linguaggio della teoria dei perimetri, diremo che un insieme E ha frontiera minima in un dominio limitato Ω se P (E, Ω) 〈 + ∞ e P (E, Ω) ≤ P (F, Ω) per ogni altro insieme F che coincida con E vicino al bordo di Ω. La questione cruciale in questo approccio, in cui, almeno inizialmente, si considerano anche insiemi E molto irregolari, per i quali P (E, Ω) sostituisce la nozione di area del bordo di E, consiste nel dimostrare la regolarità degli insiemi con frontiera localmente minima. Per n ≤ 7 i risultati ottenuti da De Giorgi negli anni sessanta permettono di stabilire che, se E ha frontiera minima in Ω, allora la parte del bordo di E che è interna a Ω è una varietà (n - 1)-dimensionale regolare. Nel caso n = 8 il cono di Simons, costituito dai punti le cui coordinate (x₁, ..., x₈) soddisfano la diseguaglianza

x²₁ + x²₂ + x²₃ + x²₄ > x²₅ + x²₆ + x²₇ + x²₈,

è un esempio di insieme E la cui frontiera, pur non essendo regolare nel punto di coordinate (0, ..., 0), è minima in ogni dominio limitato Ω contenuto in R⁸ (Bombieri, De Giorgi e Giusti, 1969). Nel caso n ≥ 8, H. Federer ha dimostrato nel 1970 che, se E ha frontiera minima in Ω, allora la parte del bordo di E che è contenuta in Ω è una varietà (n - 1)-dimensionale regolare, eccettuato un insieme singolare di dimensione minore o uguale a n - 8.

Con questi stessi metodi si possono ottenere risultati analoghi di esistenza e di regolarità per altri problemi di natura geometrica, quali, ad esempio, i problemi di area minima a volume assegnato: dato un dominio limitato Ω dello spazio euclideo n-dimensionale e fissata una costante c minore del volume n-dimensionale di Ω, si tratta di trovare i sottoinsiemi E di Ω che rendono minimo il perimetro P (E, Ω) nella classe di tutti i sottoinsiemi di Ω di volume c. Nel quadro della teoria dei perimetri è possibile dimostrare la proprietà isoperimetrica della sfera in condizioni di estrema generalità. Precisamente De Giorgi (1958) ha provato che tra tutti gli insiemi di misura n-dimensionale assegnata in Rⁿ, la sfera ha perimetro minimo.

c) Varietà minime di dimensione arbitraria.

Nello spazio euclideo n-dimensionale, l'analogo del problema di Plateau per varietà di dimensione k è il seguente problema: assegnata una varietà regolare orientata Γ di dimensione k - 1 che sia limitata e priva di bordo, trovare una varietà orientata S di dimensione k di misura k-dimensionale minima tra tutte quelle aventi Γ come bordo orientato. Secondo un uso ormai consolidato nel moderno calcolo delle variazioni, anche questo problema è stato risolto utilizzando per prima cosa una formulazione debole, in cui si allarga la classe ove si cerca il minimo, includendovi oggetti anche molto irregolari. In questo caso la formulazione debole del problema è espressa nel linguaggio della teoria delle correnti rettificabili, che possono essere considerate come una generalizzazione della nozione di varietà k-dimensionale orientata; tale teoria include diversi nuovi enti che possono essere identificati con varietà anche molto irregolari, ma per i quali si può comunque parlare, in un senso tecnico ben preciso, di bordo orientato e di misura k-dimensionale. L'esistenza di una soluzione nello spazio delle correnti rettificabili si ottiene con i metodi diretti grazie al teorema di compattezza di H. Federer e W. H. Fleming (1960). Per quanto riguarda la regolarità delle soluzioni vi sono dei risultati parziali per 1 〈 k 〈 n - 1 e risultati completi nel caso k = n - 1, che utilizzano le tecniche sviluppate nella teoria dei perimetri: se n ≤ 7, allora le correnti minime di dimensione n - 1 sono varietà regolari al di fuori di Γ, mentre, se n ≥ 8, esse possono presentare un insieme singolare di dimensione minore o uguale a n - 8 (v. Federer, 1969).

d) Problemi con discontinuità libera.

Di recente è stato possibile affrontare una nuova classe di problemi, detti problemi con discontinuità libera, in cui il funzionale da minimizzare dipende da una funzione u che risulta discontinua su una superficie S a priori incognita. In generale questo funzionale contiene un integrale di volume, sul complementare di S, dipendente dalla funzione u e dalle sue derivate, e un termine dipendente dalla superficie S di discontinuità. Questi problemi mescolano dunque le caratteristiche dei problemi di minimo per funzionali integrali con quelle dei problemi di tipo geometrico.

Il prototipo dei problemi con discontinuità libera fu proposto nel 1985 da D. Mumford e J. Shah e, nel caso n = 2, esso è collegato a problemi di segmentazione d'immagine nella teoria della visione artificiale. Data una regione limitata Ω dello spazio euclideo n-dimensionale e una funzione limitata g definita su Ω, il problema consiste nel trovare il minimo del funzionale

dove Ω S indica l'insieme dei punti di Ω che non stanno in S e ???03???^n-1 (S) indica la misura (n - 1)-dimensionale di S. La principale novità di questo problema consiste nel fatto che vi sono due variabili rispetto a cui va cercato il minimo: una è l'insieme S, che varia tra i sottoinsiemi di Ω di misura (n - 1)-dimensionale finita, e l'altra è la funzione u, che varia tra le funzioni continue e dotate di derivate parziali continue su Ω S. Questo problema è stato risolto dimostrando con i metodi diretti l'esistenza di un'opportuna soluzione generalizzata nel nuovo spazio funzionale SBV (Ω) delle funzioni a variazione limitata di tipo speciale, introdotto da L. Ambrosio e De Giorgi nel 1988, e dimostrando poi che la soluzione generalizzata così trovata fornisce una soluzione del problema proposto (M. Carriero, E. De Giorgi e A. Leaci, 1989). Successivamente è stato dimostrato che per un punto di minimo (u, S) l'insieme S è una varietà regolare di dimensione n - 1, a meno di un insieme singolare avente misura (n - 1)-dimensionale nulla (L. Ambrosio, N. Fusco e D. Pallara, 1995). La regolarità della funzione u segue a questo punto dai risultati classici di regolarità per i minimi dell'integrale di Dirichlet. Rimangono aperti problemi interessanti a proposito della struttura dell'insieme singolare della varietà S. In particolare, è ancora aperto il problema di stabilire se per n = 2 questo insieme singolare sia costituito da un numero finito di punti.

Funzionali del tipo di quello considerato da Mumford e Shah, oltre che in teoria della visione, si incontrano anche in varie questioni di fisica matematica, per esempio nello studio delle fratture.

BIBLIOGRAFIA

Bolza, O., Vorlesungen über Variationsrechnung, Leipzig 1909.

Buttazzo, G., Semicontinuity, relaxation and integral representation in the calculus of variations, Harlow 1989.

Carathéodory, C., Variationsrechnung und partielle Differentialgleichungen erster Ordnung, Leipzig 1935.

Cesari, L., Optimization-theory and applications: problems with ordinary differential equations, New York 1983.

Courant, R., Dirichlet's principle, conformal mapping, and minimal surfaces, New York 1950.

Dacorogna, B., Direct methods in the calculus of variations, Berlin-New York 1989.

Dal Maso, G., An introduction to Γ-convergence, Boston 1993.

De Giorgi, E., Colombini, F., Piccinini, L. C., Frontiere orientate di misura minima e questioni collegate, Pisa 1972.

Dierkes, U., Hildebrandt, S., Küster, A., Wohlrab, O., Minimal surfaces, 2 voll., Berlin-New York 1992.

Ekeland, I., Temam, R., Analyse convexe et problèmes variationnels, Paris 1974.

Federer, H., Geometric measure theory, Berlin-Heidelberg-New York 1969.

Giaquinta, M., Hildebrandt, S., Calculus of variations, 2 voll., Berlin-New York 1996.

Giusti, E., Metodi diretti nel calcolo delle variazioni, Bologna 1994.

Goldstine, H. H., A history of the calculus of variations from the 17th through the 19th century, Berlin 1980.

Hildebrandt, S., Tromba, A., Mathematics and optimal form, New York 1985.

Kinderlehrer, D., Stampacchia, G., An introduction to variational inequalities and their applications, New York 1980.

Massari, U., Miranda, M., Minimal surfaces of codimension one, Amsterdam-New York 1984.

Morrey, C. B., Multiple integrals in the calculus of variations, Berlin 1966.

Nitsche, J. C., Vorlesungen über Minimalflächen, Berlin 1975.

Radó, T., On the problem of Plateau, Berlin 1933.

Tikhomirov, V. M., Rasskazy o maksimumakh i minimumakh, Moskva 1986 (tr. ingl.: Stories about maxima and minima, Providence, R. I., 1990).

Tonelli, L., Fondamenti di calcolo delle variazioni, Bologna 1921.

Young, L. C., Lectures on the calculus of variations and optimal control theory, Philadelphia, Pa., 1969.