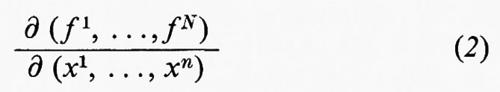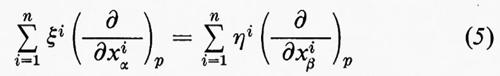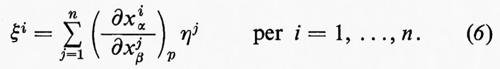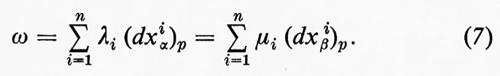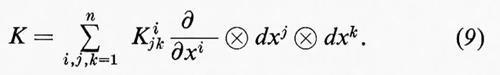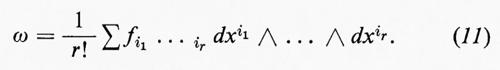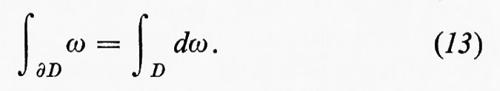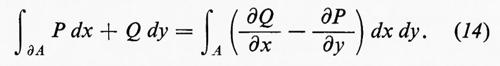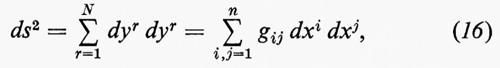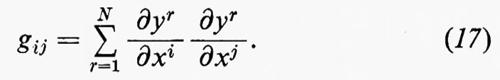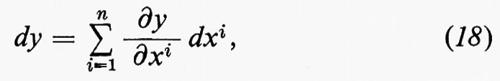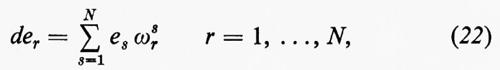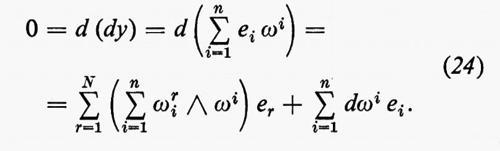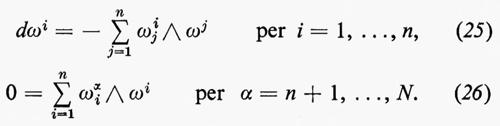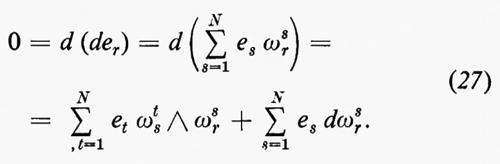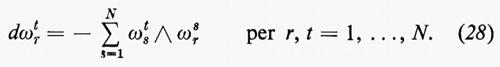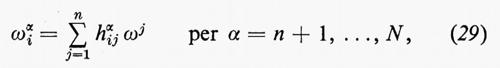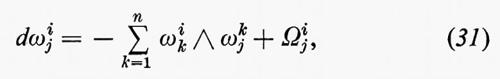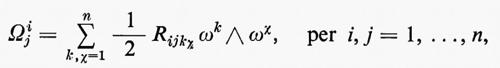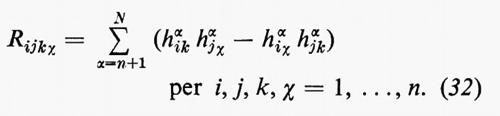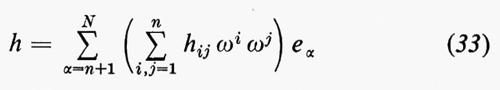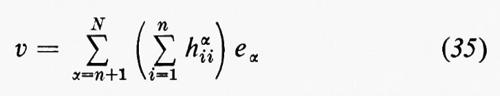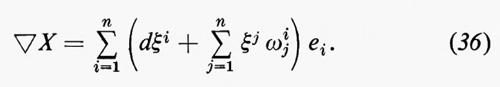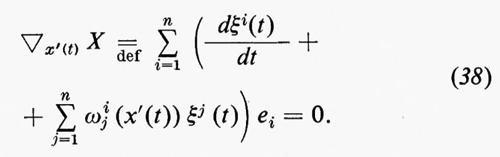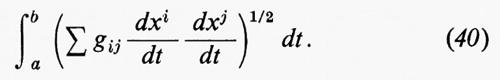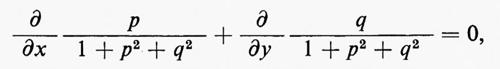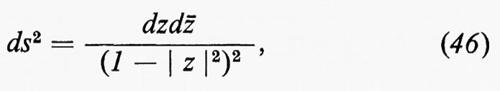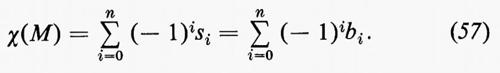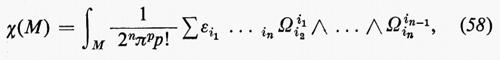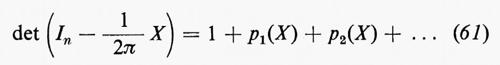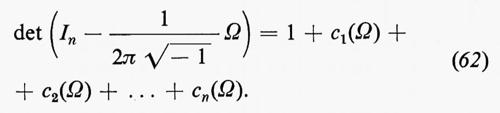Geometria differenziale

Geometria differenziale

di Shoshichi Kobayashi

Geometria differenziale

sommario: 1. Cenno storico. 2. Varietà. 3. Geometria riemanniana. 4. Varietà complesse e varietà kähleriane. 5. Classi caratteristiche. 6. Sviluppi della geometria differenziale. □ Bibliografia.

1. Cenno storico

La geometria differenziale, un ramo della matematica in cui il calcolo differenziale e integrale è applicato allo studio degli oggetti geometrici, è antica quanto il calcolo stesso. Tuttavia non vi fu una sistemazione organica della geometria differenziale delle superfici fino al 1827, anno in cui C. F. Gauss pubblicò le sue Disquisitiones circa superficies curvas. Gauss riconobbe l'importanza della geometria intrinseca delle superfici, e generalmente si conviene che la geometria differenziale, così come è nota al giorno d'oggi, abbia avuto in Gauss il suo iniziatore.

Gauss fu seguito da G. F. B. Riemann. Già nella sua prolusione inaugurale a Göttingen, Riemann affermava che la geometria differenziale intrinseca è completamente indipendente dall'immersione (Über die Hypothesen, welche der Geometrie zugrunde liegen). Tolta la restrizione di limitarsi a considerare il caso 2-dimensionale e considerate varietà astratte di dimensione n, Riemann introdusse quella che oggi è nota come metrica riemanniana; in effetti egli considerò metriche più generali che formarono l'oggetto della dissertazione di P. Finsler nel 1918.

La famosa prolusione inaugurale di F. Klein a Erlangen nel 1872, nota come il ‛Programma di Erlangen', esercitò una vasta influenza sullo sviluppo della geometria alla fine del secolo scorso e agli inizi di questo. Klein definì la geometria come lo studio di quelle proprietà delle figure che rimangono invariate rispetto a un particolare gruppo di trasformazioni, per esempio il gruppo delle trasformazioni proiettive e i suoi sottogruppi, quali il gruppo delle trasformazioni affini o il gruppo dei movimenti rigidi. Così, la geometria euclidea è lo studio degli invarianti per il gruppo dei movimenti rigidi. Dato che la maggior parte delle varietà riemanniane ammette un piccolo numero di isometrie, in un primo tempo la geometria riemanniana sembrò non rispettare la definizione di geometria data da Klein. Questa discordanza rimase insoluta per mezzo secolo.

Nel frattempo vi furono tre sviluppi principali nella geometria differenziale. Nel loro lavoro pubblicato nei ‟Matematische Annalen", G. Ricci-Curbastro e T. Levi-Civita (v., 1900) svilupparono il calcolo tensoriale come un potente strumento per la geometria riemanniana. Il calcolo tensoriale risultò essere precisamente ciò di cui A. Finstein aveva bisogno per descrivere la sua teoria della relatività generale (Die Grundlagen der allgemeinen Relativitätstheorie, 1916). Questo fatto suscitò l'interesse nei confronti della geometria riemanniana. Nel 1917 Levi-Civita introdusse la nozione di parallelismo nella geometria riemanniana e ciò attribuì significato geometrico al calcolo tensoriale formale di Ricci-Curbastro e Levi-Civita.

Nel 1918, H. Weyl sviluppò la geometria differenziale affine basata esclusivamente sulla nozione di parallelismo e non sulla metrica riemanniana. Assumendo il punto di vista della teoria degli invarianti, egli creò nel 1921 la teoria delle connessioni proiettive e conformi. Il suo punto di vista, adottato da L. P. Eisenhart, O. Veblen e T. Y. Thomas, dominò la geometria differenziale in America negli anni venti e trenta.

In una serie di lavori pubblicati tra il 1923 e il 1925, E. Cartan sviluppò anche la teoria delle connessioni affini, proiettive e conformi secondo il punto di vista di Klein. Così come ogni spazio tangente di una varietà riemanniana è considerato come uno spazio euclideo, una connessione affine considera lo spazio tangente in ogni punto come uno spazio affine e lo sviluppa sopra lo spazio tangente in un punto infinitamente prossimo. Nel discutere le connessioni proiettive, Cartan associò uno spazio proiettivo a ogni punto come un'approssimazione infinitesima. Analogamente per le connessioni conformi. Così, nell'infinitesimo, il Programma di Erlangen è ancora valido.

Il metodo del riferimento mobile, creato da G. Darboux e ampiamente sviluppato da Cartan nella sua teoria delle connessioni, fu un precursore della teoria degli spazi fibrati. Combinando l'algebra di Grassman con il calcolo differenziale, Cartan inventò un potente strumento di calcolo noto come calcolo delle forme differenziali. Da allora esso è diventato indispensabile in topologia, in geometria algebrica e nella teoria delle funzioni di più variabili complesse, così come in geometria differenziale.

Il lavoro del matematico norvegese S. Lie, compagno di studi di Klein a Göttingen, sui gruppi di trasformazioni ebbe anche una profonda influenza su Cartan. Il lavoro di quest'ultimo sui gruppi di Lie, in particolare sui gruppi di Lie semplici, e sulla geometria differenziale culminò nel 1926 nella sua scoperta degli spazi riemanniani simmetrici. Questi spazi offrono una naturale generalizzazione della superficie sferica nello spazio euclideo e del disco unitario nel piano complesso con la metrica di Poincaré. Essi sono diventati sempre più importanti, dato il ruolo essenziale che giocano nella teoria delle rappresentazioni unitarie e in altri campi della matematica.

Eccettuati i lavori di Cartan, la geometria differenziale negli anni venti si occupava soprattutto di superfici nello spazio euclideo 3-dimensionale e di proprietà locali di varietà riemanniane. Ma l'orientamento verso la geometria differenziale globale (cioè la geometria differenziale che riguarda le proprietà delle varietà nel loro complesso) cominciò lentamente all'inizio degli anni trenta con la dissertazione di G. de Rham pubblicata nel 1931. Il teorema di de Rham stabilisce che lo spazio delle forme differenziali chiuse di grado r a meno dello spazio delle forme esatte di ugual grado è isomorfo all'r-mo gruppo di coomologia reale. L'importanza di questo teorema è dovuta al fatto che esso fornisce il fondamento teorico per esprimere invarianti coomologici di una varietà mediante invarianti geometrici differenziali. In una serie di lavori immediatamente successivi alla tesi di de Rham, W. V. D. Hodge stabilì che, su una varietà riemanniana compatta, ogni classe di coomologia r-dimensionale può essere univocamente rappresentata da una forma armonica di grado r.

Un'importante classe di varietà complesse con metrica riemanniana compatibile fu scoperta da J. A. Schouten e D. van Dantzig nel 1929 e da E. Kähler nel 1932. Questa classe di varietà, chiamate oggi varietà kähleriane, comprende le varietà algebriche. La teoria di Hodge degli integrali armonici è più efficace quando è applicata a varietà kähleriane compatte.

Il teorema globale più famoso nella geometria differenziale classica delle superfici è la formula di Gauss-Bonnet (1848). Applicata a una superficie orientabile chiusa, essa afferma che l'integrale della curvatura gaussiana è uguale a 2π volte il numero di Eulero della superficie. La formula fu generalizzata a ipersuperfici chiuse nello spazio euclideo di dimensione arbitraria da H. Hopf, nel 1925, a sottovarietà chiuse di spazi euclidei da C. B. Allendoerfer e anche da W. Fenchel, nel 1940, e infine a varietà riemanniane chiuse arbitrarie da Allendoerfer e A. Weil, nel 1943. Ma la semplice dimostrazione data da S. S. Chern nel 1944 conteneva la nozione di trasgressione che è diventata essenziale nella teoria delle classi caratteristiche. Questo risultò essere, per dir così, la punta di un iceberg. La scoperta delle classi di Pontrjagin per le varietà riemanniane (1944) e delle classi di Chern per le varietà hermitiane (1946) culminò nel teorema dell'indice e nel teorema di Riemann-Roch di Hirzebruch e infine nel teorema dell'indice di Atiyah e Singer.

Una semplice ma fruttuosa idea di S. Bochner, che metteva in relazione le forme armoniche con la curvatura, stabilì dei ‛teoremi di annullamento' per forme armoniche di varietà riemanniane e per forme olomorfe di varietà kähleriane, sotto opportune condizioni di positività per la curvatura (1946-1947). Tale idea ha portato al teorema di annullamento di Kodaira e ad altri teoremi di annullamento.

Lo studio delle geodetiche è uno degli argomenti più antichi in geometria differenziale. Dato che le geodetiche appaiono come punti critici di certi funzionali, il calcolo delle variazioni, che risale a L. Euler e J. L. Lagrange, è uno strumento naturale di ricerca. L'esistenza di geodetiche chiuse, in relazione a problemi dinamici, è stata una delle questioni centrali della geometria differenziale fin dal tempo di H. Poincaré, il quale dimostrò l'esistenza di una geodetica chiusa su ogni superficie convessa (1905). Questo risultato fu esteso da G. D. Birkhoff a dimensioni più elevate. Il calcolo delle variazioni in grande, iniziato da Poincaré e Birkhoff, fu sistematicamente sviluppato nella forma moderna da M. Morse. Lavori recenti sulle geodetiche chiuse si basano in modo essenziale sulla teoria di Morse o su sue varianti. Inoltre studi profondi sulle geodetiche condussero H. Rauch, W. Klingenberg, M. Berger e altri a una migliore comprensione delle varietà riemanniane a curvatura positiva.

La teoria delle superfici minime ebbe inizio con Lagrange come un'ulteriore applicazione del suo calcolo delle variazioni. Al primo stadio di sviluppo, G. Monge, J. B. M. C. Meusnier, A. M. Legendre, O. Bonnet, B. Riemann, K. Weierstrass, H. A. Schwarz, E. Beltrami e S. Lie contribuirono alla teoria. Weierstrass e Schwarz stabilirono le sue relazioni con la teoria delle funzioni. Le superfici minime sono le superfici di minima area spazzate da una data curva chiusa dello spazio. J. A. Plateau dimostrò sperimentalmente che le superfici minime possono essere realizzate con pellicole di sapone intingendo un filo di ferro, modellato come una curva chiusa sghemba, in una soluzione di sapone (1873). Il problema di Plateau è di dimostrare matematicamente l'esistenza di superfici minime con una assegnata curva al contorno. Il problema fu risolto per curve di Jordan da T. Radò nel 1930 e, indipendentemente, da J. Douglas nel 1931. I due problemi sulle superfici minime che attrassero di più l'attenzione sono il problema di Plateau e il problema di Bernstein. Quest'ultimo è un problema su ipersuperfici minime negli spazi euclidei di dimensione più alta. Sia y=f(x¹, ..., xⁿ) definita per tutti i valori di (x¹, ..., xⁿ) nello spazio euclideo n-dimensionale e supponiamo che il suo grafico sia una sottovarietà minima dello spazio euclideo (n+1)-dimensionale. S. N. Berňstejn mostrò che il grafico è necessariamente un piano per n=2 (1927). Il problema di estendere il risultato di Berňstejn a dimensioni più alte ebbe un esito sorprendente: la generalizzazione per n=3, data da E. de Giorgi (1965), per n=4, data da F. J. Almgren (1966), e per n=5, 6, 7, data da J. Simons (1968), fu seguita dalla scoperta di controesempi per n≥8 fatta da E. Bombieri, E. de Giorgi ed E. Giusti (1969). In anni recenti numerosi risultati sono stati ottenuti non solo per superftci minime negli spazi euclidei 3-dimensionali, ma anche per sottovarietà minime in spazi euclidei a dimensione più elevata, in sfere e in altri spazi simmetrici. Quantunque il legame con la teoria delle funzioni si perda per sottovarietà minime di dimensione più alta, esso si mantiene tuttavia per superfici minime di spazi euclidei di dimensione maggiore di 3; infatti, Chern e R. Osserman hanno applicato con successo la generalizzazione della teoria di Nevanlinna, data da Ahlfors e Weyl, all'applicazione di Gauss generalizzata.

2. Varietà

Una varietà è l'analogo a più dimensioni di una superficie. Per esempio, se

y¹=f¹ (x¹, ..., xⁿ), ..., y^N=f^N (x¹, ..., xⁿ), N>n, (1)

è un sistema di funzioni definito in un dominio D nello spazio euclideo n-dimensionale Rⁿ, tale che la matrice jacobiana

sia di rango massimo n, allora, mentre (x¹, ..., xⁿ) spazza il dominio D, (y¹, ..., y^N) descrive una superficie n-dimensionale, cioè una varietà n-dimensionale giacente nello spazio euclideo N-dimensionale R^N. Per descrivere una varietà generale in R^N, non è sufficiente avere un singolo sistema di funzioni (1). Una varietà n-dimensionale M in R^N è ricoperta (con sovrapposizioni) da un insieme numerabile di porzioni di varietà U_α ciascuna delle quali è definita da un sistema di funzioni

y¹=f¹_α (x¹, ..., xⁿ), ..., y^N=fN_α (x¹, ..., xⁿ) (3)

definito in un dominio D_α di Rⁿ con la matrice jacobiana di rango n. Per semplicità, supponiamo che due punti distinti di D_α corrispondano a punti distinti di U_α. Così una varietà M è ricoperta da sottoinsiemi U_α, detti intorni coordinati, ciascuno dei quali è in corrispondenza biunivoca con un dominio D_α di Rⁿ. Mediante questa corrispondenza noi abbiamo funzioni coordinate (x¹_α, ..., xn_α) su U_α che corrispondono a (x¹, ..., xⁿ) in D_α. Quantunque una varietà generale M possa essere definita astrattamente mediante intorni coordinati e funzioni coordinate, senza riferimento allo spazio euclideo ambiente R^N, tuttavia può sempre essere realizzata (cioè immersa) come una varietà in R^N per N sufficientemente grande (di fatto, per N=2n); questo è noto come il teorema di immersione di Whitney (1944). Dato che alcuni punti di M sono contenuti in più di un intorno coordinato, solo quelle entità e quantità che sono invarianti o obbediscono a certe regole ben definite per un cambiamento di coordinate sono significative geometricamente. Un vettore tangente di una varietà M è una siffatta entità. Quando M giace in R^N, il suo significato geometrico è chiaro. Astrattamente può essere definito come una derivata direzionale. Così un vettore tangente X a un punto p di M si può esprimere nella forma

se p è in U_α. I coefficienti ξ¹, ..., ξⁿ si chiamano le componenti di X rispetto alle coordinate x¹_α, ..., xn_α. Se p è anche in U_β e se η¹, ..., ηⁿ sono le componenti dello stesso vettore X rispetto a X¹_β, ..., Xn_β, allora l'uguaglianza

implica la legge di trasformazione:

I vettori tangenti a p formano lo spazio tangente a p:T_p=T_p(M). Un elemento del suo spazio duale T^*_p=T^*_p(M) può esprimersi nella forma

In accordo con la (7), le sue componenti obbediscono alla legge di trasformazione:

Un elemento di T^*_p è chiamato un covettore o un vettore covariante, mentre un vettore tangente è talvolta chiamato un vettore contravariante.

Da T_p(M) e T^*_p(M) si può generare l'algebra tensoriale. Per esempio, un elemento di T_p⊗T^*_p⊗T^*_p, detto tensore di grado contravariante 1 e grado covariante 2 o tensore di tipo (1, 2), si può esprimere nella forma

(Come nella (9) ometteremo per semplicità gli indici p ed α, a meno che essi non siano assolutamente necessari). Le componenti Ki_jk obbediscono alla legge di trasformazione prescritta dalla (6) e dalla (8). Quando si assegna un vettore o, più in generale, un tensore a ciascun punto di M, si ottiene un campo vettoriale o un campo tensoriale. Un campo di vettori covarianti si chiama anche una 1-forma (differenziale) o una forma pfaffiana in onore di J. F. Pfaff.

Per introdurre forme differenziali di grado più alto, de- finiamo una moltiplicazione di differenziali soggetta alla seguente regola antisimmetrica:

dxⁱ⋀dx^j=−dx^j⋀dxⁱ, cosicché dxⁱ⋀dxⁱ=0. (10)

Una r-forma ω si può allora scrivere nella forma:

L'imporre la condizione che i coefficienti f_i1..._ir siano antisimmetrici rende l'espressione (11) univoca e fa sì che sia possibile identificare la forma ω con il campo tensoriale covariante antisimmetrico di componenti f_i1..._ir. La derivata esterna di ω è la (r+1)-forma

Formula

Una r-forma si dice chiusa se dω=0, esatta se ω=dϑ per qualche (r−1)-forma ϑ. Dalla (12) segue che d(dω)=0, cioè ogni forma esatta è necessariamente chiusa. Lo spazio quoziente delle r-forme chiuse modulo il sottospazio delle r-forme esatte è il gruppo di coomologia di de Rham di M in dimensione r e si indica con Hr_R(M). Se D è un dominio (r+1)-dimensionale con frontiera ∂D e ω è una r-forma, allora

La (13) è nota come formula di Stokes e contiene come caso particolare il teorema di Green:

Grazie alla linearità dell'integrale la formula di Stokes continua a valere anche quando D è una catena (r+1)-dimensionale e ne segue perciò che ogni elemento di Hr_R(M) può essere integrato senza ambiguità su una qualunque classe di omologia r-dimensionale; il teorema fondamentale di de Rham stabilisce che Hr_R(M) è isomorfo, in questo modo naturale, al gruppo di coomologia reale di M.

Scegliendo una base, per esempio del tipo ∂/∂x¹, ..., ∂/∂xⁿ, per lo spazio tangente T_p(M), allora per ogni vettore o tensore in p otteniamo le sue componenti rispetto a tale base. Se prendiamo un'altra base, le componenti subiscono un cambiamento analogo a quello descritto dalle leggi di trasformazione (6) e (8). Per studiare entità che sono in- varianti rispetto a cambiamenti di base, è utile prendere in considerazione tutte le possibili basi, e questa è precisamente l'idea dei riferimenti mobili di Darboux e Cartan. In ciascun punto p, sia L(M)_p l'insieme di tutti i riferimenti, cioè di tutte le basi di T_p(M). Se fissiamo un particolare riferimento, ogni altro riferimento può essere ottenuto da esso con una trasformazione lineare non singolare. Così L(M)_p è in corrispondenza biunivoca con il gruppo GL(n;R) di tutte le matrici reali n×n con determinante diverso da zero; tale corrispondenza dipende dal riferimento scelto inizialmente. L'unione L(M)=⋃_p∈ML(M)_p può in modo naturale essere considerata una varietà di dimensione n+n² (=dim M+dim GL(n;R)) e si chiama il fibrato dei riferimenti su M. Questo è un esempio, e forse il più importante, di ciò che oggi va sotto il nome di spazio fibrato principale. Analogamente, l'unione T(M)=⋃_p∈MT_p(M) è una varietà di dimensione 2n e si chiama il fibrato tangente di M. Si tratta di un esempio di fibrato vettoriale. Il concetto di spazio fibrato si è rivelato molto proficuo sia in geometria differenziale e in geometria algebrica sia in topologia.

Una metrica riemanniana su M definisce un prodotto interno su ciascuno spazio tangente T_p(M). Tale prodotto si esprime generalmente nella forma

ds²=Σg_ijdxⁱdy^j, (15)

dove (g_ij) è una matrice n×n simmetrica definita positiva che dipende da x¹, ..., xⁿ. Dati due vettori tangenti Σξⁱ∂/∂xⁱ e Σηⁱ∂/∂xⁱ, il loro prodotto interno è allora uguale a Σg_ijξⁱη^j. Se è data una metrica riemanniana, è naturale considerare soltanto riferimenti ortonormali, cioè basi e₁, ..., e_n di T_p(M) costituite da vettori unitari e mutuamente perpendicolari rispetto al dato prodotto interno. Poiché due qualunque riferimenti ortonormali in p differiscono per una trasformazione ortogonale, l'insieme O(M)_p dei riferimenti ortonormali nel punto p può essere messo in corrispondenza biunivoca con il gruppo ortogonale O(n) fissando un riferimento ortonormale (e identificandolo con l'elemento identità del gruppo). L'unione O(M)=⋃_p∈MO(M)_p è un sottofibrato di L(M) corrispondente al sottogruppo O(n)⊂GL(n;R). Così ogni metrica riemanniana ds² su M dà origine a un sottofibrato O(M) di L(M) e questo genera una corrispondenza biunivoca tra l'insieme delle metriche riemanniane su M e l'insieme dei sottofibrati di L(M) corrispondenti al sottogruppo O(n)⊂GL(n;R). Non c'è motivo di restringerci a O(n). Considerando un sottogruppo di Lie arbitrario G di GL(n;R), arriviamo alla nozione di G-struttura. Una G-struttura su M è un sottofibrato di L(M) corrispondente al sottogruppo G⊂GL(n;R). Il concetto è abbastanza generale da includere quasi tutte le strutture geometriche di qualche rilievo, come, per esempio, le strutture complesse, le strutture simplettiche e le foliazioni. Naturalmente, vi sono ben pochi teoremi che siano validi per tutte le G-strutture, ma il concetto è coerente con il programma di Klein di unificare tutte le geometrie dal punto di vista della teoria dei gruppi.

Fra le varie strutture geometriche, le strutture riemanniane e quelle complesse sono le più importanti e di esse ci occuperemo nei prossimi due capitoli.

3. Geometria riemanniana

Una varietà con metrica riemanniana (15) si chiama una varietà riemanniana. L'esempio migliore di varietà riemanniana è una varietà M in uno spazio euclideo R^N. Se M è definito da un sistema di funzioni (1), otteniamo una metrica riemanniana

dove

Da un punto di vista geometrico lo spazio tangente T_p(M) è considerato come un piano n-dimensionale in R^N e la struttura euclidea di R^N induce il prodotto interno su T_p(M) dato dalla (16). Dato che ogni metrica nemanniana su M si può ottenere in questo modo da un immersione in uno spazio euclideo R^N di dimensione sufficientemente alta (J. Nash, 1956), spiegheremo le formule fondamentali della geometria riemanniana supponendo che la metrica sia ottenuta dalla (16). Considerando y^r come una funzione f^r(x¹, ..., xⁿ) di x¹, ..., xⁿ secondo la (1), y=(y¹, ..., y^N) ha il significato di vettore di posizione di M. I vettori tangenti ∂/∂x¹, ..., ∂/∂xⁿ sono rappresentati dai vettori ∂y/∂x¹, ..., ∂y/∂xⁿ in R^N. Come abbiamo indicato nel capitolo precedente, è più naturale considerare un campo di riferimenti ortonormali e₁, ..., e_n. (Un modo di ottenere e₁, ..., e_n è di applicare il cosiddetto processo di ortogonalizzazione di Schmidt a ∂y/∂x¹, ..., ∂y/∂xⁿ). Scrivendo ciascun ∂y/∂xⁱ come combinazione lineare di e₁, ..., e_n e sostituendo in

otteniamo

dove ωⁱ è una 1-forma su M, cosicché risulta

Siano e_n+1, ..., e_N campi di vettori normali unitari a due a due ortogonali. Dato che e_r•e_s=δ_rs (=1 o 0 a seconda che r=s o r≠s), otteniamo

0=d(e_r•e_s)=de_r•e_s+e_r•de_s per r, s=1, ..., N. (21)

Dato che ∂e_r/∂xⁱ è una combinazione lineare di e₁, ..., e_N, possiamo scrivere

dove ωr_s è una 1-forma su M. Sostituendo la (22) nella (21), vediamo che

ωs_r=−ωr_s r, s=1, ..., N, (23)

cioè la matrice (ωs_r) è antisimmetrica. Dalle (19) e (22) abbiamo

Osservando i coefficienti di e_i ed e_α, 1≤i≤n〈α≤N, otteniamo

Analogamente otteniamo dalla (22)

Osservando i coefficienti di e_t, abbiamo

Dato che ω¹, ..., ωⁿ sono linearmente indipendenti (in effetti essi formano la base duale di e₁, ..., e_n), ogni 1-forma è una combinazione lineare di ω¹, ..., ωⁿ in modo univoco. In particolare possiamo scrivere

con

hi^α_j=hj^α_i per α=n+1, ..., N. (30)

Il fatto che hi^α_j sia simmetrico in i e j segue dalla (26). Facendo uso della (23) e sostituendo la (29) nella (28), otteniamo

con

dove R_ijkχ è definita da

Per ottenere le precedenti formule, abbiamo supposto che M fosse immerso in R^N. Ma molte di esse sono effettivamente indipendenti dall'immersione e dipendono solamente dalla metrica ds². Per esempio, definendo ω¹, ..., ωⁿ come la base duale di e¹, ..., e_n, otteniamo ds²=Σn_i=1ωⁱωⁱ. Si può allora mostrare che esiste una e una sola matrice antisimmetrica n×n, (ωi_j)_1≤i,j≤n di 1-forme che soddisfa la (25). Questa matrice di 1-forme (ωi_j) si chiama la forma di connessione di Levi-Civita e la (25) si chiama prima equazione di struttura. (Sebbene l'uso di forme differenziali per questo scopo sia dovuto a E. Cartan, la connessione definita da ds² è dovuta a Levi-Civita). Possiamo definire Ωi_j e R_ijkχ (con R_ijkχ=−R_ijχk) con la (31) indipendentemente dall'immersione; la matrice di 2-forme (Ωi_j) si chiama forma di curvatura e R_ijkχ sono le componenti del tensore di curvatura rispetto alla base e₁, ..., e_n. La (31) si chiama seconda equazione di struttura.

D'altra parte le hi^α_j dipendono dall'immersione e per tale motivo la forma quadratica

si chiama seconda forma fondamentale (si osservi che nella geometria differenziale classica delle superfici ds² si chiama prima forma fondamentale). L'uguaglianza (32) significa che il secondo membro, scritto in termini della seconda forma fondamentale e presumibilmente dipendente dall'immersione, è uguale alla curvatura che dipende solo dalla metrica ds². Questo fatto è noto per superfici nello spazio euclideo 3-dimensionale come theorema egregium di Gauss. Per una superficie, la (31) si riduce a

dω¹₂=Ω¹₂, con Ω¹₂=R₁₂₁₂ω¹⋀ω², (34)

e K=R₁₂₁₂ si chiama curvatura gaussiana della superficie. Ritornando al caso generale, il campo di vettori normali

si chiama vettore di curvatura media. Quando M è una ipersuperficie, cioè N=n+1, il vettore normale e_n+1 e la curvatura media sono ben definiti a meno del segno. Quando il vettore di curvatura media v si annulla identicamente, M viene chiamata una sottovarietà minima. Una interpretazione geometrica della condizione v=0 sarà data più avanti in questo capitolo.

Il calcolo differenziale assoluto di Ricci e Levi-Civita si basa sulla nozione di differenziazione covariante. Dato un campo vettoriale X=Σn_i=1ξⁱe_i su M, il suo differenziale dX=Σn_i=1 (dξⁱe_i+ξⁱde_i)=Σn_i=1 (dξⁱ+Σn_j=1 ξ^jωi_j)e_i+ΣN_λ=n+1 (Σn_j=1ξ^jωj^λ)e_λ non è più tangente ad M e la sua componente tangenziale è il differenziale covariante ∇X di X. Così

Mentre dX fa intervenire vettori normali e dipende dall'immersione, ∇X dipende solo dalla metrica riemanniana ed è un campo tensoriale di tipo (1,1). L'operazione di differenziazione covariante ∇ si estende a campi tensoriali di tutti i tipi così che generalizza l'ordinaria differenziazione di funzioni ed è compatibile con varie operazioni algebriche su campi tensoriali. Così, se K è un campo tensoriale di tipo (r, s), allora ∇K è di tipo (r, s+1). Se X è un campo vettoriale e se f è una funzione definita in M, allora

∇f•X)=df•X+f•∇X. (37)

Il concetto di connessione affine secondo Weyl si basa sulla differenziazione covariante ∇. Per definizione, per ogni campo vettoriale X, ∇X è un campo tensoriale di tipo (1, 1), è lineare in X e soddisfa la (37). Una connessione affine, che non deve necessariamente essere indotta da una metrica riemanniana, dà origine a due importanti campi tensoriali: il campo tensoriale di curvatura e quello di torsione. Quest'ultimo è nullo quando la connessione è indotta da una metrica riemanniana. Una connessione affine definisce la nozione di ‛spostamento parallelo'.

Data una curva x(t) con parametro t, sia x′(t) il suo vettore velocità. Allora si dice che un campo vettoriale X=Σn_i=1ξⁱ(t)e_i, definito lungo la curva x(t), è parallelo se

Un qualunque vettore X_t0 in un generico punto x(t₀) della curva x(t) si estende a un unico campo di vettori paralleli X lungo x(t); questo segue dal fatto che la (38) è un'equazione differenziale ordinaria del primo ordine. In particolare, se x(t), a≤t≤b, è una curva chiusa con inizio in p=x(a)=x(b), lo spostamento parallelo di un riferimento e₁(a), ..., e_n(a) nel punto p lungo la curva x(t) dà luogo a un nuovo riferimento e₁(b), ..., e_n(b) in p. Il nuovo riferimento differisce dal vecchio per una trasformazione lineare (per una trasformazione ortogonale nel caso nemanniano). Mettendo insieme le trasformazioni lineari corrispondenti a tutte le linee chiuse per p, otteniamo un sottogruppo di GL(n;R), detto ‛gruppo di olonomia' della connessione affine. Nel caso riemanniano il gruppo di olonomia è un sottogruppo del gruppo ortogonale O(n). Il gruppo di olonomia misura ‛quanto è curvo lo spazio'; esso è discreto se e solo se lo spazio è localmente piatto. Tuttavia tale gruppo è un invariante molto più debole della curvatura.

La curva x(t) è detta ‛geodetica' se il suo campo vettoriale di velocità x′(t) è parallelo o se la sua curvatura geodetica k_g si annulla, cioè

Formula

Se M è una sottovarietà in uno spazio euclideo R^N, la condizione (39) significa che il campo vettoriale di accelerazione x″(t) è perpendicolare ad M. Quando M stessa è uno spazio euclideo, le geodetiche non sono altro che linee rette. Quando M è una sfera, le geodetiche sono i cosiddetti cerchi massimi. Una geodetica, localmente, è una curva di minima lunghezza, cioè, per ogni t₀, la porzione della curva x(t) da t=t₀ a t=t₀+δ, per δ opportuno, è la più corta curva congiungente x(t₀) e x(t₀+δ). Per essere precisi, sia C_p,q l'insieme delle curve da un punto p a un altro punto q. Sia L la funzione definita su C_p,q che assegna a ogni elemento di C_p,q la sua lunghezza d'arco. Quando una curva è data da xⁱ(t), a≤t≤b, la sua lunghezza è data dall'integrale

Allora una geodetica da p a q è un punto critico di L, cioè un punto di C_p,q dove dL si annulla. La teoria di Morse descrive l'omologia di C_p,q in termini dei punti critici di L e degli indici dell'hessiano di L nei punti critici.

Analogamente, una sottovarietà minima si può ottenere come un punto critico della funzione ‛volume'. Sia S una sottovarietà (k−1)-dimensionale in M e sia C_S l'insieme delle sottovarietà k-dimensionali di M con bordo S. Sia V la funzione definita su C_S che assegna a ogni elemento di C_S il suo volume k-dimensionale. Allora una sottovarietà minima con bordo S è un punto critico di V.

Mentre l'equazione (39) per le geodetiche è un'equazione differenziale ordinaria, le sottovarietà minime sono date come soluzioni di equazioni differenziali non lineari alle derivate parziali. Nel caso classico, cioè per una superficie z=f(x, y) nello spazio euclideo 3-dimensionale, l'equazione differenziale è della forma seguente:

dove

Formula

Per considerare il problema di Plateau, cioè il problema di trovare una sottovarietà minima con bordo assegnato, conviene considerare oggetti geometrici più generali delle sottovarietà differenziabili: le correnti rettificabili di H. Federer e W. Fleming.

Gli spazi C_p,q e C_s sono buoni esempi di varietà a dimensione infinita. Lo studio delle geodetiche, in particolare delle geodetiche chiuse, è uno dei campi in cui la teoria delle varietà a dimensione infinita ha avuto un notevole successo.

4. Varietà complesse e varietà kähleriane

Sostituendo nella definizione di una varietà (reale) lo spazio euclideo reale Rⁿ con lo spazio euclideo complesso Cⁿ e le funzioni differenziabili con le funzioni olomorfe (cioè analitiche complesse), si arriva alla definizione di ‛varietà complessa'. Così una varietà complessa M è ricoperta da sottoinsiemi U_α, ciascuno dei quali è in corrispondenza biunivoca con un dominio D_α, di Cⁿ. Mediante questa corrispondenza si hanno funzioni coordinate (z¹_α, ..., zn_α) su U_α corrispondenti alle coordinate (z¹, ..., zⁿ) in D. Nell'intersezione U_α⋂U_β i cambiamenti di coordinate zk_β=fk_βα (z¹_α, ..., zn_α) sono, per definizione, olomorfi.

Un dominio in Cⁿ è chiaramente una varietà complessa ricoperta da un singolo intorno coordinato. Uno spazio proiettivo complesso P_n(C) di dimensione n è una varietà complessa compatta ricoperta da n+1 intorni coordinati, ciascuno dei quali è in corrispondenza biunivoca con Cⁿ nella seguente maniera. Esso è definito come l'insieme delle rette complesse uscenti dall'origine in Cⁿ⁺¹; così un punto di P_n(C) è dato dall'insieme {(ta⁰, ta¹, ..., taⁿ); t∈C}, dove (a⁰, a¹, ..., aⁿ) è un fissato elemento di Cⁿ⁺¹ diverso da zero. Per ogni α, 0≤α≤n, sia U_α l'insieme dei punti di P_n(C) con a^α≠0. Allora P_n(C) è ricoperto da U₀, U₁, ..., U_n. A ogni punto di U_α rappresentato dalla retta per (a⁰, a¹, ..., aⁿ) si assegna un punto (a⁰/a^α, ..., a^α-1/a^α, a^α+1/a^α, ..., aⁿ/a^α) di Cⁿ. Questo stabilisce una corrispondenza biunivoca tra U_α e Cⁿ. Lo spazio proiettivo 1-dimensionale P₁(C) è la cosiddetta sfera di Riemann e può essere ottenuto aggiungendo un ‛punto all'infinito' al piano gaussiano C.

Dato che ogni punto di P_n(C) può essere rappresentato da un elemento non nullo di Cⁿ⁺¹ (a meno di un fattore complesso diverso da zero), conviene usare le coordinate (Z⁰, ..., Zⁿ⁺¹) di Cⁿ⁺¹ come coordinate ‛omogenee' di P_n(C). Se g₁, ..., g_r sono polinomi omogenei di Z⁰, ..., Zⁿ⁺¹, allora i loro zeri comuni, cioè le soluzioni delle equazioni

g₁=0, ..., g_r=0, (42)

definiscono un insieme algebrico. Un insieme algebrico non singolare o regolare è una varietà complessa e si chiama ‛varietà algebrica' (proiettiva).

Sia M una varietà complessa con coordinate locali z¹, ..., zⁿ (quando consideriamo un singolo intorno coordinato U_α omettiamo l'indice α in z¹_α, ..., zn_α); lo spazio vettoriale tangente complesso di M è spazzato da ∂/∂z¹, ..., ∂/∂zⁿ e dai loro coniugati ∂/∂ÿ¹, ..., ∂/∂ÿⁿ. Le forme differenziali complesse su M sono generate da dz¹, ..., dzⁿ, dÿ¹, ..., dÿⁿ. Una metrica riemanniana su M è detta hermitiana se definisce un prodotto interno hermitiano su ciascuno spazio tangente. Una metrica hermitiana si può esprimere nella forma

ds²=2Σg_j-kdz^jdÿ^k, (43)

dove (g_j-k) è una matrice n×n hermitiana definita positiva che dipende da z¹, ..., zⁿ. La connessione di Levi-Civita di M, cioè la differenziazione covariante ???30??? su M come varietà riemanniana, può conservare oppure non conservare la struttura complessa di M; quando la conserva, la metrica hermitiana ds² è detta ‛metrica di Kähler'. Associamo alla metrica hermitiana (43) una forma differenziale esterna

Φ=√-−-1 Σg_j-kdz^j⋀dÿ^k; (44)

questa forma si chiama generalmente la ‛forma di Kähler associata'. La (43) è una metrica di Kähhler se e solo se la forma di Kähhler Φ è chiusa, cioè se dΦ=0.

Possiamo costruire sullo spazio proiettivo P_n(C) una metrica di Kähler usando le coordinate locali z¹, ..., zⁿ in U_α. Definiamo

ds²=2Σg_j-kdz^jdÿ^k,

dove

g_j-k=∂² log (1+Σ∣zⁱ∣²)/∂z^j∂ÿ^k. (45)

Questa metrica localmente definita è effettivamente ben definita globalmente su P_n(C) ed è nota sotto il nome di metrica di Fubini-Study. Generalmente una sottovarietà complessa di una varietà kähleriana eredita la metrica ed è anch'essa una varietà kähleriana. In particolare, ogni varietà algebrica proiettiva è kähleriana.

Sia M una varietà kähleriana compatta di dimensione n. Dato che la forma kähleriana Φ è chiusa, anche le sue potenze esterne Φ², ..., Φⁿ sono chiuse. In base al teorema di de Rham, Φ^k definisce un elemento del gruppo di coomologia H^2k(M;R) (=H²_R^k(M)). Dato che la più alta potenza Φⁿ dà l'elemento di volume, essa definisce un elemento non nullo di H²ⁿ(M;R)=R. Perciò Φ, Φ², ..., Φⁿ definiscono tutte classi di coomologia non nulle. In particolare, i numeri di Betti a dimensione pari di una varietà kähleriana compatta sono tutti positivi. Si può usare questo fatto per mostrare che alcune varietà complesse compatte non sono varietà kähleriane. Ma la teoria di Hodge dà risultati molto più dettagliati.

Dato che il secondo numero di Betti di P_n(C) è 1, un opportuno multiplo diverso da zero di Φ definisce un elemento del gruppo di coomologia intera H²(P_n(C);Z). Quindi la stessa cosa è vera per tutte le varietà algebriche proiettive. Il teorema fondamentale di Kodaira (1954) mostra viceversa che se una varietà complessa compatta ammette una metrica kähleriana la cui forma di Kähler associata definisce una classe di coomologia intera, allora essa è una varietà algebrica proiettiva. La geometria di Kähler occupa così una posizione unica nella geometria differenziale grazie ai suoi stretti legami con la geometria algebrica.

Varietà kähleriane non compatte sono anch'esse ugualmente importanti per il loro ruolo nella teoria delle funzioni, nella teoria delle rappresentazioni unitarie, ecc. Nel disco unitario D={z∈C;∣z∣〈1} esiste una particolare metrica kähleriana

che risale a Poincaré. Questa metrica ha una curvatura negativa costante ed è, in un certo senso, duale della metrica di Fubini-Study sulla sfera riemanniana, che ha curvatura positiva costante. La metrica di Poincaré è un caso particolare della metrica di Bergman che si può definire su ogni dominio limitato M in Cⁿ nel modo seguente. Sia H lo spazio di Hilbert di funzioni olomorfe di quadrato sommabile su M e sia f₀, f₁, f₂, ... una base ortonormale completa per H. La funzione nucleo di Bergman K(z, ÿ) è definita dalla

K(z, ÿ)=Σ∣f_j(z)∣² (47)

e la metrica di Bergman è data dalla

ds²=2Σg_j-kdz^jdÿ^k, dove g_j-k=∂² log k/∂z^j∂ÿ^k. (48)

La scoperta di questa metrica biolomorficamente invariante fatta da S. Bergman nel 1933 aprì un nuovo capitolo nella geometria di più variabili complesse.

Si dice che un dominio limitato M è simmetrico se in ogni punto z di M c'è una simmetria σ²_z, cioè un automorfismo olomorfo di M di ordine 2(σ²_z=identità) avente z come punto fisso isolato. Il campo del tensore di curvatura della metrica di Bergman per un dominio limitato simmetrico è parallelo. La classe dei domini limitati simmetrici scoperta e classificata da É. Cartan gioca un importante ruolo in differenti campi della matematica. Il semipiano superiore generalizzato S_n di Siegel, consistente in matrici complesse simmetriche Z di grado n con parte immaginaria definita positiva, è forse il dominio simmetrico più importante per le sue applicazioni alla teoria dei numeri attraverso le forme modulari. (Nonostante il fatto che S_n non sia limitato, esso è equivalente a un dominio limitato esattamente come il semipiano superiore ordinario in C è ‛conformemente' equivalente al disco unitario).

L'operatore di differenziazione esterna d su una varietà complessa M si decompone in due operatori ∂ e -∂:

Dato che le forme differenziali complesse sono generate da dz¹, ..., dzⁿ, dÿ¹, ..., dÿⁿ, esse sono bigraduate mediante i gradi dei dzⁱ e dÿⁱ. Così -∂ manda una forma di grado (p, q) in una forma di grado (p, q+1). Da d²=0 segue che ∂²=0. Il gruppo di coomologia di Dolbeault o il gruppo di -∂-coomologia H^p,q(M;C) di grado (p, q) è, per definizione, il quoziente dello spazio delle (p, q)-forme -∂-chiuse per lo spazio delle (p, q)-forme -∂-esatte. Una p-forma olomorfa, cioè una (p, 0)-forma

ϕ=Σf_i1 ... _ip dzⁱ₁⋀...⋀dzⁱ_p (50)

con coefficienti olomorfi f_i1 ... _ip, è annullata da-∂. H^p,0(M;C) è quindi isomorfo allo spazio delle p-forme olomorfe. Data una metrica hermitiana su M, otteniamo la teoria -∂-armonica come nel caso riemanniano. Quando M è una varietà kähleriana compatta, i gruppi di -∂-coomologia sono legati ai gruppi di coomologia di de Rham dalla

H^r(M;C)=Σ_p+q=r H^p,q(M;C). (51)

Allo scopo di avere una teoria di coomologia soddisfacente su una varietà complessa, è necessario estendere il coefficiente da C a vari fasci. Un fascio S su M assegna, per definizione, a ciascun sottoinsieme aperto U di M un gruppo abeliano o, più in generale, un modulo S(U) in modo tale che, se V è un insieme aperto più piccolo, allora esiste una restrizione rU_V:S(U)→S(V). Questi moduli S(U) e le restrizioni rU_V devono soddisfare certe condizioni naturali. Un buon esempio è il fascio Ω^p delle p-forme olomorfe su una varietà complessa M; per ogni sottoinsieme aperto U di M, Ω^p(U) è definito come l'insieme delle p-forme olomorfe su U. La teoria di coomologia con coefficienti in un fascio, sviluppata da J. Leray, è diventata uno strumento fondamentale in topologia, nella teoria delle funzioni di più variabili complesse, in geometria algebrica e in geometria differenziale. Il gruppo di coomologia H^p(M;S) è definito nello stesso modo in cui è definito il gruppo di coomologia di Čech ordinario. Così H^q(M;C) può essere considerato il q-mo gruppo di coomologia di M con coefficienti nel fascio delle funzioni costanti (a valori complessi). L'analogo complesso del teorema di de Rham è il seguente isomorfismo di Dolbeault:

H^p,q(M;C)≅H^q(M;Ω^p). (52)

I teoremi di de Rham e di Dolbeault sono fondamentali per usare metodi di geometria differenziale in problemi coomologici di varietà.

5. Classi caratteristiche

Sia M una superficie con metrica riemanniana e sia K la sua curvatura gaussiana definita dalla (34). Se R è una regione semplicemente connessa di M avente come contorno una curva regolare C, cioè una regione che si può ridurre a un punto per contrazioni continue di C, la formula di Gauss-Bonnet esprime ‛l'integrale di curvatura' ∫_RKω¹⋀ω² mediante l'integrale di linea ∫_Ck_g, della curvatura geodetica k_g di C definita nella (39):

∫_Ck_g+∫_RKω¹⋀ω²=2π. (53)

Se M è una superficie orientabile chiusa, allora la (50) implica

∫_Mkω¹⋀ω²=2π•χ(M), (54)

dove χ(M) è il numero di Eulero di M. Se suddividiamo M in f triangoli (o facce) e otteniamo v vertici ed e spigoli, allora χ(M) è dato da

χ(M)=v−e+f. (55)

Alternativamente, se b_i è l'i-mo numero di Betti di M, cioè b_i=dim Hⁱ(M;R), allora

χ(M)=b₀−b₁+b₂=2−b₁. (56)

La formula di Gauss-Bonnet (54) mostra che un invariante topologico χ(M) può essere espresso come l'integrale di un invariante geometrico locale K/2π.

Se M è una varietà orientabile chiusa di dimensione n, il suo numero di Fulero è definito sia come la somma alternata dei numeri s_i dei simplessi i-dimensionali di una triangolazione di M, sia come la somma alternata degli i-mi numeri di Betti b_i=dim Hⁱ(M;R):

A causa della dualità di Poincaré, cioè b_i=b_n-i, il numero di Eulero si annulla quando n è dispari. Supponiamo che n sia pari, n=2p. Sia Ω=(Ωi_j) la forma di curvatura di una metrica riemanniana su M. Allora il teorema generalizzato di Gauss-Bonnet stabilisce:

dove ε_i1 ... _in è il segno della permutazione (i₁, ..., i_n).

Il fatto che l'integrando della (58) è indipendente dalla scelta di un campo di riferimento ortonormale e₁, ..., e_n ed è ben definito globalmente su M è una conseguenza del seguente risultato generale sui polinomi invarianti e sulle classi caratteristiche. Sia SO(n) il gruppo di matrici ortogonali n×n con determinante 1 e sia so(n) la sua algebra di Lie costituita da matrici n×n antisimmetriche. Sia f un polinomio omogeneo di grado r definito su so(n) e invariante in questo senso:

f(UXU^-1)=f(X) per X∈so(n) e U∈SO(n). (59)

Dato che la forma di curvatura Ω=(Ωi_j) è una 2-forma a valori in so(n), f(Ω) è una forma differenziale di grado 2r. Il risultato generale è che f(Ω) è una 2r-forma chiusa ben definita globalmente su M, indipendentemente dalla scelta della base ortonormale e₁, ..., e_n. Se n è dispari, il determinante di X=(Xi_j)∈so(n) si annulla sempre. Ma se n è pari, il determinante di X è il quadrato del seguente polinomio:

g(X)=Σε_i1 ... _in Xi_i¹₂ ... Xi_in_n^-1. (60)

A meno di un fattore costante, g è il polinomio che appare nella (58).

Ci sono altri polinomi invarianti di grande interesse. Si definiscono polinomi invarianti omogenei p_i, i=1, ..., [n/2], di grado 2i come

La classe di coomologia definita dalla 4i-forma p_i(Ω) è detta i-ma classe di Pontrjagin di M. La definizione (61) è valida quando X è una qualunque matrice n×n. I polinomi p₁, p₂, ... sono invarianti nel senso della (59) anche quando U è un'arbitraria matrice non singolare. Questo significa, dal punto di vista della geometria differenziale, che le classi di Pontrjagin possono essere definite mediante la curvatura di un'arbitraria connessione affine. Questo non è il caso per la classe di Eulero, dato che g è invariante solo rispetto a SO(n).

Per una varietà complessa M con una metrica hermitiana, la forma di curvatura Ω=(Ωi_j) è antihermitiana, cioè essa assume i valori nell'algebra di Lie del gruppo unitario U(n). Come nella (61), poniamo

Allora c_i(Ω) è una 2i-forma chiusa su M e la sua classe di coomologia è la i-ma classe di Chern di M.

Allo scopo di avere una soddisfacente teoria delle classi caratteristiche, è essenziale considerare fibrati vettoriali generali e fibrati tangenti e cotangenti. Un fibrato vettoriale E su una varietà M è, grosso modo, una famiglia di spazi vettoriali parametrizzata differenziabilmente dallo spazio di base M. Così a ciascun punto x di M si associa uno spazio vettoriale E_x di dimensione fissa, sia per esempio r. Inoltre E deve essere localmente banale in questo senso. Lo spazio di base M è ricoperto da insiemi aperti U_α e ogni elemento ξ∈E_x con x∈U_α ha componenti (ξ¹_α, ..., ξr_α)∈R^r. Se x è anche in U_β, le componenti (ξ¹_β, ..., ξr_β) si devono ottenere mediante una trasformazione lineare t_βα(x) dalle (ξ¹_α, ..., ξr_α). Questa è una generalizzazione della situazione in cui un vettore tangente si esprime con le sue componenti rispetto a un sistema di coordinate locale e la matrice jacobiana di un cambiamento di coordinate fa le veci di t. La funzione a valori matriciali t_βα su U_α⋂U_β, è detta funzione di transizione. Quando le fibre E_x sono spazi vettoriali complessi e le funzioni di transizione t_βα sono trasformazioni lineari complesse, E è detto fibrato vettoriale complesso. Inoltre, se M è una varietà complessa e le t_βα sono olomorfe, E è detto fibrato vettoriale olomorfo. Un fibrato vettoriale olomorfo con fibra di dimensione i si dice fibrato di rette complesso e ha un ruolo particolarmente importante in geometria algebrica per i suoi stretti legami con i divisori.

Concetti della geometria differenziale quali il concetto di metrica riemanniana o hermitiana, il concetto di connessione e di curvatura si generalizzano a fibrati vettoriali. Allora la classe di Eulero, le classi di Pontrjagin e le classi di Chern di un fibrato vettoriale si possono rappresentare mediante forme differenziali chiuse che si esprimono mediante le forme di curvatura.

Il fascio Ω^p delle p-forme olomorfe si generalizza nel fascio Ω^p(E) delle p-forme olomorfe con coefficienti in un fibrato vettoriale olomorfo E, cosicché Ω^p coincide con Ω^p(E) quando E è il fibrato di rette banale. Allora χ_p(M;E)=Σ(−1)ⁱ dim Hⁱ(M;Ω^p(E)) è una specie di numero di Eulero e il teorema di Riemann-Roch-Hirzebruch esprime χ_p(M;E) mediante le classi di Chern di E e di M quando M è una varietà algebrica. Questo risultato è stato generalizzato da Atiyah e Singer.

Sia A:Γ(W)→Γ(W′) un operatore differenziale ellittico, dove Γ(W) e Γ(W′) indicano gli spazi delle sezioni dei fibrati vettoriali W e W′ su una varietà compatta M. Allora sia il nucleo che il conucleo di A hanno dimensione finita e l'indice di A, definito dalla:

indice(A)=dim kerA−dim cokerA, (63)

si può ottenere integrando un certo polinomio delle classi caratteristiche di W, W′ ed M sulla varietà M. Per esempio, se si indica lo spazio delle (p, q)-forme su una varietà complessa compatta M con A^p,q(M), allora

-∂+-∂*:ΣA^0,2p(M)→ΣA^0,2p+1(M) (64)

è un operatore ellittico. (Qui -∂* indica l'aggiunto di -∂ rispetto a una metrica hermitiana di M). L'indice di questo operatore è uguale a χ₀(M,C)=Σ(−1)ⁱ dim Hⁱ(M;Ω⁰), dove C a primo membro sta per il fibrato di rette banale; χ₀(M;C) si chiama ‛genere aritmetico' di M.

Sia il teorema di Riemann-Roch-Hirzebruch che il teorema dell'indice di Atiyah-Singer furono dapprima dimostrati con metodi topologici, e precisamente usando la teoria del cobordismo di Thom. Grazie agli sforzi congiunti di Atiyah, Bott, Gilkey e Patodi, si ha ora una nuova dimostrazione che usa metodi della geometria differenziale; essa fa uso delle identità di Bianchi sulla curvatura anziché del cobordismo.

6. Sviluppi della geometria differenziale

Tutti i rami della matematica, e quindi tutti i campi della scienza, crescono per forze interne e per stimoli esterni. La geometria differenziale non fa eccezione. Man mano che si è sviluppata al di là del proprio campo (curve, superfici e varietà riemanniane), i suoi confini con i campi limitrofi sono diventati meno chiari. Fin dalle sue origini la geometria differenziale ha avuto stretti legami con la topologia, come si può vedere dalla formula di Gauss-Bonnet. Questi legami si sono rafforzati con la teoria di Morse e, più recentemente, con le classi caratteristiche. Le superfici minime hanno portato la geometria differenziale a contatto con le equazioni alle derivate parziali e con le funzioni di variabile complessa. La recente dimostrazione del teorema dell'indice di Atiyah-Singer citata nel cap. 5 ha fatto sì che la geometria differenziale costituisca anche un ponte tra la topologia e l'analisi. La teoria della distribuzione dei valori di Nevanlinna e le sue generalizzazioni successive possono essere più agevolmente descritte mediante la geometria differenziale. La geometria differenziale ha arricchito la geometria algebrica attraverso le varietà kähleriane e viceversa. Essa ha dei legami, se pure un po' distanti, con la teoria dei numeri, attraverso le forme automorfe su domini simmetrici. Non esisterebbe una teoria della relatività generale senza la geometria riemanniana. Le strutture simplettiche e di contatto hanno trovato sviluppo nella meccanica. Si può dire che non vi sia campo della matematica che non sia stato toccato dalla geometria differenziale. Questo non deve sorprendere dato che quasi tutte le costruzioni matematiche hanno luogo su varietà di un tipo o di un altro e la geometria differenziale è calcolo su varietà. Quantunque argomenti quali sottovarietà minime, varietà riemanniane a curvatura positiva e geodetiche appartengano alla geometria riemanniana vera e propria e siano oggi attivi campi di ricerca, la geometria differenziale ha acquisito una maggiore importanza come metodo, linguaggio e modo di pensare in altri campi della matematica. Essa deve il suo successo in gran parte al concetto unificatore di curvatura introdotto da Gauss e da Riemann.

bibliografia

Alexandrov, A. D., Die innere Geometrie der konvexen Flächen, Berlin 1955.

Atiyah, M., Bott, R., Patodi, V. K., On the heat equation and the index theorem, in ‟Inventiones mathematicae", 1973, XIX, pp. 279-330.

Berger, M., Gauduchon, P., Mazet, E., Le spectre d'une variété riemannienne, Berlin 1971.

Bianchi, L., Lezioni di geometria differenziale, Pisa 1894.

Blaschke, W., Vorlesungen über Differentialgeometrie, Berlin 1945.

Cartan, É., Leçons sur la géométrie des espaces de Riemann, Paris 1946.

Chern, S. S., The geometry of G-structures, in ‟Bulletin of the American Mathematical Society", 1966, LXXII, pp. 167-219.

Darboux, G., Théorie générale des surfaces, voll. I-IV, Paris 1888-1896.

Eisenhart, L. P., Non-Riemannian geometry, in ‟American Mathematical Society colloquium publication", 1927, VIII.

Eisenhart, L. P., Riemannian geometry, Princeton 1949.

Gromoll, D., Klingenberg, W., Meyer, W., Riemannsche Geometrie im Grossen, Berlin 1968.

Helgason, S., Differential geometry and symmetric spaces, New York 1962.

Hirzebruch, F., Topological methods in algebraic geometry, Berlin 1966.

Hodge, W. V. D., The theory and applications of harmonic integrals, Cambridge, Mass., 1952.

Kobayashi, S., Transformation groups in differential geometry, Berlin 1972.

Kobayashi, S., Nomizu, K., Foundations of differential geometry, vol. I, New York 1963, vol. II, New York 1969.

Levi-Civita, T., The absolute differential calculus, London 1926.

Lichnerowicz, A., Théorie globale des connexions et des groupes d'holonomie, Roma 1955.

Lichnerowicz, A., Géométrie des groupes de transformations, Paris 1958.

Milnor, J. W., Lectures on Morse theory, Princeton 1963.

Morrow, J., Kodaira, K., Complex manifolds, New York 1971.

Ossermann, R., A survey of minimal surfaces, New York 1969.

Rham, G. de, Variétés différentiables, Paris 1955.

Ricci-Curbastro, G., Levi-Civita, T., Méthodes de calcul différentiel absolue et leurs applications, in ‟Mathematische Annalen", 1900, LIV, pp. 125-201.

Weil, A., Introduction à l'étude des variétés kähleriennes, Paris 1958.

Yano, K., Bochner, S., Curvature and Betti numbers, Princeton 1953.