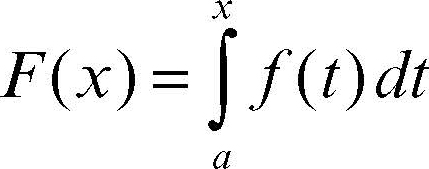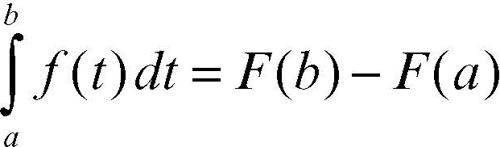calcolo integrale, teorema fondamentale del

calcolo integrale, teorema fondamentale del

calcolo integrale, teorema fondamentale del lega la nozione di integrale definito a quella di integrale indefinito, riducendone il calcolo analitico in molti casi alla determinazione di una primitiva della funzione integranda. Il teorema, nella sua forma più semplice, stabilisce che se ƒ è una funzione continua, una sua primitiva è data dalla funzione, indicata con F, così definita:

cioè F è derivabile e F ′(x) = ƒ(x) (a è fisso e l’integrale è pensato come funzione dell’estremo x variabile). Questo risultato, noto appunto come teorema fondamentale del calcolo integrale, stabilisce una connessione tra integrale e derivata: nel caso di funzioni continue le operazioni di derivazione e di integrazione si possono considerare l’una l’inversa dell’altra. Il teorema consente così il calcolo immediato dell’integrale definito, e, quindi, la determinazione dell’area al di sotto del grafico di una funzione in un intervallo [a, b] ove essa è definita e limitata, senza operazioni di passaggio al limite della somma delle aree dei corrispondenti rettangoli costruiti a partire dalle suddivisioni di tale intervallo. L’integrale definito si ottiene infatti, per il teorema fondamentale del calcolo integrale, mediante la formula

essendo F una qualunque primitiva di ƒ. Questa formula è comunemente nota come formula di Newton-Leibniz (alcuni autori riportano i cognomi dei due matematici in ordine alfabetico a sottolineare l’uguale rilevanza del contributo di ciascuno di essi). Formulazioni più deboli del teorema valgono anche nel caso di funzioni integrabili secondo Riemann o secondo Lebesgue, per cui il teorema si estende, nella forma sopra descritta, ai soli punti in cui ƒ(x) è continua o prolungabile con continuità. Il teorema è anche noto come teorema di Torricelli-Barrow.