Cardano

Cardano

Cardano Girolamo (Pavia 1501 - Roma 1576) medico, matematico, filosofo. Addottoratosi in medicina a Padova nel 1526, insegnò matematica a Milano a partire dal 1543 praticando nel contempo la professione di medico, sia pure in forme irregolari, in quanto l’esercizio ufficiale gli era vietato dalla corporazione dei medici a causa della sua condizione di figlio illegittimo. La sua fama di medico, da lui stesso abilmente propagandata con toni magico-taumaturgici, oltrepassò ben presto i confini dell’Italia: fu richiesto come medico di corte in Danimarca e a Edimburgo per curare l’arcivescovo J. Hamilton. Dal 1547 al 1551 insegnò medicina nell’università di Pavia, e dal 1562 in quella di Bologna. Le libere opinioni e le credenze astrologiche enunciate esplicitamente nelle sue opere ne provocarono l’arresto da parte dell’Inquisizione nel 1570; fu liberato nello stesso anno per intercessione del cardinale Carlo Borromeo. Trasferitosi nel 1571 a Roma, dove ottenne un vitalizio dal papa, vi trascorse gli ultimi anni. Cardano incarna, sia pure in dimensioni ridotte rispetto ad altre grandi figure del rinascimento, l’ideale dell’«uomo universale», che estende la propria indagine a tutti i campi dello scibile, passando dalla metafisica alla medicina, dalle scienze della natura alla matematica, dall’astronomia alle scienze occulte e alla tecnologia. Nel naturalismo di Cardano, ispirato a una concezione neoplatonica del mondo cui non sono estranee suggestioni dell’aristotelismo padovano, le osservazioni empiriche si intrecciano a elucubrazioni occultistiche nella ricerca dei nessi di simpatia e antipatia che legano fra di loro le parti dell’universo riducendo a unità il molteplice. Particolare rilievo ha nel suo pensiero la matematica che, per essere costruzione della mente umana, garantisce un sapere di gran lunga più certo di quello fornito dalla conoscenza sensibile; ma questa esaltazione della matematica non si traduce ancora in quella matematizzazione della ricerca scientifica da cui nascerà la scienza moderna. Nella vastissima produzione letteraria di Cardano spiccano il De subtilitate (1547) e il De rerum varietate (1557), e la pregevole autobiografia (De vita propria, 1575), documento di grande interesse sulla cultura del rinascimento italiano. Sempre assillato da problemi economici di sopravvivenza, fu un appassionato cultore del gioco d’azzardo, di cui studiò ed enunciò i principi (ma anche i trucchi per barare), nel Liber de ludo aleae (1560), che si può considerare uno dei primi testi che analizzano in modo sistematico la teoria della probabilità. Oltre che per l’invenzione di un particolare apparato meccanico snodabile usato in numerose applicazioni (il giunto cardanico, che permette di trasferire il moto rotatorio di un asse su un asse di direzione diversa), la fama di Cardano è principalmente legata al trattato Ars magna (1545), in cui sono contenute le formule risolutive, per mezzo di radicali, delle equazioni algebriche di terzo e quarto grado (→ Cardano, formule di). La pubblicazione di queste formule dette luogo a una lunga disputa sulla priorità della scoperta. Pare infatti che Cardano per la soluzione dell’equazione cubica avesse usufruito, sotto vincolo di segretezza, di decisivi suggerimenti da parte di Tartaglia, che ancora nulla aveva pubblicato sull’argomento ma aveva a sua volta ripreso la formula da Scipione Dal Ferro, vero scopritore della soluzione; anche per la formula dell’equazione di quarto grado Cardano si rifaceva a una scoperta del suo allievo Ludovico Ferrari. La decennale disputa tra Cardano e Tartaglia, di controversa ricostruzione storica nei dettagli, testimonia comunque il vivace fermento dell’Italia rinascimentale anche negli studi matematici e scientifici.

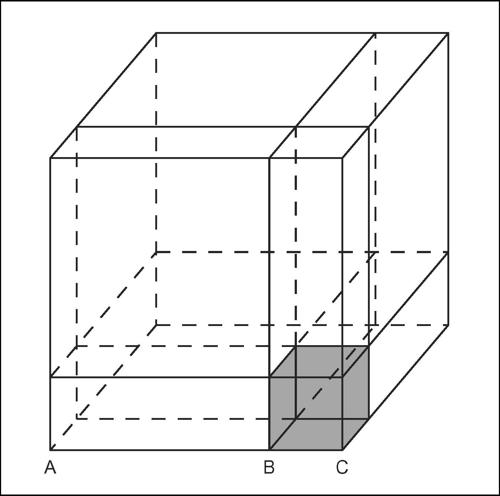
Non ancora svincolatosi dalle commistioni algebrico-geometriche della matematica prerinascimentale, Cardano concepiva le equazioni numeriche secondo una prospettiva geometrica. Egli fornì le formule per le equazioni polinomiali di terzo grado ricorrendo a un metodo che può essere oggi definito come metodo del completamento al cubo. Tali formule possono infatti ottenersi geometricamente osservando che se a un segmento AC si toglie un segmento BC allora il cubo di spigolo {{{1}}}− BC) risulta uguale al cubo di spigolo AC, meno il cubo di spigolo BC, meno tre volte il parallelepipedo rettangolo di spigoli {{{1}}}− BC), AC e BC, cioè il parallelepipedo di base BC · AB e altezza AC:

Questa espressione è la versione geometrica di ciò che algebricamente è chiamato cubo del binomio. Posto

risulta:

da cui, posto u – v = q e uv = (p/3)³, si ottiene x³ = q − px e, quindi, x³ + px = q.