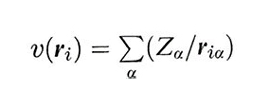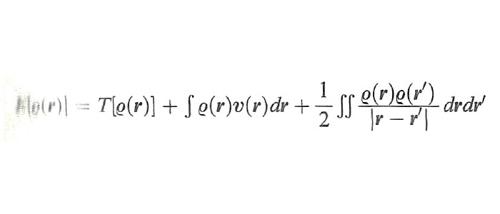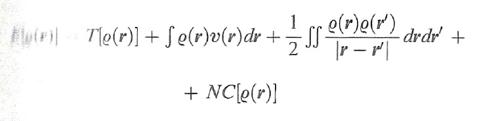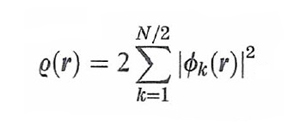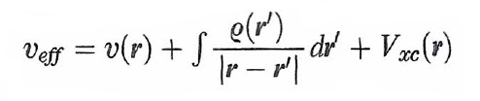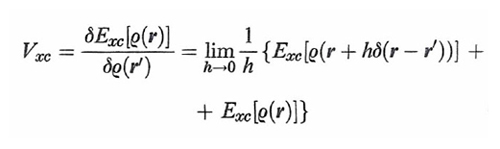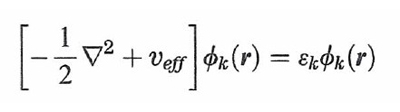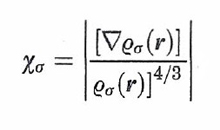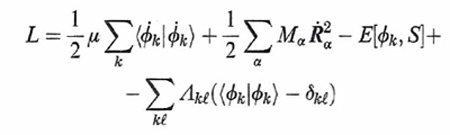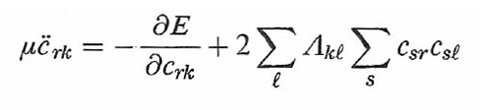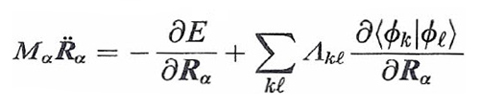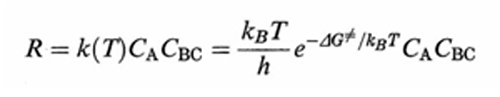Chimica computazionale
Chimica computazionale
sommario: 1. Introduzione. 2. Presupposti teorici. 3. Stati e orbitali atomici. 4. Spin-orbitali, antisimmetria e legame chimico. 5. Il modello di Hartree-Fock del campo autocompatibile. 6. Ruolo della correlazione elettronica. 7. Metodi semiempirici. 8. Metodo del funzionale della densità. 9. Cinetica e dinamica delle reazioni chimiche. 10. Conclusioni. □ Bibliografia.
1. Introduzione
"Forse non siamo molto lontani dal tempo in cui saremo in grado di descrivere i fenomeni dell'intera chimica mediante i calcoli". Questa osservazione fatta da Joseph Louis Gay-Lussac in uno scritto dell'inizio dell'Ottocento (Sur la combinaison des substances gazeuses les unes avec les autres), prima che fossero disponibili le conoscenze scientifiche che sarebbero state necessarie per perseguire lo scopo da essa anticipato, acquista attualmente una connotazione profetica. In termini concreti, questa prospettiva è affiorata nella prima metà del Novecento con l'avvento della meccanica quantistica, la quale, dopo essere passata attraverso una fase di definizione concettuale che ha ridisegnato il volto della chimica, è ormai entrata in una fase operativa, essendo stati acquisiti gli strumenti per valutare con accuratezza la struttura e l'energia delle molecole sia quando sono isolate, sia quando collidono per dare origine a nuovi composti. Il riconoscimento del grande progresso conseguito nell'applicazione della meccanica quantistica alla soluzione dei problemi relativi alla struttura e alla trasformazione delle molecole è infatti testimoniato dall'attribuzione del premio Nobel per la chimica, nel 1998, a due scienziati che a tale progresso hanno contribuito in modo determinante: Walter Kohn e John Pople. Anche se questo approccio allo studio dei problemi chimici, detto computazionale, può sembrare troppo 'illuministico' perché intacca il tradizionale carattere naturalistico e sperimentale della chimica, esso sta in realtà acquistando un ruolo sempre più rilevante non solo nella chimica moderna, ma anche in molti settori scientifici e tecnologici a essa connessi. Infatti, se fino a qualche anno fa i chimici teorici si dovevano accontentare di riprodurre dati sperimentali già noti, oggi possono con cautela avventurarsi nella previsione di dati utili a orientare le indagini nei casi in cui le informazioni sperimentali dettagliate siano carenti, in settori quali le sintesi chimiche, i processi di combustione, la catalisi, la chimica ambientale e atmosferica, la preparazione di materiali tecnologicamente avanzati, la biologia molecolare, la chimica cosmica e altri ancora.
In realtà, la rilevanza che sta acquistando la chimica computazionale trae vantaggio anche dallo sviluppo di metodologie e di tecniche sperimentali che permettono di ottenere informazioni sempre più accurate e dettagliate sulla struttura delle molecole, sulle transizioni energetiche cui sono soggette e sulla dinamica dei loro movimenti derivanti dalle interazioni con altre molecole. Significativi a tale proposito sono i risultati ottenuti da Ahmed H. Zewail (v., 1996), premio Nobel per la chimica nel 1999, mediante l'impiego di laser che, grazie alla produzione di impulsi dell'ordine dei femtosecondi (10-l5s), consentono di investigare i dettagli delle reazioni chimiche attraverso l'analisi del comportamento dei reagenti per un tempo così breve da permettere di cogliere le caratteristiche geometriche e dinamiche dei complessi molecolari che si formano nell'atto di collisione dei reagenti stessi. La sinergia fra risultati sperimentali così sofisticati e la loro interpretazione mediante dettagliati calcoli teorici conferisce alla chimica un rinnovato slancio, non solo sul piano concettuale ma anche nelle applicazioni su tematiche di frontiera come quelle precedentemente menzionate.
2. Presupposti teorici
Verso la metà degli anni venti dello scorso secolo risultava ormai certo che il mondo era costituito da nuclei atomici e da elettroni, i quali, interagendo, formano gli atomi e le molecole; questi ultimi, a loro volta, danno origine alla materia inorganica, organica e biologica che ci circonda e di cui siamo formati, e il loro comportamento sta alla base delle principali funzioni che governano i processi naturali. Non solo: anche le regole per descrivere tale comportamento erano ormai ben conosciute, per cui si apriva uno sconfinato campo di indagini derivante dalle loro applicazioni, tanto da indurre Paul Dirac, uno dei padri della meccanica quantistica, ad affermare nel 1929: "Le leggi fisiche fondamentali necessarie per la teoria matematica dell'intera chimica sono ormai completamente note, e la difficoltà è dovuta solo al fatto che la loro applicazione porta a equazioni troppo complicate per essere solubili" (P. Dirac, Quantum mechanics of many-electron systems, in "Proceedings of the Royal Society (London)", 1929, CXXIII, p. 714). Secondo le parole pronunciate da Pople nella Nobel lecture, l'esame retrospettivo della frase precedente appare "come un grido di trionfo e di disperazione", poiché essa preannunciava l'avvento di un colossale sforzo matematico. In questo senso la chimica computazionale si può allora considerare come la realizzazione in parte conseguita, ma comunque ancora in via di svolgimento, del programma implicitamente enunciato da Dirac.
Non ci soffermeremo sui principî che stanno alla base della teoria quantistica, già trattati in un altro articolo di questa opera (v. quanti, teoria dei, vol. V). Ci sembra invece utile ricordare, in quanto costituisce una importante premessa a buona parte della chimica computazionale, che la grande differenza fra la massa degli elettroni e quella dei nuclei ha permesso di formulare un criterio di approssimazione, detto 'approssimazione di Born-Oppenheimer', in base al quale nel calcolo dell'energia molecolare risulta legittimo separare i loro rispettivi moti. In altri termini, poiché l'energia degli elettroni non dipende dalla quantità di moto associata ai moti nucleari, nella trattazione dei moti elettronici si può assumere che i nuclei atomici siano fissi nello spazio. Questa approssimazione è solitamente molto buona, sicché nel suo ambito lo studio della dinamica nucleare può essere agevolmente perseguito valutando l'energia della compagine elettronica per le diverse configurazioni nucleari.
Ciò premesso, si può osservare che l'energia totale di una molecola è costituita da una serie di termini che possono essere elencati come segue: a) energia cinetica di ciascun elettrone; b) energia potenziale elettrostatica, o coulombiana, dovuta all'attrazione fra elettroni e nuclei, alla repulsione mutua fra ciascuna coppia di elettroni e alla repulsione fra ciascuna coppia di nuclei; c) energie dovute ai moti di traslazione, rotazione e vibrazione delle molecole; in virtù della approssimazione di Born-Oppenheimer, questi moti possono essere trattati separatamente e pertanto non verranno esplicitamente considerati.
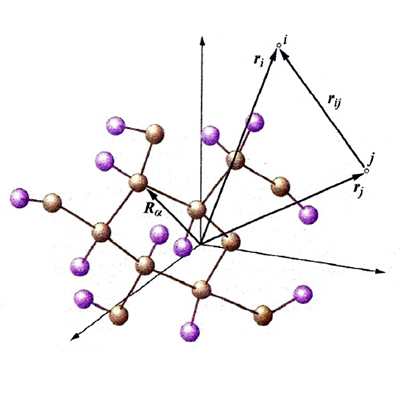
Nel corso del presente articolo ci riferiremo allo schema di fig. 1, nel quale viene mostrato lo scheletro di una molecola, definito dai nuclei atomici α, β, ... (le cui posizioni sono individuate da una serie di vettori Rα), in cui si muovono N elettroni sotto l'azione sia dei campi elettrostatici dei nuclei che di quelli derivanti dalla loro mutua repulsione. Il vettore ri definisce la posizione associata all'elettrone i, mentre il vettore rij, di modulo |ri - rj|, caratterizza la distanza fra gli elettroni i e j. Lo stato di un sistema con N elettroni viene descritto mediante una funzione d'onda Ψ(x) che dipende dalle coordinate x ≡ x1, x2,..., xN associate al moto di ciascuno di essi, tenendo anche conto che gli elettroni si comportano come se girassero su se stessi poiché sono dotati di un momento angolare intrinseco, detto 'momento angolare di spin'. Pertanto le coordinate x includono, oltre alle coordinate spaziali individuate dai vettori r (che sono ovviamente variabili continue), anche le coordinate di spin s, che sono discontinue, potendo assumere solo due valori, compatibilmente con l'orientamento che può avere lo spin sotto l'azione di un campo magnetico. Spesso la Ψ è una funzione complessa che contiene nella sua espressione l'unità immaginaria; pertanto il suo quadrato (più precisamente il suo modulo quadro |Ψ(rN, sN)|2) è dato dal prodotto ΨΨ*, essendo Ψ* la corrispondente funzione complessa e coniugata. La funzione modulo quadro fornisce una distribuzione di probabilità, poiché |Ψ(rN, sN) |2 drN esprime la probabilità di trovare il sistema con coordinate degli elettroni comprese fra rN e rN + drN, e con coordinate di spin uguali a sN. Per un dato sistema esiste una serie di funzioni, ΨG,ΨR,ΨS..., ciascuna corrispondente a uno stato del sistema a partire da quello fondamentale, cioè quello con l'energia più bassa, indicato con G. Tale serie è completa, poiché soddisfa alla seguente condizione (detta di 'ortonormalizzazione'):
formula (1)
essendo dxN = dx1dx2 ... dxN e δRS il simbolo di Kronecker, uguale a 0 se R ≠ S e a 1 se R = S. L'integrazione nella formula (1) è estesa su tutto lo spazio delle coordinate degli elettroni. Dalla funzione d'onda di una determinata molecola è possibile valutare le sue proprietà specifiche, quali la distribuzione della carica elettrica e il valore dell'energia. Purtroppo, già per sistemi contenenti più di due elettroni non si conoscono le espressioni analitiche esatte di tali funzioni d'onda, per cui si deve ricorrere a espressioni ragionevolmente approssimate. In un certo qual senso la storia della ricerca di adeguate funzioni d'onda molecolari si identifica con quella della chimica quantistica computazionale che solo recentemente ha raggiunto risultati soddisfacenti grazie allo sviluppo dei calcolatori elettronici.
Il valore di aspettazione dell'energia, corrispondente al valor medio ottenuto da diverse misurazioni, si valuta dalla funzione d'onda come segue:
formula (2)
dove ℏ indica un operatore differenziale, detto 'hamiltoniano', che agisce sulla funzione d'onda. Nella sua scrittura è opportuno esprimere le grandezze in gioco mediante convenienti unità di misura, dette unità atomiche (a.u.), quali il raggio di Bohr a0 = (h2/4π2me2) = 0,5292 Å, e l'energia di Hartree EH = (4π2e4/h2) = 627,51 kcal/mol, dove e ed m sono rispettivamente la carica e la massa dell'elettrone e h è la costante di Planck. In tale impostazione l'operatore hamiltoniano assume la seguente forma:
formula (3)
essendo ∇i2 = (∂2/∂i2 + ∂2/∂yi2 + ∂2/∂zi2) l'operatore laplaciano associato all'energia cinetica e
il potenziale esterno che agisce sull'elettrone i, dovuto ai nuclei di carica Zα. Infine, è ovviamente necessario addizionare i contributi dovuti alla repulsione coulombiana che si esercita fra i diversi elettroni e fra i diversi nuclei, che dipendono dalle loro distanze rij e Rαβ.
3. Stati e orbitali atomici
L'atomo di idrogeno costituisce un oggetto intrinsecamente simmetrico poiché è formato da un protone e da un elettrone, i quali interagiscono con un potenziale elettrostatico di tipo centrale che dipende solo dalla loro distanza r. Il problema del moto di un elettrone in tale campo di forze è stato affrontato risolvendo in modo esatto la corrispondente equazione di Schrödinger, che permette di ottenere sia i valori delle energie dei diversi stati quantici, sia le espressioni delle corrispondenti funzioni d'onda, o autofunzioni. Esse verranno indicate con la lettera χ e si possono esprimere nella seguente forma generale:
χ(r)Yℓm(ϑ, φ) (4)
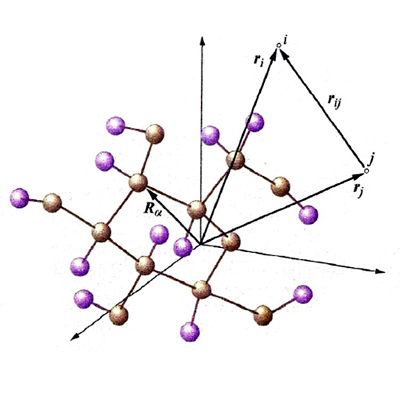
dove Yℓm (ϑ, Φ) sono le funzioni denominate 'armoniche sferiche', ottenute originariamente nell'ambito dello studio delle vibrazioni di una sfera elastica. Esse definiscono la parte angolare delle funzioni d'onda, attraverso gli angoli polari ϑ e φ, mentre la parte radiale R(r) dipende dalla distanza dell'elettrone dal nucleo. Queste funzioni d'onda, dette 'monoelettroniche' poiché dipendono dalle coordinate di un solo elettrone, vengono chiamate 'orbitali atomici'. In corrispondenza dei valori 0, 1, 2, 3, ... del parametro ℓ vengono definiti rispettivamente gli orbitali di tipo s, p, d, f... . Un modo semplice per descriverne la forma è quello di disegnare, come nella fig. 2 per gli orbitali s e p, la zona nella quale la probabilità di trovare l'elettrone è superiore al 95%. Gli orbitali di tipo s hanno simmetria sferica, mentre gli altri sono caratterizzati da lobi che si estendono in particolari direzioni e pertanto in senso figurato descrivono la 'anatomia' dell'atomo di idrogeno.
Per gli atomi con più elettroni è ragionevole assumere che ciascuno di essi si muova indipendentemente dagli altri in un plausibile potenziale di tipo centrale, dovuto all'azione del nucleo, schermato dall'azione media degli altri elettroni. Perciò, si attribuisce agli orbitali un'espressione formalmente uguale alla (4), ma caratterizzata da una diversa funzione radiale. Esistono due tipi di orbitali atomici analitici che meritano di essere menzionati, poiché, come vedremo, vengono impiegati nei calcoli sulle molecole: quelli di Slater (STO, Slater-Type Orbitals) e quelli gaussiani (GTO, Gaussian-Type Orbitals). La forma specifica delle loro corrispondenti funzioni radiali è riportata nella tab. I.
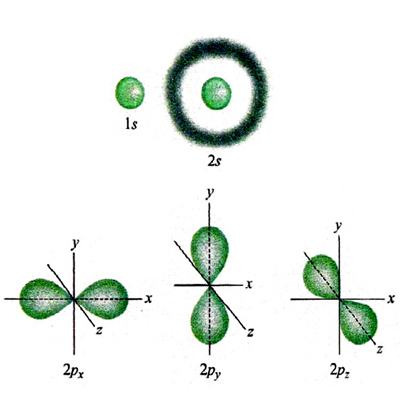
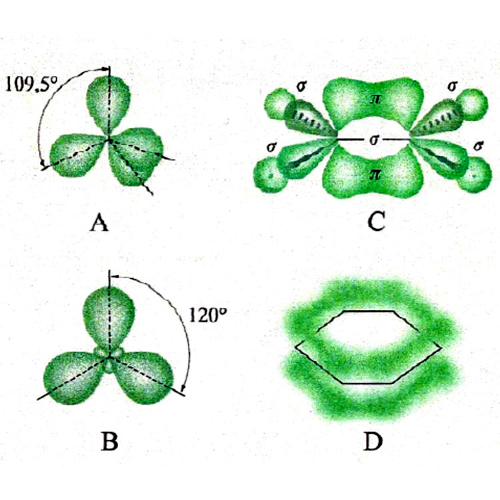
La rottura di simmetria che porta alla complessa morfologia degli orbitali p, d ed f ha una ricaduta significativa sulla struttura delle molecole, poiché i legami fra i diversi atomi tendono a manifestarsi nelle direzioni lungo le quali si riscontra una più elevata sovrapposizione fra i lobi degli orbitali stessi. Si riesce così a giustificare la configurazione geometrica di diverse molecole. Ad esempio, in una molecola d'acqua i due legami O-H formano un angolo di 104,45°, di poco superiore a quello che formano due orbitali p, pari a 90°. La repulsione che si esercita fra i due atomi di idrogeno contribuisce infatti a divaricare l'angolo. In questo quadro risulta di particolare interesse l'atomo di carbonio, nel quale, come ha dimostrato Linus Pauling, l'orbitale 2s e i tre orbitali 2p (questi ultimi aventi la stessa energia) si combinano linearmente formando quattro orbitali, detti ibridi sp3, che partendo dal centro di un tetraedro si dirigono verso i suoi vertici (v. fig. 3A). Questo risultato giustifica la struttura del metano e di tutti i composti della chimica organica alifatica. Sviluppando questa analisi è possibile individuare altre forme di ibridazione che hanno permesso di formulare interessanti modelli concernenti la struttura dei composti insaturi e aromatici della chimica organica. Così, si assume che nella molecola dell'etilene, CH2=CH2, i due atomi di carbonio intervengano mediante tre orbitali ibridi sp2 che puntano verso i vertici di un triangolo equilatero il cui centro è occupato dall'atomo di carbonio stesso. Questi orbitali ibridi (v. fig. 3B) contribuiscono a formare complessivamente cinque legami, denominati 'legami σ', uno fra i due atomi di carbonio e quattro con gli atomi di idrogeno, come illustrato in fig. 3C. I due restanti orbitali p, perpendicolari al piano della molecola e contenenti ciascuno un elettrone, formano un legame (legame π) caratterizzato dal fatto che la massima densità elettronica è concentrata nelle zone al di sopra e al di sotto del piano della molecola. Nella molecola del benzene, C6H6, due dei tre orbitali ibridi sp2 di ciascun atomo di carbonio sono impegnati a formare il suo caratteristico scheletro ciclico esagonale. I sei elettroni π sono invece delocalizzati; essi sono liberi di muoversi in zone anulari che hanno la forma di due ciambelle e che si trovano sopra e sotto il piano della molecola stessa, come illustrato nella fig. 3D. È interessante osservare che questo modello della struttura del benzene è stato successivamente convalidato sperimentalmente mediante la microscopia a scansione a effetto tunnel, come illustrato nella fig. 4.
Questi stupefacenti risultati sembrerebbero dimostrare che le armoniche sferiche costituiscono il 'linguaggio' naturale della chimica, almeno per quanto concerne i suoi aspetti strutturali, quasi a confermare la sorprendente applicabilità della matematica alle scienze naturali evidenziata da Eugene Wigner (v., 1960).
4. Spin-orbitali, antisimmetria e legame chimico
La più comune strategia impiegata per costruire funzioni d'onda polielettroniche che risultino ragionevolmente approssimate è quella di partire da funzioni d'onda monoelettroniche ψk(x) chiamate 'spin-orbitali'. Se si trascura l'interazione fra il moto orbitale e quello di spin esse si possono scrivere come prodotto di due termini:
Ψk (x) = Φk(r)σ(s) (5)
essendo Φk(r) una funzione che dipende unicamente dalle coordinate spaziali dell'elettrone in considerazione, e σ(s) la sua funzione di spin, che solitamente viene indicata con α(s) e β(s) in corrispondenza dell'orientazione verso l'alto o verso il basso che lo spin stesso assume rispetto a un asse opportunamente scelto. La più semplice espressione della funzione d'onda del sistema globale di elettroni è allora la seguente:
Ψ = Ψ1(x1)Ψ2(x2)...ΨN(xN) (6)
in base alla quale a ciascun elettrone viene attribuita una propria funzione d'onda e una propria energia. Questa fruttuosa idea, introdotta da Douglas R. Hartree nello studio degli atomi, riconduce un problema a molti corpi a quello di un insieme di singole particelle in un campo di forze medio definito dalle altre. Tuttavia, l'espressione precedente non soddisfa il principio di Pauli, in base al quale la funzione d'onda di un sistema di elettroni deve essere antisimmetrica, ovvero cambiare di segno quando si scambiano le coordinate di due elettroni:
Ψ (x1, x2,...) = - Ψ (x2, x1...). (7)
Si può dimostrare che questa relazione è compatibile con il fatto che ciascun spin-orbitale può ospitare un solo elettrone, poiché se dovesse essere condiviso da due elettroni essi si respingerebbero. Per questa ragione il principio di Pauli viene anche chiamato 'principio di esclusione'. Questa diminuzione della probabilità di trovare due elettroni aventi lo stesso spin in prossimità uno dell'altro si può anche descrivere attribuendo a ciascuno di essi uno spazio 'privato' chiamato 'cavità di Fermi'.
Un semplice accorgimento matematico per costruire una funzione d'onda antisimmetrica consiste nell'utilizzare un determinante, detto 'determinante di Slater', avente la seguente forma:
formula (8)
dove ciascuna riga si riferisce a un particolare elettrone che occupa uno degli N spin-orbitali. È facile osservare che lo scambio di due righe del determinante, corrispondente allo scambio di due elettroni, cambia anche il segno del determinante stesso.
La ricaduta del principio di esclusione sull'energetica atomica e molecolare è profonda e significativa. Per illustrare questo aspetto soffermiamo l'attenzione sul primo stato eccitato dell'atomo di elio con i suoi due elettroni negli stati 1s e 2s, entrambi a simmetria sferica. Se si trascura l'interazione fra il moto orbitale e quello di spin, si può procedere esprimendo la funzione d'onda globale come prodotto di una funzione delle sole coordinate spaziali e di una funzione delle coordinate di spin. Per la prima di esse si devono considerare due stati aventi la stessa energia, detti 'degeneri', derivanti da uno scambio degli elettroni fra i due orbitali atomici in gioco. Ignorando per semplicità la presenza di un fattore di normalizzazione, irrilevante per la nostra analisi, le corrispondenti funzioni d'onda si possono scrivere come segue:
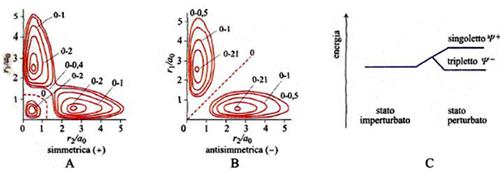
Ψ±(1,2) ∝ 1s(1)2s(2) ± 1s(2)2s(1) (9)
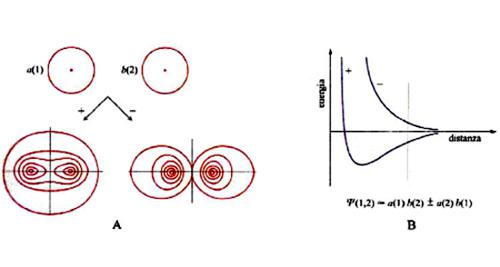
dove la funzione con il segno + è simmetrica e quella con il segno - è antisimmetrica. È ora interessante osservare che se si riportano su un diagramma i contorni delle probabilità di trovare i due elettroni a una determinata distanza dal nucleo si ottengono le situazioni illustrate nella fig. 5, A e B. Per la combinazione antisimmetrica la probabilità di trovare entrambi gli elettroni alla stessa distanza dal nucleo, ovvero sulla diagonale, è nulla, mentre viceversa per la combinazione simmetrica essa è molto elevata. Per completare l'analisi è ora necessario tenere conto che gli elettroni con spin orientati in senso diverso, ovvero antiparallelo, risultano descritti da un'unica funzione antisimmetrica rispetto allo scambio dello spin (stato 'di singoletto'). Se viceversa gli spin sono orientati nello stesso senso, ovvero sono paralleli, il loro stato risulta descritto da tre funzioni degeneri antisimmetriche (stato 'di tripletto'). In virtù del principio di Pauli l'autofunzione globale deve risultare antisimmetrica per cui lo stato di singoletto deve essere associato alla Ψ+ che, come illustrato nella fig. 5A, è compatibile con l'esistenza di una zona nella quale è elevata la probabilità di trovare entrambi gli elettroni. Ne deriva allora che lo stato risulta meno stabile (a più alta energia) per la presenza della elevata repulsione elettrostatica. Questa tipica interazione, detta 'di scambio' o più modernamente di 'correlazione di spin', costituisce un effetto della meccanica quantistica, non interpretabile in base a una descrizione classica. Se si applicano i concetti precedenti al sistema bielettronico della molecola di idrogeno, emerge la situazione illustrata nella fig. 6. Anche in questo caso si ottengono due stati elettronici degeneri, uno con gli elettroni antiparalleli (singoletto) e uno con gli elettroni paralleli (tripletto). Nel primo di essi la coppia di elettroni è sostanzialmente localizzata nella regione compresa fra i due protoni e pertanto scherma la loro repulsione elettrostatica. Essa si comporta quindi come una 'colla' e contribuisce alla formazione di un legame. Questo aspetto è stato descritto per la prima volta nel 1927 in un famoso lavoro di Walter Heitler e Fritz London che è considerato attualmente una pietra miliare nella teoria del legame chimico. Il risultato ottenuto evidenzia il ruolo esercitato dalle coppie elettroniche nella formazione dei legami chimici, preconizzato da Gilbert N. Lewis prima dell'avvento della meccanica quantistica.
5. Il modello di Hartree-Fock del campo autocompatibile
Per sviluppare metodi quantitativi soddisfacenti per il calcolo dell'energia delle molecole è stato necessario risolvere diversi problemi. Il procedimento applicato è quello degli orbitali molecolari autocompatibili mutuato dai lavori condotti sugli atomi da Hartree e da Vladimir A. Fock, in cui il moto di ciascun elettrone di una molecola viene descritto mediante funzioni d'onda monoelettroniche chiamate 'orbitali molecolari'. Inoltre, si trascurano le interazioni fra i moti orbitali e quelli di spin, per cui si esprimono gli spin-orbitali mediante la relazione (5). Riferiamoci anzitutto al caso speciale, ma rilevante, di una molecola con un numero pari di elettroni e, pertanto, dotata di una configurazione, detta 'a guscio chiuso', nella quale ciascun orbitale ϕk è occupato da due elettroni con spin α e β, rispettivamente. In questo caso, gli N spin-orbitali si possono suddividere in N/2 orbitali della forma ϕk(r)α(s) e N/2 della forma ϕk(r)β(s). Il calcolo dell'energia può essere eseguito mediante la formula (2), utilizzando il corrispondente determinante di Slater (8) per esprimere opportunamente la funzione d'onda antisimmetrizzata (v. legame chimico, vol. III). Si ricava la seguente espressione:
formula (10)
dove la somma è estesa sugli N/2 orbitali occupati da due elettroni. Hk viene chiamata 'energia di core' dell'elettrone descritto dall'orbitale ϕk ed è data dalla somma della sua energia cinetica e di quella di interazione elettrostatica con i nuclei. Jkl rappresenta invece l'energia di repulsione elettrostatica fra gli elettroni descritti dagli orbitali ϕk e ϕℓ. Ciascuno di essi è infatti soggetto all'azione di un potenziale dovuto in parte ai nuclei e in parte al campo generato dagli elettroni presenti negli altri orbitali. Il campo prodotto dall'elettrone nell'orbitale ϕk viene espresso mediante una distribuzione di carica uniforme avente densità uguale a -ϕk*ϕk = - |ϕk (r)|2, come illustrato nella fig. 7. In sostanza, l'interazione fra gli N elettroni viene espressa mediante un campo medio che differisce da quello reale per l'assenza di un termine fluttuante. Più sottile è il significato del termine Kkℓ, detto 'di scambio', la cui presenza è dovuta specificamente all'impiego del determinante di Slater invece del semplice prodotto degli orbitali. La sua influenza sull'energia si manifesta nel modo che è stato precedentemente illustrato per l'atomo di elio e per la molecola di idrogeno.
Solitamente gli orbitali molecolari vengono espressi mediante una combinazione lineare degli orbitali atomici (approssimazione LCAO, Linear Combination of Atomic Orbitals):
formula (11)
La precedente relazione trova una giustificazione nel fatto che l'elettrone in prossimità di ciascun nucleo risulta essenzialmente soggetto al suo campo di forza e pertanto il suo comportamento è descritto dal corrispondente orbitale atomico.
La ricerca della migliore serie dei coefficienti ckp viene perseguita applicando il principio variazionale, in base al quale i valori delle energie corrispondenti a funzioni d'onda approssimate, quali quelle espresse dalla (11), sono superiori, o al limite uguali, all'energia E0 dello stato fondamentale del sistema. Questo problema è stato affrontato e risolto nel 1951 da Clemens C. J. Roothaan, il quale ha dimostrato che la ricerca del valore minimo dell'energia, sotto il vincolo che le funzioni d'onda siano ortonormali e quindi soddisfino alla relazione (1), porta al seguente sistema di equazioni algebriche simultanee:
formula (12)
dove:
formula (13)
Le espressioni specifiche e il significato dei termini presenti nelle equazioni precedenti sono riassunti in tab. II, mentre i valori che assumono i parametri ε, noti come 'energie degli orbitali', forniscono una valutazione approssimata del potenziale di ionizzazione, ovvero dell'energia richiesta per strappare il corrispondente elettrone dalla molecola e portarlo a una distanza infinita. Una soluzione non banale del sistema (12) impone che sia soddisfatta la condizione:
∣ Fpq − εSpq ∣ = 0 (14)
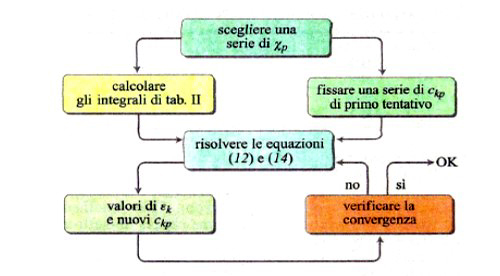
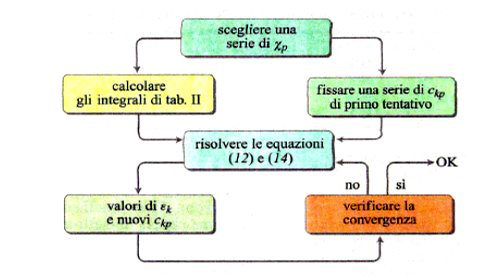
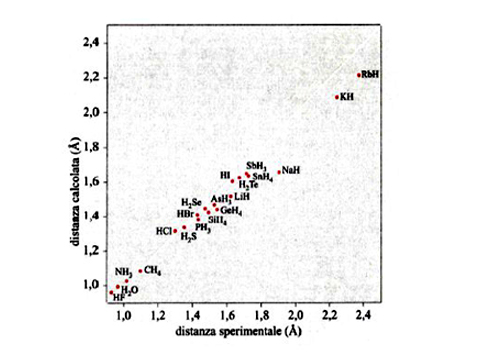
Lo sviluppo del determinante (14) porta a un'equazione algebrica avente come incognita ε, di grado uguale al numero di orbitali atomici coinvolti nella (11). Il sistema di equazioni non lineari (12) viene solitamente risolto per via numerica mediante il procedimento iterativo illustrato in fig. 8. Tale metodo, indicato con l'acronimo LCAO-SCF (Linear Combination of Atomic Orbitals Self-Consistent Field), è stato esteso anche ai sistemi a guscio aperto, nei quali, cioè, alcuni orbitali sono occupati da un solo elettrone anziché da due. In tal modo il metodo può essere applicato anche alle specie chimiche contenenti un elettrone spaiato. L'insieme degli orbitali atomici impiegati χp (r, ϑ, φ), centrati su ciascun nucleo atomico, viene chiamato 'serie di funzioni di base' (basis set), e i calcoli così eseguiti vengono denominati ab initio. Essi venivano inizialmente condotti utilizzando quali orbitali atomici gli orbitali di Slater, che però implicano elevate difficoltà nella soluzione degli integrali della tab. II, soprattutto quando gli orbitali atomici in gioco sono centrati su tre o quattro atomi. Ciò ha dato luogo a un rallentamento del 'programma' della chimica quantistica, creando fra i ricercatori un clima di sconforto derivante "dall'incubo degli integrali" (v. Pople, 1999). La situazione si è protratta per alcuni anni, sino a quando ha cominciato ad affermarsi un suggerimento di Frank Boys, che propose di utilizzare orbitali atomici gaussiani, mediante i quali il calcolo degli integrali risulta molto più agevole e perseguibile per via analitica. Questo approccio, che è maturato negli ultimi vent'anni grazie allo sviluppo del calcolo elettronico, ha permesso di formulare programmi sofisticati grazie ai quali è ormai possibile, in certi casi, eseguire una valutazione dell'energia molecolare con una approssimazione dell'1%. In queste procedure di calcolo, il comportamento degli elettroni di ciascun atomo viene descritto mediante una serie di funzioni di base le cui caratteristiche sono riassunte nella tab. III. In particolare, per gli elettroni coinvolti nei legami si impiegano combinazioni di funzioni gaussiane che permettono maggiore flessibilità nella descrizione del loro comportamento. Per rendersi conto dell'impegno di calcolo numerico richiesto, è sufficiente osservare che il numero degli integrali di interazione elettronica coinvolti è all'incirca proporzionale a N4, dove N è il numero di funzioni atomiche impiegate. Il metodo è sufficientemente accurato per calcolare le configurazioni geometriche delle molecole ricercando il minimo della loro energia in funzione delle distanze e degli angoli di legame. A titolo di esempio, nella fig. 9 viene riportato il confronto fra i valori sperimentali e quelli calcolati delle distanze di legame di diversi idruri.
6. Ruolo della correlazione elettronica
Il metodo del campo autocompatibile, pur fornendo valori accurati dell'energia molecolare totale, soffre di un grave inconveniente derivante dall'impiego di funzioni d'onda monoelettroniche. In tale impostazione, infatti, il moto di ciascun elettrone viene influenzato da quello degli altri solo attraverso un campo medio, ignorando il fatto che la repulsione elettrostatica istantanea dà origine a una 'correlazione' nel moto di ciascuna coppia di elettroni che si riflette sulla probabilità di trovarli a una specifica distanza reciproca. Infatti, per effetto della repulsione elettrostatica, esiste una probabilità ridotta di trovare un elettrone in prossimità di un altro. Questo effetto viene anche attribuito alla presenza di una 'cavità (o buca) di Coulomb' che in realtà non può essere disgiunta da quella di Fermi precedentemente introdotta. Pertanto, in termini più generali ci si riferisce a una 'cavità di scambio-correlazione', con dimensioni tipiche dell'ordine dell'Ångstrom. Tale fenomeno contribuisce all'energia associata a una coppia di elettroni di un legame per circa 25 kcal/mole, quindi per un valore dello stesso ordine di grandezza delle energie di legame (v. Raghavachari e Anderson, 1996). L'energia totale di una molecola viene riferita a quella delle particelle separate, ovvero i nuclei e gli elettroni. L'energia di un atomo è la somma di tutti i potenziali di ionizzazione; nel passaggio a una molecola si deve aggiungere il contributo delle energie di legame e di quelle di punto zero associate a ciascun moto vibrazionale. Ad esempio per l'acqua il valore sperimentale dell'energia, una volta sottratta quella relativistica (stimata - 0,045 a.u.), ammonta a - 76,438 ± 0,003 a.u., di cui - 0,370 a.u. (232,18 kcal/mole) corrispondono all'energia di correlazione. In realtà, il valore totale dell'energia è spesso irrilevante poiché interessano soprattutto le sue variazioni. Se si 'stira' un legame tale variazione è associata soprattutto all'energia di correlazione della coppia di elettroni coinvolti nel legame. Se si trascura tale energia, perciò, si commettono errori molto elevati nel calcolo delle energie di dissociazione. Questo fatto ha conseguenze catastrofiche nella modellazione dei processi di rottura e formazione dei legami che intervengono durante le reazioni chimiche. Si tratta di una difficoltà che era stata efficacemente evidenziata da Robert Mulliken, premio Nobel per la chimica nel 1966, mediante una laconica affermazione: "l'energia di legame è una noce dura da rompere".
L'energia di correlazione è definita come la differenza fra il valore sperimentale dell'energia, depauperato dagli effetti relativistici (spesso trascurabili), e quello ottenuto dalla soluzione esatta delle equazioni del campo autocompatibile. Essa rappresenta uno 'spiacevole inconveniente', poiché il suo calcolo non risulta agevole. L'approccio più generale, dovuto a Christian Moller e Milton S. Plesset, si riconduce a un'applicazione del metodo delle perturbazioni, in base al quale l'hamiltoniana esatta Ĥ viene espressa in funzione di un parametro λ nel modo seguente:
formula (15)
essendo F l'hamiltoniana del corrispondente modello di Hartree-Fock cui compete l'autofunzione Ψ0 e al quale si ricade se λ = 0, mentre se λ = 1 si ottiene l'hamiltoniana esatta. Se si esprime a sua volta l'autofunzione come sviluppo in serie nel parametro λ:
Ψ = Ψ0 + λΨ1 + λ2Ψ2 + λ3Ψ3 + ... (16)
si ricava un corrispondente sviluppo per l'energia:
E = E0 + λE1 + λ2E1 + λ3E3 +... (17)
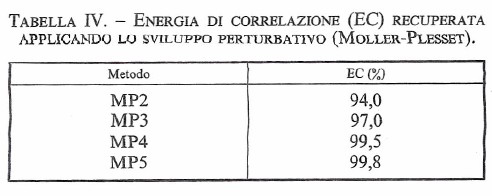
La serie viene troncata al termine desiderato e successivamente si attribuisce a λ un valore unitario. L'energia E0 è identica al valore di Hartree-Fock , mentre E1, E2, ..., si riferiscono ai diversi ordini del calcolo perturbativo (che viene indicato con le sigle MP2, MP3, ecc., a seconda del numero di termini considerati). L'approccio è corretto ma purtroppo la serie così ottenuta è lentamente convergente e presenta nel suo sviluppo espressioni algebriche sempre più complesse. Comunque, la sua applicazione permette di recuperare i valori dell'energia di correlazione, con una efficacia che dipende ovviamente dall'ordine cui si spinge lo sviluppo (17), come illustrato nella tab. IV.
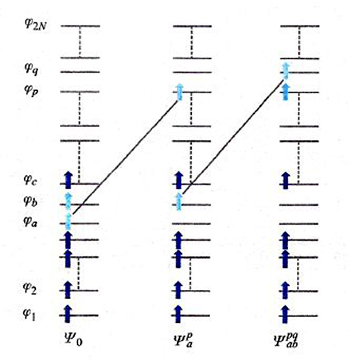
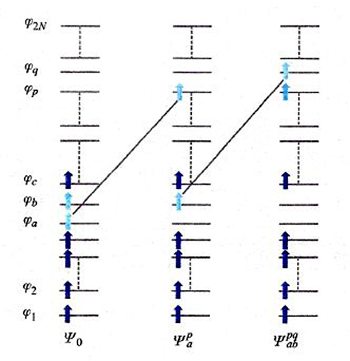
Un diverso approccio al calcolo dell'energia di correlazione, detto 'metodo della interazione fra configurazioni', procede esprimendo le funzioni d'onda dello stato fondamentale e degli stati eccitati attraverso una combinazione lineare di tutti i possibili, e quindi potenzialmente infiniti, determinanti di Slater con N elettroni, ottenuti mediante la promozione di 1, 2, 3, ... elettroni dagli orbitali occupati nello stato fondamentale a orbitali eccitati, anche virtuali. Come esemplificato nello schema di fig. 10, la funzione d'onda viene espressa nel modo seguente:
formula (18)
I coefficienti dello sviluppo vengono valutati applicando il principio variazionale. Purtroppo, lo sviluppo converge molto lentamente, e quindi, per ragioni pratiche, esso deve essere troncato, talora anche arbitrariamente, ai primi termini, rendendo l'applicazione del metodo onerosa e non sempre efficace. Il suo impiego risulta però necessario se si studiano transizioni elettroniche a stati molecolari eccitati.
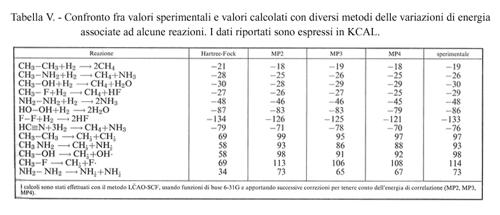
In conclusione, con il metodo LCAO-SCF, includendo l'effetto della correlazione elettronica, si ottengono valori sufficientemente accurati tanto delle energie molecolari, dai quali si risale alle configurazioni geometriche delle molecole, quanto delle variazioni di energia associate a reazioni chimiche, cioè della differenza fra i valori delle energie che competono rispettivamente ai prodotti di reazione e ai reagenti. A titolo di esempio, in tab. V viene riportato un confronto fra dati sperimentali e valori calcolati, con diverse approssimazioni, delle variazioni di energia associate a una serie di reazioni chimiche.
Per descrivere i moti di vibrazione delle molecole, che in prima approssimazione si possono assumere armonici, è necessario espandere in serie di Taylor l'energia in funzione delle coordinate nucleari nell'intorno della configurazione di equilibrio. Ad esempio, per una molecola biatomica, i cui atomi hanno masse m1 ed m2, si scrive:
formula (19)
essendo R0 il valore della distanza di equilibrio. Il primo termine al secondo membro può essere posto convenzionalmente uguale a zero, mentre il secondo termine è nullo poiché la derivata è calcolata in corrispondenza del punto di equilibrio. Pertanto, approssimativamente si può scrivere:
formula (20)
avendo introdotto la costante di forza elastica k, dalla quale si può calcolare la frequenza di vibrazione attraverso la nota relazione:
formula (21)
dove μ = m1m2/(m1 + m2) è la massa ridotta della molecola. È importante ricordare che a ciascuna vibrazione è associata un'energia, detta 'energia di punto zero', uguale a (1/2)hν e corrispondente al più basso livello energetico. Dalla conoscenza delle energie molecolari e delle frequenze di vibrazione si può procedere al calcolo delle funzioni di stato termodinamiche, quali l'entalpia, l'entropia e l'energia libera (v. termodinamica molecolare, vol. XI).
7. Metodi semiempirici
L'applicazione del metodo LCAO-SCF a molecole complesse risulta piuttosto onerosa. Ciò ha favorito la formulazione di alcune sue versioni approssimate, dovute in gran parte agli sforzi di Pople, Robert Parr, Michael S. Dewar e dei loro collaboratori. Una tecnica comunemente utilizzata consiste nell'ignorare gli elettroni interni degli atomi tenendo conto soltanto di quelli che partecipano alla formazione dei legami. Pertanto, i termini che esprimono l'energia cinetica e di attrazione nucleare sono riferiti a un core efficace che definisce uno pseudopotenziale. Inoltre, si introducono alcune semplificazioni nel calcolo delle interazioni fra gli elettroni basate sull'impiego di parametri determinati da dati sperimentali, quali le energie di formazione di molecole di riferimento o da quelle associate ad alcune transizioni elettroniche. La semplificazione più drastica, chiamata ZDO (Zero Differential Overlap), consiste nell'attribuire un valore nullo al prodotto di due orbitali atomici diversi anche se occupati dallo stesso elettrone, ovvero nel porre χ*p(r)χq(r) = 0 se p ≠ q. Ne consegue immediatamente che gli integrali di sovrapposizione di tab. II risultano uguali a 1 se condotti sullo stesso orbitale e uguali a 0 in tutti gli altri casi. Ancora più importante è la ricaduta sugli integrali di interazione elettronica il cui calcolo, se sono coinvolti tre o quattro centri atomici, risulta molto oneroso. Se si impiega la notazione di tab. II e si introduce la ZDO, in un sol colpo si ottiene:
< pqrs >=δpqδ rs < pprr > (22)
eliminando così gli integrali su tre o quattro centri.
Un'ampia applicazione dell'approssimazione precedente è stata effettuata sui sistemi di elettroni π presenti nelle molecole con doppi legami coniugati, per esempio il benzene e gli idrocarburi poliaromatici quali il naftalene e il fenantrene, ottenuti dalla condensazione di diverse molecole di benzene. Questa procedura è nota come 'metodo di Pariser-Parr-Pople' (PPP) e i suoi principali successi sono stati ottenuti nella descrizione degli spettri elettronici, nel calcolo della densità di carica degli elettroni π (e quindi dei momenti dipolari) e nella valutazione dei potenziali di ionizzazione.
In realtà, poiché i sistemi di elettroni π sono comuni nella chimica organica non soltanto negli idrocarburi aromatici ma anche in quelli polietilenici e nei nuclei aromatici contenenti eteroatomi, quali la piridina e altri, essi hanno costituito in un certo senso la 'palestra' per l'applicazione della meccanica quantistica alla chimica. Il primo dei metodi proposti è dovuto a Erich Hückel e, pur risalendo al 1929, viene tuttora impiegato per la sua semplicità ed efficacia, sia pure nei limiti imposti dalle sue approssimazioni. In questo metodo la funzione d'onda del sistema di elettroni π viene espressa mediante la relazione (6), ovvero come prodotto di orbitali molecolari ottenuti come combinazione degli orbitali atomici di tipo p. Inoltre, il moto di ciascun elettrone viene riferito a una hamiltoniana efficace Ĥ che mediamente comprende le interazioni sia con i nuclei che con gli altri elettroni. In questa impostazione, l'energia dipende da due tipi di integrali, chiamati rispettivamente 'integrale coulombiano', uguale a ∫χp(r)Ĥeχp(r)dr, e 'integrale di scambio', con p adiacente a q, dato da ∫χp(r)Ĥeχq(r)dr, che in pratica vengono trattati quali parametri empirici. Negli integrali precedenti si è posto per semplicità drN ≡ dr = dx1 dx2... Un problema interessante riguarda la stabilità delle molecole contenenti doppi legami che possono dare origine a sistemi di elettroni π. Essa può essere valutata calcolando la differenza fra l'energia della molecola in cui ciascun elettrone π appartiene all'atomo di origine e quella della molecola in cui tali elettroni sono delocalizzati. Se il valore così ottenuto è positivo, la molecola è stabile e viene classificata come 'aromatica' (v. Aihara, 1992). È stato così possibile ricavare una semplice regola in base alla quale un composto ciclico insaturo risulta particolarmente stabile quando il numero di elettroni delocalizzati è uguale a (4n + 2) con n = 1, 2, 3, ... . In sostanza, esiste una successione di numeri 'magici' che corrispondono al numero di elettroni richiesti per riempire dei gusci molecolari. Con n = 1 si ottiene il benzene, il cui sestetto di elettroni corrisponde a uno strato chiuso analogo a quello degli elettroni dei gas nobili. In fig. 11 sono riportati i risultati dei calcoli dell'energia degli elettroni π per alcune molecole cicliche insature. Fra di esse è presente una molecola curiosa, costituita unicamente da 60 atomi di carbonio connessi fra di loro in una compagine di 20 anelli esagonali e 12 anelli pentagonali: il 'buckminsterfullerene', dal nome dell'architetto che ha progettato delle cupole aventi tale struttura (v. anche fullereni, vol. XII).
8. Metodo del funzionale della densità
In due lavori pionieristici, pubblicati indipendentemente nel 1927, Enrico Fermi e Llewellyn H. Thomas hanno dimostrato come fosse possibile ottenere attraverso un approccio statistico una descrizione ragionevolmente approssimata della distribuzione degli elettroni in un atomo polielettronico, evidenziando che la funzione d'onda poteva essere sostituita dalla densità elettronica ρ(r), grandezza più semplice e sperimentalmente misurabile. Essa esprime il numero di elettroni presenti nell'unità di volume e soddisfa la relazione:
N = ∫ ρ (r)dr (23)
essendo al solito dr un elemento di volume.
Sfortunatamente tale impostazione non si rivelò applicabile alle molecole, poiché non permetteva di prevedere la formazione dei legami. La situazione cambiò però nel 1964 quando, grazie a un lavoro di Pierre Hohenberg e Walter Kohn, risultò che il modello di Thomas-Fermi costituisce in realtà solo un'approssimazione di una teoria esatta nella quale la densità elettronica gioca un ruolo di primo piano.
Prima di procedere è opportuno ricordare che, così come una funzione si può considerare come una 'prescrizione' per produrre un numero a partire da una serie di variabili, similmente un funzionale si può considerare come una 'prescrizione' per produrre un numero da una funzione che a sua volta dipende da più variabili. La Ψ(r) e la ρ(r) sono entrambe funzioni, mentre l'energia, che dipende dalla funzione d'onda, è un funzionale. Per evidenziare tale caratteristica, essa viene scritta nella forma E[Ψ(r)], caratterizzando il funzionale con le parentesi quadre. Ciò premesso, è interessante osservare che se accettiamo l'approssimazione di Hartree (6), l'energia degli elettroni di un atomo o di una molecola può essere espressa mediante la densità ρ(r) come segue:
formula (24)
essendo T[ρ(r)] l'energia cinetica e υ(r) quella potenziale di interazione con i nuclei. L'energia potenziale compare come somma di due interazioni elettrostatiche classiche, la prima fra elettroni e nuclei, la seconda fra le due distribuzioni elettroniche ρ(r) e ρ(r′). Avendo assunta valida l'approssimazione di Hartree, l'interazione di scambio è assente, così come l'interazione istantanea diretta elettrone-elettrone che dà origine all'energia di correlazione.
Nell'ambito dell'approssimazione di Thomas-Fermi si dimostra che l'energia cinetica si può valutare mediante la relazione:
TTF [ρ(r)] = 2,8712 ∫ ρ5/3 (r)dr (25)
Infatti, se a un generico elettrone situato in una posizione definita da r e avente quantità di moto p(r) si associa una cavità di Fermi sferica di diametro a(r), la densità locale risulta espressa da ρ(r) = [1/6πa3(r)]. Poiché, in virtù del principio di indeterminazione, p ≈ h/a, l'energia cinetica locale dell'elettrone sarà espressa da ε(r) = (1/2m) p2 (r) ∝ (h2/m)ρ2/3(r). L'energia cinetica totale si calcolerà allora integrando l'espressione ε(r)ρ(r)dr, e quindi mediante la (25). Purtroppo, però, questa espressione non risulta sufficientemente accurata per affrontare problemi di energetica molecolare.
Hohenberg e Kohn, nel lavoro menzionato, hanno dimostrato che l'energia dello stato fondamentale di un sistema di elettroni è un funzionale della densità elettronica che in forma esatta si può scrivere come segue:
formula (26)
Il termine NC[ρ(r)], che può essere definito 'non classico' poiché contiene l'energia di scambio e di correlazione, risulta implicitamente definito dalla (26) stessa. Questo importante risultato ha aperto il problema di trovare un opportuno funzionale che permetta di valutare i diversi termini presenti in questa equazione. Si tratta di un approccio che ha portato alla formulazione di un metodo, chiamato 'teoria del funzionale della densità' (DFT, Density Functional Theory), che si può considerare una vera e propria innovazione nel panorama dell'energetica molecolare (v. Kohn e altri, 1996; v. Parr e Yang, 1989). Un efficace procedimento, suggerito dallo stesso Kohn e da Lu J. Sham, è basato sull'impiego di un determinante di Slater costruito su una serie di opportuni orbitali molecolari ῳk(r) relativi a un sistema di elettroni non interagenti, mediante i quali si può esprimere la densità elettronica nel modo seguente:
formula (27)
Si dimostra che utilizzando tali orbitali l'energia si può esprimere come somma dell'energia cinetica esatta degli elettroni non interagenti e dell'energia dovuta a un potenziale efficace avente la seguente forma:
formula (28)
dove
formula (29)
è la derivata funzionale di un opportuno termine Exc[ρ(r)], essendo δ(r-r′) la funzione di Dirac. Questo termine contiene l'energia di scambio e di correlazione, e inoltre una piccola correzione dovuta all'influenza della correlazione stessa sull'energia cinetica. Applicando il principio variazionale all'espressione dell'energia così ottenuta, sotto il vincolo della (23) si ricava la seguente serie di equazioni:
formula (30)
che può essere risolta per via numerica con un procedimento iterativo. Quindi, sotto questo aspetto il metodo DFT richiama quello LCAO-SCF, anche se la sua applicazione risulta più agevole e per certi versi più efficace. Si ricava così la serie dei migliori orbitali ϕk, e i corrispondenti valori delle εk, che in questo caso non hanno però un significato fisico preciso. Il metodo esposto è esatto, ma purtroppo la valutazione della Exc[ρ(r)] richiede l'impiego di opportune assunzioni e approssimazioni, sostanzialmente basate sul fatto che, come abbiamo visto, gli effetti di scambio e di correlazione riflettono un'azione di schermatura poiché ciascun elettrone tende a escludere che gli altri gli si avvicinino. L'energia di correlazione viene scritta come somma di due contributi relativi, rispettivamente, allo scambio e alla correlazione:
Exc[ρ(r)] = Ex[ρ(r)] + Ec[ρ(r)]. (31)
Sfortunatamente un calcolo esatto di questi termini risulta di elevata difficoltà. Tuttavia, per il termine di scambio è stata individuata un'approssimazione molto semplice, ma sorprendentemente utile, chiamata 'approssimazione della densità locale' (LDA, Local Density Approximation). Essa fruisce dei risultati ottenuti nello studio del comportamento di un gas elettronico distribuito in modo uniforme in una scatola nella quale è presente un potenziale positivo e omogeneo tale da mantenere il sistema neutro. In questo caso si dimostra che:
ELDAx[ρ] = −0,7386 ∫[ρα4/3 + ρβ4/3]dr (32)
essendo ρα e ρβ i contributi alla densità dovuti agli elettroni rispettivamente con spin α e β. Ovviamente ρα + ρβ = ρ, mentre nei sistemi a strato chiuso ρα = ρβ. Non esistono invece espressioni analitiche del contributo di correlazione ELDA, per cui la sua valutazione è stata condotta con metodi numerici, ad esempio utilizzando la tecnica Monte Carlo. I risultati ottenuti sono stati successivamente interpolati in modo da poterli agevolmente impiegare nelle diverse applicazioni.
Malgrado la semplicità delle ipotesi che stanno alla sua base, l'approssimazione LDA fornisce risultati di soddisfacente accuratezza. Si può comunque migliorare la valutazione del termine di scambio tenendo conto che la densità elettronica non è omogenea e introducendo quindi un'opportuna correzione, detta di 'non località' (LDANL), che dipende ad esempio dal seguente fattore di scala adimensionale:
formula (33)
Un procedimento analogo è stato impiegato per valutare con maggior cura anche l'energia di correlazione.
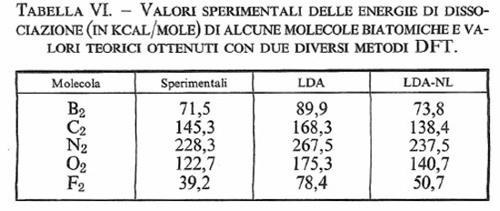
Esistono diverse varianti del metodo DFT che differiscono soprattutto per la scelta delle funzioni atomiche di base. In generale, si è riscontrato che i risultati ottenuti nel calcolo della geometria e delle frequenze di vibrazione delle molecole sono confrontabili con quelli ricavati con il metodo LCAO-MO-SCF. Nella tab. VI vengono confrontati i valori delle energie di legame di alcune molecole biatomiche valutati con i metodi LDA e LDA-NL.
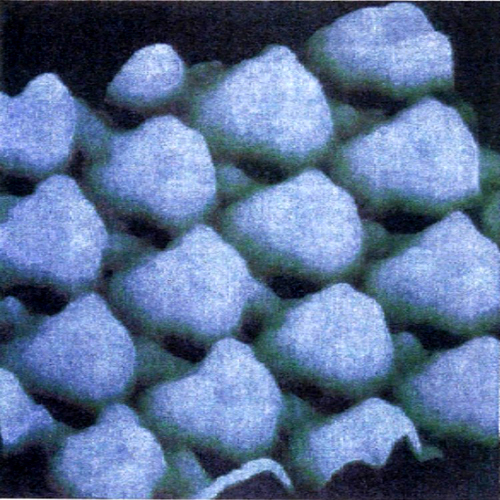
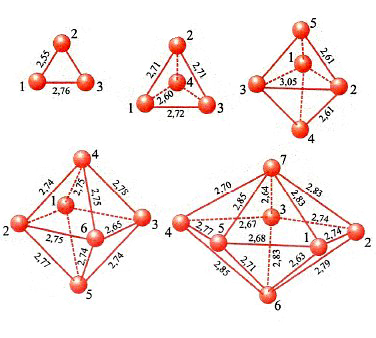
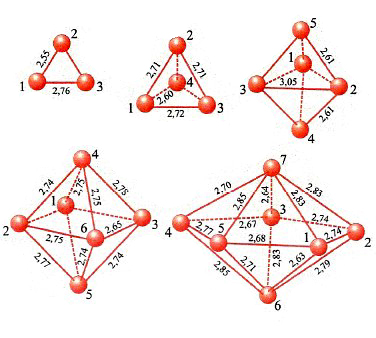
In conclusione, il metodo DFT costituisce attualmente un utile strumento per valutare le caratteristiche strutturali e, come vedremo, dinamiche delle molecole. La sua applicazione permette anche di esplorare il comportamento di strutture molecolari di particolare interesse, quali le nanostrutture. A titolo di esempio in fig. 12 vengono illustrate le strutture ottenute per clusters di palladio le cui caratteristiche si rivelano di interesse per approfondire alcuni aspetti della catalisi eterogenea (v. Bertani e altri, 2000 e 2001).
9. Cinetica e dinamica delle reazioni chimiche
La velocità di una trasformazione chimica dipende dalla frequenza degli incontri fra le molecole reagenti, che a sua volta è proporzionale al prodotto delle loro concentrazioni. In un lavoro fondamentale che risale al 1889, Svante Arrhenius mise in evidenza che il fattore di proporzionalità, chiamato 'costante di velocità di reazione' k(T), si può esprimere con ragionevole approssimazione attraverso la relazione:
k(T) = Ae−Ea/RgT (34)
dove Rg è la costante dei gas, T la temperatura e A ed Ea sono grandezze caratteristiche chiamate rispettivamente 'fattore di frequenza' ed 'energia di attivazione'.
Molto spesso le trasformazioni chimiche coinvolgono diversi stadi elementari nei quali intervengono composti instabili e reattivi che, se pure presenti in piccola quantità, possono influenzare in modo significativo la velocità del processo globale. Rientrano in questa tipologia le reazioni di combustione, le trasformazioni chimiche che hanno luogo nell'atmosfera, i processi enzimatici e molti altri. Per poter formulare opportuni modelli in grado di descrivere sia i processi naturali che quelli di interesse applicativo, è necessario conoscere i parametri che caratterizzano le velocità delle reazioni in essi coinvolte. Poiché la loro determinazione per via sperimentale non è sempre agevole, risulta utile poter disporre di metodi di calcolo in grado di sopperire a tale esigenza.
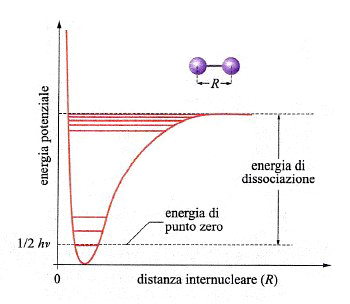
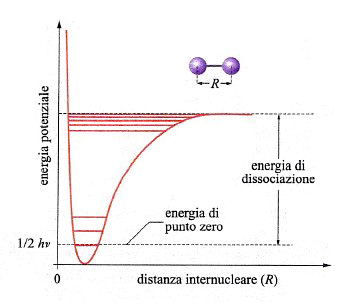
Una reazione chimica avviene attraverso la rottura e la formazione di legami fra atomi. In una molecola biatomica la distanza di legame corrisponde al valore minimo di una curva di energia potenziale che ha il tipico andamento illustrato nella fig. 13. In realtà, l'energia è quantizzata e può assumere solo una serie di valori discontinui, il più basso dei quali è quello di punto zero, pari a (1/2)hν, un valore superiore a quello del minimo della curva di energia potenziale.
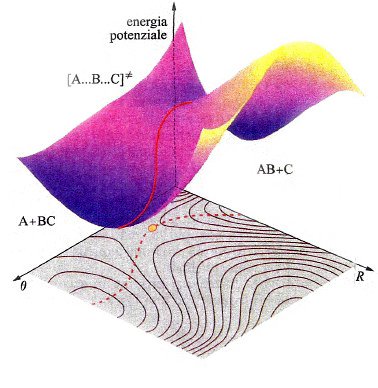
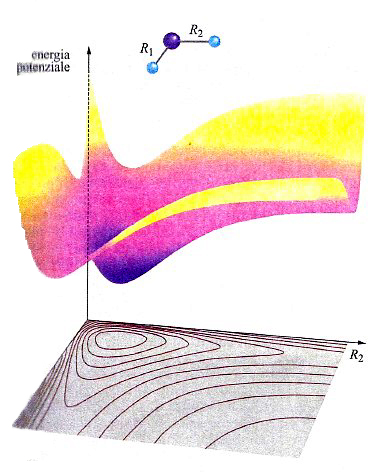
In una molecola triatomica, quale l'acqua, la descrizione dell'andamento dell'energia potenziale richiede l'impiego di un diagramma tridimensionale come quello illustrato nella fig. 14, nel quale i valori dell'energia sono descritti da una superficie il cui andamento dipende dalle distanze tra i due atomi di idrogeno e quello di ossigeno. La superficie così ottenuta viene indicata mediante l'acronimo PES (Potential Energy Surface). In realtà, tale descrizione non è completa, poiché assume implicitamente che l'angolo fra i legami O−H sia mantenuto costante. Questo fatto mette in evidenza la difficoltà di descrivere graficamente le PES, poiché per una molecola non lineare costituita da n atomi sarebbe richiesto uno spazio di 3n-5 dimensioni. Malgrado questa limitazione, le PES si rivelano molto utili per lo studio del meccanismo delle reazioni chimiche. Consideriamo ad esempio una reazione di sostituzione del tipo:
A + BC →AB + C. (35)
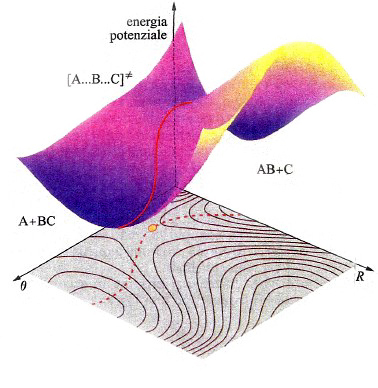
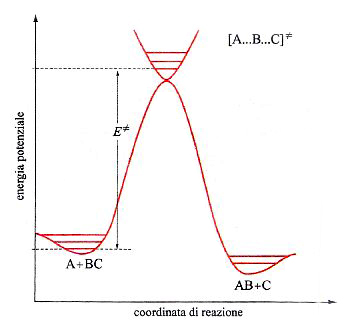
In questo caso la PES che descrive il passaggio dai prodotti ai reagenti con la rottura e la formazione dei corrispondenti legami ha il tipico andamento descritto nella fig. 15. La linea rossa individua un particolare percorso caratterizzato dal fatto che il valore locale dell'energia in ogni punto del cammino è minimo rispetto a spostamenti a esso perpendicolari. Se si riporta l'energia lungo tale coordinata di reazione, si ottiene la curva illustrata in fig. 16, nella quale viene evidenziato che il passaggio dai reagenti ai prodotti è condizionato dal superamento di una barriera di energia potenziale. La differenza E≠ fra le energie di punto zero del massimo e dei reagenti si identifica con l'energia di attivazione della reazione. Poiché la conoscenza delle PES è indispensabile per poter calcolare le velocità delle reazioni chimiche, ne consegue che le difficoltà incontrate per una loro accurata determinazione costituiscono la maggiore strozzatura incontrata per raggiungere tale obiettivo. Fortunatamente i recenti sviluppi della chimica computazionale offrono la possibilità di perseguire lo scopo anche per reazioni relativamente complesse, aprendo così ampie prospettive nel panorama della cinetica chimica.
La dinamica di una collisione può essere studiata descrivendo il moto del punto che rappresenta il sistema reagente sulla PES mediante la meccanica classica (v. reazioni chimiche, dinamica delle, vol. XI). Integrando numericamente le equazioni del moto si simulano le traiettorie descritte dal punto rappresentativo, compatibilmente con diverse condizioni iniziali che caratterizzano lo stato delle molecole reagenti, in particolare la loro posizione relativa e la loro energia. Le traiettorie che superano la barriera di energia potenziale corrispondono a collisioni reattive, per cui attraverso l'esame di un numero ragionevolmente elevato di tali collisioni, campionate a caso per quanto concerne l'energia e l'orientazione relativa delle molecole, si valuta la probabilità che abbia luogo la reazione. In realtà i calcoli per ottenere informazioni dettagliate sugli eventi microscopici in gioco sono molto onerosi, per cui la loro applicazione rimane ancora limitata a sistemi molecolari semplici. La maggiore difficoltà risiede nel fatto che a ogni passo di integrazione delle equazioni del moto è necessario valutare le funzioni d'onda e l'energia dell'intero sistema. Un metodo efficace per ovviare a questo inconveniente è quello proposto da Roberto Car e Michele Parrinello (v., 1985): dopo aver valutato con il metodo DFT gli orbitali ϕkℓ(r) del punto di inizio, essi vengono sviluppati in onde piane. Questa scelta è inconsueta nella chimica quantistica, mentre è comune nella fisica della materia condensata e offre alcuni vantaggi fra i quali la facilità dei calcoli numerici. I coefficienti dello sviluppo crk vengono trattati come una serie di variabili dinamiche che si evolvono in modo simultaneo alla variazione delle posizioni nucleari. Lo scopo viene conseguito attribuendogli una massa fittizia μ opportunamente scelta, ad esempio facendo in modo che la distribuzione degli elettroni sia prossima a quella della configurazione di Born-Oppenheimer.
Dal punto di vista formale si procede in accordo alla meccanica classica introducendo una lagrangiana espressa come segue:
formula (36)
dove E[ϕk, S] è l'energia del sistema riferita a una particolare configurazione nucleare indicata collettivamente con S e calcolata mediante il metodo DFT, mentre i punti indicano le derivate rispetto al tempo. Per semplicità è stata inoltre adottata la notazione di Dirac ∫ ϕk*ϕℓdr = 〈 ϕk|ϕℓ 〉, mentre l'ultimo termine al secondo membro viene introdotto per imporre che gli orbitali soddisfino le condizioni di ortonormalità indicate nella (1). Λkℓ sono i corrispondenti parametri di Lagrange.
In questa impostazione i gradi di libertà del sistema sono le coordinate nucleari Rα e i coefficienti crk degli orbitali. Lo studio del comportamento dinamico consegue dall'applicazione alla (36) delle equazioni di Eulero-Lagrange, da cui si ottiene:
formula (37)
formula (38)
L'integrazione delle equazioni precedenti, a partire da una configurazione iniziale, permette di ricavare la dipendenza delle crk e delle Rα dal tempo e quindi di descrivere la dinamica di sistemi molecolari attraverso l'evoluzione della loro configurazione geometrica e della densità elettronica verso una situazione di equilibrio caratterizzata da un valore minimo dell'energia. Il metodo è particolarmente adeguato per piccoli aggregati atomici e per studiare la struttura delle superfici. Più recentemente è stato applicato anche alla descrizione del comportamento dinamico di sistemi molecolari di rilevanza biologica (v. Carloni e altri, 2002).
Di fatto, se si escludono reazioni molto veloci è ragionevole assumere che esista una distribuzione di equilibrio fra i diversi moti molecolari interni, eccetto ovviamente quello lungo la coordinata di reazione. Se si assume che alla sommità della barriera di energia esista una regione della PES che porta alla reazione, il calcolo della probabilità che essa venga raggiunta si può effettuare con i metodi della termodinamica statistica. La velocità di reazione R viene allora valutata come flusso medio dei reagenti che attraversa tale regione ed espressa dalla relazione seguente:
formula (39)
essendo CA e CBC le concentrazioni dei reagenti e kB la costante di Boltzmann. ΔG≠ è la variazione di energia libera, detta 'di attivazione', associata al passaggio dai reagenti allo stato di transizione, ovvero a quel complesso molecolare instabile ('complesso attivato') che si trova alla sommità della barriera di energia potenziale, in corrispondenza della configurazione [A...B...C]≠ nella quale il legame A−B non è ancora del tutto formato e quello B−C non è completamente rotto. Malgrado la sua esistenza effimera (10-12 ÷ 10-11 s), le caratteristiche geometriche e le frequenze di vibrazione atomiche del complesso [A...B...C]≠ possono essere calcolate dall'andamento della PES nell'intorno della zona della sua esistenza. Utilizzando queste informazioni si può facilmente risalire alla ΔG≠ e quindi, mediante la (39), alla costante di velocità della reazione.
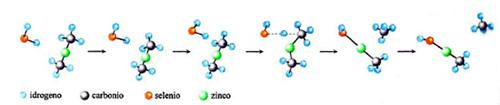
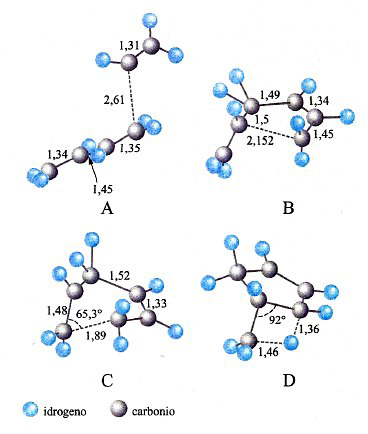
Nella letteratura recente si trovano diversi esempi in cui le PES vengono applicate sia nella delucidazione del meccanismo di particolari reazioni, sia nella valutazione della loro velocità. A scopo illustrativo verranno qui presentati alcuni di questi esempi. Il primo è riportato nella fig. 17, dove viene illustrata l'evoluzione di una delle reazioni coinvolte nel processo di sintesi di un materiale di interesse nell'optoelettronica, il seleniuro di zinco, ZnSe. Il cammino della reazione fra seleniuro di idrogeno e zinco dimetile è stato simulato valutando l'energia delle due molecole che entrano in collisione per diverse posizioni relative, incluse quelle corrispondenti allo stato di transizione. Il prodotto ottenuto (CH3ZnSeH) interagisce successivamente con la superficie del solido depositando ZnSe. Un altro esempio si riferisce all'esame dell'influenza dei processi di combustione sulla composizione dell'ambiente atmosferico. Come menzionato, la combustione degli idrocarburi procede attraverso un numero molto elevato di reazioni elementari che coinvolgono composti instabili di natura radicalica, contenenti, cioè, un elettrone spaiato. Essi si formano per dissociazione delle molecole degli idrocarburi in conseguenza delle elevate temperature che vengono raggiunte. In virtù della loro reattività, tali specie intervengono in diverse reazioni che possono portare alla formazione di inquinanti, quali ad esempio gli ossidi di azoto e piccole particelle di carbonio che si presentano sotto forma di una polvere sottile, nociva per gli organismi. Pertanto, per gestire i processi di combustione in modo da limitare la formazione di tali inquinanti è necessario individuare opportune condizioni operative. Questo obiettivo può essere perseguito attraverso la delucidazione dei meccanismi delle reazioni coinvolte nel processo e quindi mediante la valutazione delle loro velocità. Tutto ciò esplorando con la simulazione numerica diversi possibili cammini di reazione per evidenziare quelli che, essendo più veloci, condizionano in modo prevalente la natura dei prodotti formati. In questo quadro, può essere interessante approfondire il meccanismo di formazione del benzene e dei suoi derivati, i quali per ulteriore condensazione danno origine alle particelle carboniose solide. Mediante la teoria dello stato di transizione è stato possibile dimostrare che i precursori sono idrocarburi ciclici alifatici non solo a 6, ma anche a 5 atomi di carbonio. In quest'ultimo caso, ad esempio, sono coinvolte le reazioni riportate in fig. 18, la cui velocità è stata calcolata sulla base delle caratteristiche dei complessi attivati illustrati nella figura stessa.
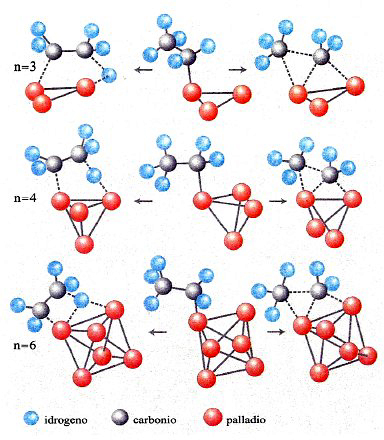
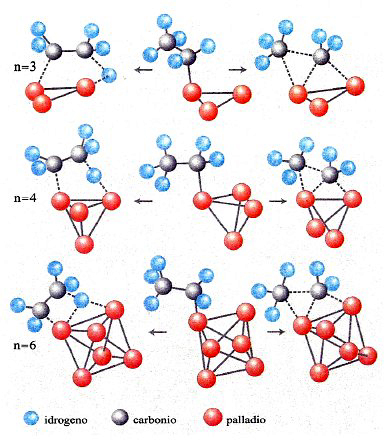
Un ulteriore esempio riguarda la catalisi eterogenea e si riferisce specificamente alle trasformazioni, di interesse nei settori energetico e petrolchimico, che subiscono gli idrocarburi alifatici in presenza di metalli di transizione quali il nichel, il platino e il palladio. In particolare, possono avere luogo sia reazioni di deidrogenazione, con eliminazione di una molecola di idrogeno e formazione di un idrocarburo insaturo, sia di idrogenolisi, con la scissione in due nuove molecole di idrocarburi alifatici in seguito all'interazione con una molecola di idrogeno. Anche in questo caso intervengono diversi stadi che coinvolgono l'adsorbimento dei reagenti sugli atomi del catalizzatore e le successive trasformazioni da essi subite. In tale quadro risulta ragionevole assumere che entrambe le reazioni menzionate procedano attraverso un intermedio comune costituito da un radicale alchilico legato a un atomo del catalizzatore. La sua successiva evoluzione avviene attraverso due cammini paralleli che coinvolgono complessi attivati aventi le strutture illustrate in fig. 19, dove si fa riferimento al palladio quale catalizzatore (v. Bertani e altri, 2000 e 2001). Per approfondire l'analisi sono stati considerati centri attivi che coinvolgono diversi atomi di palladio, valutando per ciascuno di essi i corrispondenti parametri cinetici, dal cui esame è possibile evidenziare il peso relativo delle due reazioni e la loro maggiore o minore dipendenza dalla struttura del catalizzatore.
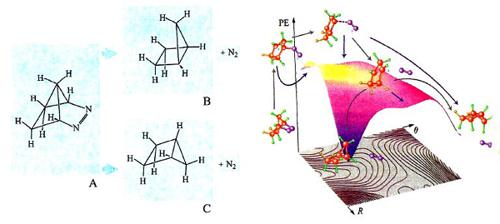
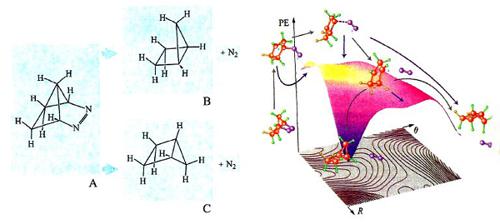
L'impiego delle PES è spesso illuminante nell'esame dei dettagli del meccanismo di reazioni che possono portare a prodotti diversi. A titolo di esempio, consideriamo la reazione riportata nella fig. 20 (a sinistra), nella quale l'azocomposto A per eliminazione di una molecola di azoto si converte in un idrocarburo biciclico che può esistere nelle due configurazioni steriche B e C. L'osservazione sperimentale mostra che il principale prodotto di reazione è l'isomero C. La PES della reazione è illustrata nella parte destra della figura, nella quale vengono riportati anche i cammini delle possibili reazioni che includono la partecipazione di intermedi biradicalici, ovvero con due elettroni spaiati. Il loro studio dinamico ha permesso di determinare in che modo la distribuzione dell'energia di vibrazione nei diversi intermedi condizioni la loro stabilità relativa, giustificando la formazione privilegiata di un particolare isomero.
Una prospettiva di frontiera che sta acquistando sempre maggiore rilevanza è la simulazione dei processi chimici che avvengono nei sistemi biologici; in particolare, risulta di interesse determinare la velocità delle reazioni catalizzate da enzimi. In linea di principio l'approccio che viene seguito non differisce da quello precedentemente descritto, se si escludono le maggiori difficoltà dovute alla complessità dei sistemi esaminati. Inoltre, poiché molte di tali reazioni coinvolgono il moto di protoni, è necessario includere l'effetto tunnel, un fenomeno di natura quantistica in virtù del quale i protoni hanno una probabilità non trascurabile di attraversare le barriere di energia potenziale. Infine, è necessario tenere adeguato conto degli effetti quantistici valutando con accuratezza l'energia di punto zero. La complessità delle strutture molecolari che intervengono nelle reazioni biologiche ha suggerito di adottare un approccio gerarchico introdotto originariamente per studiare la cinetica di reazioni che avvengono in soluzione (v. Gao, 1996). Si localizza la zona chimicamente attiva della molecola, isolandola da tutto il resto, e si tratta la dinamica dei processi che hanno luogo in tale zona mediante la meccanica quantistica e la teoria dello stato di transizione. Viceversa, i movimenti molecolari che si verificano nella parte esterna vengono descritti mediante la meccanica classica, assimilando gli atomi a sfere di van der Waals e utilizzando potenziali empirici di agevole impiego. Questo approccio, indicato con l'acronimo QM/MM (Quantum Mechanics/Molecular Mechanics), è basato quindi sull'impiego di una hamiltoniana mista del tipo:
Ĥ = ĤQM + ĤMM +ĤQM −MM (40)
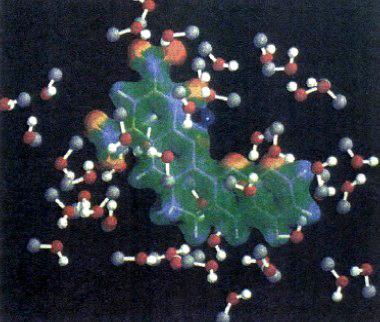
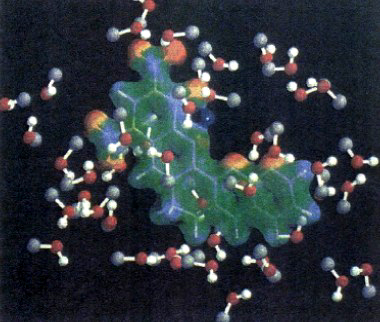
dove ĤQM è l'hamiltoniana quantistica, ĤMM quella classica e infine ĤQM-MM è il termine di interazione che riflette le condizioni relative al contorno fra le due zone. Un esempio di come possa essere effettuata tale ripartizione è illustrato nella fig. 21, che si riferisce alla creatinina sciolta nel metanolo. La creatinina viene rappresentata mediante il campo elettrostatico che circoscrive la sua densità elettronica, mentre le molecole del solvente (il metanolo) sono rappresentate come sfere di van der Waals.
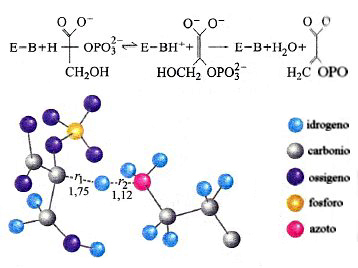
Infine, a titolo di esempio nella fig. 22 viene illustrata la struttura dello stato di transizione relativo al processo di trasferimento protonico di una tipica reazione enzimatica. Si tratta della disidratazione del 2-fosfo-D-glicerato (2-PGA) a fosfoenolpiruvato (PEP) per azione di un enzima basico E-B, che procede attraverso due stadi. Il primo di essi, che coinvolge il trasferimento di un protone fra la PEP e l'E-B, passa attraverso uno stato di transizione le cui caratteristiche, per quanto concerne il sottosistema descritto mediante la meccanica quantistica, sono quelle illustrate nella figura.
10. Conclusioni
Lo sviluppo dei metodi di calcolo della struttura elettronica delle molecole con procedimenti ab initio sta offrendo ai chimici raffinati strumenti di calcolo sino a qualche anno fa considerati prerogativa di ricercatori specializzati. Risulta infatti possibile valutare con notevole accuratezza proprietà molecolari quali la geometria, le frequenze di vibrazione, la distribuzione delle cariche, le interazioni fra diverse molecole e la velocità delle reazioni che traggono origine dalle loro collisioni. Nella trattazione sviluppata in questo articolo sono state illustrate diverse metodologie che possono essere opportunamente scelte in relazione al problema specifico da affrontare e al grado di accuratezza che si vuole ottenere. Tuttavia, si deve anche osservare che la chimica computazionale è ancora una disciplina in fase di sviluppo e non ha raggiunto una piena maturità. I problemi aperti riguardano settori molto diversificati quali lo studio delle molecole di grandi dimensioni, delle interazioni fra molecole e superfici, e dei sistemi molecolari bio-organici. Inoltre, i maggiori successi sino a ora conseguiti riguardano molecole isolate o presenti in fase gassosa, mentre molto resta ancora da fare per sistemi in fase condensata. Sotto questo aspetto i metodi di calcolo delle strutture elettroniche devono opportunamente integrarsi con la termodinamica statistica.
Si deve comunque riconoscere che i progressi realizzati in questi ultimi anni hanno contribuito a emancipare la chimica teorica computazionale da un ambito strettamente concettuale, rendendola uno strumento di più largo impiego.
bibliografia
Aihara, J., Why aromatic compounds are stable, in "Scientific American", 1992, CCLXVI, 3, pp. 44-51 (tr. it.: La stabilità dei composti aromatici, in "Le scienze", 1992, CCLXXXV, pp. 66-74).
Alhambra, C. e altri, Quantum mechanical dynamical effects in an enzyme-catalyzed proton-transfer reaction, in "Journal of the American Chemical Society", 1999, CXXI, pp. 2253-2258.
Atkins, P. W., Friedman, R. S., Molecular quantum mechanics, Oxford: Oxford University Press, 19973 (tr. it.: Meccanica quantistica molecolare, Bologna: Zanichelli, 2000).
Bertani, V., Cavallotti, C., Masi, M., Carrà, S., Density functional study of the interaction of palladium clusters with hydrogen and CHx species, in "The journal of physical chemistry A", 2000, CIV, pp. 11390-11397.
Bertani, V., Cavallotti, C., Masi, M., Carrà, S., Kinetic study of hydrocarbons reactivity on palladium catalysts through a DFT approach, in Spring meeting proceedings of the general symposium AA "Advances in materials theory and modeling-bridging over multiple-length and time scales" (a cura di V. Bulatov e altri), Warrendale, Pa.: Materials Research Society, 2001, p. AA8.6.
Car, R., Parrinello, M., Unified approach for density functional theory and molecular dynamics, in "Physical review letters", 1985, LV, pp. 2471-2474.
Carloni, P., Rothlisberger, U., Parrinello, M., The role and perspective of ab initio molecular dynamics in the study of biological systems, in "Accounts of chemical research", 2002, XXXV, pp. 455-464.
Carpenter, B. K., Reaction dynamics in organic chemistry, in "American scientist", 1997, LXXXV, pp. 138-149.
Carrà, S., Elettroni, atomi e trasformazioni: la chimica cento anni dopo la scoperta di J. J. Thomson, in Centenario della scoperta dell'elettrone. Atti del simposio, Roma, 13 novembre 1997, Roma: Accademia Nazionale dei Lincei, 1998, pp. 49-72.
Cavallotti, C., Rota, R., Carrà, S., Quantum chemistry computation of rate constants for reactions involved in the first aromatic ring formation, in "The journal of physical chemistry A", 2002, CVI, pp. 7769-7778.
Gao, J., Hybrid quantum and molecular mechanical simulations: an alternative avenue to solvent effects in organic chemistry, in "Accounts of chemical research", 1996, XXIX, pp. 298-305.
Head-Gordon, M., Quantum chemistry and molecular processes, in "The journal of physical chemistry", 1996, C, pp. 13213-13225.
Hehre, W. J. e altri, Ab initio molecular orbital theory, New York: Wiley, 1986.
Jensen, F., Introduction to computational chemistry, New York: Wiley, 1999.
Kohn, W., Becke, A. D., Parr, R. G., Density functional theory of electronic structure, in "The journal of physical chemistry", 1996, C, pp. 12974-12980.
Levine, N., Quantum chemistry, Englewood Cliffs, N. J.: Prentice Hall, 19914.
Linnett, J. W., Wave mechanics and valency, London: Methuen, 1960.
Parr, R. G., Yang, W., Density-functional theory of atoms and molecules, Oxford: Oxford University Press, 1989.
Pople, J. A., Quantum chemical models (Nobel lecture), in "Angewandte Chemie. International edition", 1999, XXXVIII, pp. 1895-1902.
Raghavachari, K., Anderson, J. B., Electron correlation effects in molecules, in "The journal of physical chemistry", 1996, C, pp. 12960-12973.
Truhlar, D. G., Garrett, B. C., Klippenstein, S. J., Current status of transition-state theory, in "The journal of physical chemistry", 1996, C, pp. 12771-12800.
Wigner, E. P., The unreasonable effectiveness of mathematics in the natural sciences, in "Communications in pure and applied mathematics", 1960, XIII, pp. 1-14.
Zewail, A. H., Femtochemistry: recent progress in studies of dynamics and control of reactions and their transition states, in "The journal of physical chemistry", 1996, C, pp. 12701-12724.