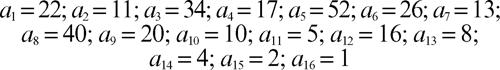Ulam, congettura di

Ulam, congettura di

Ulam, congettura di o congettura di Collatz, congettura enunciata per la prima volta nel 1937 dal matematico tedesco L. Collatz, da cui il nome con cui è anche nota. È pure conosciuta come congettura 3n + 1, per il suo contenuto. Essa riguarda la sequenza numerica così definita ricorsivamente: si assegna come valore iniziale a₀ un intero positivo n qualunque; ogni termine a_n è la metà del precedente se tale precedente è pari; se invece il precedente è dispari, allora a_n è uguale al precedente moltiplicato per 3 e addizionato a 1. La sequenza si ferma se a_n = 1. Formalmente, la regola che genera la sequenza è la seguente:

La congettura, che porta tale nome perché fu avvalorata anche dal fisico e matematico statunitense S.M. Ulam, afferma che qualunque sia il numero naturale iniziale a₀ non nullo, dopo un certo numero di applicazioni della regola (numero che dipende da a₀), si ottiene 1 e quindi la sequenza ha un termine. Formalmente: ∀a₀ ∈ N₀, ∃k(a₀) ∈ N : a_k = 1. Per esempio, se si sceglie a₀ = 42, si ottiene 1 all’ottava applicazione della regola:

Se invece si sceglie a₀ = 7, si ottiene 1 al sedicesimo passaggio:

Si noti che se, pervenuti a 1, si ripetesse la regola, si otterrebbe una sequenza di valori (4, 2, 1) che si ripeterebbe all’infinito. Infatti, se per qualche k si ottiene a_k = 1 e si volesse proseguire con la medesima regola ricorsiva, si otterrebbe:

e così via. Pur essendo stata verificata fino a numeri naturali iniziali con un ordine di grandezza pari a 10¹⁸, a tutt’oggi (2013), la congettura non è stata dimostrata. La successione che si ottiene è anche detta sequenza di Hailstone (sequenza del chicco di grandine), perché, come i chicchi di grandine che in una nuvola salgono e scendono turbinosamente, così i valori di tale sequenza, prima di arrivare al valore 1, aumentano e diminuiscono in modo apparentemente imprevedibile.