convessita

convessita

convessità proprietà di una figura, di un insieme, di una funzione.

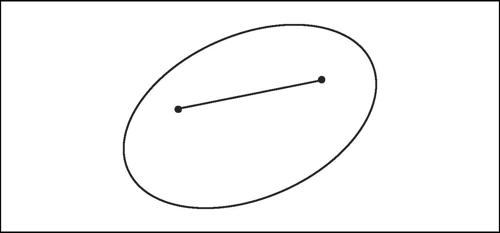
☐ In geometria, proprietà di una figura piana o solida consistente nel fatto che qualunque segmento avente per estremi due punti della figura giace interamente in essa. Una figura con tale proprietà è detta figura convessa o insieme convesso. Un angolo è convesso quando è piatto o non contiene i prolungamenti dei lati; è, quindi, minore o uguale a un angolo piatto. Un poligono è convesso se tutti i suoi angoli sono convessi e, quindi, giace tutto da una stessa parte rispetto alla retta di ciascun lato. Ne consegue che tutti i triangoli sono convessi. L’intersezione di due insiemi convessi è un insieme convesso; l’unione di due insiemi convessi in genere non è un insieme convesso. Nello spazio euclideo tridimensionale sono esempi di insiemi convessi il cubo, la sfera, un semispazio.

☐ Più in generale, un sottoinsieme A di uno spazio vettoriale reale è convesso nel caso in cui se a e b sono due punti qualsiasi di A, allora è contenuto in A anche l’insieme di tutti i punti dello spazio del tipo ta + (1 − t)b, con 0 ≤ t ≤ 1 (detta appunto combinazione convessa di a e b). Uno spazio vettoriale topologico si dice localmente convesso se ogni aperto contiene un sottoinsieme aperto convesso. Ogni spazio normato è localmente convesso. Sussistono teoremi di separazione fra insiemi convessi. Se A è aperto e convesso e B è convesso e disgiunto da A, allora A e B sono separati da un iperpiano, ossia esistono un funzionale lineare ƒ e un numero reale c tali che ƒ(a) ≤ c ≤ ƒ(b) per tutti gli a di A e b di B. Se A è convesso, un punto a di A si dice estremo se esso non fa parte di nessun segmento con estremi appartenenti ad A e distinti da a; un punto a si dice esposto se esiste un iperpiano chiuso di supporto ad A in a che intersechi A soltanto in a; ogni punto esposto è anche estremo. L’insieme A si dice strettamente convesso se tutti i suoi punti di frontiera sono esposti.

☐ In analisi, il termine convessità è utilizzato per indicare la caratteristica di una funzione continua ƒ(x), di una variabile reale, il cui grafico giace al di sopra della retta tangente in quel punto, ammesso che esista (→ funzione convessa). Condizione sufficiente affinché in un intervallo la funzione ƒ(x) sia convessa è che per ogni x interno all’intervallo ƒ″(x) > 0.