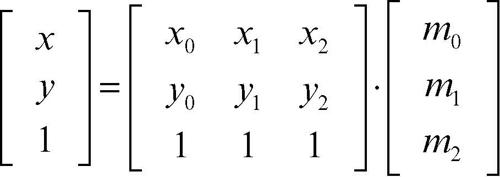coordinate baricentriche

coordinate baricentriche

coordinate baricentriche particolare tipo di coordinate omogenee definite a partire da un simplesso; possono essere definite per un punto di uno spazio euclideo, o più in generale di uno spazio vettoriale o affine di dimensione n (in quest’ultimo caso sono dette coordinate affini). Le coordinate baricentriche sono note anche come coordinate di Möbius, dal nome del matematico tedesco A.F. Möbius, che le introdusse per primo nel 1827. Nel caso bidimensionale, per esempio il piano R², un simplesso è costituito da un triangolo. Fissati pertanto in R² tre punti non allineati V₀, V₁, V₂ (vertici del triangolo), la terna ordinata di numeri (m₀, m₁, m₂) costituisce le coordinate baricentriche di un punto P del piano se sono verificate le seguenti condizioni:

• P = m₀V₀ + m₁V₁ + m₂V₂

• m₀ + m₁ + m₂ = 1

(condizione di normalizzazione)

La condizione di normalizzazione rende univoche le coordinate baricentriche. Un punto è interno al triangolo se e solo se ha coordinate baricentriche positive. Per i punti non esterni al triangolo le coordinate baricentriche hanno un significato fisico che è all’origine della loro denominazione: (m₀, m₁, m₂) rappresentano i rapporti tra le masse che, poste rispettivamente nei vertici V₀, V₁, V₂, hanno come centro di massa il punto P. In particolare, considerando i punti V₀(1, 0, 0), V₁(0, 1, 0), V₂(0, 0, 1), le equazioni m₀ = 0, m₁ = 0, m₂ = 0 rappresentano, rispettivamente, le rette V₁ V₂, V₀ V₂, V₀ V₁.

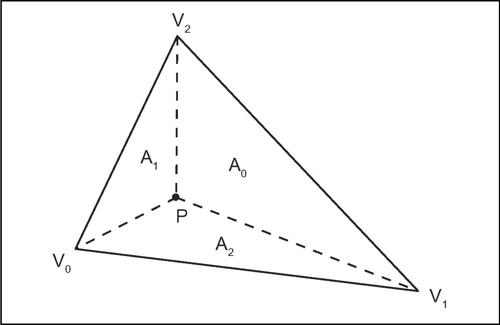
Le coordinate baricentriche sono anche interpretabili in termini geometrici. Con riferimento alla figura, si ha che le coordinate di P sono

avendo indicato con A l’area del triangolo di riferimento. Il passaggio dalle coordinate baricentriche alle coordinate cartesiane, indicate con (x_i, y_i) le coordinate cartesiane dei tre vertici V_i del triangolo, avviene risolvendo il sistema lineare

Tale sistema ha soluzione se e solo se la matrice 3 × 3 a secondo membro è non singolare, cioè se e solo se il triangolo non è degenere. La definizione data si estende dal piano a uno spazio di dimensione n. Assegnato per esempio in Rⁿ un simplesso di vertici V₀, V₁, …,V_n, gli n + 1 numeri reali (m₀, m₁, …, m_n) sono le coordinate baricentriche di un punto P ∈ Rⁿ se verificano le seguenti condizioni:

• P = m₀V₀ + m₁V₁ + ... + m_nV_n

• m₀ + m₁ + … + m_n = 1

(condizione di normalizzazione)

La condizione di normalizzazione rende univoche le coordinate baricentriche. Le coordinate baricentriche di un punto sono invarianti per trasformazioni affini. Al pari delle coordinate proiettive omogenee, con le quali sostanzialmente coincidono, le coordinate baricentriche permettono di trattare analiticamente allo stesso modo elementi propri (al finito) ed elementi impropri (all’infinito). Si veda anche → rapporto semplice di tre punti allineati.