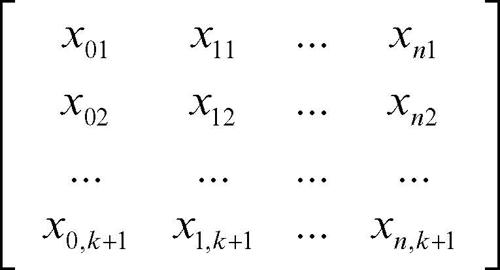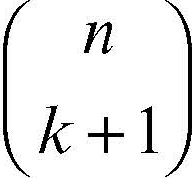coordinate pluckeriane
coordinate pluckeriane
coordinate plückeriane in geometria analitica, sistema di coordinate nel piano proiettivo atto a individuare sottoinsiemi dello spazio di riferimento. Prende il nome dal matematico tedesco J. Plücker che lo introdusse negli anni 1828-35 nelle opere in cui espone il nuovo sistema della geometria analitica in relazione alla geometria proiettiva. Per esempio, data l’equazione di una retta del piano in coordinate omogenee a0x0 + a1x1 + a2x2 = 0 con a0, a1, a2 ∈ R, le sue coordinate plückeriane, definite a meno di un fattore di proporzionalità non nullo, sono la terna ordinata (a0, a1, a2). In generale, in uno spazio proiettivo Sn di dimensione n, se Sk è un sottospazio di dimensione k < n e P1, P2, …, Pk+1 sono k + 1 punti che lo generano, si considera la matrice avente per righe le coordinate omogenee dei k + 1 punti P1, P2, …, Pk+1
i minori di ordine k + 1 estratti dalla matrice, che sono in numero di
dove il simbolo indica il coefficiente binomiale, sono detti coordinate grassmanniane del sottospazio Sk se k > 1; se invece k = 1 sono detti coordinate plückeriane.