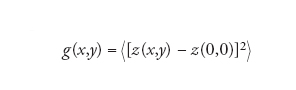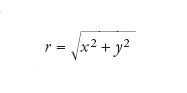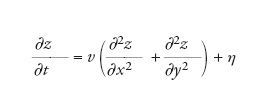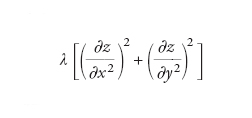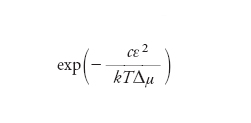Crescita di superfici

Crescita di superfici

In generale, le scienze tendono a spostare i loro interessi sempre più verso i fenomeni evolutivi. Probabilmente la maggior parte di esse studia dapprima i fenomeni stazionari o di equilibrio (i due termini non sono sinonimi) non perché siano più interessanti, ma perché sono più semplici e soprattutto definiti più univocamente. L'evoluzione dipende dalle condizioni iniziali ma spesso conduce a qualche stato di equilibrio, o almeno a qualche stato stazionario, indipendente da tali condizioni. Non sorprende quindi che gli scienziati siano stati tentati di focalizzare la loro attenzione su questo stato finale anziché sulla moltitudine di processi evolutivi che conducono a esso. Nonostante ciò, negli ultimi anni i processi evolutivi sono diventati l'oggetto centrale della ricerca in molti campi. La crescita dei cristalli è un caso storicamente un po' speciale perché, a motivo della sua importanza pratica, fu studiato in dettaglio già molto tempo prima che una parte rilevante della comunità scientifica focalizzasse la propria attenzione verso i fenomeni evolutivi. Recentemente, però, è diventato sempre più chiaro che essa è parte di un insieme di fenomeni molto più vasto, che costituisce l'oggetto di una scienza della crescita alla quale sono stati dedicati diversi libri e lavori di rassegna. La stessa crescita dei cristalli (che avviene per sua natura spostando a favore del cristallo la superficie di separazione fra il cristallo stesso e il fluido con cui è in contatto) dev'essere ormai vista, soprattutto sul piano microscopico, come una crescita di superficie.

La scienza della crescita si occupa dei fenomeni più diversi, dalla crescita di un tumore maligno a quella delle corna di un cervo, dal diffondersi di una religione a quello di un incendio boschivo. Tutti questi fenomeni hanno qualcosa in comune. Molto spesso si hanno due punti di vista possibili, locale e globale, non indipendenti, ma tra loro piuttosto diversi. In ogni caso, il problema della crescita sarà ben impostato se lo si potrà esprimere per mezzo di equazioni differenziali che abbiano fra le incognite i parametri che la definiscono. Nel caso della crescita di superficie si potrebbe avere, come parametro locale, il suo livello z=ζ(x,y,t). Da un punto di vista globale, invece, il solido può essere per esempio definito come un dominio tridimensionale dotato di una frontiera, in certi casi multiplamente connessa: il livello della superficie ne sarà l'immagine locale vista perpendicolarmente a un asse locale di crescita scelto come asse z. Alla crescita di superficie possono essere associate equazioni come quelle di Samuel F. Edwards e David R. Wilkinson, di Mehran Kardar, Giorgio Parisi e Yi-Cheng Zhang, di Siu-Tat Chui e John D. Weeks, mentre l'approccio globale è stato seguito e trattato dal punto di vista teorico da Robert F. Sekerka, da James S. Langer e dai loro collaboratori. I due punti di vista sono, apparentemente, totalmente diversi, tuttavia è importante sottolineare in che senso sono in rapporto tra loro.

È interessante considerare la crescita di superfici come problema matematico. I modelli matematici, pur trascurando molte complicazioni accidentali, possono dar luogo a problemi di grande complessità. L'evoluzione temporale ha caratteristiche non banali e possono anche nascere strutture spaziali complesse, legate all'instabilità intrinseca dei fenomeni. Può essere opportuna una trattazione che proceda dal semplice al complicato e, certamente, dal locale al globale. I modelli matematici, tipicamente, non tengono conto della struttura atomica e, dal punto di vista fisico, si riferiscono a scale spaziali grandi rispetto a quella degli atomi e a scale temporali molto più lunghe della durata caratteristica di un singolo evento atomico; possono quindi basarsi su una descrizione continua e su equazioni differenziali. È necessario, tuttavia, distinguere due trattazioni diverse: l'una, più microscopica, fa riferimento a equazioni differenziali stocastiche; l'altra focalizza l'attenzione sulle instabilità e sulla generazione di strutture spaziali complesse, e in particolare sulla crescita dendritica.

Il liscio e il ruvido

Una caratteristica importante di una superficie è la ruvidità, definita come segue. Si consideri la differenza quadratica media tra una posizione (x,y) e un'altra (0,0) scelta come origine:

[1] formula

ovviamente g(0,0) è nulla, mentre g cresce al crescere di

[2] formula.

Se g rimane finita, la superficie è liscia; se diverge all'infinito, la superficie è ruvida e la legge con cui g diverge definisce il carattere della ruvidità. La superficie di un solido in equilibrio può essere liscia o ruvida, ma si può dimostrare che esiste una temperatura d'irruvidimento T_R al di sotto della quale la superficie è certamente liscia. Sopra T_R, invece, se il solido non fonde prima, la superficie diventa ruvida. Si ha dunque una transizione liscio-ruvido (roughening transition), rivelatasi di fondamentale importanza nella meccanica statistica delle superfici. La stessa cosa può avvenire per la superficie di un solido in crescita, presumibilmente con una temperatura d'irruvidimento più bassa. I modelli matematicamente più semplici descrivono una superficie in crescita come ruvida, ma complicandoli un poco si può ottenere, almeno in prima approssimazione, una superficie liscia.

Equazioni differenziali stocastiche

In un problema di crescita, almeno nei casi più semplici, si può rappresentare l'altezza della superficie (che cresce nella direzione z) per mezzo di una funzione z(x,y,t) che cresce con il tempo t. Questa funzione z corrisponde a una velocità verticale v=∂z/∂t che dipende dalla forma della superficie a un certo istante e quindi dalle derivate ∂z/∂x e ∂z/∂y. In generale v dipenderà anche da fattori casuali, con ogni sorta di fluttuazione, per esempio, in un problema di crescita cristallina l'arrivo disordinato degli atomi sul cristallo. Il contributo casuale a v è solitamente chiamato 'rumore', per analogia con l'acustica e con l'elettronica circuitale. Le equazioni che così si ottengono sono dette 'equazioni differenziali stocastiche' e hanno proprietà ben diverse dalle equazioni differenziali ordinarie.

La più semplice di tali equazioni differenziali stocastiche per la crescita fu introdotta da Sam F. Edwards e David R. Wilkinson nel 1982, nel contesto della crescita di un aggregato granulare, e ha la forma esplicita

[3] formula

dove η è il rumore, ossia un contributo aleatorio. L'equazione di Edwards-Wilkinson (EW) è lineare, può essere risolta esattamente e ha proprietà interessanti, ma presto si è capito che non può descrivere tutti i casi fisicamente importanti. La soluzione dà luogo a una variazione quadrata media dell'altezza g(x,y) che si comporta (per grandi distanze r) come il logaritmo di r, cioè dà luogo a una ruvidità logaritmica. Aggiungendo al secondo membro termini quadratici del tipo

[4] formula

si ottiene l'equazione di Kardar, Parisi e Zhang (KPZ), di non facile soluzione ma molto studiata perché è la più semplice modifica non lineare dell'equazione di EW. L'equazione di KPZ genera superfici la cui ruvidità può seguire una legge di potenza, più forte che non logaritmica.

Accade il contrario se all'equazione di EW si aggiunge, invece, un termine sinusoidale del tipo Y sen(2πz/a), che favorisce i livelli z=na e, dunque, una struttura cristallina di passo a. Si ottiene così l'equazione di Chui e Weeks (CW) ‒ scritta già nel 1978, prima che Edwards e Wilkinson ricavassero la loro. Le superfici generate dall'equazione di CW sono meno ruvide di quelle di EW e possono essere addirittura lisce. Nel 1984 Philippe Nozières e François Gallet mostrarono che, in condizioni di crescita, la transizione liscio-ruvido avviene a temperature un po' inferiori alla temperatura di transizione T_R e tanto più basse quanto più è veloce la crescita. Questa proprietà fu dimostrata sperimentalmente nel caso della crescita dell'elio solido dal superfluido e successivamente chiarita da vari punti di vista (nucleazione di isole, simulazioni di crescita). Una delle trattazioni più complete è stata presentata nel 1991 da Terry Hwa, Mehran Kardar e Maya Paczuski, che includono tutte e due le perturbazioni sopraindicate e ottengono un'interessante descrizione della transizione liscio-ruvido per una superficie in crescita.

Modi di crescita

Da molto tempo si classifica la crescita dei cristalli a seconda del cosiddetto modo di crescita. Si riconoscono almeno quattro modi di crescita diversi: la crescita a strati, la crescita continua, il modo di Stranski-Krastanov e il flusso di gradini.

Crescita a strati (o di Frank-van der Merwe)

La superficie è uno degli strati cristallografici del solido, anche se spesso è diverso dai piani cristallini interni: è rilassato (vale a dire, si trova a una distanza dal secondo strato diversa da quella che si stabilisce all'interno della struttura) e può essere ricostruito (ossia può avere una struttura bidimensionale differente). Durante la crescita, su un primo strato se ne deposita un secondo, poi, quando questo è completo o quasi, comincia a formarsene un terzo. Ogni strato si forma a partire da isole bidimensionali che si uniscono (dando luogo a coalescenza). La formazione di tali isole è un processo energeticamente dispendioso, dunque non facile e spesso lento.

Crescita continua (o di Volmer-Weber)

Se la tendenza a stratificare è molto debole, il cristallo cresce formando collinette tipiche della crescita continua che, pur essendo microscopiche, contengono già numerosi atomi e piani cristallini. Hanno spesso la forma di piramidi, prismi o piramidi troncate e, a mano a mano che il cristallo cresce, tendono a mostrare il fenomeno del coarsening, ossia a diventare sempre più larghe, più alte e più spaziate.

Modo di Stranski-Krastanov

Questa modalità di crescita si verifica spesso quando si fa crescere su un substrato cristallino un cristallo di composizione diversa. I primi pochi strati a contatto con il substrato hanno la struttura di quest'ultimo: sono, come si dice, epitassiali. Ciò genera forze elastiche che impediscono un'ulteriore crescita a strati e al di sopra di un certo spessore la crescita diventa continua.

Flusso di gradini

Una superficie tagliata secondo una giacitura che non sia una di quelle definite dalla struttura cristallografica ma si avvicini solamente a una di esse (superficie vicinale) ha la struttura di una scalinata con una ben definita densità di gradini (nel caso più semplice, monoatomici). Durante la crescita, il modo energeticamente più economico e dunque anche particolarmente veloce per aumentare il volume del cristallo è il semplice scorrimento dei gradini nel verso discendente della scalinata.

La stessa superficie può crescere secondo modi diversi alle diverse temperature.

Torniamo ora alla crescita a strati. Già negli anni Trenta del Novecento, Richard Becker e Werner Döring formularono una teoria semplice e convincente di tale processo, di cui discuteremo una formulazione ulteriormente semplificata. A ciascuna delle isole bidimensionali che si formano su uno strato cristallino già depositato si può associare un'energia libera (di Gibbs) che consta essenzialmente di due termini: uno positivo lε che dà il costo della frontiera (l è la lunghezza della frontiera ed ε è il costo energetico per unità di lunghezza del gradino, di altezza h, che costituisce la frontiera) e uno negativo −AhϱΔμ (dove A è l'area dell'isola) che rappresenta il guadagno energetico ottenuto dalla formazione dell'isola. Ogni atomo che solidifica porta a un guadagno Δμ pari alla differenza di potenziale chimico tra il solido e il fluido, mentre il numero di atomi nell'isola è dato dalla densità ϱ moltiplicata per il volume Ah. Poiché l è proporzionale alle dimensioni lineari dell'isola e invece l'area A al loro quadrato, le isole piccole hanno un'energia libera positiva e sono sfavorite mentre le grandi comportano un guadagno energetico. Vi è perciò da superare una barriera, rappresentata dall'energia libera dell'isola più sfavorevole. L'altezza della barriera energetica è chiaramente cε²/Δμ (dove c è una costante geometrica) e la probabilità che sia superata (ossia che il cristallo cresca) è proporzionale al fattore di Boltzmann

[5] formula(

come dimostrò Andrej N. Kolmogorov, la velocità di crescita nei casi più semplici è proporzionale non a questa probabilità ma alla sua radice cubica). Se siamo vicini all'equilibrio (cioè se Δμ è piccolo), la velocità di crescita è esponenzialmente piccola e nessuna crescita a strati dovrebbe essere possibile. In realtà, invece, gli esperimenti dimostrano che la crescita a strati avviene benissimo in queste condizioni e la sua velocità in certi casi è 10³⁰ volte più grande di quella prevista dalla formula di Becker e Döring. Questo paradosso costituì un grave problema per parecchi anni. La teoria di Becker e Döring era sbagliata? L'enigma fu risolto da Frederik C. Frank. La teoria di Becker e Döring era corretta per un cristallo perfetto ma, se nel cristallo è preesistente una dislocazione a vite, la crescita può avvenire con costo energetico minimo avvolgendo a spirale la dislocazione senza bisogno di formare nuove isole. Questa crescita a spirale è di grande importanza quando Δμ è piccolo.

fig. 4

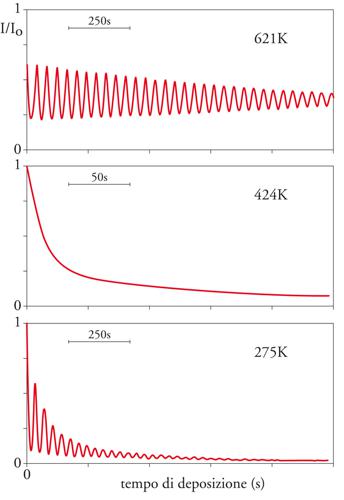
È abbastanza facile scoprire sperimentalmente il modo di crescita. Conviene usare un fascio di particelle quantistiche, riflesse in maniera diffrattiva dalla superficie del cristallo (in particolare, uno dei fasci diffratti è sempre quello speculare, non dipendente dalla periodicità bidimensionale ma solamente dall'ordine). Durante una crescita a strati, si ottiene un fascio speculare intenso quando uno strato è completo e uno molto debole o assente nel caso di massimo disordine, quando lo strato è pieno a metà: si ha dunque un'oscillazione periodica dell'intensità diffratta. Questa oscillazione non c'è nel caso di crescita continua ed è pertanto un'indicazione sicura di crescita a strati. Le particelle usate in questo processo di scattering sono spesso elettroni (RHEED, Reflection high energy electron diffraction), ma possono essere utilizzati anche atomi leggeri. È infatti con lo scattering di atomi di elio che il gruppo di George Comsa ha dimostrato che la crescita del platino (111) è a strati ad alta temperatura (621 K), è continua a temperatura intermedia (424 K) e diventa di nuovo a strati (il modo di crescita a strati rientra) a bassa temperatura (275 K, fig. 4).

Simulazioni di crescita

A causa della complessità dei processi coinvolti (deposizione, diffusione, aggregazione di atomi a isole, coalescenza di isole ed evaporazione) e dei difetti strutturali in superficie (puntuali o estesi), è escluso che si possa modellizzare analiticamente la crescita di un cristallo con una precisione confrontabile con i risultati sperimentali (tranne per quel che riguarda proprietà molto generali, quali la ruvidità o l'evoluzione temporale del livello della superficie, spesso ottenibili, per es., da equazioni differenziali stocastiche). Ciò che non si può ottenere analiticamente può essere realizzato per mezzo di calcoli di simulazione. I metodi di simulazione si possono classificare in due grandi classi: la dinamica molecolare e il metodo Monte Carlo. I metodi di dinamica molecolare sono a loro volta di due tipi, a seconda che si usi la meccanica classica o che si affronti il problema ab initio, tenendo conto della natura quantistica del sistema.

La dinamica molecolare classica in linea di principio è molto semplice: si trattano gli atomi come punti materiali che obbediscono alle equazioni di Newton. Date a un certo istante le posizioni e le velocità degli atomi, si ottengono le accelerazioni dalle forze e queste dall'energia potenziale del sistema, che dipende a sua volta dalle posizioni di tutti gli atomi. Le complicazioni, tuttavia, non mancano. Prima di tutto, anche se si sfrutta la periodicità del cristallo resta inevitabile prendere in considerazione soltanto un numero relativamente piccolo di atomi e bisogna assicurarsi che le proprietà del sistema macroscopico siano ben rappresentate da quelle di tale sistema, relativamente piccolo. L'energia potenziale, inoltre, è una funzione niente affatto ovvia delle posizioni degli atomi. Anche se la dinamica è classica, l'energia potenziale è determinata dalle proprietà quantistiche del solido. Per esempio, nell'importante caso dei metalli ci si è resi conto che un'energia potenziale che descriva abbastanza correttamente le proprietà del sistema può essere solamente non additiva, cioè non può ridursi a una semplice somma di potenziali a due corpi tra coppie di atomi.

La dinamica ab initio è ovviamente molto più complessa. Qui è necessario prendere esplicitamente in considerazione il comportamento degli elettroni, almeno di quelli di valenza (anche se l'enorme rapporto di massa tra nuclei ed elettroni ci consente di postulare che questi ultimi, a norma dell'approssimazione di Born-Oppenheimer, seguano istantaneamente il più lento moto dei nuclei). Fra i metodi di questo tipo ha grande importanza il metodo di Car-Parrinello, che ha permesso per la prima volta di realizzare simulazioni ab initio fisicamente significative. Il metodo Monte Carlo, invece, rinuncia a seguire in dettaglio le leggi della dinamica, sostituendole con un'evoluzione casuale. Il metodo Monte Carlo di equilibrio favorisce, nell'evoluzione casuale, le diminuzioni di energia e cerca così lo stato in cui questa grandezza è minima, quindi l'equilibrio; il metodo Monte Carlo cinetico, invece, cerca di simulare più da vicino l'evoluzione reale del sistema.

Dei due metodi di simulazione indicati, non c'è dubbio che quello della dinamica molecolare sia il più corretto; sembrerebbe dunque che il metodo Monte Carlo non sia interessante. Ma nelle simulazioni di crescita è importante descrivere la deposizione di parecchi strati atomici, durante la quale i singoli atomi sono coinvolti in una miriade di eventi elementari di deposizione, di diffusione, di aggregazione a isole, di coalescenza di isole fra loro e di desorbimento. Simulare tutti questi processi con metodi di dinamica molecolare classica, relativamente lenti, si presenta come un'impresa disperata, anche usando un calcolatore veloce. Conviene ricorrere, allora, al metodo Monte Carlo. È opportuno usare ancora la dinamica molecolare per stabilire con una certa precisione le probabilità degli eventi elementari (in particolare, nel caso dei processi di diffusione, per calcolare le barriere che gli atomi devono superare per poter diffondere). Queste probabilità sono poi introdotte come input in una più vasta simulazione Monte Carlo di crescita. Fra i numerosi lavori che si rifanno a questo procedimento, una collaborazione tra ricercatori italiani e dell'Africa occidentale ha portato a un importante chiarimento del meccanismo di crescita in un caso difficile: quello dell'iridio (110).

Crescita instabile

Gli argomenti precedenti sono ora considerati da un punto di vista globale: invece di partire da un piano, consideriamo un fronte di crescita di forma qualsiasi. Fra queste forme vi è naturalmente il piano, ma in molti casi importanti un fronte planare risulta instabile per cause che possono essere diverse. Tra le cause di tale instabilità la più classica è quella di Mullins-Sekerka, che può essere brevemente descritta come segue. Consideriamo la crescita di un cristallo dal suo fuso: se il cristallo cresce significa che il liquido è sottoraffreddato e dunque si trova a una temperatura più bassa di quella di equilibrio; inoltre, poiché la solidificazione libera calore latente, la temperatura nel liquido scende allontanandosi dal solido. C'è dunque un gradiente di temperatura diretto verso il cristallo in crescita. Se per qualunque ragione il fronte di solidificazione (vale a dire la superficie del cristallo) sviluppa una protuberanza, lo spazio del liquido si riduce, il gradiente di temperatura nel liquido diventa più grande e quindi la solidificazione diventa più intensa: la protuberanza crescerà ancora e il fronte planare sarà dunque instabile. Tale instabilità è contrastata dalla tensione superficiale, che favorisce le superfici piane: essa si oppone fortemente alla formazione di protuberanze locali, ma non di protuberanze estese e dolci, che crescono senza limiti. A riguardo, esiste una lunghezza d'onda critica al di sopra della quale l'instabilità di Mullins-Sekerka ha il sopravvento e distrugge il fronte planare di solidificazione. È invece (parzialmente) stabile un fronte parabolico: la crescita da fuso è ben descritta da un insieme di paraboloidi che crescono nelle varie direzioni, ma che rimangono stabili solamente verso la punta; lateralmente invece sviluppano espansioni secondarie, dando origine a una struttura complessa detta dendrite (dal greco dendrítes, arboreo). È noto che, a causa della struttura microscopica del ghiaccio, nel caso dei cristalli di neve le dendriti sono sei e giacciono in un piano, a 60° l'una dall'altra; una situazione simile si ha anche in altri casi, per esempio per i cristalli di xeno studiati con grande precisione dal fisico svizzero Jörg H. Bilgram e dal suo gruppo, ma in questo caso le dendriti sono soltanto quattro. Il problema della crescita da fuso di un fronte cristallino a forma di paraboloide fu risolto già nel 1947 dal fisico russo G.P. Ivantsov, che calcolò la funzione che lega il numero di Péclet (proporzionale al prodotto del raggio di curvatura ϱ sulla punta del paraboloide per la velocità di crescita v) al disequilibrio. La teoria di Ivantsov è corretta ma incompleta, in quanto non fornisce separatamente i valori di ϱ e v. Ma questo progresso ulteriore è molto difficile da ottenere; si è avuto soltanto in tempi piuttosto recenti e richiede una matematica assai sofisticata, che è stata ben descritta in un libro curato da Claude Godrèche.

Crescita frattale

Abbiamo descritto i modi di crescita caratteristici di un cristallo, ma è opportuno considerare anche la crescita di aggregati meno densi. In particolare, è interessante la crescita di un frattale: in tal caso la densità non soltanto è bassa, ma ‒ quel che più importa ‒ si riduce a mano a mano che l'aggregato cresce. È facile rendersi conto di essere circondati da frattali, non solamente nel mondo effimero che creano i calcolatori, ma anche nel mondo naturale. Un albero è un frattale e (sebbene gli animali al disopra del livello dei celenterati e dei briozoi abbiano poche tendenze frattali) svariati echinodermi come l'Astrospartus mediterraneus ne sono ottimi esemplari; d'altra parte l'intero Universo, con la sua distribuzione di galassie, fra le quali si aprono vuoti sempre più grandi a mano a mano che si esplorano spazi più vasti, si comporta come un frattale.

Una vasta letteratura descrive la crescita frattale. In maggioranza si tratta di simulazioni al calcolatore che si rifanno a un filone inaugurato da Thomas A. Witten e Leonard M. Sander nel 1981, ma che raggiungono sorprendenti risultati di completezza e raffinatezza. Il lavoro di Witten e Sander, in apparenza molto semplice, consisteva in una simulazione nel piano battezzata Diffusion limited aggregation (DLA), in cui a iniziare da un germe si formava un aggregato con la seguente regola: un atomo parte (verso l'interno) dalla circonferenza di un grande cerchio che contiene l'aggregato, compie un percorso a caso nel piano e, se incontra l'aggregato, vi si attacca; se invece incontra di nuovo il grande cerchio esterno, va perduto. L'aspetto interessante della DLA (così chiamata perché l'aggregazione è rallentata dal percorso a caso, che simula un processo diffusivo) è che genera aggregati frattali. Non solo, ma la dimensione frattale (ca. 1,71) di tali aggregati è stata per parecchio tempo un enigma. Una spiegazione soddisfacente di tale dimensione è stata fornita da Luciano Pietronero e collaboratori.

Le corna del cervo

Torniamo a occuparci degli animali. La crescita più inquietante, negli animali superiori e in noi stessi, è il cancro. Non è una crescita di superfici; anzi, forse la differenza più notevole fra la crescita sana, fisiologica, e quella patologica spesso è proprio che la prima è una crescita di superficie: le cellule sane crescono a strati, sono piatte esse stesse e formano tessuti stratificati. Una crescita che ricorda da vicino quella cancerosa, pur essendo perfettamente fisiologica, è invece quella delle corna del cervo. Tutte e quattro le famiglie dei ruminanti avanzati (i Bovidi, gli Antilocapridi, i Cervidi e i Giraffidi) portano corna, ma queste sono molto diverse nelle varie famiglie. Nei Bovidi sono appunto cornee e cave, negli Antilocapridi hanno una sola ramificazione, nei Cervidi sono riccamente ramificate, nei Giraffidi sono rudimentali. Di gran lunga le più interessanti sono le corna dei Cervidi. Walter Modell così le descrive: "Il corno del cervo è un oggetto anatomico unico. La sua crescita, fra quella di tutte le ossa dopo la nascita, è di gran lunga la più veloce. Il mio interesse per questo tessuto insolito risale a quando ero uno studente del secondo anno di medicina: allora cominciai a studiare i cambiamenti stagionali dell'elk (Cervus canadensis) nei laboratori della Società zoologica di New York. Mostrai una delle mie sezioni istologiche di corno in crescita al mio professore, James Ewing, che a quel tempo era lo studioso della crescita dei tumori maligni più importante al mondo. Esaminandolo al microscopio, Ewing descrisse il tessuto, che era straordinariamente ricco di configurazioni mitotiche e dava altri segni di violenta crescita, come un esempio di sarcoma osseo maligno. Quando dissi a Ewing che si trattava in realtà di una sezione di un corno di elk durante una crescita perfettamente normale, mi esortò a continuare lo studio del tessuto, che simulava così bene la crescita cancerosa" (Modell 1969).

È facile capire (grossolanamente) perché corno e cancro si somigliano: entrambi sono tessuti che crescono assai più velocemente degli altri. Ma non è tutto qui: esiste anche una relazione evidente tra velocità di crescita e ramificazione. Aumentando la temperatura o il disequilibrio, gli aggregati che si formano in una simulazione al calcolatore (per es., una doppia DLA, che rappresenta bene gli aggregati lipidici in fase gel che crescono a spese della fase fluida) cambiano forma: con l'aumentare della velocità della crescita diventano sempre più ramificati e, al disopra di una certa temperatura, le ramificazioni diventano casuali. Effetti simili si ottengono se, invece di aumentare la temperatura, si diminuisce l'anisotropia.

bibliografia

Barabási, Stanley 1995: Barabási, Albert-László - Stanley, H. Eugene, Fractal concepts in surface growth, Cambridge, Cambridge University Press, 1995.

Bisang, Bilgram 1995: Bisang, Urs - Bilgram, Jörg H., Shape of the tip and the formation of sidebranches of xenon dend-rites, "Physical review letters", 75, 1995, pp. 3898-3901.

Brener 1992: Brener, Efim e altri, Pattern formation in first-order phase transitions, "International journal of modern physics C", 3, 1992, pp. 825-851.

Burton 1951: Burton, W.K. - Cabrera, Nicolás - Frank, Frederick C., The growth of crystals and the equilibrium structure of their surfaces, "Philosophical transactions of the Royal Society of London, Series A", 243, 1951, pp. 299-358.

Car, Parrinello 1985: Car, Roberto - Parrinello, Michele, Unified approach for molecular dynamics and density-functional theory, "Physical review letters", 55, 1985, pp. 2471-2474.

Caroli 1992: Caroli, Birjis - Caroli, Christiane - Roulet, Bernard, Instabilities of planar solidification fronts, in: Solids far from equilibrium, edited by Claude Godrèche, Cambridge, Cambridge University Press, 1992, pp. 155-296.

Chui, Weeks 1978: Chui, Siu-Tat - Weeks, John D., Dynamics of the roughening transition, "Physical review letters", 40, 1978, pp. 733-736.

Edwards, Wilkinson 1982: Edwards, Sam F. - Wilkinson, David R., The surface statistics of a granular aggregate,"Proceedings of the Royal Society of London, Series A", 381, 1982, pp. 17-31.

Erzan 1995: Erzan, Aişe - Pietronero, Luciano - Vespignani, Alessandro, The fixed-scale transformation approach to fractal growth, "Review of modern physics", 67, 1995, pp. 545-604.

Ferrando 1997: Ferrando, Riccardo - Hontinfinde, Félix - Levi, Andrea C., Morphologies in anisotropic cluster growth: a Monte Carlo study on Ag(110), "Physical review B", 56, 1997, pp. R4406-R4409.

Gallet 1987: Gallet, François - Balibar, Sebastian - Rolley,E_tienne, The roughening transition of crystal surfaces. II. Experiments on static and dynamic properties near the first roughening transition of hcp 4He, "Journal de physique", 48, 1987, pp. 369-377.

Gliozzi 1994: Gliozzi, Alessandra e altri, Temperature and dis-_equilibrium dependence of cluster growth, "Physica A", 203, 1994, pp. 347-358.

Godrèche 1992: Solids far from equilibrium, edited by Claude Godrèche, Cambridge, Cambridge University Press, 1992.

Halpin-Healy, Zhang 1995: Halpin-Healy, Tim - Zhang, Yi-Cheng, Kinetic roughening phenomena, stochastic growth, directed polymers and all that aspects of multidisciplinary stat-istical-mechanics, "Physics reports", 254, 1995, pp. 215-415.

Hontinfinde 2004: Hontinfinde, Félix e altri, Leapfrog induced selective faceting in the growth of missing-row (110) surfaces, "Chemical physics letters", 398, 2004, pp. 50-55.

Hwa 1991: Hwa, Terence - Kardar, Mehran - Paczuski, Maya, Growth-induced roughening of crystalline facets, "Physical review letters", 66, 1991, pp. 441-444.

Kardar 1986: Kardar, Mehran - Parisi, Giorgio - Zhang, Yi-Cheng, Dynamic scaling of growing interfaces, "Physical review letters", 56, 1986, pp. 889-892.

Kunkel 1990: Kunkel, Ralph e altri, Reentrant layer-by-layer growth during molecular-beam epitaxy of metal-on-metal substrates, "Physical review letters", 65, 1990, pp. 733-736.

Levi, Kotrla 1997: Levi, Andrea C. - Kotrla, Miroslav, Theory and simulation of crystal growth, "Journal of physics: condensed matter", 9, 1997, pp. 299-344.

Modell 1969: Modell, Walter, Horns and antlers, "Scientific American", 220, 1969, pp. 114-122.

Ndongmouo Taffoti 2005: Ndongmouo Taffoti, Uguette F. - Hontinfinde, Félix - Ferrando, Riccardo, Numerical study of the stability of (111) and (331) microfacets on Au, Pt, and Ir (110) surfaces, "Physical review B", 72, 2005, pp. 5412-5420.

Nozières, Gallet 1987: Nozières, Philippe - Gallet, François, The roughening transition of crystal surfaces. I. Static and dynamic renormalization theory, crystal shape and facet growth, "Journal de physique", 48, 1987, pp. 353-367.

Pomeau, Ben Amar 1992: Pomeau, Yves - Ben Amar, Martine, Dendritic growth and related topics, in: Solids far from equilibrium, edited by Claude Godrèche, Cambridge, Cambridge University Press, 1992, pp. 365-429.

Tartaglino, Levi 2000: Tartaglino, Ugo - Levi, Andrea C., Dynamic roughening: nucleation and stochastic equations, "Physica A", 277, 2000, pp. 83-105.

Vicsek 1992: Vicsek, Tamás, Fractal growth phenomena, 2. ed., Singapore, World Scientific, 1992.

Villain, Pimpinelli 1995: Villain, Jacques - Pimpinelli, Alberto, Physique de la croissance cristalline, Paris, Eyrolles, 1995.

Witten, Sander 1981: Witten, Thomas A. - Sander, Leonard M., Diffusion-limited aggregation, a kinetic critical phenomenon, "Physical review letters", 47, 1981, pp. 1400-1403.