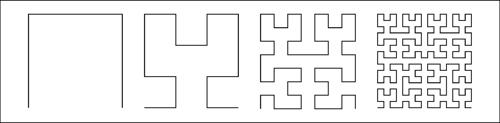
Peano, curva di

Peano, curva di

Peano, curva di particolare curva piana costruita con successive iterazioni che, procedendo all’infinito, riempie un quadrato; essa mostra come sia ambigua la nozione intuitiva di curva come «ente a una dimensione». La sua dimensione di Hausdorff è infatti 2 (→ dimensione frattale). La curva fu presentata da G. Peano per mostrare come la nozione di curva parametrica, se non rafforzata da opportune ipotesi di regolarità, possa condurre a risultati paradossali. L’interesse per questa curva si inserisce nelle ricerche volte a stabilire i legami tra cardinalità e dimensione: la curva di Peano è infatti una curva continua (e quindi un “oggetto monodimensionale”) che tuttavia passa per tutti i punti di un quadrato (e quindi ricopre un “oggetto bidimensionale”). Per la precisione, essa passa due volte per i punti che hanno una coordinata razionale e quattro volte per quelli che hanno entrambe le coordinate razionali. Le funzioni che rappresentano parametricamente tale curva sono continue, ma non derivabili in alcun punto. D’altra parte, mentre un risultato di G. Cantor (si vedano anche i paradossi dell’infinito in → paradosso) mostra che è possibile una corrispondenza biunivoca tra un segmento e un quadrato, è stato dimostrato che è impossibile una corrispondenza biunivoca e bicontinua tra insiemi di dimensioni diverse (→ cardinalità; → corrispondenza biunivoca; → bicontinuità).