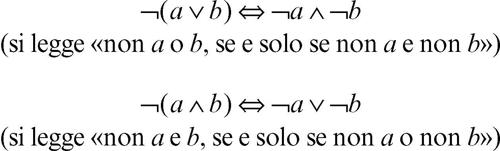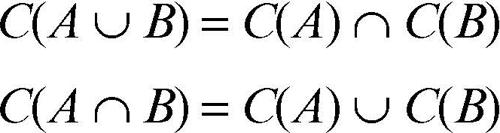De Morgan, leggi di
De Morgan, leggi di
De Morgan, leggi di equivalenze logiche che permettono il passaggio da una congiunzione fra proposizioni a una disgiunzione e viceversa. In simboli:
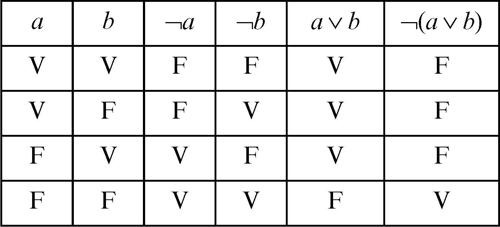
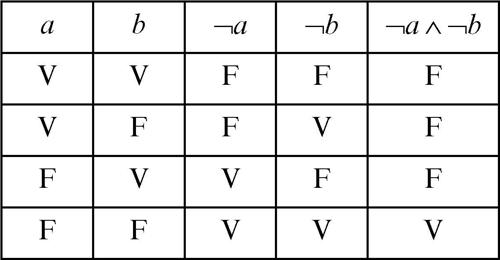
Per esemplificare la prima legge si consideri la domanda: «Questo pomeriggio hai studiato o lavorato?». Rispondere negativamente alla domanda (cioè rispondere «nessuna delle due cose») corrisponde ad affermare che «non ho studiato e non ho lavorato». Ciò si traduce formalmente con la prima legge di De Morgan: la negazione della disgiunzione fra due proposizioni a e b è equivalente alla congiunzione fra le due negazioni. Per la seconda legge, si consideri invece lʼaffermazione «un numero è divisibile per sei», che equivale a dire «il numero in questione è divisibile per due e per tre». Se un numero n non è divisibile per 6, ciò significa che è venuta a mancare almeno una delle due condizioni: «n non è divisibile per 3 oppure n non è divisibile per 2». Ciò è espresso dalla seconda legge di De Morgan: la negazione della congiunzione fra due proposizioni a e b è equivalente alla disgiunzione fra le due negazioni. Si noti che le leggi di De Morgan sono duali nel senso che possono essere ricavate lʼuna dallʼaltra, scambiando il connettivo della congiunzione ∧ con il connettivo della disgiunzione ∨. Le leggi di De Morgan possono essere inoltre verificate tramite le tavole di verità. Per verificare la prima legge si mette a confronto la tavola di verità dellʼenunciato ￢(a ∨ b) con la tavola di verità dellʼenunciato ￢a ∧ ￢b e si nota che i valori di verità risultanti sono gli stessi (si veda lʼultima colonna della tavola di verità di seguito riportata); ciò stabilisce lʼequivalenza logica fra le due proposizioni:
Analogamente, per verificare la seconda legge si mette a confronto la tavola di verità dellʼenunciato ￢(a ∧ b) con la tavola di verità dellʼenunciato ￢a ∨ ￢b e si verifica lʼequivalenza logica fra le due proposizioni.
Le due leggi hanno un corrispettivo nella teoria degli insiemi, che si può illustrare attraverso le seguenti corrispondenze:
• a ogni proposizione a corrisponde un sottoinsieme A di un insieme universo X;
• alla negazione di una proposizione ￢a corrisponde il complementare dellʼinsieme A indicato con C(A);
• alla disgiunzione fra due proposizioni a ∨ b corrisponde lʼunione fra due sottoinsiemi A ∪ B;
• alla congiunzione fra due proposizioni a ∧ b corrisponde lʼintersezione fra due insiemi A ∩ B.
Le leggi di De Morgan possono essere quindi scritte per gli insiemi nel modo seguente:
cioè il complementare dellʼunione di due insiemi è lʼintersezione dei loro rispettivi complementari, mentre il complementare della loro intersezione è lʼunione dei loro rispettivi complementari. Anche per gli insiemi, vale il principio di dualità, ovvero ciascuna delle leggi di de Morgan si può ottenere dallʼaltra scambiando fra loro le operazioni di unione e intersezione.