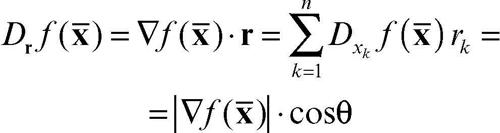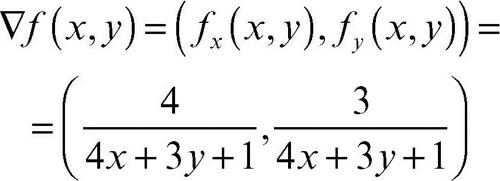derivata direzionale
derivata direzionale
derivata direzionale estensione del concetto di derivata parziale quale derivata di una funzione in n variabili, calcolata lungo una qualsiasi direzione. Data una funzione ƒ(x) di n variabili, cioè con x = (x1, x2, ..., xn), si dice derivata direzionale di ƒ nel punto e nella direzione del versore r ∈ Rn il limite
Il suo significato è analogo a quello della derivata, ma con riferimento ai valori assunti da ƒ sulla retta di equazioni parametriche x = + hr; essa fornisce il coefficiente angolare della sezione dellʼipersuperficie S di equazione y = ƒ(x) con il piano di Rn+1 di equazione x = + hr, che proietta la retta data parallelamente all’asse della variabile dipendente y. Se r è il versore di uno degli assi cartesiani si ha la corrispondente derivata parziale. Per questo la derivata direzionale è vista come generalizzazione della derivata parziale, essendo effettuata non più lungo una direzione parallela agli assi coordinati, come è la derivata parziale, ma lungo una direzione qualsiasi, caratterizzata da un versore.
Se ƒ è una funzione differenziabile in x̄, vale la cosiddetta formula del gradiente:
dove θ è l’angolo tra il vettore gradiente e il versore r. Tale formula traduce il fatto che tutte le tangenti alla ipersuperficie S nel punto giacciono nell’iperpiano tangente. Se ne deduce che la derivata direzionale assume il valore massimo
cioè quando r ha la direzione e il verso del gradiente, minima quando θ = π (stessa direzione e verso opposto) e nulla quando θ = π/2 o θ = 3π/2 (cioè r perpendicolare al gradiente). Per esempio, il gradiente della funzione z = ƒ(x, y) = ln(4x + 3y + 1) è
e dunque nell’origine è (ƒx(0, 0), ƒy(0, 0)) = (4, 3). Preso il versore r = cosφ i + sinφ j nel piano (x, y), la derivata direzionale di ƒ nell’origine e nella direzione di r è dunque 4cosφ + 3sinφ. Essa è massima in corrispondenza dell’angolo φ = arctan(3/4), e vale 5; è nulla per φ = arctan(−4/3). Tuttavia, la validità della formula del gradiente non garantisce da sola la differenziabilità della funzione, come mostra l’esempio della funzione
che, ristretta agli assi cartesiani, è identicamente nulla e che ha tutte le derivate direzionali nulle nellʼorigine; tuttavia non è differenziabile, perché non è continua (il suo limite avvicinandosi allʼorigine lungo la curva di equazione y = x 3 è 1/2 ≠ 0).
Il versore r può essere anche uno dei versori della terna intrinseca a una curva: se r = t si parla di derivata tangenziale, se r = n di derivata normale; analogamente si parla di derivata normale a una superficie. La generalizzazione astratta di questa nozione corrisponde alla cosiddetta derivata di → Gâteaux.