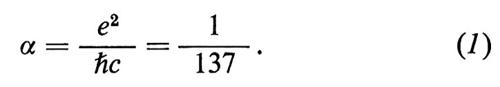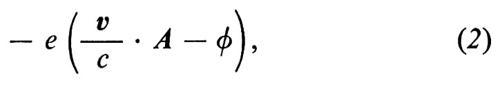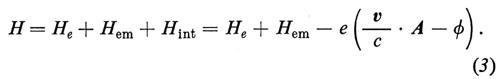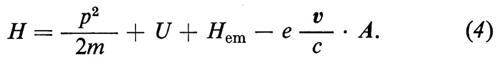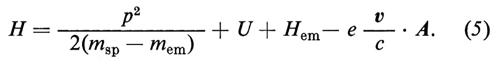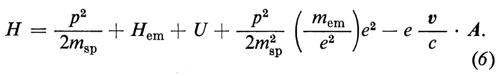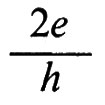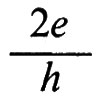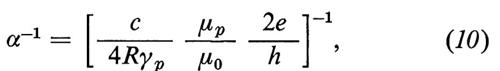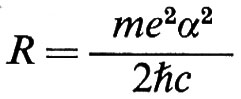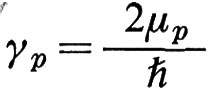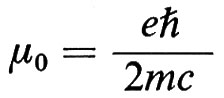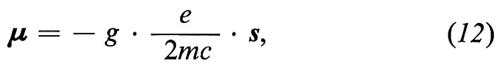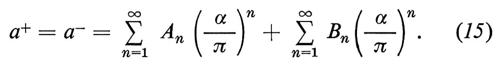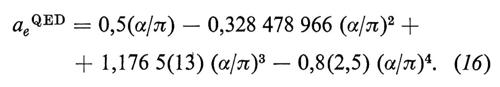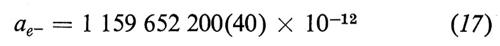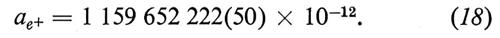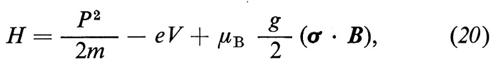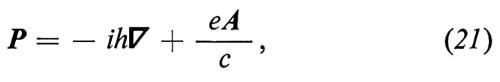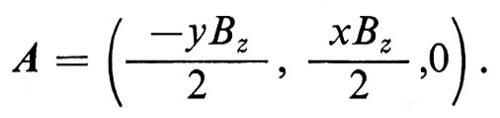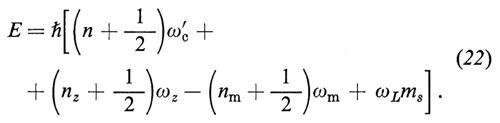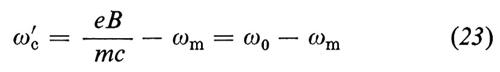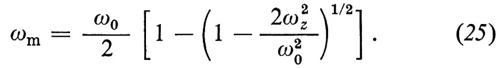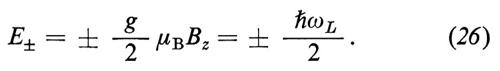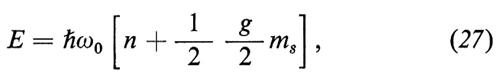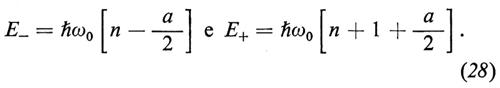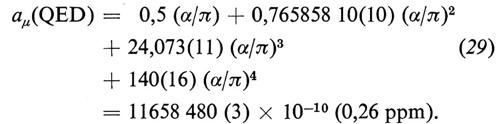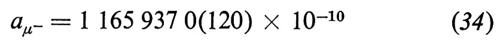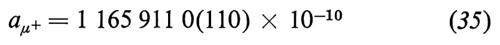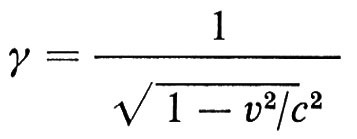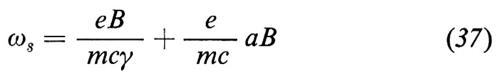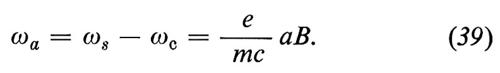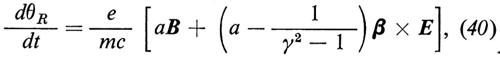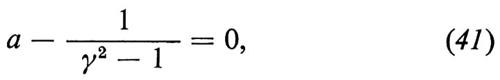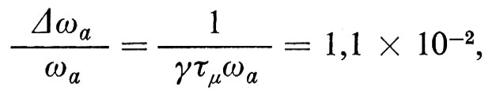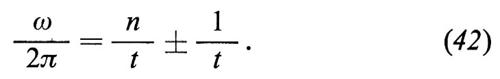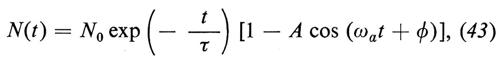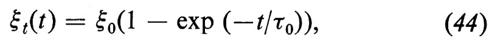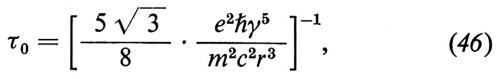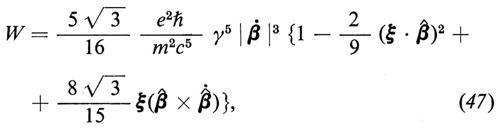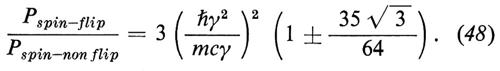Elettrodinamica quantistica
Elettrodinamica quantistica
SOMMARIO: 1. Introduzione. 2. Interpretazione grafica di alcuni processi elettrodinamici. 3 Verifiche sperimentali dell'elettrodinamica: generalità. 4. Verifiche dell'elettrodinamica in sistemi atomici: a) misure della costante di struttura fine indipendenti dalla QED; b) l'effetto Lamb-Retherford dell'atomo di idrogeno; c) il Lamb shift del muonio; d) altre misure fondamentali. 5. I momenti magnetici anomali dei leptoni: a) introduzione; b) considerazioni teoriche; c) l'anomalia dell'elettrone; d) l'anomalia del muone (teoria); e) l'anello di accumulazione di muoni; f) una digressione: la misura della vita media del muone. 6. Verifiche dell'elettrodinamica negli esperimenti di alta energia. 7. Polarizzazione dei fasci di elettroni e positoni negli anelli di accumulazione. 8. Conclusioni. □ Bibliografia.
1. Introduzione
L'elettrodinamica quantistica (QED, dall'inglese Quantum Electro-Dynamics) è una teoria che descrive l'interazione tra gli elettroni, i positoni e i fotoni ed è in eccellente accordo con i risultati sperimentali.
Le equazioni dell'elettrodinamica quantistica erano già note verso la fine degli anni venti. La teoria era stata formulata nei lavori classici di Dirac (v., 1927), Heisenberg e Pauli (v., 1929), Fermi (v., 1930) e Heisenberg (v., 1934). Un metodo per risolvere queste equazioni consisteva nello sviluppare le funzioni d'onda che rappresentano le grandezze fisiche in serie di potenze della costante di struttura fine
Purtroppo l'applicazione del metodo perturbativo alla soluzione dei problemi dell'elettrodinamica non era soddisfacente. La situazione in cui si trovava l'elettrodinamica in quegli anni può riassumersi essenzialmente nel modo seguente: tutte le volte che si proseguiva nello sviluppo in serie delle grandezze fisiche in esame, la regola pratica, che si insegnava agli studenti, era di arrestarsi appena si trovava un valore diverso da zero. Se si osava andare avanti, l'approssimazione seguente, in genere, era divergente.
Questa situazione non era affatto soddisfacente. Si cercò di migliorare la teoria introducendo ‛fattori di forma' di vario tipo, che permettessero di ‛tagliare via' le divergenze che davano risultati infiniti, non corrispondenti, evidentemente, alla realtà. Questa tecnica non dette i risultati che i suoi autori si aspettavano e fu così abbandonata.
Nonostante questa situazione insoddisfacente, era chiaro che le equazioni di base della teoria davano risultati corretti in prima approssimazione. Occorreva, pertanto, trovare il modo di evitare le espressioni divergenti, dovute alle correzioni radiative, che erano introdotte dai termini di ordine superiore al primo nella teoria perturbativa. Questa regolarizzazione della teoria fu ottenuta mediante la tecnica della rinormalizzazione (v. Bethe, 1947).
Per illustrare il ragionamento alla base di questa tecnica è necessario addentrarsi un po' nel formalismo teorico. Consideriamo un campo elettromagnetico in presenza di un elettrone. L'hamiltoniana di un tale sistema si può scrivere come la somma di tre termini: l'hamiltoniana He dell'elettrone isolato, come se il campo elettromagnetico non ci fosse, l'hamiltoniana Hem del campo elettromagnetico, come se l'elettrone non ci fosse, e un termine di interazione Hint, proporzionale alla carica e dell'elettrone, la cui forma è
in cui v è la velocità dell'elettrone e A e ϕ i potenziali vettore e scalare del campo elettromagnetico nella posizione occupata dall'elettrone. L'hamiltoniana totale del sistema ‛campo elettromagnetico più elettrone' è quindi
Il problema fondamentale della dinamica del nostro sistema è quello di risolvere l'equazione di Schrödinger la cui hamiltoniana è data dalla (3). Consideriamo per semplicità il caso non relativistico, in cui l'elettrone si muove con velocità piccole rispetto alla velocità della luce. L'approssimazione che si utilizza nel risolvere l'equazione di Schrödinger consiste nel considerare He + Hem come la parte imperturbata del sistema e Hint come la perturbazione. In questa trattazione il problema ‛non perturbato' è molto semplice, poiché il campo elettromagnetico non è influenzato dall'elettrone e viceversa. Il termine He è l'energia dell'elettrone ed è la somma della sua energia cinetica, che si scrive, nel caso non relativistico, p2/2m, p essendo la quantità di moto, e della sua energia potenziale U. Hem è l'energia del campo elettromagnetico e Hint si riduce, nel caso di radiazione pura, a (e/c)v • A. L'energia del sistema si può scrivere
Se si studia, applicando i metodi soliti della teoria delle perturbazioni, lo spostamento dei livelli energetici dello spettro dell'atomo di idrogeno, dovuto alla perturbazione (e/c)v • A, si trova che, in prima approssimazione, il risultato è nullo e, in seconda approssimazione, il risultato diverge. Questo vuol dire che il primo termine dello sviluppo, quello proporzionale a e, ha un coefficiente nullo; il secondo termine, che è proporzionale a e2, ha un coefficiente infinito.
Il risultato sperimentale della misura dello spettro di struttura fine dell'atomo di idrogeno non poteva essere in accordo con il calcolo perturbativo sopra menzionato.
L'idea di Bethe (v., 1947), o più esattamente l'idea che fu discussa in una conferenza alla quale parteciparono una trentina di fisici teorici, fu quella di chiedersi quale fosse il valore della massa m da sostituire nell'espressione p2/2m. L'idea di poter scrivere l'hamiltoniana come somma di tre termini si fonda sull'ipotesi che si possano separare tra loro le quantità relative al solo elettrone, al solo campo elettromagnetico e al termine di interazione. In questo caso la quantità p2/2m deve riferirsi al solo elettrone e la massa m è la massa meccanica dell'elettrone, cioè il valore della massa dell'elettrone quando non è in presenza del campo elettromagnetico. Nel fare i calcoli si sostituisce a m il valore sperimentale msp = mem + m, il che non è corretto. L'equazione (4) va riscritta
La massa elettromagnetica è un effetto del secondo ordine, poiché si manifesta quando il campo interagisce con l'elettrone, ed è quindi proporzionale a e2. Si può riscrivere la (5) nel modo seguente:
Scrivendo l'hamiltoniana secondo la (6) si mette bene in evidenza l'esistenza di due perturbazioni, di cui una, cioè (e/c)v • A, dà un risultato nullo al primo ordine e un risultato infinito al secondo ordine e l'altra, cioè p2/2m²sp • (mem/e2)e2, dà luogo anch'essa a un termine infinito. Il punto essenziale dell'osservazione di Bethe è che le due parti infinite si cancellano e resta un risultato finito che, nel caso della struttura fine dell'atomo di idrogeno, è molto vicino al risultato sperimentale.
La formulazione teorica di Bethe non è invariante per trasformazioni di Lorentz, cioè è un calcolo non relativistico e come tale è destinato a predire risultati non corretti quando si arriva a energie dell'ordine di mspc2. I lavori successivi di Tomonaga (v., 1948), Schwinger (v., 1948), Feynman (v., 1949) e Dyson (v., 1949) hanno permesso di sviluppare uno schema teorico estremamente elegante che ha esteso l'idea di Bethe al caso relativistico e, quindi, ha permesso di interpretare e predire con successo i fenomeni fisici dell'elettrodinamica a qualsiasi energia.
L'estensione della teoria della rinormalizzazione al regime di moto relativistico ha costituito un arduo problema matematico. Nell'estendere la teoria dell'elettrodinamica quantistica al caso relativistico si introducono operatori di campo che rappresentano le operazioni di distruzione e di creazione di un fotone, di un elettrone e di un positone. È estremamente importante attirare l'attenzione del lettore sul fatto che l'elettrodinamica ammette l'esistenza di uno stato fisico che rappresenta il ‛vuoto'. Se si applicano gli operatori di creazione allo stato di vuoto, si generano nuovi stati che contengono un qualsiasi numero assegnato di elettroni, positoni e fotoni con valori della quantità di moto e del momento angolare intrinseco (spin) definiti a priori.
Il vuoto è lo stato del sistema che possiede il valore minimo del tetravettore energia-quantità di moto ed è invariante per trasformazioni di Lorentz, cioè, se si cambia il sistema di riferimento, lo stato di vuoto non cambia. Applicando gli operatori di creazione al vuoto si può generare lo stato in cui è creata una particella, lo stato in cui sono create due particelle e così via, di modo che lo spazio (di Hilbert) che si costruisce è molto simile, alla fine, al nostro universo.
La teoria dei campi, e in particolare la QED, insegna che il vuoto è in realtà molto complicato. Esso è simile a un sistema dinamico di spin nullo, il cui tetravettore energia-quantità di moto tende ad avere anch'esso un valore nullo. Come un campo di spin 0, il vuoto può avere numeri quantici quali lo spin isotopico, la parità, la stranezza e così via.
2. Interpretazione grafica di alcuni processi elettrodinamici
Lo scopo dell'elettrodinamica è quello di calcolare la probabilità che una configurazione fisica iniziale evolva in una configurazione finale. La teoria elettrodinamica permette di costruire un operatore, la matrice S, i cui termini danno la probabilità che uno stato iniziale evolva in uno stato finale assegnato.
I vari termini della serie perturbativa possono essere rappresentati graficamente in modo molto suggestivo. La rappresentazione grafica è dovuta a Feynman. L'n-esimo termine della serie perturbativa rappresenta n interazioni successive tra il campo elettromagnetico, che soddisfa le equazioni di Maxwell, e quello dell'elettrone, che soddisfa l'equazione di Dirac. Il diagramma contiene n-vertici in ognuno dei quali ha luogo l'interazione tra elettroni, fotoni, positoni. A ciascun vertice si possono applicare, per esempio, le seguenti operazioni: a) la creazione o la distruzione di un fotone; b) la creazione di un elettrone o l'annichilazione di un positone; c) l'annichilazione di un elettrone o la creazione di un positone.
La fig. 1 rappresenta i termini del secondo ordine (n = 2) della serie perturbativa della matrice S. Il primo diagramma (I) rappresenta l'interazione tra un elettrone e un fotone, cioè l'effetto Compton. Le linee ondulate rappresentano i fotoni, le linee continue gli elettroni e i positoni. Il simbolo k rappresenta il tetravettore energia-quantità di moto del fotone, mentre q e p rappresentano i tetravettori energia-quantità di moto rispettivamente dell'elettrone e del positone. Le frecce indicano creazione se puntano lontano dal vertice e annichilazione se puntano verso il vertice.
Il secondo diagramma (II) rappresenta l'interazione elettrone-elettrone. Il terzo diagramma (III) rappresenta la produzione di coppie di fotoni a causa dell'annichilazione di una coppia elettrone-positone. Il quarto diagramma (IV) rappresenta la produzione di una coppia elettrone-positone a causa dell'interazione fotone-fotone. Il quinto diagramma (V) indica il processo di interazione di un elettrone (o di un positone) con il campo di radiazione originato dalla carica stessa, cioè descrive l'interazione tra un elettrone e il suo campo di radiazione. Il sesto diagramma (VI) descrive la creazione e la distruzione successiva di una coppia virtuale di elettroni e positoni da parte di un fotone. L'ultimo diagramma (VII) rappresenta la creazione e la successiva annichilazione di una coppia virtuale di elettroni e positoni da parte di un fotone anch'esso in uno stato virtuale, cioè in uno stato in cui la quantità di moto, l'energia e la massa dell'elettrone e del fotone (mγ = 0) non soddisfano le ben note relazioni della meccanica relativistica (v. McConnell, 1958).
I diagrammi V, VI e VII sono responsabili delle ben note divergenze in elettrodinamica quantistica, brevemente menzionate nel cap. 1. L'eliminazione di queste divergenze è stata ottenuta con la teoria della rinormalizzazione della massa m e della carica e dei quanti del campo di Dirac.
La nube di fotoni virtuali (diagramma V) che accompagna un elettrone aumenta l'energia dell'elettrone; si può interpretare questo aumento di energia come un aumento della massa dell'elettrone. La massa m dell'elettrone libero, non sottoposto ad alcuna interazione, non coincide, quindi, con la massa sperimentale dell'elettrone: è la massa di un elettrone fittizio. La massa reale msp è la somma della massa m dell'elettrone libero, fittizio, e della massa della nube dei fotoni che rappresentano l'azione del campo elettromagnetico. Questi fotoni, come si può vedere dal diagramma V, vengono emessi e riassorbiti dall'elettrone nel processo di interazione. La massa msp è quindi
msp = m + mem. (7)
La tecnica che permette di regolarizzare le divergenze provenienti dal termine mem consiste nell'attribuire il valore − ∞ a m e nell'imporre che msp sia uguale al valore sperimentale della massa dell'elettrone.
Una procedura simile si applica ai diagrammi VI e VII che danno luogo alle divergenze della carica elettrica. La quantità e1 è una correzione, il cui valore è infinito, della carica e dell'elettrone libero. Come nel caso della massa, si assume e = − ∞, in modo che sia
e + e1 = esp, (8)
dove esp indica il valore sperimentale della carica dell'elettrone. Questa procedura dà la rinormalizzazione della carica.
Una conseguenza importante della QED è che una particella carica può emettere e assorbire fotoni anche in assenza di un campo elettromagnetico esterno, si hanno cioè le cosiddette ‛fluttuazioni del vuoto'. Esse hanno importanti conseguenze sperimentali, tra cui: l'emissione spontanea della radiazione da parte di un atomo eccitato, lo spostamento dei livelli energetici dell'atomo di idrogeno (Lamb shift) e, infine, l'esistenza di una correzione ‛radiativa' del momento magnetico dell'elettrone e del muone (v. capp. 4 e 5).
3. Verifiche sperimentali dell'elettrodinamica: generalità
L'elettrodinamica quantistica descrive un'enorme quantità di fenomeni fisici e ha permesso ai fisici di scoprire fenomeni che sono alla base di realizzazioni tecniche di grande importanza (basti pensare al maser e al laser). Essa non è ancora nella sua forma definitiva, poiché la sua formulazione dà luogo a divergenze che si eliminano con la teoria della rinormalizzazione, la quale può essere considerata, più che una vera e propria teoria, un procedimento ad hoc per evitare gli infiniti. In questa situazione è estremamente importante verificare la teoria, cioè le regole matematiche che interpretano e predicono i fenomeni fisici.
Gli esperimenti sono tra i più brillanti della fisica. Le precisioni raggiunte hanno quasi dell'incredibile. Le quantità che si misurano sono legate tra loro, cioè sono espresse in funzione di costanti fondamentali, quali le masse, i momenti magnetici, la costante di struttura fine, le transizioni di struttura iperfine, ecc., in modo da costituire un intreccio di correlazioni tra molte grandezze fondamentali.
Un ruolo importante nelle verifiche sperimentali dell'elettrodinamica spetta al muone. Questo ruolo è dovuto al fatto che il muone ha la stessa carica dell'elettrone e, come quest'ultimo, non è soggetto alle interazioni nucleari forti. Nella tab. I sono riportati i valori delle proprietà fisiche più importanti dell'elettrone, del muone e del fotone.
Nel descrivere brevemente alcuni degli esperimenti dell'elettrodinamica ci soffermeremo più sui principi su cui si basano che sui dettagli tecnici.
Gli esperimenti descritti si possono dividere in due classi: i primi verificano le correzioni radiative di ordine superiore al primo, in cui la teoria della rinormalizzazione ha un ruolo dominante; i secondi verificano l'elettrodinamica quantistica in situazioni particolari, dove, per esempio, il momento trasferito nel processo di interazione tra elettroni e positoni possiede valori molto grandi.
Gli esperimenti del primo tipo sono, generalmente, esperimenti di grande precisione. Per esempio le esperienze di fisica atomica e le misure dei momenti magnetici anomali dei leptoni danno la scala della precisione necessaria per verificare i contributi dovuti alle correzioni radiative. Gli esperimenti del secondo tipo costituiscono le verifiche che si fanno ad alta energia, per esempio negli anelli di collisione elettrone-positone. Da tutte queste esperienze l'elettrodinamica risulta verificata con grande precisione.
4. Verifiche dell'elettrodinamica in sistemi atomici.
a) Misure della costante di struttura fine indipendenti dalla QED.
Il confronto tra la teoria elettrodinamica e l'esperienza è possibile solo se si conosce bene il valore della costante di struttura fine. Ci sono almeno due strade per misurare con grande precisione la costante di struttura fine, α = e2/ℏc = 1/137.
1. I valori sperimentali che si ottengono negli esperimenti ideati per verificare la QED si confrontano con la teoria. Poiché α interviene in questo confronto, si determina il valore di α per cui la teoria e l'esperienza sono in accordo. Tutti i valori di α così ottenuti devono coincidere, se la teoria è in accordo con l'esperienza.
2. Il valore di α si ottiene da esperienze che non dipendono, a stretto rigore, dall'elettrodinamica quantistica, o più esattamente che non hanno nulla a che fare con le correzioni radiative della teoria.
La più recente misura di a, che appartiene a questa seconda classe, è quella di Olsen e Williams (v., 1979). L'esperienza consiste nel misurare il rapporto giromagnetico del protone e l'effetto Josephson, che consiste nello scambio di coppie di elettroni tra due superconduttori separati da un materiale isolante. Si ottiene uno dei valori più precisi del rapporto
Formula = 483,5912(30)
MHz/μV (6 ppm). (9)
Per ottenere α, oltre la quantità Formula
occorre misurare un'altra grandezza fondamentale a essa legata. La scelta migliore è suggerita dalla relazione
Formula
essendo Formula
la costante di Rydberg, Formula
il rapporto giromagnetico del protone e Formula
il momento magnetico dell'elettrone. Tutte queste quantità sono misurate con una precisione di 0,1 ppm. Si ottiene così
α-1 = 137,035963(15) (0,11 ppm). (11)
(Il numero tra parentesi è l'errore quadratico medio).
Recentemente la costante di struttura fine è stata misurata da von Klitzing e altri (v., 1980) facendo uso dell'effetto Hall quantistico. La resistenza di Hall, nei conduttori quasi bidimensionali che si possono ottenere alle interfacce dei semiconduttori, assume valori che sono sottomultipli interi della grandezza fondamentale h/e2.
La precisione della misura di α ottenuta con questo metodo dipende in pratica dal rapporto e2/h, poiché la velocità della luce è nota da misure astronomiche e spettroscopiche con altissima precisione. Il valore più accurato finora ottenuto con questo metodo è stato ricavato da Tsui e altri (v., 1982) ed è
α-1 = 137,035968 ± 0,000023.
b) L'effetto Lamb-Retherford dell'atomo di idrogeno.
Nella fig. 2 è mostrato lo spettro di struttura fine e iperfine dell'atomo di idrogeno nei casi in cui i numeri quantici principali siano n = 1 e n = 2.
La soluzione dell'equazione di Schrödinger per l'elettrone in un atomo di idrogeno fornisce i seguenti stati legati:
1S1/2; 2S1/2 2P1/2 2P3/2; 3S1/2 3P1/2 3P3/2 3D3/2 3D5/2; ... .
Ciascuno di questi stati del sistema è specificato dal numero quantico principale n = 1, 2, 3 ..., dal momento angolare orbitale l = 0(S), = 1(P), = 2(D), ..., = n − 1 e dal momento angolare totale j = 1/2, 3/2, 5/2. Tutti gli stati con lo stesso valore di n sono degeneri, cioè sono caratterizzati da uno stesso autovalore dell'energia. Risolvendo invece lo stesso problema con l'equazione di Dirac, a causa degli effetti relativistici, principalmente dovuti all'accoppiamento dello spin con il moto orbitale (spin-orbit coupling), i termini con n fisso si dividono in n componenti di struttura fine:
1S1/2; 2S1/2 2P1/2, 2P3/2; 3S1/2 3P1/2, 3P3/2 3D3/2, 3D5/2; ... .
Per esempio, lo stato 2P3/2 risulta possedere un'energia maggiore degli stati, ancora degeneri, 2S1/2 e 2P1/2.
Se si tiene conto, nell'approssimazione relativistica, anche del moto relativo dell'elettrone e del protone, il sistema è descritto dall'equazione di Bethe-Salpeter (v. Bethe e Salpeter, 1957). Se infine si tiene conto anche della struttura del protone, allora tutti i livelli energetici dell'atomo di idrogeno sono separati, cioè il sistema non è più degenere.
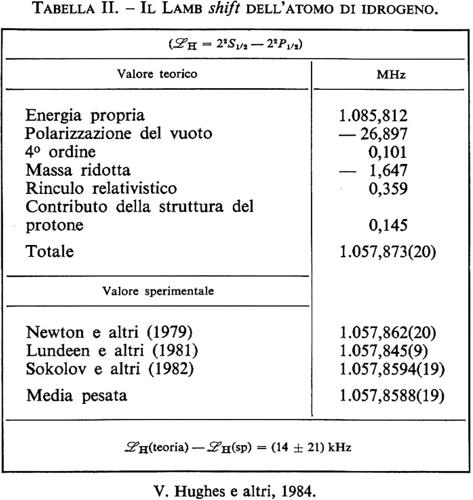
Le correzioni radiative contribuiscono alla separazione dei livelli energetici per circa lo 0,1%, cioè 1.000 ppm. Il contributo dominante nella separazione dei livelli energetici dell'atomo di idrogeno nella serie di struttura fine e iperfine deriva dall'interazione di un campo elettromagnetico esterno (all'atomo di idrogeno) con il momento magnetico anomalo dell'elettrone. Gli altri contributi sono trascurabili rispetto a questo, infatti essi sono dell'ordine di 1,2 ppm, nel caso della struttura fine, e di circa 60 ppm, nel caso della struttura iperfine.
Il Lamb shift è dovuto totalmente alle correzioni radiative di ordine superiore al primo nella serie perturbativa della matrice S. La misura del Lamb shift fu di grande importanza per lo sviluppo dell'elettrodinamica quantistica. L'esperienza, eseguita nel 1947 da Lamb e Retherford, mostrò una significativa deviazione dai risultati della teoria di Dirac. Risultò infatti una differenza di energia di circa 1.000 MHz fra i livelli 2S1/2 e 2P1/2, che invece, secondo la teoria relativistica dell'elettrone, dovrebbero avere la stessa energia. Nello stesso anno Bethe (v., 1947) interpretò questa discrepanza attribuendola all'effetto del campo elettromagnetico originato dall'elettrone stesso. L'accordo tra il valore sperimentale di Lamb e Retherford e quello teorico di Bethe era impressionante, nonostante che il calcolo fosse stato fatto nell'approssimazione non relativistica. L'esperimento richiamò l'attenzione su un problema di grande importanza, quello delle correzioni radiative. Nell'intento di risolvere questo problema Bethe pose le basi della teoria della rinormalizzazione.
Numerose misure del Lamb shift sono state effettuate dal 1947 fino ai nostri giorni. Nella tab. II sono riportati alcuni dei valori sperimentali del Lamb shift.
c) Il Lamb shift del muonio.
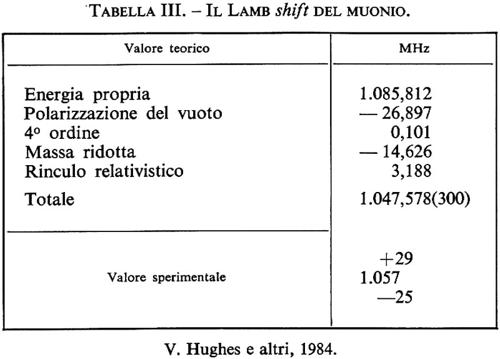
Il muonio è un atomo (v. ATOMO) in cui un elettrone ruota attorno a un muone di carica elettrica positiva. Si tratta di un sistema simile all'atomo di idrogeno, in cui il protone è sostituito da un muone positivo. È un sistema ideale per verificare la teoria elettrodinamica, poiché il muone, come l'elettrone, non ha una struttura interna, mentre il protone ha una struttura interna complessa che rende impossibile l'interpretazione degli esperimenti puramente in termini di QED.
Le misure della struttura iperfine e dell'effetto Zeeman nello stato fondamentale (n = 1) hanno fornito verifiche molto precise della QED e hanno permesso di misurare la costante di struttura fine α e il rapporto dei momenti magnetici del muone e del protone con grande precisione (v. Hughes e Kinoshita, 1977). Va ricordato (v. tab. II) che la struttura del protone contribuisce al Lamb shft per 145 kHz, cioè per 1,4 parti in 104. Nel caso del muonio i contributi teorici al Lamb shift sono formalmente gli stessi di quelli dell'atomo di idrogeno, escluso il termine dovuto al fattore di forma del protone. Nella tab. III sono riportati i contributi nel caso del muonio. Il valore sperimentale è in ottimo accordo con il valore teorico. Esperimenti più accurati sono previsti in un prossimo futuro.
d) Altre misure fondamentali.
Una rassegna dettagliata delle verifiche dell'elettrodinamica deve accennare, oltre che alle misure della struttura iperfine dell'atomo di idrogeno e del muonio, anche alla misura della struttura fine dello stato fondamentale del positonio. Anche questo, come il muonio, è un sistema particolarmente adatto per verificare sperimentalmente la validità dell'elettrodinamica poiché i suoi costituenti non hanno interazioni nucleari forti. Il positonio è infatti un atomo in cui un elettrone e un positone ruotano l'uno attorno all'altro. Quando un positone urta contro un atomo e cattura uno degli elettroni che descrive un'orbita attorno al nucleo, si forma un positonio. La vita media del positonio dipende dallo stato in cui si trova e varia da 1,4 × 10-7 s per l'ortopositonio, in cui gli spins dell'elettrone e del positone sono paralleli tra loro, a 1,25 × 10-10 s per il parapositonio, in cui gli spins sono antiparalleli. Le misure di struttura fine concordano con i grafici del secondo ordine in α e costituiscono quindi verifiche precise ed eleganti dell'elettrodinamica.
Le misure della struttura iperfine dell'atomo di idrogeno sono tra le più precise di tutta la fisica. L'effetto dell'elettrodinamica è però mascherato dalla struttura del protone, che rende difficile il confronto accurato tra la teoria e il valore sperimentale. L'effetto del fattore di forma del protone è purtroppo dominante rispetto alle correzioni radiative. La struttura iperfine del muonio, nello stato fondamentale, è esente da effetti nucleari e i contributi dell'elettrodinamica sono più importanti (circa 200 ppm) e costituiscono quindi una buona verifica della teoria.
Per ulteriori dettagli su questi esperimenti si rinvia alla letteratura specializzata (v. Hughes e Kinoshita, 1977).
5. I momenti magnetici anomali dei leptoni.
a) Introduzione.
Le misure dei momenti magnetici dell'elettrone e del muone hanno avuto un ruolo di primo piano nello sviluppo dell'elettrodinamica (v. Combley e Picasso, 1980).
Il rapporto giromagnetico g è definito dalla seguente relazione
dove μ è il momento di dipolo magnetico, e la carica del leptone (elettrone o muone) e m la sua massa, e s è lo spin o momento angolare intrinseco. Il numero adimensionale g è una proprietà fondamentale della particella e delle sue interazioni. Nel caso di una sfera rigida in rotazione, la cui carica elettrica e la cui massa abbiano la stessa distribuzione spaziale, con un semplice calcolo di meccanica classica si trova g = 1.
Quando si interpreta l'equazione (12) secondo la meccanica quantistica, essa rappresenta una relazione tra gli operatori μ e s. La quantità g misura allora la deviazione del momento magnetico della particella dal valore classico unitario. Per esempio il valore sperimentale di g del protone è 5,586, mentre per l'elettrone e il muone si ha g = 2,002. Il valore di g del protone non può essere calcolato nell'ambito della teoria elettrodinamica, poiché è dovuto alle correnti delle cariche (i quarks) che costituiscono la struttura complessa del protone. Il valore di g dell'elettrone e del muone può essere predetto con grande precisione dalla QED e questo fatto indica che i leptoni carichi non hanno una struttura complicata come il protone. Possiamo quindi affermare che il rapporto giromagnetico g del protone riflette la dinamica interna della particella, mentre per i leptoni è il risultato dell'interazione tra la carica e il campo di radiazione.
La teoria di Dirac predice il valore g = 2 per il rapporto giromagnetico dell'elettrone (o del muone).
Le misure accurate delle strutture iperfini degli atomi di idrogeno e di deuterio fatte da Nafe, Nelson e Rabi (v., 1947) all'inizio del 1947 erano in disaccordo con questa predizione. Breit (v., 1947) suggerì che la discrepanza tra i risultati sperimentali e i calcoli teorici sarebbe scomparsa se si fosse ammesso che il rapporto giromagnetico avesse un valore diverso da 2, una piccola differenza dell'ordine dell' 1‰. Schwinger (v., 1948) calcolò questo valore e trovò che la deviazione dal valore 2 era dovuta a un fenomeno radiativo del primo ordine, cioè all'emissione di un fotone virtuale e all'assorbimento dello stesso da parte dell'elettrone che interagisce con il campo magnetico esterno. Il risultato di Schwinger è
g = 2(1 + α/2π). (13)
Il valore ricavato da Kusch e Foley (v., 1947) nel dicembre del 1947 era in accordo con il valore teorico. Il risultato sperimentale è g = 2(1 + 0,00119(5)) con un errore relativo di 25 ppm. La storia delle misure del momento magnetico dell'elettrone e poi del muone è uno dei capitoli più belli della fisica sperimentale.
b) Considerazioni teoriche.
Come si è ricordato sopra, a causa delle correzioni radiative, il fattore g dell'elettrone (o del muone) ha un valore leggermente diverso dal valore di Dirac
μ = − 2(1 + a) μ0s, (14)
dove a = (g − 2)/2 indica la cosiddetta anomalia del momento magnetico. Nella teoria elettrodinamica l'anomalia è espressa in serie di potenze della costante di struttura fine:
I coefficienti An non dipendono dalla massa dell'elettrone (o del muone) e quindi sono gli stessi sia per l'elettrone che per il muone. I termini in Bn sono funzioni del rapporto mμ/me. Quello che è interessante è che tutti i termini in An, a qualunque ordine, contribuiscono con lo stesso valore al momento magnetico anomalo sia dell'elettrone che del muone (nonché del leptone τ, recentemente scoperto a SLAC). I termini in Bn sono diversi nei tre casi (il momento magnetico anomalo del τ non è stato ancora misurato). Nel caso dell'elettrone si trascurano i termini in Bn, poiché sono dell'ordine di 3 × 10-12. Si noti che non si può calcolare l'anomalia del muone senza calcolare i contributi che provengono dall'elettrone.
Nella fig. 3 sono riportati i diagrammi di Feynman del secondo ordine in α del muone e dell'elettrone e nella fig. 4 quelli del terzo ordine in α. In α3 sono 72 i diagrammi comuni all'elettrone e al muone, cioè i termini che non dipendono dalla massa. Se si pensa che ognuno di questi grafici rappresenta un lungo calcolo, ci si può rendere conto dell'enorme lavoro fatto dai fisici teorici per calcolare tutti questi termini.
c) L'anomalia dell'elettrone.
Il valore teorico dell'anomalia dell'elettrone è
I numeri tra parentesi indicano l'incertezza nel calcolo dei coefficienti An e Bn. L'espressione è del quarto ordine in α, cioè dell'ottavo nella carica elettrica.
Il valore sperimentale ottenuto da Dehlmet e altri (v., 1981) è
I due risultati si riferiscono all'elettrone e al positone e mostrano che l'anomalia ha lo stesso valore per la particella e per l'antiparticella (verifica del teorema CPT).
Il valore teorico è
ae = 1 159 652 460(75) (127) × 10-12. (19)
La prima parentesi dà l'errore teorico, dovuto alle approssimazioni fatte, e la seconda l'errore dovuto alla misura sperimentale di α. La differenza tra il valore teorico e il valore sperimentale è
Δae = aesp − aet = − 251(154) × 10-12.
Per misurare il rapporto giromagnetico g dei leptoni si utilizzano generalmente due metodi. In entrambi i metodi i leptoni (elettroni e muoni) sono sottoposti all'azione di un campo magnetico statico, di modo che si origina un'interazione tra il momento magnetico del leptone e il campo magnetico esterno. In un caso si misura direttamente la precessione dello spin nel campo magnetico, nell'altro si induce una transizione tra due livelli di energia del leptone nel campo magnetico. Questa transizione è indotta dall'esterno, applicando un campo elettromagnetico oscillante. Il primo metodo si chiama ‛metodo di precessione', il secondo ‛metodo di risonanza'. Nel primo si misura direttamente la variazione dello stato di polarizzazione del sistema in funzione del tempo, nel secondo si misurano le frequenze di transizione tra due stati quantici del sistema.
La misura più recente e più precisa del momento magnetico anomalo dell'elettrone è stata fatta impiegando la tecnica della risonanza magnetica; la misura dell'anomalia del muone è stata fatta impiegando la tecnica della precessione.
Nel caso dell'elettrone, esso viene intrappolato in un campo magnetico omogeneo. Il campo elettromagnetico che costituisce la ‛trappola' non deve perturbare troppo lo stato fisico del sistema, in modo che si possa estrarne il valore del fattore giromagnetico g senza ambiguità alcuna, cioè con grandissima precisione. La trappola è costituita da due elettrodi, posti l'uno sopra l'altro a una distanza b e allo stesso potenziale V = − V0, e da un elettrodo cilindrico al potenziale V = + V0. La superficie dei primi due elettrodi, a forma di tazza soddisfa l'equazione z2 = (r2 + b2)/2, dove z è la coordinata nella direzione del campo magnetico e r il raggio del cilindro. L'elettrodo laterale è un anello cilindrico la cui forma è descritta dall'equazione r2 = b2 + 2z2. La distanza b è di 0,473 cm. Il vuoto nella trappola è di 10-14 torr.
L'hamiltoniana non relativistica che descrive l'elettrone in questa situazione è
dove MB è il magnetone di Bohr, P2 è l'operatore momento cinetico,
e B il campo magnetico esterno, uniforme nella direzione dell'asse z:
B = (0, 0, Bz).
Il corrispondente potenziale vettore è
Gli autovalori dell'equazione di Schrödinger, la cui hamiltoniana sia data dalla (20), sono espressi in funzione dei numeri quantici n, nz e nm, che possono assumere solo valori interi:
Nel primo termine compare il numero quantico principale n e la frequenza di ciclotrone ωc′. L'apice sta a ricordare che la frequenza di ciclotrone è spostata rispetto al valore ωc = eB/mc a causa della presenza del campo elettrico:
(dove ωm è la frequenza di magnetone definita più sotto).
Il secondo termine rappresenta la frequenza di oscillazione nella direzione dell'asse z (che è la direzione di B), cioè la frequenza del moto assiale. Questa frequenza dipende dal campo elettrostatico
Il terzo termine rappresenta il moto del centro dell'orbita di ciclotrone. Il centro dell'orbita ruota attorno all'asse z con una frequenza (la frequenza di magnetone)
Il quarto termine è quello che rappresenta lo stato di spin del sistema. Il numero quantico ms vale ±1/2, gli autovalori dell'energia associata al numero quantico ms sono
Nel limite V0 → 0, cioè nel limite in cui il potenziale applicato alla trappola è estremamente debole, gli autovalori dell'energia del sistema si riducono agli autovalori dei livelli di Landau-Rabi,
che si suddividono in due serie di livelli, secondo il valore di ms:
L'esperimento di Dehlmet e altri (v., 1981) consiste nell'indurre transizioni da uno stato all'altro del sistema elettrone-campo magnetico e nel misurarne le frequenze di transizione.
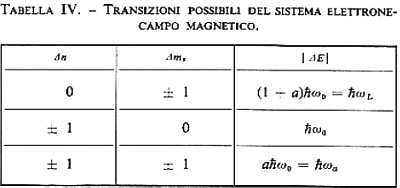
La tab. IV indica le possibili transizioni eccitate nella misura di (g − 2) e le diverse grandezze che se ne possono dedurre.
La transizione che permette di determinare ωa è quella che dà luogo a un cambiamento simultaneo del numero quantico principale n e del numero quantico di spin ms di un'unità. Questa transizione è indotta applicando un campo magnetico inomogeneo oscillante a una frequenza molto vicina alla frequenza ωα. Nell'esperimento di Dehlmet e altri (v., 1981) si inducono tutte le transizioni elencate sopra e si può misurare quindi sia ωα che ω0. La misura di ωα e di ω0 è essenziale per dedurre α.
La tab. V dà le misure delle diverse frequenze, con i relativi errori.
d) L'anomalia del muone (teoria).
A causa delle correzioni radiative anche il valore del rapporto giromagnetico del muone è diverso dal valore 2 predetto dalla teoria di Dirac.
Gli esperimenti per misurare il momento magnetico del muone hanno messo in evidenza che anche le interazioni forti contribuiscono al suo valore. Al CERN sono stati fatti tre esperimenti di precisione sempre crescente.
Le ragioni per fare questi esperimenti, ognuno dei quali è durato circa cinque anni, sono due. La prima è verificare se la teoria predice correttamente il valore dell'anomalia senza introdurre alcuna modifica alle regole del calcolo. La seconda è esplorare se il muone è soggetto, oltre che alle interazioni elettromagnetiche, ad altre interazioni di natura diversa. Il muone permette di esplorare distanze estremamente piccole (circa 10-15 cm). È grazie a questa sensibilità per le piccole distanze che si sono potuti mettere in evidenza i contributi adronici al momento magnetico del muone. L'elettrone è molto meno sensibile a questi effetti virtuali forti, poiché essi sono ridotti del rapporto (me/mμ)2, cioè sono circa diecimila volte più piccoli.
Il valore teorico e quello sperimentale del rapporto giromagnetico g sono in perfetto accordo tra loro: non differiscono l'uno dall'altro entro l'errore di 0,01 ppm. La misura del rapporto giromagnetico del muone, insieme con quelle del rapporto giromagnetico dell'elettrone, della costante di Rydberg, della velocità della luce e della frequenza del maser di idrogeno, è tra le misure più accurate in fisica.
Nella fig. 5 sono mostrati i diagrammi di Feynman dei contributi adronici (H) al (g − 2) del muone. Il calcolo di questi diagrammi è estremamente complicato e non è quindi il caso di riportarlo in questo articolo.
L'espressione del (g − 2) del muone nella teoria elettrodinamica è
Il contributo adronico al valore di αμ è
αμ(ad) = 702 (19) × 10-10, (30)
che si può anche scrivere (60,2 ± 1,6) ppm. L'errore è dovuto interamente all'incertezza con cui è misurato il rapporto
R = σ(e+e- → adroni)/σ(e+e- → μ+μ-). (31)
Il rapporto R è stato misurato negli anelli di accumulazione di elettroni-positoni e in esperienze di fotoproduzione. Si noti che il calcolo di aμ comporta l'uso della misura della sezione d'urto di annichilazione elettrone-positone in stati finali adronici. I processi naturali sono legati tra loro, in questo caso, tramite un fenomeno raro, cioè poco probabile, ma estremamente importante, come la polarizzazione dello stato di vuoto.
Un'altro contributo importante, che si dovrebbe poter misurare in un prossimo futuro, è dovuto alle interazioni elettrodeboli.
Al CERN due gruppi (v. Rubbia e altri, 1983; v. Darriulat e altri, 1983) hanno verificato sperimentalmente l'esistenza dei bosoni vettoriali W± e Z0, predetti dalla teoria di Glashow, Salam e Weinberg.
Il contributo elettrodebole al valore di aμ è
aμ(debole) = 195(1) × 10-11 (32)
oppure (1,7 ± 0,009) ppm. La fig. 6 mostra i diagrammi di Feynman del primo ordine che contribuiscono al (g − 2) del muone.
Il valore teorico del momento magnetico anomalo del muone è
aμ(teoria) = 1 165 920 2(20) × 10-10 (1,7 ppm), (33)
in ottimo accordo con l'esperimento del CERN (v. Comley e altri, 1981):
oppure, facendo la media pesata dei due risultati,
aμ = 1 165 924 0(85) × 10-10 (7,3 ppm). (36)
L'errore è prevalentemente statistico (7,0 ppm); l'errore sistematico è di 1,5 ppm. Questa misura mette in evidenza in modo chiaro l'esistenza degli effetti adronici su sistemi che sembrano, a prima vista, solo di natura elettrodinamica.
È importante osservare che qualsiasi modificazione del propagatore fotonico o qualsiasi nuova particella che si accoppiasse sia con l'elettrone sia con il muone darebbero luogo a un cambiamento del valore dell'anomalia aμ di un fattore (mμ/me)2, più grande del cambiamento indotto nel valore di ae. Tenendo presente questo fatto ed escludendo che esistano particelle che si accoppiano solo con l'elettrone, il risultato della misura di aμ assicura che ae è una ‛pura grandezza elettrodinamica' (e solo elettrodinamica) fino a tre parti in 1010.
e) L'anello di accumulazione di muoni.
Nel periodo compreso fra il 1959 e il 1977 furono fatte al laboratorio del Centro Europeo Ricerche Nucleari (CERN) di Ginevra tre misure dell'anomalia del momento magnetico del muone.
La grandezza che si misura, in questi esperimenti, è la frequenza di precessione ωa. Essa è la differenza tra la frequenza di precessione dello spin ωs e la frequenza di ciclotrone ‛ in un campo magnetico. Nel caso in cui B è perpendicolare all'orbita del muone le formule diventano semplici. Indicando con
il fattore di Lorentz, esse sono
e, infine,
Il terzo esperimento fatto al CERN si basava su un'osservazione importante circa il moto dello spin del muone in un campo magnetico ed elettrico. L'equazione di precessione è data da
dove θR è l'angolo tra la direzione dello spin del muone (s) nel sistema a riposo del muone e la direzione della velocità del muone β = v/c nel sistema del laboratorio. I campi B ed E e il tempo t sono calcolati nel sistema del laboratorio. Se si sceglie la condizione sperimentale in modo che sia
allora la frequenza di precessione ωa dipende solo dal campo magnetico B e non dipende da E. L'equazione (41) è soddisfatta se γ = 29,3, cioè se pμ = 3,09 GeV/c. Questa scelta permette di separare le funzioni del campo magnetico da quelle del campo elettrico nell'anello di accumulazione di muoni. Il campo magnetico B e uniforme e fissa la frequenza ωa; il campo elettrico di quadrupolo origina la forza verticale che costringe il muone a descrivere una traiettoria che oscilla attorno a un piano orizzontale, sul quale giacciono le orbite di equilibrio di momento compreso in un intervallo pμ ± Δpμ.
La fig. 7B mostra il magnete dell'anello di accumulazione di muoni. L'intensità del campo magnetico B = 1,47 tesla è uniforme entro una parte per milione (1 ppm).
La fig. 8 mostra il quadrupolo elettrico e la fig. 9 mostra la modulazione del conteggio degli elettroni di decadimento. La frequenza di modulazione dei dati non è altro che ωa, che si può, quindi, determinare analizzando la dipendenza temporale dei prodotti dei decadimenti dei muoni. Determinata ωa, noto B, che si misura con le tecniche della risonanza magnetica nucleare, si deduce il valore di aμ. Questa operazione non è affatto semplice e richiede la determinazione di altre grandezze. La larghezza della curva di distribuzione della frequenza ωa è data da
dove τμ è la vita media del muone.
La quantità γτμ è la vita media del muone nel sistema di riferimento del laboratorio. Il suo valore è circa 64 × 10-6 s ed è da confrontarsi con il valore della vita media del muone nel sistema a riposo: τμ = 2,2 × 10-6 s.
Per rendere più comprensibile l'esperimento del muone è necessaria qualche precisazione.
Per misurare l'anomalia del muone si utilizza il metodo di precessione. Esso consiste nel determinare la variazione, in funzione del tempo, della polarizzazione longitudinale (s • β). La variazione nel tempo della quantità (s • β) è modulata alla frequenza ωa. L'esperimento consiste nel preparare un fascio di muoni inizialmente polarizzati longitudinalmente, nell'accumularli in un campo magnetico e nel misurare la quantità (s • β) nel tempo. Quest'ultima varia nel tempo a causa dell'interazione tra il momento magnetico e il campo magnetico. Uno dei maggiori problemi nella misura del momento magnetico anomalo del muone risiede nel fatto che il muone è una particella instabile, che decade dopo circa 2 μs. La quantità (s • β), cioè la componente dello spin nella direzione della quantità di moto, oscilla nel tempo, con moto periodico di periodo Ta = 2π/ωa. La misura di un fenomeno oscillatorio è tanto più precisa quanto più si protrae nel tempo. Questo si può facilmente comprendere: infatti supponiamo che si vogliano contare n cicli di un'onda, in un tempo t, con l'errore di un ciclo. Si ha, allora
Dalla relazione precedente si deduce che l'errore nella misura della frequenza decresce al crescere del tempo di misura. È quindi estremamente vantaggioso accumulare i muoni nel campo magnetico il più a lungo possibile. Nel caso degli elettroni questo tempo è limitato solo dalla qualità della ‛trappola', o, più correttamente, dalla natura della perturbazione necessaria per accumulare le particelle cariche. Nel caso dei muoni occorre allungare la loro vita media, cioè accumulare muoni di altissima energia in un campo magnetico. Occorre anche qui introdurre una perturbazione per fare restare il più a lungo possibile i muoni nella ‛trappola', ma il parametro più importante è la vita media, cioè l'aumento della vita media del muone misurata nel laboratorio. Il tempo trascorso dal muone nel campo magnetico dà luogo a un reale guadagno, poiché ωa, come si è visto più sopra, non dipende dall'energia del muone. Grazie all'aumento relativistico della vita media del muone nel laboratorio, la modulazione di (g − 2) può essere misurata su un periodo di tempo più grande.
Il muone è creato nel decadimento π+ → μ+ + νμ e π- → μ- + nμ e, siccome le interazioni deboli violano la simmetria di parità, il muone è completamente polarizzato nella direzione della sua quantità di moto (nel sistema a riposo del pione). Una selezione opportuna delle quantità di moto dei muoni nel sistema del laboratorio permette di ottenere un fascio di muoni inizialmente polarizzato longitudinalmente, con un grado di polarizzazione del 96%.
L'analisi della polarizzazione longitudinale del fascio di muoni in funzione del tempo si ottiene tenendo conto del fatto che gli elettroni che provengono dal decadimento dei muoni hanno una distribuzione angolare asimmetrica a causa della non conservazione della parità. Si può dimostrare che il numero di elettroni di decadimento, aventi una energia opportunamente scelta, misurato da un contatore di elettroni che si trovi in una posizione azimutale fissa rispetto al punto di iniezione dei muoni, è dato dalla funzione seguente
dove N0 è il numero di muoni accumulati nell'anello di accumulazione, τ è la vita media del muone nel laboratorio, A è un parametro che dipende dalla polarizzazione del fascio e dalla modalità di rivelazione degli elettroni di decadimento, ωa è la frequenza di modulazione di (g − 2), cioè la frequenza con cui lo spin ruota rispetto alla quantità di moto, e ϕ è una fase iniziale che dipende dal metodo di iniezione dei muoni nell'anello.
f) Una digressione: la misura della vita media del muone.
La misura della vita media del muone su orbita chiusa permette di verificare la teoria della relatività speciale di Einstein: fornisce una prova sperimentale del paradosso dei gemelli, dà un limite superiore per la granularità dello spazio-tempo e consente di verificare l'invarianza CPT per le interazioni deboli.
La vita media in volo è uno dei parametri con cui si analizza la distribuzione temporale degli elettroni di decadimento. L'esperimento che misura la vita media del muone non è così semplice come può sembrare, infatti i muoni devono descrivere orbite stabili nell'anello. La diminuzione dell'intensità del fascio di muoni nell'anello di accumulazione deve essere associata soltanto al decadimento dei muoni e non all'instabilità orbitale del fascio di muoni. Questo non è facile a ottenersi, poiché i metodi per rendere stabile il fascio devono essere efficienti nei primi microsecondi.
La differenza tra il valore sperimentale e il valore teorico è di (0,9 ± 0,4) × 10-3.
Prima che si facessero esperimenti su orbita chiusa erano state fatte esperienze con fasci di pioni, di kappa e di muoni percorrenti traiettorie rettilinee.
Hafele e Keating (v., 1972) hanno verificato la dilatazione dei tempi facendo percorrere a due orologi di cesio un viaggio attorno alla Terra. Il loro esperimento verifica la dilatazione dei tempi, a velocità relativamente piccole rispetto alla velocità della luce, con una precisione del 10%. Si presti attenzione al fatto che, mentre la precisione con cui si è verificato l'effetto è solo del 10%, la sensibilità degli orologi atomici al cesio è enorme: 1 parte in 1013; l'effetto è molto piccolo, a causa delle basse velocità raggiunte dai mezzi di trasporto.
Nell'esperimento del CERN il muone percorre una traiettoria circolare e la sua vita media nel sistema di riferimento del laboratorio è confrontata con la vita media del muone a riposo nel laboratorio. Il fascio di muoni nell'anello percorre in media qualche migliaio di giri prima di disintegrarsi nei prodotti di decadimento elettrone-neutrino-antineutrino. Alcuni muoni decadono dopo cinque o sei vite medie e percorrono centinaia di chilometri prima di decadere. I muoni in moto hanno una velocità di 0,99964 c, dove c è la velocità della luce, e vivono più a lungo dei muoni a riposo nel laboratorio. Questo risultato è straordinario e l'intuizione non lo accetta facilmente, benché sia la manifestazione di una legge di natura e non mascheri alcun paradosso.
6. Verifiche dell'elettrodinamica negli esperimenti di alta energia
Le verifiche della QED alle alte energie meriterebbero un articolo di rassegna a sé stante. Qui ne illustrerò alcuni aspetti, molto brevemente.
Gli esperimenti di alta energia verificano la QFD in una situazione dove il tetravettore momento trasferito nell'interazione elettrone-positone ha un valore molto grande. Gli esperimenti sinora effettuati esplorano distanze dell'ordine di 10-15-10-16 cm. Il verdetto è chiaro: le equazioni di Maxwell con le sorgenti di campo descritte dall'equazione di Dirac sono corrette. Gli anelli di accumulazione di elettroni e positoni sono strumenti possenti per creare situazioni nuove, atte a esplorare fenomeni fisici nuovi. Si può dire che tutte le predizioni fatte dalla teoria QED sui processi fisici in cui interviene solo l'interazione elettromagnetica sono state confermate dall'esperienza.
Una delle carattenstiche principali della sperimentazione con gli anelli di accumulazione è il ruolo cinematico dell'interazione elettrone-positone. Il sistema del centro di massa è un sistema estremamente privilegiato, poiché tutto il tetravettore energia-quantità di moto può creare nuove particelle o, più genericamente, nuovi stati fisici.
Il capostipite degli anelli di accumulazione elettronepositone è ADA, una macchina relativamente modesta, costruita a Frascati nel 1960 su progetto del fisico austriaco B. Touschek, che ha trascorso molti anni a Roma.
Le verifiche dell'elettrodinamica fatte con gli anelli di accumulazione elettrone-positone sono discusse utilizzando un modello che permette di apprezzare una possibile deviazione dall'elettrodinamica. Tutte le misure di sezioni d'urto fatte con ADONE (Frascati), SPEAR (Stanford University), PETRA (Amburgo), PEP (Stanford) e in Russia verificano le leggi della QED. È un vero trionfo per questa teoria.
I processi fisici che sono stati studiati alle alte energie sono:
Nella fig. 10 sono rappresentati tre diagrammi di Feynman al primo ordine in α di alcuni processi fisici che sono stati studiati in questi anni con una precisione crescente e a energie sempre più elevate. Non sono state messe in evidenza deviazioni dalla QED, pur essendo state esplorate distanze di 10-16 cm. Un'eventuale non-località dell'interazione elettrone-positone potrebbe manifestarsi a distanze minori di l0 ~ 10-16 cm. In altri termini si può affermare che la QED è valida sino a valori della massa pari a h/cl0, corrispondente a circa 50 GeV. Nonostante questi indubbi successi, la QED non può essere considerata ancora oggi del tutto soddisfacente, poiché nello sviluppo perturbativo compaiono dei termini divergenti. Essi stanno a significare che non è stata ancora data una formulazione esatta del problema fisico, anche se la teoria rinormalizzata è sufficientemente buona per predire, con grande precisione, i fenomeni dell'elettrodinamica.
7. Polarizzazione dei fasci di elettroni e positoni negli anelli di accumulazione
Un fascio di elettroni (o positoni) che si trova soggetto all'azione di un campo magnetico si polarizza. Il meccanismo di polarizzazione è dovuto all'emissione di radiazione (luce di sincrotrone) da parte di un elettrone che cambia lo stato iniziale dello spin all'atto dell'emissione (spin-flip).
Consideriamo un fascio di elettroni (e positoni), di energia E = γmc2, accumulati in un campo magnetico uniforme, dove descrivono una traiettoria circolare di raggio r. Supponiamo, inoltre, che il fascio di elettroni (e positoni) sia in uno stato di polarizzazione nullo, cioè che il numero di elettroni con gli spins allineati nella direzione del campo magnetico sia uguale al numero di elettroni con gli spins allineati nella direzione opposta al campo magnetico. Al passare del tempo il fascio di elettroni (e positoni) acquista una polarizzazione nella direzione del campo, cioè nella direzione perpendicolare a quella del moto degli elettroni (e positoni). La polarizzazione cresce al passare del tempo sino ad acquistare un valore limite ξ0:
τ0 è la costante di tempo del processo di polarizzazione. Il valore di τ0 è
dove r = 1/∣ β ∣.
Il vettore polarizzazione è perpendicolare sia al vettore velocità sia al vettore accelerazione, cioè giace nella direzione del campo magnetico. I positoni si dispongono parallelamente al campo magnetico, gli elettroni nella direzione opposta al campo magnetico.
La probabilità di emettere, nell'unità di tempo, un fotone cambiando la direzione dello spin (spin-flip) è molto minore della probabilità di emettere un fotone senza alterare la direzione dello spin. Ciononostante, se si aspetta un tempo sufficientemente lungo, il fascio si polarizza. Questo è un effetto elettrodinamico sorprendente.
La probabilità dell'emissione di un fotone (cioè della radiazione) con spin-flip è
dove ξ indica la direzione dello stato iniziale dello spin nel sistema a riposo dell'elettrone, mentre β̂ β˄˙ e rappresentano i versori (vettori unitari) della velocità e dell'accelerazione.
Il rapporto tra la potenza irraggiata da un fascio di elettroni con spin-flip e quella senza spin-flip è
La scelta del segno ± dipende dallo stato iniziale dello spin. Quando γ tende a γc = (mcξ/ℏ)1/2 le due potenze si uguagliano. Il valore di γc è irraggiungibile con gli attuali metodi di accelerazione, infatti esso corrisponde a energie comprese tra 102 e 103 TeV.
I tempi τ0 dipendono dall'energia e sono generalmente molto lunghi. Esistono dei metodi per ridurre i valori τ0. Nel LEP (Large Electron Positron collider), in costruzione a Ginevra, gli elettroni raggiungeranno energie di 50-100 GeV. Il tempo di polarizzazione è di qualche ora, a causa del grande raggio (circa 4 km) dell'anello di accumulazione. Con metodi adeguati, cioè costruendo campi magnetici speciali (wigglers), opportunamente localizzati lungo la traiettoria, si può ottenere un fascio polarizzato in mezz'ora.
Le prime misure di polarizzazione sono state fatte a Novosibirsk nel 1970 nell'anello di accumulazione VEP-2, poi nel 1972 a Orsay in ACO e successivamente in tutti gli anelli di accumulazione.
La descrizione corretta di questo processo è possibile solo nello schema della teoria QED. La prova sperimentale della sua esistenza è una verifica ulteriore dell'elettrodinamica, poiché è un fenomeno tipicamente quantistico. La comprensione approfondita di questi esperimenti richiede un'analisi dei fenomeni di depolarizzazione di un fascio in un campo magnetico. Questa analisi non è semplice e costituisce un problema di dinamica dell'elettrone la cui soluzione è piuttosto complicata.
8. Conclusioni
L'elettrodinamica quantistica è una teoria estremamente affascinante e potente che spiega la legge secondo cui la carica elettrica interagisce col campo elettromagnetico. Verificata sperimentalmente con un grado di precisione che ha dell'incredibile, ha peraltro permesso di scoprire fatti nuovi che hanno influito sulla nostra società e sul nostro modo di vivere (basti pensare al laser). Infine costituisce il modello di riferimento per la costruzione delle moderne teorie (teorie di gauge) delle interazioni fondamentali.
Ciononostante si ha l'impressione che il processo di base non sia stato ancora completamente compreso: la tecnica della rinormalizzazione è un po' troppo complicata per spiegare un fenomeno fisico così fondamentale come l'interazione tra la carica elettrica e il campo elettromagnetico. Di fatto l'eliminazione delle divergenze ha permesso di descrivere con un elevato grado di precisione una serie di fenomeni fisici altrimenti non comprensibili, ma le divergenze non possono essere un fenomeno reale. Comunque la possibilità di raggiungere energie sempre più elevate e precisioni sempre più spinte aiuterà a comprendere sempre meglio l'interazione tra la carica elettrica e il campo elettromagnetico. È evidente che la nuova formulazione conterrà tutti i fenomeni fisici brevemente descritti in questa rassegna.
BIBLIOGRAFIA
Bethe, H.A., The electromagnetic shift of energy levels, in ‟Physical review", 1947, LXXII, pp. 339-341.
Bethe, H. A., Salpeter, E. E., Quantum mechanics of one- and two-electron atoms, Berlin 1957.
Breit, G., Does the electron have an intrinsic magnetic moment?, in ‟Physical review", 1947, LXXII, p. 984.
Combley, F., Farley, F. J. M., Picasso, E., The CERN muon (g - 2) experiments, in ‟Physics letters. Section C. Physics reports", 1981, LXVIII, 2, pp. 93-119.
Combley, F., Picasso, E., Some topics in quantum electrodynamics, in Proceedings of the International School of Physics ‛Enrico Fermi', 1980, LXVIII, pp. 717-764.
Darriulat, P., Di Lella, L. e altri (Collaborazione UA2), Evidence for Z0 - e+ e- at the CERN pp- collider, in ‟Physics letters", 1983, CXXIX, pp. 130-140.
Dehlmet, H. G. e altri, New comparison of the positron and the electron g factors, in ‟Physical review letters", 1981, XLVII, pp. 1679-1682.
Dirac, P. A. M., The quantum theory of the emission and absorption of radiation, in ‟Proceedings of the Royal Society of London", Series A, 1927, CXIV, pp. 243-265.
Dyson, F. J., The radiation theories of Tomonaga, Schwinger and Feynman, in ‟Physical review", 1949, LXXV, pp. 486-502.
Fermi, E., Sopra l'elettrodinamica quantistica, in ‟Atti della Reale Accademia Nazionale dei Lincei", 1930, XII, pp. 431-435.
Fermi, E., Nuovi sviluppi dell'elettrodinamica quantistica, in Collezione dei lavori di Fermi. Accademia dei Lincei, vol. II, Conferenze di fisica atomica, Roma 1965, pp. 744-755.
Feynman, R. P., The theory of positrons, in ‟Physical review", 1949, LXXVI, pp. 749-759.
Hafele, J. C., Keating, R. E., Around-the-world atomic clocks: predicted relativistic time gains, in ‟Science", 1972, CLXXVII, pp. 166-167.
Heisenberg, W., Über die mit der Entstehung von Materie us Strahlung verknüpften Ladungsschwankungen, Dresden 1934, pp. 317-322.
Heisenberg, W., Pauli, W., Zur Quantendynamik der Wellenfelder, in ‟Zeitschrift für Physik", 1929, LVI, pp. 1-61.
Hughes, V. W. e altri, The Lamb shift, in ‟Muonium atomic physics", 9 July 1984.
Hughes, V. W., Kinoshita, T., Electromagnetic properties and interactions of muons, in Muon physics (a cura di V. W. Hughes e C. S. Wu), vol. I, New York 1977, pp. 12-187.
Klitzing, K. von, Dorda, G., Pepper, M., New measurement for high-accuracy determination of the fine-structure constant based on quantized Hall resistance, in ‟Physical review letters", 1980, XLV, pp. 494-497.
Kusch, P., Foley, H. M., Precision measurement of the ratio of the atomic ‛g values' in the 2P3/2 and 2P1/2 states of Gallium, in ‟Physical review", 1947, LXXII, pp. 1256-1257.
Lamb, W. E., Retherford, R. C., Fine structure of the hydrogen atom by a microwave method, in ‟Physical review", 1947, LXXII, pp. 241-243.
Lee, T. D., Particle physics and introduction to field theory, New York 1981.
McConnel, J., Quantum particle dynamics, Amsterdam 1958.
Nafe, J. E., Nelson, E. B., Rabi, I. D., The hyperfine structure of atomic hydrogen and deuterium, in ‟Physical review", 1947, LXXI, pp. 914-915.
Olsen, P. T., Williams, E. R., New measurement of the proton gyromagnetic ratio and a derived value of the fine-structure constant accurate to a part in 107, in ‟Physical review letters", 1979, XLII, pp. 1575-1579.
Rubbia, C. e altri (Collaborazione UA1), Experimental observation of lepton pairs of invariant mass around 95 GeV/c2 at the CERN SPS collider, in ‟Physical letters", 1983, CXXXVI B, pp. 398-410.
Schwinger, J., On quantum electrodynamics and the magnetic moment of the electron, in ‟Physical review", 1948, LXXIII, p. 416.
Schwinger, J., On gauge invariance and vacuum polarization, in ‟Physical review", 1951, LXXXII, pp. 664-679.
Tomonaga, S., On infinite field reactions in quantum field theory, in ‟Physical review", 1948, LXXIV, p. 224.
Tsui, D. C., Gossard, A. C., Fied, B. F., Cage, M. E., Dzinba, R. F., Determination of the fine structure constant using GaAs-Alx Ga1-xAs heterostructures, in ‟Physical review letters", 1982, XLVIII, pp. 3-6.