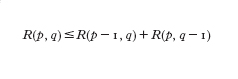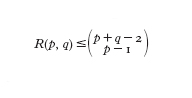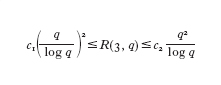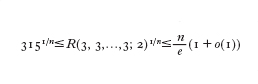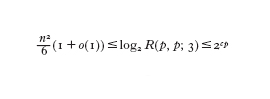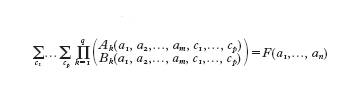Finito

Finito

(XV, p. 399)

Matematica del finito

Diversi filoni della ricerca matematica che mostrano particolare vitalità si possono ricondurre all'interesse per i problemi del finito. L'analisi combinatoria studia i raggruppamenti di elementi in insiemi in generale discreti, più spesso finiti; si tratta di una branca classica (v. combinatoria, analisi, X, p.912; App. IV, i, p.490; V, i, p. 684) che si è sviluppata impetuosamente nella seconda metà del Novecento, anche in ragione della sua rilevanza per settori applicativi legati alle nuove tecnologie, per es. nell'informatica.

Le esigenze della programmazione degli elaboratori elettronici e della messa a punto di metodi computazionali per arrivare alla soluzione effettiva dei problemi formulati in linguaggio matematico contribuisce a portare in primo piano la dimensione finita (v. computazionali, metodi, in questa Appendice). Esistono inoltre ricerche logico-matematiche che risalgono a discussioni sui fondamenti della matematica nell'Ottocento, le quali ripropongono problemi in parte tralasciati dalla matematica dell'infinito e del continuo, come quelli della decidibilità e della costruibilità degli enti matematici in un numero finito di passi (v. continuità, XI, p. 237; infinito, XIX, p. 205; numero: Inumeri e l'infinito, XXV, p.31; logica e informatica, App.V, iii, p.238).

Per illustrare aspetti, problemi e metodi della matematica del f. verranno discusse in questa voce alcune fra le questioni più significative, e precisamente: la riduzione di problemi di carattere infinito ad altri di carattere finito; le geometrie finite e i quadrati latini; le regolarità 'inevitabili' e i numeri di Ramsey; il problema dei quattro colori; carte e permutazioni; e la classificazione dei gruppi finiti.  *

aspetti, problemi e metodi

di Antonio Machì

La riduzione dall'infinito al finito

Un esempio di questa tecnica di riduzione è il classico modello di Kronecker, che permette di stabilire se un polinomio a coefficienti interi sia o meno riducibile (sempre sugli interi) e, nel caso lo sia, di fornire una fattorizzazione in fattori irriducibili.Il metodo consiste nell'operare una riduzione al caso finito trasformando il problema in quello della fattorizzazione di un intero.Tuttavia, data la complessità di quest'ultimo problema, questa tecnica è del tutto impraticabile già per polinomi di quinto grado. L'interesse per tale metodo sta piuttosto nel fatto che permette di dimostrare che il problema della fattorizzazione è decidibile: è possibile cioè in un numero finito di passi (per quanto grande) stabilire se un polinomio a coefficienti interi sia riducibile o meno.

Un modo diverso di affrontare il problema è quello di prendere i coefficienti del polinomio modulo un numero primo p. Poiché su un campo finito esiste solo un numero finito di polinomi di un dato grado, è possibile stabilire in un numero finito di passi se un polinomio è riducibile dividendolo per tutti quelli di grado inferiore; tuttavia anche in questo caso il numero di operazioni da fare può diventare intrattabile. È vero che se un polinomio è irriducibile modulo p esso lo è anche sugli interi; nulla però si può concludere sulla sua riducibilità sugli interi se esso si riduce modulo p: vi sono polinomi che sono riducibili modulo ogni primo ma che sono irriducibili sugli interi (un esempio è il polinomio x⁴11).

A partire dagli inizi degli anni Sessanta sono stati individuati metodi più efficaci, come il metodo di E.R. Berlekamp, il quale, fissato un primo p, permette di trovare una fattorizzazione di un polinomio modulo p, e, se p supera un certo intero, di trovarne poi una sugli interi, o dimostrare che il polinomio è irriducibile. Questo metodo si presta facilmente a essere implementato su computer. Esso sfrutta il teorema cinese del resto e le proprietà dei campi finiti per trovare una fattorizzazione parziale; ripetendo il procedimento e stabilendo a priori il numero di fattori irriducibili del polinomio (con metodi lineari, in funzione del rango di una certa matrice) si giunge alla fattorizzazione completa.Per ottenere la fattorizzazione sugli interi si sfrutta il fatto che è possibile stabilire una maggiorazione N per il modulo dei coefficienti di ogni possibile fattore del polinomio dato; osservando poi che una congruenza tra due polinomi, modulo N, è in realtà un'uguaglianza, si può stabilire se una fattorizzazione modulo p.2N provenga o meno da una fattorizzazione sugli interi.

Il metodo è piuttosto efficace: per p abbastanza piccolo, vi sono algoritmi che richiedono un numero di operazioni dell'ordine di n³1pn² log n, dove n è il grado del polinomio; se p è grande, gli algoritmi più efficaci hanno una complessità (v. informatica, App. V) dell'ordine di n²(log p)³ log r, dove r è il numero dei fattori: la dipendenza da p è quindi piuttosto forte.

Conviene allora prendere un primo più piccolo, fattorizzare modulo questo primo e poi, usando una tecnica dovuta a K. Hensel (analoga a quella che permette di determinare lo sviluppo p-adico di un numero algebrico), sollevare la fattorizzazione a una fattorizzazione sugli interi modulo p^k, dove k è tale che p^k.2N. Occorre inoltre vedere se i prodotti dei fattori, nelle varie combinazioni, dividono il polinomio dato.

Quest'ultima tappa può però essere di complessità esponenziale nel numero r dei fattori: nel caso peggiore occorre infatti effettuare un numero di divisioni dell'ordine di 2^r21. A.K. Lenstra, H.W. Lenstra e L. Lovász hanno risolto questo problema nel 1982, ma il loro metodo (detto delle basi ridotte) sembra avere un carattere più teorico che pratico.

Geometrie finite e quadrati latini

Il problema di sapere per quali n esista un numero massimo di quadrati latini n3n a due a due ortogonali (v. combinatoria, analisi, App. IV) resta aperto.Si dimostra facilmente che per ogni n.1 questo massimo è n21.Se n è primo, allora questo massimo è raggiunto: la dimostrazione si ottiene identificando i simboli della tabella del quadrato latino con gli elementi del campo di ordine primo p e utilizzando la somma e il prodotto di questo campo.In modo analogo si vede che lo stesso accade per n potenza di un primo.Questo problema è legato a quello dell'esistenza di piani proiettivi di ordine n (v.combinatoria, analisi, App. IV).

La congettura che un piano proiettivo di ordine n esista solo nel caso di n potenza di un primo rimane a tutt'oggi un problema aperto.Si è anche cercato un controesempio con n510, dato che 10 è il primo intero (diverso da 6) che non sia potenza di un primo.La ricerca di un piano di ordine 10 è durata a lungo, finché nel 1989 C.W.C. Lam, L.Thiel e S.Swiercz hanno annunciato che una ricerca esaustiva di tutti i casi possibili (la quale ha impiegato 3000 ore di lavoro del computer) li aveva portati a concludere che, con probabilità altissima, un tale piano non esiste. Il metodo, che si basa su idee della teoria dei codici correttori, consiste nel determinare configurazioni di 19 punti che non si possono estendere a un piano di ordine 10. In un articolo pubblicato sulla rivista Canadian journal of mathematics gli autori presentano tali risultati come sperimentali, non escludendo la possibilità che errori nella programmazione o di hardware possano inficiare la loro conclusione, ma spiegando anche perché ritengono che la probabilità che esista un piano di ordine 10 non individuato dalla ricerca con il computer sia 'infinitesima'.

Un piano proiettivo di ordine n contiene n²1n11 punti, e, per dualità, n²1n11 rette.Il più piccolo piano proiettivo (a meno di isomorfismi) è il piano di Fano, di ordine 2, e dunque con 7 punti e 7 rette, e nel quale ogni retta contiene 3 punti e ogni punto appartiene a 3 rette.Si può rappresentare con la configurazione ottenuta tracciando il cerchio inscritto a un triangolo e le tre mediane: i 7 punti così ottenuti (incluso il centro del cerchio) sono i 'punti' del piano di Fano, gli insiemi di 3 punti su ciascun lato del triangolo e sul cerchio costituiscono le 7 rette. Le collineazioni di questo piano, cioè le permutazioni dei 7 punti che portano rette in rette, sono in numero di 168 e formano un gruppo semplice, il celebre gruppo scoperto da F.Klein nel 1878 nello studio delle permutazioni delle radici di una certa equazione polinomiale.Lo studio di strutture finite e dei loro gruppi di automorfismi ha costituito un ricco filone di ricerca per la scoperta di gruppi semplici (v. oltre: La classificazione dei gruppi finiti).

È tuttora aperto il problema di trovare una dimostrazione geometrica del teorema secondo il quale un corpo finito è commutativo e quindi è un campo (teorema di Wedderburn). In un piano finito possono valere o meno il teorema di Desargues e quello di Pappo, che si enunciano in modo analogo al caso classico del piano euclideo. Analogamente al caso delle coordinate cartesiane, prendendo come punti le terne di elementi di un corpo (a meno di un fattore di proporzionalità) e come rette gli insiemi di terne che soddisfano un'equazione lineare, si ottiene un modello di piano proiettivo, un piano coordinato sopra un corpo. Non tutti i piani finiti si ottengono in questo modo: nei piani coordinati sopra un corpo vale infatti il teorema di Desargues. Il teorema di Pappo vale se e solo se il corpo è commutativo e poiché, per il teorema di Wedderburn, un corpo finito è commutativo, nei piani affini finiti il teorema di Pappo è conseguenza del teorema di Desargues.Se si riuscisse a dare una dimostrazione geometrica di quest'ultimo fatto si avrebbe una dimostrazione geometrica del teorema di Wedderburn.

Regolarità inevitabili e numeri di Ramsey

fig. 1

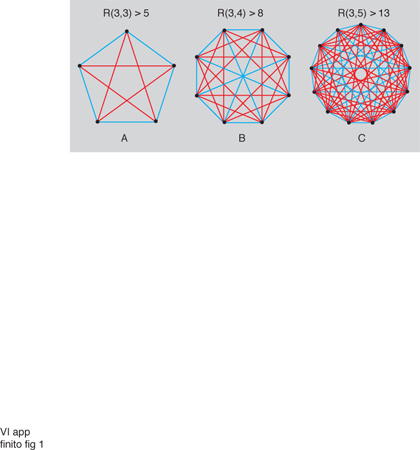
Il principio dei cassetti (pigeonhole principle) afferma che se k11 oggetti sono distribuiti in k cassetti, uno dei cassetti contiene almeno due oggetti. Una delle conseguenze di questo semplice fatto (e della sua profonda generalizzazione nota come teorema di Ramsey) è che una struttura, per quanto irregolare essa sia, contiene sempre una sottostruttura di una data cardinalità che presenta un certo grado di regolarità: questo significa che 'un completo disordine è impossibile'. Nella teoria dei grafi (v. grafo, App. IV) questo fenomeno ha luogo per es. quando si colorano gli archi del grafo completo K_n con due colori, la scelta del colore di ogni arco essendo arbitraria (il grafo completo K_n è il grafo con n vertici in cui ogni coppia di vertici è unita da un arco). Se n è abbastanza grande si troverà sempre un sottografo completo K_m, dove m è fissato in anticipo, nel quale tutti gli archi hanno lo stesso colore. Se G è un grafo qualunque, questo risultato si enuncia dicendo che, per n abbastanza grande, o G oppure Ḡ (il complementare di G) contiene un grafo K_m (Ḡ ha gli stessi vertici di G e due suoi vertici sono adiacenti se e solo se non lo sono in G). Più in generale la 'regolarità' può avere la forma "o G contiene un K_p oppure Ḡ contiene un K_q": fissati p e q, il più piccolo numero n di vertici che G deve avere perché ciò accada è un numero di Ramsey (fig. 1) e si denota con R(p, q). È chiaro che R(p, q)5R(q, p). Si può dimostrare che R(3, 3)56, R(3, 4)59, R(3, 5)514. Pochi altri valori oltre a questi sono noti e sono quelli della seguente tabella:

Come si vede, per alcune coppie p, q si conoscono soltanto il minimo e il massimo valore che può assumere R(p, q). Secondo un sentimento diffuso, è improbabile che si riescano a determinare altri valori.I numeri R(p, q) soddisfano la relazione ricorsiva:

dimostrata da P. Erdâs e G. Szekeres nel 1935.Iterando questa disuguaglianza si può stimare R(p, q) tramite i numeri R(p,1)5R(1, q)51, R(p, 2)5p, R(2, q)5q. Da queste relazioni si trae la maggiorazione:

Si conoscono anche maggiorazioni e minorazioni di carattere asintotico ma solo per alcuni valori di p; per es., per p53 e q che tende all'infinito si ha che (con c₁ e c₂ costanti)

(risultato contenuto nei lavori di Erdâs del 1959 e di M. Ajtai, J. Komlós edE. Szemerédi del 1980). Si sa inoltre che √2#R(p, p)¹/^p#4, ma non si sa nemmeno se, per p che tende all'infinito, esista il limite di R(p, p)¹/^p.

Il legame tra il principio dei cassetti e i numeri di Ramsey si vede facilmente enunciando il principio come segue: dato k, qual è il minimo numero n di oggetti tale che, distribuendo questi oggetti in k cassetti, uno dei cassetti contenga almeno due oggetti? Il problema si può generalizzare in vari modi. Per es.: dati k interi p₁, p₂,…,p_k, qual è il più piccolo numero di oggetti tale che, distribuendo questi oggetti in k cassetti, vi sia o un cassetto con p₁ oggetti, o uno con p₂ oggetti,…, o uno con p_k oggetti?Si tratta in questo caso del numero di Ramsey R(p₁, p₂,…, p_k; 1)5∑^k_i5₁(p_i21)11; il caso del principio dei cassetti è quello in cui tutti i p_i sono uguali a 2. Invece di considerare semplicemente degli oggetti, consideriamo ora coppie di oggetti: dati k interi p₁, p₂,…,p_k, qual è il minimo n tale che, ripartendo le coppie di elementi di un insieme S (con n elementi) in k famiglie A₁, A₂,…, A_k, esista per almeno un i un sottoinsieme di S con p_i elementi, tutte le coppie di elementi del quale appartengono ad A_i? È questo il caso dei grafi: gli elementi di S sono i vertici del grafo, le coppie di elementi di S sono gli archi; questi ultimi sono colorati con k colori e dunque ripartiti secondo il colore in k sottoinsiemi (gli A_i di cui sopra).È chiaro infine che si può ancora generalizzare il problema considerando, invece di coppie, sottoinsiemi con r elementi, dove r è un intero qualunque.Il teorema di Ramsey afferma che tale problema è ben posto, nel senso che il numero cercato esiste sempre; si denota con R(p₁, p₂,…, p_k; r) (v.combinatoria, analisi, App. IV).

Alcuni risultati del tipo di quelli visti sopra riguardano per es. il limite di R(3, 3,…,3; 2)¹^/n, dove n è il numero dei 3 che compaiono. Questo limite esiste, ma non si sa se sia finito o infinito. Si ha:

dove la maggiorazione, dovuta a I.Schur, risale al 1916 e non è stata ancora migliorata.Il più importante problema aperto è quello di stabilire il comportamento di R(p, p; 3); è nota la limitazione

anche se rimane qualche dubbio sulla maggiorazione (Rödl 1990).

Per illustrare la portata del teorema di Ramsey elenchiamo una serie di teoremi che possono essere visti come conseguenze del teorema stesso. 1) In una successione di n²11 interi a₁, a₂,…, a_n₂₊₁, esiste o una sottosuccessione crescente o una decrescente di lunghezza n11 (Erdös e Szekeres). Ponendo R(n11, n11; 2) al posto di n²11, il risultato segue dal teorema di Ramsey tramite la seguente procedura: coloriamo le coppie i, j, con i,j, con due colori, uno dei colori se a_i,a_j, l'altro nell'altro caso. 2) Il seguente teorema di Dilworth è un altro esempio: un insieme parzialmente ordinato con almeno ab11 elementi contiene o una catena (sottoinsieme totalmente ordinato) di a11 elementi o un'anticatena (due elementi non sono mai confrontabili) di b11 elementi.Ponendo R(a11, b11) al posto di ab11 e colorando le coppie di elementi con due colori (a seconda che i due elementi siano confrontabili o meno), un insieme di a11 elementi di un colore darà la catena, uno di b11 elementi dell'altro colore l'anticatena. 3) Colorando gli interi con un numero finito di colori, esistono tre interi x, y, z che hanno lo stesso colore e tali che x1y5z (I. Schur).Espresso nei nostri termini: per ogni r esiste n₀ tale che per n#n₀, colorando l'insieme {1, 2,…,n} con r colori esistono x, y, z in {1, 2,…,n} aventi lo stesso colore e tali che x1y5z.

Il problema dei quattro colori

fig. 2A

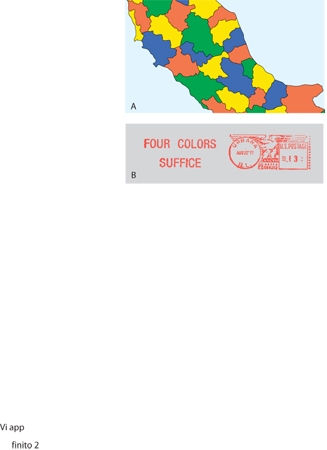
Come per la trisezione dell'angolo, il teorema di Fermat e altri problemi classici, il problema dei quattro colori si enuncia con estrema semplicità: è possibile colorare una qualunque carta geografica usando solo quattro colori e in modo tale che due regioni adiacenti non abbiano mai lo stesso colore (fig. 2A)? A causa di questa semplicità tale problema è stato oggetto di 'soluzioni' da parte di un gran numero di matematici dilettanti nel corso degli ultimi cento anni e più (analogamente ai problemi della trisezione e di Fermat). Anche alcuni matematici di professione sono caduti nella trappola dei quattro colori, tuttavia, assieme a errori, le 'dimostrazioni' contenevano a volte idee che, riprese e approfondite, hanno portato più tardi alla soluzione, positiva, del problema. Come è accaduto per es.in teoria dei numeri e in algebra con il teorema di Fermat (v. numeri, teoria dei, in questa Appendice), la ricerca di una soluzione al problema dei quattro colori ha dato origine a un gran numero di nozioni e metodi e a un'intera disciplina come la teoria dei grafi, la quale ha acquisito una vita propria sviluppandosi indipendentemente (v. combinatoria, analisi, App. V; grafo, App.IV). Il problema ammette inoltre varie formulazioni equivalenti (relative a diversi campi di ricerca) che fanno intervenire problemi di colorazione di vertici e archi di un grafo, l'esistenza di particolari cicli, la soluzione di equazioni diofantee, la ricerca delle radici di polinomi, problemi di matrici su un campo finito e così via. Questo fenomeno è comune in analisi combinatoria.

Il problema, sollevato quasi casualmente da F.Guthrie nel 1852, fu presentato ufficialmente alla comunità matematica solo nel 1878, con un articolo di A. Cayley nei Proceedings of the London Mathematical Society. L'anno dopo comparve la prima 'soluzione' a opera di un avvocato inglese, A.B.Kempe. Furono necessari undici anni prima che P.J. Heawood trovasse un errore nella dimostrazione, salvando però dell'argomento di Kempe quanto basta per dimostrare che cinque colori sono sempre sufficienti.Non solo, ma la dimostrazione di K. Appel e W. Haken, di un secolo dopo, si può vedere come una correzione molto profonda della svista di Kempe(fig. 2B). Nel frattempo, nel 1880 W. Tait aveva fornito un'altra 'dimostrazione': l'errore consisteva, in questo caso, nel supporre che un grafo planare 3-connesso (occorre rimuovere tre vertici e gli archi a essi incidenti per spezzare il grafo in due parti) ammetta un circuito hamiltoniano (un circuito che passa per ogni vertice una e una sola volta). È facile vedere come l'esistenza di un tale circuito implichi che la carta si possa colorare con quattro colori: basta colorare alternativamente con due dei colori le regioni lasciate da un lato del circuito e alternativamente con gli altri due le regioni lasciate dall'altro. Nel 1913 O.Veblen offrì la seguente formulazione equivalente: se B è la matrice di incidenza archi-regioni (tale matrice ha 1 nel posto (i, j) se l'arco i appartiene alla frontiera della regione j, e 0 altrimenti), allora esiste un vettore v a n componenti (n è il numero delle regioni) nel corpo con quattro elementi (che corrispondono ai quattro colori) tale che il vettore immagine di v secondo B ha tutte le componenti non nulle.La tecnica di Kempe consisteva nella determinazione di 'configurazioni inevitabili' e 'riducibili'; per tale scopo si sfruttava, in particolare, la relazione di Eulero V2A1F52, dove V è il numero dei vertici, A quello degli archi, F quello delle regioni o facce (v. poliedro, XXVII). Da questa relazione si deduce facilmente che esiste una regione limitata al più da cinque archi o, dualmente, un vertice di grado al più 5.I poligoni con 2, 3, 4 o 5 lati formano allora un insieme inevitabile di configurazioni, nel senso che una carta ha necessariamente una regione con 2, 3, 4 o 5 lati. Ma secondo Kempe queste configurazioni sono anche riducibili, nel senso che è possibile sopprimerne una ottenendo una carta con una regione in meno e tale che, se quest'ultima si può colorare con un certo numero di colori, lo stesso si può fare per la carta di partenza. In realtà, ciò è vero, per es., per sei colori: basta restringere a un punto la regione prescelta, colorare la nuova carta con sei colori e riproporre la faccia eliminata attribuendole uno dei colori non usati per le regioni confinanti, le quali sono al più cinque; ripetendo il procedimento si arriva a una carta con sei regioni, che ovviamente si può colorare con sei colori.Analogo, anche se un po' più delicato, è il caso dei cinque colori.

Per il caso dei quattro colori questa tecnica funziona per le regioni con 2, 3 e 4 lati, ma per quelle pentagonali la dimostrazione di Kempe è incompleta, come fece notare Heawood. La tecnica della riducibilità e le sue variazioni furono applicate in seguito da vari autori, per ottenere risultati che essenzialmente affermano che se una carta non si riesce a colorare con quattro colori, allora la carta deve avere 'molte' regioni.Nel 1922 P.Franklin dimostrò che essa ne deve avere almeno 26, numero elevato più tardi da vari ricercatori a 32, 40, e infine a 96 (risultato di W.A. Mayer del 1975). Si arriva così in modo naturale alla nozione di controesempio minimo al teorema (una forma del principio di induzione): se il teorema è falso, esiste una carta con un numero minimo di regioni per la quale il teorema è falso, vale a dire una carta che non è 4-colorabile e tale che ogni carta con meno regioni sia 4-colorabile; questa carta è un controesempio minimo al teorema (ovviamente un controesempio minimo non è unico). Se il teorema è vero, non esistono controesempi, in particolare controesempi minimi e, poiché sappiamo che ogni carta è 5-colorabile, il teorema è equivalente al fatto che non esiste una carta che richiede cinque colori e tale che ogni carta con meno regioni ne richieda quattro. Com'è d'uso in questi casi, si cerca di dimostrare la non esistenza di questa carta facendo vedere che essa dovrebbe avere troppe proprietà perché la sua esistenza non porti a contraddizioni.

Il problema si può trasformare in un problema di teoria dei grafi considerando il grafo duale della carta, e cioè il grafo i cui vertici sono punti all'interno di ogni regione (uno per ogni regione); si traccia un arco tra due di questi vertici se le due regioni sono adiacenti. Il teorema dei quattro colori diventa allora un problema di colorazione dei vertici di un grafo: si richiede una 4-colorazione che assegni colori diversi a due vertici congiunti da un arco. È facile vedere che basta ridursi al caso di grafi 3-connessi triangolari, e di qui al caso 4-connesso. Ciò fornisce un altro legame tra il teorema e i circuiti hamiltoniani, in quanto i grafi planari 4-connessi ammettono sempre un circuito hamiltoniano, per cui dimostrando che tali grafi sono 4-colorabili si avrebbe il risultato cercato. Sappiamo che c'è almeno un vertice di grado minore di 6: esprimiamo questo fatto dicendo che i vertici di grado minore di 6 formano un insieme di configurazioni inevitabili. I vertici di grado minore di 5 sono inoltre riducibili: la 4-colorabilità si riduce a quella del grafo ottenuto sopprimendo uno di questi vertici, per cui una prima proprietà di un grafo che sia un minimo controesempio è che esso non può avere vertici di grado minore di 5. Ma i vertici di grado 5 non sono in generale riducibili: come abbiamo visto, è questa l'osservazione di Heawood al lavoro di Kempe. Altri esempi di configurazioni riducibili sono: un vertice di grado 5 collegato a tre vertici consecutivi anch'essi di grado 5; un vertice di grado 5 collegato a vertici tutti di grado 6; un vertice di grado 6 collegato a tre vertici consecutivi di grado 5; un ciclo di grado superiore a 3 (abbiamo visto che possiamo supporre il grafo triangolare); un circuito di lunghezza minore di 5 rimuovendo vertici e archi del quale il grafo risultante non è più complesso e così via. La ricerca che ha portato alla soluzione si è rivolta verso la determinazione di configurazioni inevitabili e riducibili contenute in un controesempio minimo: l'insieme di Appel e Haken consta di 1936 configurazioni di questo tipo. Esse sono costruite secondo un algoritmo elaborato da H.Heesch nel 1969 e ripreso da Haken nel 1973, detto algoritmo di scarica (discharging algorithm), che consiste nell'assegnare un intero a ogni vertice, come se si assegnasse una carica elettrica, e ridistribuire le cariche secondo certe regole ('regole di scarica').Assegnando a ogni vertice v una carica di 62d(v), dove d(v) è il grado di v, dalla formula di Eulero (tenuto conto del fatto che in un grafo cubico 2A53V) si ha che la somma totale delle cariche assegnate è 12. L'importante non è tanto questo numero quanto il fatto che sia positivo; poiché si hanno cariche positive solo nei vertici di grado minore di 6, si ha una dimostrazione che questi vertici devono necessariamente esistere, sono cioè inevitabili.L'algoritmo di scarica consiste nel distribuire delle cariche dai singoli vertici ai loro vicini, in modo tale che nella nuova assegnazione ogni vertice abbia carica negativa o nulla.Ma poiché la carica totale deve restare invariata, ed è positiva, l'algoritmo deve a un certo punto incontrare delle configurazioni che impediscono la distribuzione voluta: l'insieme di queste configurazioni è cioè inevitabile.Si cerca poi di dimostrare che queste sono riducibili; se non ci si riesce, si modifica l'algoritmo di scarica fino a trovare configurazioni inevitabili e riducibili.

Lo sbocco naturale della tecnica inaugurata da Kempe è questa ricerca 'caso per caso' che viene eseguita con l'aiuto di un computer e richiede circa dieci miliardi di opzioni logiche.Si è ottenuta in questo modo una dimostrazione completamente formalizzata, al prezzo però dell'evidenza e della possibilità di coglierne il senso. Ed è per la difficoltà di accettare un risultato separato dall'enunciato da un numero di operazioni che supera di molto i limiti manuali che lo scetticismo di molti spinge ancora oggi a vedere nel lavoro di Appel e Haken più un preludio a una dimostrazione concettuale, collocata cioè nel solco della tradizione matematica, che una prova convincente e irrefutabile. Questo problema è già stato sollevato per l'esistenza del piano di ordine 10, sempre relativamente all'affidabilità dell'uso del calcolatore.Ma esso sorge anche quando si considera un risultato che, a causa della serie lunghissima di altri teoremi da cui dipende, risulta praticamente impossibile dominare: un esempio è dato dal teorema di classificazione dei gruppi semplici (v. oltre: La classificazione dei gruppi finiti).

Fra le varie formulazioni equivalenti del problema dei quattro colori vogliamo segnalarne una che è in relazione con il decimo problema di Hilbert. Questo problema si riferiva all'esistenza di un algoritmo che permetta di stabilire se un'equazione diofantea, cioè un'equazione polinomiale a coefficienti interi, ammetta o no soluzioni intere.Che un tale algoritmo in generale non esista è stato dimostrato da J.V.Matijaèeviã nel 1970. Ora, è possibile formulare molti problemi, anche lontani dalla teoria dei numeri, nella forma ';nP(n)', ovvero "ogni intero n ha la proprietà P", dove P è una proprietà decidibile: esiste cioè un algoritmo che permette di stabilire, per ogni n, se n ha la proprietà P. Da questo algoritmo è possibile poi ottenere un polinomio a coefficienti interi la cui non risolubilità in interi è equivalente al fatto che ogni n ha la proprietà P. Anche il problema dei quattro colori si può esprimere nella forma ';nP(n)' e precisamente prendendo per P la proprietà: "ogni carta con meno di n regioni è colorabile con quattro colori", la quale è ovviamente decidibile. Il polinomio che si ottiene ha però un grandissimo numero di variabili, che si possono ridurre al prezzo però di far salire il grado in modo astronomico. Se si cerca un equivalente aritmetico del problema dei quattro colori occorre allora rivolgersi ad altri problemi dell'aritmetica. Matijaèeviã ha recentemente suggerito di considerare la somma di prodotti di coefficienti binomiali, cioè formule del tipo:

dove le A e B sono forme lineari.Formule di questo tipo si possono ora verificare facilmente utilizzando i comuni sistemi di calcolo simbolico (Reduce, Maple, Mathematica ecc.).Tra queste formule ve ne sono alcune da cui segue facilmente che ogni carta è 4-colorabile. Si tratta quindi di dimostrare che almeno una di queste è vera. Osserva Matijaèeviã che la dimostrazione di Appel e Haken è una "dimostrazione fatta da un computer per computer", non è controllabile cioè da un essere umano. Anche se una "dimostrazione fatta da esseri umani per esseri umani" sarebbe la più desiderabile, una "dimostrazione fatta da computer per esseri umani", cioè una dimostrazione trovata utilizzando un computer ma verificabile da un essere umano, sarebbe di grande interesse. La formulazione data sopra in termini di somme di prodotti di simboli binomiali permetterebbe una dimostrazione di quest'ultimo tipo.

Carte e permutazioni

Il problema dei quattro colori riguarda grafi planari, grafi cioè che ammettono una rappresentazione nel piano nella quale i vertici del grafo sono rappresentati da punti e gli archi da archi di Jordan che si incontrano solo in un vertice. Una carta planare, come quella considerata nel problema dei quattro colori, è una tale rappresentazione.Il fatto che l'intersezione di due archi avvenga solo nei vertici implica che le facce sono omeomorfe a dischi piani, sono cioè 2-celle. Il complementare del grafo è quindi un'unione di 2-celle. Va osservato che uno stesso grafo può ammettere varie rappresentazioni piane non equivalenti (non omeomorfe). Disegnare un grafo nel piano è equivalente a disegnarlo sulla sfera: la corrispondenza piano-sfera si ottiene mediante la proiezione stereografica. Dalla sfera, aggiungendo dei 'manici', si ottengono le altre superfici compatte orientabili: un manico dà luogo a un toro (ciambella), due manici a un toro con due buchi e così via. Il numero dei manici è il genere della superficie. Non tutti i grafi si possono disegnare sul piano: il grafo completo con 5 vertici K₅ e il grafo bipartito completo K₃,₃ con 6 vertici sono esempi di grafi non planari, e anzi di grafi inevitabili nel senso che un grafo non planare contiene necessariamente un sottografo che si può ridurre a K₅ o a K₃,₃ contraendo alcuni archi a un punto (teorema di Kuratowski). Come per la sfera nel caso planare, esiste sempre una superficie orientabile sulla quale un grafo non planare si può disegnare in modo che le facce siano 2-celle; il genere minimo di questa superficie è il genere del grafo. Analogamente al piano, si ha una formula di Eulero per un grafo immerso in una superficie orientabile: V2A1F5222g, dove g è il genere della superficie; per la sfera si ha g50 e si ritrova la formula di Eulero precedente.Il numero χ5222g è la caratteristica di Eulero della superficie.Per colorare una carta qualunque su una superficie di genere g.0 il minimo numero di colori è dato dalla parte intera di (71√}}11}4}8g)/2 (la radice positiva del polinomio x²27x212g112). Così per il toro (g51) questo numero è 7, ed è facile costruire una carta sul toro che consta di sette regioni, ciascuna confinante con le altre sei, e che quindi richiede sette colori.

L'immersione in una superficie orientabile permette di considerare una carta in modo combinatorio, cioè indipendente dalla struttura topologica, facendo entrare in gioco la teoria delle permutazioni nel modo che viene illustrato di seguito.

Un grafo è dato da un insieme di incidenze vertici-archi, due per ogni arco.Se il grafo ha n archi numeriamo con le cifre da 1 a 2n queste incidenze; per ogni vertice, uno dei due orientamenti possibili della superficie induce allora una permutazione circolare delle cifre relative alle incidenze a quel vertice.L'insieme di questi cicli è una permutazione σ di 51, 2,…, 2n6, scritta nella sua decomposizione in cicli.Si ha un'altra permutazione α, questa volta spezzata in cicli di lunghezza 2, data dalle coppie di cifre sugli archi.Il fatto che il grafo sia connesso (se non lo è non è possibile un'immersione nel senso richiesto) implica che il gruppo generato da queste due permutazioni è transitivo (da ogni cifra i si può passare a ogni altra cifra j applicando un numero conveniente di volte le due permutazioni). È notevole il fatto che per rappresentare le facce della carta sia ora sufficiente considerare il prodotto delle due permutazioni α e σ. Si ha infatti che, applicando α a una cifra di un arco e, si passa al vertice opposto su e; applicando poi σ si ruota nel senso dell'orientamento prescelto per finire su un arco e9 che limita una faccia limitata anche da e. Proseguendo in questo modo si ottiene un ciclo che rappresenta una delle facce, e così per tutte le altre facce.I tre elementi di un grafo immerso, rappresentati da vertici, archi e facce, si ottengono così in modo puramente algebrico-combinatorio.

Viceversa, un grafo si può definire come dato da una coppia di partizioni p₁ e p₂ di un insieme finito B con un numero pari di elementi, con la condizione che le classi di p₂ abbiano tutte due elementi.Le classi di p₁ danno i vertici, quelle di p₂ gli archi, due vertici u e v essendo collegati da un arco 5i, j6 se u contiene i e v contiene j (o viceversa).Il grafo è connesso se ogni unione di classi dei due tipi è tutto l'insieme B.Nel caso connesso, ordinando le cifre nelle classi di p₁ si ottiene una permutazione σ di B, spezzata in cicli, e ciò determina un'immersione del grafo in una superficie di un dato genere (α è automaticamente determinata dato che p₁ ha tutte classi con due elementi).Il genere si può determinare a partire solo da σ e α: denotando con z(γ) il numero di cicli di una permutazione γ (contando anche i cicli di lunghezza 1) si può infatti dimostrare che z(σ)2z(α)1z(σα)#2, e che inoltre la somma a primo membro è un numero pari.Si ha dunque, per un certo intero g, una formula di tipo Eulero: z(σ)2z(α)1z(σα)5222g, e g è precisamente il genere della superficie nella quale si può immergere il grafo in modo che l'orientamento induca attorno ai vertici la permutazione σ. Per costruire la superficie si considerano tanti poligoni (che sono omeomorfi a dischi) quanti sono i cicli del prodotto ασ, numerando i lati con le cifre del ciclo e in quell'ordine, e incollando poi (topologia quoziente) i lati di due poligoni quando le due cifre che questi portano appartengono a un ciclo di α. Tutti i possibili modi di orientare le classi della prima partizione danno luogo, eventualmente con ripetizione, a tutti i possibili generi di superfici nelle quali il grafo ammette un'immersione.Per es., il grafo completo con quattro vertici K₄ ammette un'immersione nella sfera (g50), due nel toro (g51) e nessuna immersione in superfici di genere maggiore.

Questo modo di rappresentare le carte permette inoltre di trasformare operazioni sulle carte in operazioni algebriche: per es., la soppressione di un arco 5i, j6 si ottiene moltiplicando α per la trasposizione (i, j). Si osserva poi un sorprendente legame con la teoria delle superfici di Riemann, in particolare per quanto riguarda gli automorfismi.Un automorfismo di una carta è una permutazione di B che conserva i cicli di σ e α, e dunque permuta con σ e α. Se A è il gruppo di tutte queste permutazioni, si può definire una carta quoziente rispetto ad A e dedurre una formula di Riemann-Hurwitz analoga a quella che sussiste nel caso classico delle superfici di Riemann: 2g225|A|(2γ22)1∑χ(x), x[A, dove γ è il genere della carta quoziente e χ(x) il numero dei cicli di σ, α e σα fissati da x.Per g50 (e dunque γ50), si trova che un automorfismo ammette esattamente due punti fissi, e di qui si deduce che A è necessariamente uno dei gruppi poliedrali: C_n (ciclico di ordine n, per ogni n), D_n (diedrale di ordine n, per ogni n), A₄ (gruppo alterno su 4 elementi), S₄ (gruppo simmetrico su 4 elementi), A₅ (gruppo alterno su 5 elementi), i gruppi cioè dei cinque solidi platonici.Come nel caso classico si deduce, per g$2, una maggiorazione per l'ordine del gruppo di automorfismi: |A|#84(g21) (il numero 84 dipende dal fatto che il massimo valore minore di 1 della somma degli inversi di tre numeri naturali è 41/42, valore che si ottiene per la terna 2, 3 e 7).

In un grafo, vertici e archi intervengono in modo asimmetrico, e lo stesso accade per vertici, archi e facce di una carta. Quest'asimmetria scompare lasciando cadere l'ipotesi che una delle due partizioni abbia le classi di cardinalità due; si ha così un ipergrafo, e introducendo un ordine nelle classi si ottiene una coppia di permutazioni (σ, α) che generano un gruppo transitivo.Il genere si definisce come sopra (la formula diventa z(σ) 1 z(α) 1 z(σα) 5 |B| 1 2 2 2g, e vale ancora la formula di Riemann-Hurwitz). Si ha così un'ipercarta: la rappresentazione su una superficie avviene considerando due famiglie di insiemi chiusi disgiunti omeomorfi a dischi, corrispondenti agli ipervertici σ e agli iperarchi α, e tali che un insieme di una famiglia incontri in un numero finito di punti gli insiemi dell'altra. Questi punti costituiscono l'insieme B, e sono disposti lungo le frontiere degli insiemi delle due famiglie nell'ordine dato dai cicli delle due permutazioni.Il complementare sulla superficie di queste due famiglie è un'unione di dischi aperti, le facce, le quali corrispondono ai cicli del prodotto ασ. È chiaro allora che la distinzione tra vertici, archi e facce non ha più luogo di esistere: l'ipercarta è rappresentata altrettanto bene dalla coppia (α, σ) come dalla (α, ασ) o dalla (σ, ασ).

Per le superfici non orientabili la caratteristica di Eulero vale 22n per la somma topologica di n piani proiettivi, 122n per la somma di un piano proiettivo ed n tori e 22n per una bottiglia di Klein più n tori.Il genere è dato da g522χ.Si osservi che la sfera e la bottiglia di Klein, una orientabile e l'altra no, hanno entrambe caratteristica 2.Per una carta su una superficie non orientabile il numero di colori richiesto è lo stesso del caso orientabile (anche qui fa eccezione il caso g50: per la bottiglia di Klein il numero è 6).Una costruzione, dovuta a W.T. Tutte, la quale fa intervenire tre trasposizioni invece delle due permutazioni σ e α, permette di trattare l'immersione di grafi in superfici non orientabili.

La classificazione dei gruppi finiti

La classificazione dei gruppi finiti offre un'ottima chiave di lettura per seguire lo sviluppo della teoria dei gruppi (v. gruppo, XVII).Si possono cioè vedere molti teoremi di struttura come strumenti che permettono di escludere certi casi come impossibili e di ridurre di molto i casi da considerare.In un articolo del 1895 pubblicato sulla rivista Mathematische Annalen, L.O.Hölder tracciò quello che in seguito venne chiamato programma di Hölder per la determinazione di tutti i gruppi finiti. Questo programma si basa sulla nozione di serie di composizione: vogliamo spiegare questo concetto sfruttando un'analogia con i numeri interi. Per ogni intero n esiste una successione di interi n₁.n₂.….n_r₋₁.n_r51 tale che ciascuno divide il precedente e i quozienti n_i/n_i₊₁ sono numeri primi. Gli n_i non sono univocamente determinati da n, ma lo sono invece (a meno dell'ordine in cui compaiono) i numeri primi n_i/n_i₊₁. L'intero n determina così un insieme di numeri primi e viceversa questo insieme determina n; tale risultato non è che un modo di esprimere il teorema fondamentale dell'aritmetica. Il risultato corrispondente in teoria dei gruppi è il teorema di Jordan-Hölder: in un gruppo finito si può costruire una successione G.G₁.G₂….G_r₋₁.G_r5516, dove G_i è un sottogruppo normale nel precedente G_i₋₁ e tale che i quozienti G_i₋₁/G_i siano gruppi semplici.Ricordiamo che un gruppo si dice semplice se non ha sottogruppi normali propri; il concetto di gruppo semplice è l'equivalente nella teoria dei gruppi di quello di numero primo nell'aritmetica.Una tale successione prende il nome di serie di composizione, e i quozienti G_i₋₁/G_i quello di fattori di composizione. Anche qui i sottogruppi G_i non sono univocamente determinati, ma i quozienti sì, nel senso che si ottengono quozienti che, a meno dell'ordine, sono isomorfi. C.Jordan aveva dimostrato che, per ogni serie, i quozienti G_i₋₁/G_i hanno, sempre a meno dell'ordine, la stessa cardinalità, mentre la dimostrazione che essi siano addirittura isomorfi è dovuta a Hölder.Ogni gruppo finito determina così, in modo univoco, un insieme di gruppi semplici.Dato allora un insieme di gruppi semplici H₁, H₂,…, H_r₋₁, ci si pone il seguente problema: è possibile determinare tutti i gruppi finiti che li ammettono come fattori di composizione? A questo scopo occorre risolvere il problema dell'ampliamento: dati due gruppi K e Q, determinare tutti i gruppi G che ammettono un sottogruppo normale isomorfo a K e tali che il quoziente G/K sia isomorfo a Q; un tale gruppo G si dirà ampliamento di K mediante Q. Questo problema è stato oggetto di ricerca negli anni Venti del 20° sec., soprattutto per opera di O.Schreier. La tecnica da lui sviluppata permette di costruire in modo sistematico tutti gli ampliamenti G di K mediante Q, nel senso che si ottengono le tavole di moltiplicazione dei vari G; tuttavia, nella lista dei gruppi che così si ottiene, uno stesso gruppo può apparire più volte, restando aperto in questo modo il problema di stabilire se due gruppi sono isomorfi o meno.A partire da un insieme di gruppi semplici H₁, H₂,…, H_r₋₁, in quest'ordine, si possono allora determinare tutti i gruppi che li ammettono come fattori di composizione costruendo un albero, i cui vertici sono gli ampliamenti che successivamente si ottengono. I rami costituiscono le possibili serie di composizione, mentre i vertici estremi rappresentano i gruppi cercati.Si vede così che i gruppi semplici sono i 'mattoni' per mezzo dei quali si possono costruire tutti i gruppi finiti. Si può dunque riassumere il programma di Hölder in questi due punti: 1) determinare tutti i gruppi semplici; 2) risolvere il problema dell'ampliamento.

L'idea di considerare serie di composizione nasce, come la nozione stessa di gruppo, nel contesto della teoria di Galois. Nello studio dell'equazione generale di quinto grado E. Galois fece la prima scoperta in questo senso: il più piccolo gruppo semplice di ordine non primo contiene 60 elementi, risultato che egli enunciò senza dimostrazione. Si tratta sempre, nelle ricerche del tempo di Galois, e per un certo periodo anche in quelle degli studiosi successivi, di gruppi di permutazioni, in quanto l'interesse dei ricercatori era diretto, oltre che al problema della risoluzione delle equazioni in una variabile, allo studio delle funzioni razionali in più variabili.La semplicità del gruppo alterno A_n per ogni n.4, dimostrata da Jordan (1870), è uno dei risultati più importanti della teoria. Dal punto di vista della classificazione, la classe degli A_n costituisce storicamente la prima classe infinita di gruppi semplici non abeliani.Intorno agli stessi anni, É.-L.Mathieu scoprì l'esistenza di cinque gruppi di permutazioni che W.Burnside all'inizio del 20° sec. definì sporadici, non appartenenti cioè a una classe infinita.Si noti che è stato necessario attendere circa un secolo per la scoperta di un nuovo gruppo sporadico: il gruppo J₁ di Z.Janko, nel 1965. In un altro ordine di idee, Jordan diede inizio alla sistemazione di vari risultati concernenti una classe di gruppi dai quali si possono ottenere gruppi semplici: i cosiddetti gruppi lineari sopra un campo finito di ordine q.Si ottiene così una nuova classe infinita di gruppi semplici, quelli che oggi si denotano con L_n(q) (gli L_n(q) sono tutti semplici esclusi i gruppi L₂(q), per |q|52 o 3).Infine, da un punto di vista più astratto si è affrontato il problema della classificazione cercando di stabilire per quali n possano esistere gruppi semplici di ordine n.Se per alcuni valori di n bastano mezzi molto elementari, per altri occorrono strumenti più sofisticati.Bisogna però attendere la seconda metà del Novecento per assistere a passi avanti significativi nel problema della classificazione. R.Brauer, in un intervento al Congresso internazionale dei matematici tenutosi ad Amsterdam nel 1954, presentò un nuovo programma di attacco al problema.

Da un punto di vista estremamente generale si tratta di questo: dato un gruppo H, si vogliono determinare tutti i gruppi semplici G che contengono H come sottogruppo facendo ipotesi sul modo in cui H è contenuto in G.Si può richiedere per es. che H sia massimale in G, o se è un p-gruppo, che H sia un p-Sylow di G e così via. Il problema è quello di restringere le possibilità per un gruppo G soggetto a date condizioni. L'idea di Brauer fu quella di richiedere che H sia contenuto in G come centralizzante di un'involuzione (un'involuzione è un elemento di ordine 2 e il centralizzante di un elemento è il sottogruppo degli elementi che permutano con esso).Uno dei modi di procedere nello svolgimento del programma fu quello di considerare il centralizzante H di un'involuzione in un gruppo semplice noto G e di cercare quindi di caratterizzare G come l'unico gruppo semplice che ammette H come centralizzante di un'involuzione.Un aspetto sorprendente di questa ricerca fu la comparsa dei gruppi sporadici: Brauer dimostrò che per q.3, il gruppo L₃(q) è l'unico gruppo semplice che ammette GL₂(q) come centralizzante di un'involuzione, mentre per q53 compare, assieme a L₃(3), anche il gruppo di Mathieu M₁₁. Come naturale sviluppo di questa linea di ricerca ci si propose poi di caratterizzare i gruppi semplici assegnando come centralizzante non un singolo gruppo, ma un gruppo che avesse certe proprietà. Seguendo questo approccio M.Suzuki determinò tutti i gruppi semplici nei quali il centralizzante di ogni involuzione ha un 2-Sylow normale. Essi sono: 1) L₂(p), dove p.3 è un primo di Fermat o di Mersenne; 2) L₂(2ⁿ), n$2; 3) A₆; 4) L₃(q), PSU₃(q) e Sz(q), con q potenza di 2 (i gruppi Sz(q) sono particolari gruppi di matrici scoperti da Suzuki).

Visto il ruolo così particolare che svolge il numero primo 2, fu naturale pensare che prescrivendo un 2-Sylow si potesse, se non determinare il gruppo, almeno individuare una classe di gruppi suscettibili di una descrizione unitaria.Così, per es., se si prescrive come 2-Sylow il gruppo di ordine del tipo 4 di Klein si ottiene la famiglia dei gruppi L₂(q), q?5 e q;63 mod8.Come nel caso del centralizzante, si considerarono non singoli gruppi, ma famiglie di gruppi aventi determinate proprietà.Così, J.Walter nel 1969 classificò i gruppi semplici con 2-Sylow abeliano, che sono i seguenti: 1) L₂(q), q$5 e q;63 mod8; 2) L₂(2ⁿ), n$2; 3) gruppi del tipo di Ree; 4) il gruppo di Janko J₁ (i gruppi di Ree sono particolari gruppi del tipo di Lie). Anche qui compare un gruppo sporadico, il gruppo J₁. Se il 2-Sylow è diedrale, D.Gorenstein e J. Walter (1962) hanno dimostrato che si ottengono i gruppi L₃(q), q;3 mod4;PSU₃(q), q;1 mod4, più il solito gruppo di Mathieu. Ma il risultato più importante (che costituisce la premessa di tutta la messe di risultati ottenuti nel periodo che va dagli anni Sessanta alla conclusione dell'avventura della classificazione nei primi anni Ottanta) è la dimostrazione nel 1963, da parte di W.Feit e J.Thompson, della congettura di Burnside, secondo la quale un gruppo semplice ha ordine pari. Thompson, insignito della medaglia Fields nel 1970, è certamente la figura più eminente fra tutti i ricercatori di questo periodo; a lui è dovuta anche la lista dei gruppi semplici minimali, ottenuta alla conclusione di una lunga serie di articoli pubblicati nel corso di sette anni, dal 1968 al 1974. Questi gruppi sono i seguenti: 1) L₂(2^p), L₂(3^p), p primo qualunque; 2) L₂(p), p.3, e p;2 o 3 mod5; 3) Sz(2^p), p.2; 4) L₃(3).

Un altro esempio di classificazione di oggetti 'semplici' in algebra, legato alla nostra discussione, è quello delle algebre di Lie semplici di dimensione finita sui complessi, iniziata da W.K.J.Killing nel 1888 e completata da E.Cartan alla fine dell'Ottocento.Tra le algebre di Lie semplici vi sono quattro famiglie infinite, il cui ruolo è analogo a quello delle famiglie infinite di gruppi semplici, e cinque algebre eccezionali, che possono ricordare i cinque gruppi sporadici di Mathieu.C.Chevalley, in un lavoro della metà degli anni Cinquanta che ebbe un'enorme risonanza, considerò quelli che in seguito vennero chiamati gruppi di Chevalley.Egli dimostrò che data un'algebra di Lie semplice sui complessi e un campo K finito, esiste un gruppo di matrici su K (gruppo di Chevalley appunto) che è un gruppo semplice.R.Ree (1957) mostrò che la tecnica di Chevalley dava luogo ai gruppi classici (esclusi i gruppi unitari e alcuni gruppi ortogonali), e presto si vide come ottenere per questa via tutti i gruppi classici e nuove famiglie infinite di gruppi semplici.Tutti questi gruppi vanno sotto il nome di gruppi di tipo Lie.Infine J.Tits (1964) diede una dimostrazione di carattere generale della semplicità comprendente i gruppi lineari e i gruppi che provengono dalle algebre di Lie.

La comparsa di gruppi sporadici, se da un lato comportava una maggiore chiarezza perché ogni scoperta di un nuovo gruppo semplice permetteva di aggiungere un tassello alla costruzione del quadro, dall'altro era una fonte di incertezza in quanto la scoperta stessa del nuovo gruppo lasciava supporre che ce ne potessero essere altri: la non sistematicità di questa classe di gruppi metteva in pericolo l'esistenza di una classificazione completa.Il primo gruppo semplice sporadico del periodo moderno è quello di Janko, un gruppo di matrici 737 sul campo F₁₁ il cui ordine è 175.560. A Janko è poi dovuta la scoperta di altri tre gruppi semplici.Alla fine della classificazione, il numero dei gruppi sporadici ammontava a 26; il più piccolo (a parte quelli di Mathieu) è J₁, il più grande è il gruppo di Fischer F₁, che ha un numero di elementi dell'ordine di 10⁵⁴: per questo motivo F₁ è detto il mostro (the monster).Esso fu proposto nel 1973 da B.Fischer e, indipendentemente, da R.L.Griess; la determinazione della sua esistenza e unicità costituì l'ultimo atto della classificazione.Con la determinazione dei 26 gruppi sporadici la classificazione dei gruppi semplici è completa.La lista consta dei seguenti gruppi: 1) gruppi di ordine primo; 2) gruppi alterni; 3) gruppi del tipo di Lie; 4) gruppi sporadici.

È probabile che future ricerche facciano perdere ai gruppi sporadici un po' del loro carattere di eccezionalità.Quasi tutti sono infatti contenuti nel mostro F₁, e ci sono pertanto buone ragioni per pensare di poter arrivare a una descrizione coerente e unitaria di questi gruppi.

Una critica più o meno esplicita ha accompagnato le ricerche sui gruppi semplici ed è andata crescendo di intensità parallelamente all'affluire dei risultati. Essa sostiene che le dimostrazioni sono troppo lunghe e la dipendenza tra i vari risultati troppo stretta: ciò rende praticamente impossibile controllare i risultati nel dettaglio, anche da parte di specialisti che, forse proprio a causa di queste difficoltà, sono diventati via via un gruppo sempre più ristretto, quasi una setta.Il lavoro di Walter consta di 109 pagine, la classificazione di Thompson dei gruppi semplici minimali è lunga 410 pagine (tra l'altro distribuite in sette anni), la dimostrazione del teorema di Feit e Thompson occupa 250pagine, e così via.Non vi è la certezza che un errore, o anche una semplice svista, non abbia lasciato sfuggire qualche altro gruppo semplice.Certo, la lunghezza e l'intreccio tra i vari risultati sono segni delle difficoltà da superare e della complessità degli argomenti sviluppati.Ma è innegabile che questi aspetti rappresentino un serio inconveniente per l'accettazione dei risultati da parte della comunità scientifica, anche se il problema riguarda in modo più o meno profondo tutta la produzione matematica e più in generale tutta l'attività di ricerca.Si è di fronte a difficoltà analoghe a quelle che si presentano riguardo alle dimostrazioni che fanno uso del calcolatore e alle quali abbiamo accennato nel caso del problema dei quattro colori o del piano di ordine 10.

bibliografia

D. Knuth, The art of computer programming, Reading (Mass.) 1968-73, 1973-81².

M. Davis, Y.V.Matiyasevich, J.Robinson, Hilbert's tenth problem.Diophantine equations: positive aspects of a negative solution, in Proceedings of symposia in pure mathematics, 1976, 28, pp. 323-78.

T.L. Saaty, P.C. Kainen, The four-colour problem, New York 1977.

D. Gorenstein, Finite simple groups.An introduction to their classification, New York 1982.

A.K. Lenstra, H.W. Lenstra, L. Lovász, Factoring polinomials with rational coefficients, in Matematische Annalen, 1982, 261, pp. 515-34.

D. Barnette, Map coloring, polyhedra and the four-colour problem, Washington (D.C.) 1983.

C.W.C. Lam, L.Thiel, S. Swiercz, The nonexistence of finite projective planes of order 10, in Canadian journal of mathematics, 1989, 6, pp.1117-23.

R.L. Graham, B.L. Rothschild, J.H. Spencer, Ramsey theory, New York 1990.

V.Rödl, Some developments in Ramsey theory, in International congress of mathematicians, Kyoto 1990.

R. Cori, A. Machì, Maps, hypermaps and their automorphism: a survey, i, ii, iii, in Expositio mathematicae, 1992, 5, pp. 403-67.

Y.V. Matiyasevich, Hilbert's tenth problem, with a foreword by Martin Davis, Cambridge (Mass.) 1993.

Y.V. Matiyasevich, Some arithmetical restatements of the four-colour conjecture, Metz 1996.