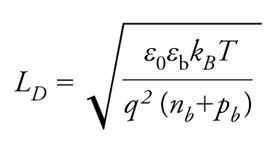Superfici, fisica delle
Superfici, fisica delle
La maggior parte dei solidi presenta una struttura cristallina nella quale gli atomi sono disposti nei vertici di un reticolo periodico tridimensionale. Fanno eccezione i materiali amorfi e i vetri, che assomigliano piuttosto a liquidi solidificati. Nel seguito ci occuperemo prevalentemente dei solidi cristallini, quelli tra l’altro che rivestono il maggiore interesse tecnologico.
In un solido reale la periodicità del reticolo è interrotta dalla presenza della superficie. In linea di principio la struttura di una superficie dovrebbe coincidere con quella di un piano reticolare sottostante, ma di fatto ciò non avviene per vari motivi, tra cui ricordiamo: (a) sulla superficie, più facilmente che nell’interno del solido, esistono difetti (gradini, isole, pozzi ecc.) che tendono a romperne la periodicità o addirittura a renderla disordinata; (b) la superficie è spesso contaminata da impurezze chimiche provenienti dall’ambiente esterno o dall’interno del solido (il cosiddetto bulk) tramite un processo di segregazione superficiale; (c) gli atomi di superficie godono di una maggior libertà di movimento e sono soggetti a forze assai diverse che nel bulk. Si osserva spesso un rilassamento superficiale (il piano di superficie rilassa verso il piano sottostante) o in molti casi una vera e propria ricostruzione superficiale nella quale gli atomi si dispongono nei vertici di un reticolo bidimensionale diverso da quello dei piani sottostanti. In molti casi anche gli atomi estranei adsorbiti o chemisorbiti sulla superficie si dispongono in strutture regolari, spesso con periodicità diversa da quella dei piani sottostanti.
La ricostruzione provoca a sua volta una modifica della struttura e delle proprietà elettroniche superficiali che sono poi quelle che determinano molte proprietà fisiche, chimiche e tecnologiche del solido. È necessario sottolineare subito che, dal punto di vista storico, è stato proprio l’effetto degli stati elettronici di superficie sulle proprietà di trasporto degli elettroni nei transistori ad aver stimolato, a partire dagli anni Cinquanta, il grande sviluppo sia scientifico sia applicativo della fisica delle superfici solide. Gli stati elettronici di superficie erano stati previsti teoricamente per un semplice modello unidimensionale da Igor Tamm (1932) e per un modello più realistico, suscettibile di applicazione ai semiconduttori, da William B. Shockley (1939). In questi modelli teorici gli stati superficiali sono essenzialmente dovuti alla terminazione del potenziale periodico sulla superficie del solido. L’energia associata a tali stati spesso cade in una banda proibita del solido non limitato. È proprio questo fatto, che associa alla superficie nuovi livelli di energia, a modificare, talvolta drasticamente, le proprietà elettroniche del solido, soprattutto nel caso dei semiconduttori.
Le soluzioni tecnologiche associate al funzionamento dei transistori hanno stimolato un grande avanzamento delle conoscenze della struttura microscopica delle superfici. Si è cioè verificato un processo nella direzione di un avanzamento tecnologico verso la scienza di base in senso opposto a quanto avviene comunemente.
Gli stati di superficie e l’invenzionedel transistore
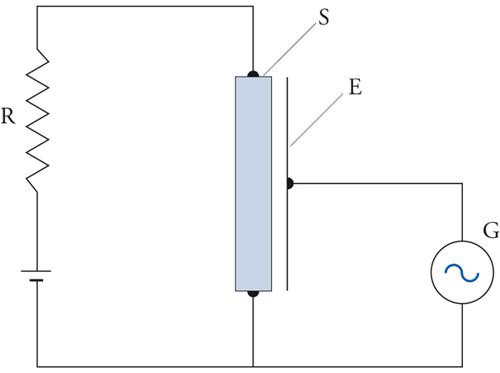
È interessante ricordare che il rudimentale transistore realizzato nei laboratori della Bell Thelephone di Murray Hill verso la fine della prima metà del secolo scorso, per ragioni apparentemente inspiegabili, non funzionò. Tale dispositivo, ideato nel 1948, da Shockley e Gerald L. Pearson, è mostrato schematicamente nella fig. 2. L’applicazione di un segnale alternato (o impulsivo) tramite il generatore G non richiede l’uso di potenza elettrica in quanto la differenza di potenziale è applicata ai capi del condensatore costituito dal semiconduttore S e dall’elettrodo metallico E. Il campo elettrico generato in tal modo nella regione superficiale del semiconduttore richiama (o respinge) elettroni che finiscono per muoversi in una specie di canale superficiale, modificando la resistenza elettrica del semiconduttore e conseguentemente la corrente che scorre nella resistenza esterna R. Ai capi di R si può misurare il segnale di uscita amplificato.
La spiegazione del mancato funzionamento fu data da John Bardeen sulla base di un lavoro precedente (1947) in cui era discusso l’effetto degli stati di superficie sulla conducibilità elettrica dei semiconduttori: gli elettroni del canale superficiale sono intrappolati negli stati di superficie e non contribuiscono alla conducibilità del campione, rendendo impossibile il funzionamento del dispositivo. L’insieme di questi lavori portò tuttavia alla realizzazione del primo transistore funzionante da parte di Bardeen e Walter H. Brattain (1948) che aprì una nuova era nell’elettronica e nella nostra civiltà dell’informazione.
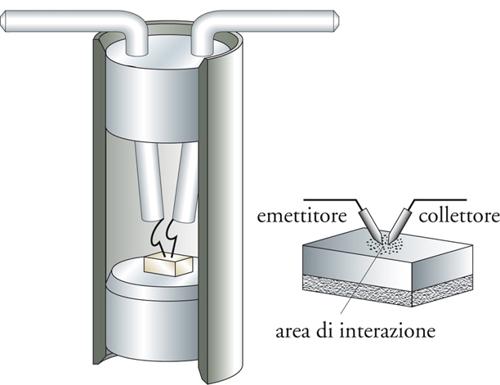
Il primo transistore (chiamato di tipo A) con contatti metallo-semiconduttore semplicemente pressati contro la superficie di un cristallo di germanio (i cosiddetti baffi di gatto o catwhiskers) è mostrato in fig. 3. Esso ricorda nella sua struttura gli storici coherer delle radio a galena o più precisamente i raddrizzatori a cristallo di silicio che rimasero in uso nelle telecomunicazioni fino alla fine della Prima guerra mondiale. Essi comunque, con modifiche e implementazioni, fanno ancora parte del patrimonio tecnologico attuale e vengono chiamati diodi Schottky.
Il transistore di tipo A era tuttavia un dispositivo poco affidabile, difficilmente miniaturizzabile, che non avrebbe potuto competere con i tubi elettronici che, seppure ingombranti e grandi dissipatori di potenza, erano all’epoca dispositivi tecnologicamente molto avanzati. Esso venne però subito sostituito da un dispositivo molto più piccolo e affidabile, il transistore a giunzione o bipolare, sviluppato, sempre presso i laboratori Bell, da Shockley nel 1949. Tale transistore era costituito dall’unione di due giunzioni p-n, ossia da una struttura n-p-n (o p-n-p) essenzialmente planare e perciò adatta alla grandissima integrazione presente nei moderni circuiti integrati. Come è noto, una giunzione n-p (p-n) è costituita dall’unione (a livello atomico) di un materiale n (nel quale la conduzione è dovuta a elettroni negativi) con un materiale p (nel quale la conduzione è dovuta a carenza di elettroni ossia a lacune positive). I due tipi di materiali sono ottenuti dal cristallo ideale mediante l’aggiunta di droganti costituiti da atomi di valenza superiore o inferiore a quella della matrice: nel silicio tetravalente, per esempio, l’aggiunta di As pentavalente dà origine a un eccesso di elettroni, ossia a un materiale n, mentre l’aggiunta di B trivalente produce a una carenza di elettroni, ossia un materiale p. Nelle giunzioni gli elettroni passano dal materiale n a quello p formando, all’interfaccia, un doppio strato di carica che genera una barriera di potenziale tra i due materiali. L’effetto è simile alla differenza di potenziale di contatto tra due metalli diversi scoperta da Alessandro Volta nel 1797 con una serie di esperimenti.
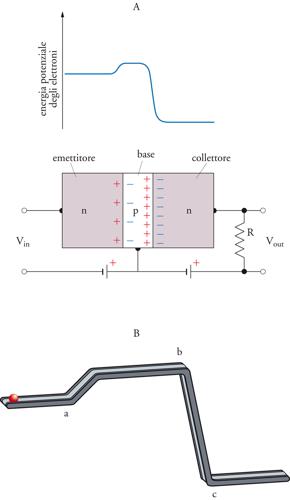
Nel transistore la prima giunzione viene polarizzata da una differenza di potenziale esterna di segno tale da ridurre l’altezza della barriera, mentre la seconda giunzione viene polarizzata in modo da aumentarla. La parte centrale tra le due giunzioni (chiamata base) deve avere uno spessore così piccolo (inferiore alla lunghezza di ricombinazione elettrone-lacuna) da permettere che gli elettroni (in un transistore n-p-n) possano attraversare la base di tipo p senza subire processi di ricombinazione che ne ridurrebbero il numero; si ha cioè approssimativamente la stessa corrente attraverso le due giunzioni. La fig. 4A mostra lo schema elettrico (nel caso di un transistore n-p-n ) e indica la nomenclatura convenzionale per le tre regioni: emettitore, base, collettore. L’energia potenziale degli elettroni è indicata nella parte superiore della figura. Una resistenza in serie al collettore permette, se dimensionata, di ottenere un’amplificazione di tensione e di potenza. Il transistore a giunzione, o bipolare, è tuttora molto usato, specie nei dispositivi di potenza.
Il funzionamento del transistore è bene illustrato da un modello meccanico mostrato schematicamente in fig. 4B. Su una guida metallica, con un profilo come quello della figura, può muoversi, con attrito trascurabile, una biglia o un carrello. Una piccola spinta data alla biglia (che si trova inizialmente alla sinistra di a) le permette di superare la barriera in a e di raggiungere il punto c avendo acquistato una notevole energia cinetica. Nel modello meccanico tale aumento è ottenuto a spese dell’energia potenziale gravitazionale mentre nel transistore avviene a spese dell’energia elettrica fornita dai generatori esterni. Si può anche evidenziare un’ulteriore analogia: se il tratto ab (corrispondente alla base nel transistore) fosse molto lungo la biglia finirebbe per perdere, per attrito, la sua energia cinetica e non raggiungerebbe mai il punto b (e c). In un certo senso anche il transistore di tipo A può essere pensato come la successione di due giunzioni metallo-semiconduttore. L’area attiva tra le due punte rappresenta la base. Per un corretto funzionamento è necessario che la distanza tra le punte sia più piccola della lunghezza di ricombinazione elettrone-lacuna nel semiconduttore, analogamente a quanto richiesto per lo spessore della base nel transistore a giunzione.
La presenza di stati elettronici di superficie nella regione della base ancora una volta poneva dei problemi: era possibile, per esempio, che in un transistore p-n-p la base n presentasse, a causa di tali stati, caratteristiche superficiali di tipo p creando un canale che cortocircuitava le due giunzioni impedendo il funzionamento del transistore. Era perciò necessario comprendere e controllare le proprietà superficiali dei semiconduttori per poter procedere allo sviluppo della moderna elettronica dello stato solido.
Gli stati di superficie associati alle imperfezioni o alla contaminazione potevano essere controllati migliorando il trattamento meccanico di pulitura abrasiva e il successivo attacco chimico (etching) che asporta la parte danneggiata meccanicamente, oppure tramite bombardamento ionico e susseguente ricottura (annealing). Al contrario, gli stati associati alla diversa disposizione degli atomi superficiali erano difficilmente controllabili, trattandosi di processi intrinseci alla superficie stessa.
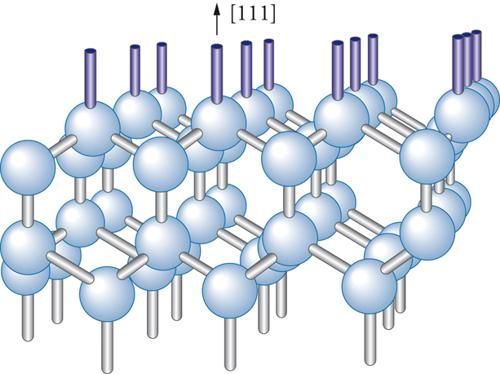
Ci si accorse comunque che questi stati erano associati prevalentemente all’esistenza di legami chimici non saturi sulla superficie. Nel caso del Si e del Ge, semiconduttori covalenti del IV gruppo che cristallizzano nella struttura del diamante, esistono, per esempio, uno o due legami non saturati per atomo di superficie: uno per la superficie (111) e due per quella (100). Si tratta dei cosiddetti legami pendenti (DB, Dangling bond) mostrati nella fig. 5 per la superficie (111) del Si.
Per neutralizzare questi legami è necessario ossidare in modo controllato la superficie creando uno strato di pochi piani reticolari di ossido di Si con un processo chiamato passivazione. Il biossido di silicio è un ottimo isolante anche se la sua struttura in superficie è tuttora controversa.
Il controllo dei processi di passivazione permise di trasformare il dispositivo della fig. 2 usando l’ossido stesso del semiconduttore come dielettrico nel condensatore tra semiconduttore ed elettrodo metallico. Il dispositivo funzionò, come dimostrarono nel 1960 D. Khang e Martin M. Atalla, e costituì il prototipo di quello che viene ora chiamato MOSFET (Metal oxide semiconductor field effect transistor), oppure più semplicemente MOS. La spiccata planarità insita nella struttura geometrica del MOS, evidente dalla fig. 2, ha permesso di inserire nei circuiti integrati alcune decine di milioni di transistori su un singolo chip (area dell’ordine del cm2) rendendo possibile la straordinaria potenza di calcolo dei moderni elaboratori.
Le varie fasi del processo concettuale che sta alla base del funzionamento del MOSFET sono illustrate in modo elementare e schematico nella Tavola I. Può essere interessante notare che tra l’esperimento che ha verificato il mancato funzionamento del dispositivo della fig. 2 e l’invenzione del MOSFET trascorsero ben tredici anni. Ancora più interessante, e in un certo qual mo-do sorprendente, è l’osservazione che già negli anni Trenta esistevano brevetti che enunciavano il principio di funzionamento del MOSFET (Julius E.Lilienfeld, U.S. Patent No 1.745.175 del 1930; O. Heil, British Patent No 439.475 del 1935). La mancanza di un’adeguata tecnologia, la scarsa caratterizzazione dei materiali, l’inesistenza di sia pur rudimentali nozioni di fisica delle superfici hanno però ritardato di trent’anni questa importante invenzione; tale ritardo evidenzia il fatto che nella moderna tecnologia spesso non è tanto importante l’idea (conceptual design) quanto la capacità di realizzarla praticamente, il cosiddetto know how.
La struttura delle superfici dei cristalli
Qui ci limiteremo a considerare in modo elementare il problema della ricostruzione superficiale che, nella sua varietà e complessità, è molto interessante e ha stimolato negli ultimi anni una cospicua attività di ricerca che ha prodotto alcuni risultati significativi. Dal punto di vista simbolico, il tipo di ricostruzione superficiale viene indicato facendo seguire agli indici di Miller del piano cristallografico la notazione m×n dove m e n sono in generale (ma non sempre) interi positivi che indicano i rapporti tra i lati della cella elementare della superficie ricostruita e quelli della superficie ideale. Per esempio, Si(111)2×1 significa che sulla faccia (111) del Si la cella elementare ha una lunghezza doppia in una delle due direzioni cristallografiche primitive mentre rimane invariata nell’altra. Qualora la cella elementare della superficie ricostruita risulti ruotata di un angolo α rispetto a quella ideale si fa seguire Rα alla notazione precedente.
Dal punto di vista sperimentale un notevole progresso si ebbe negli anni Sessanta con lo sviluppo della tecnologia dei vuoti ultraspinti (UHV, Ultra high vacuum), che permisero di osservare e manipolare le superfici in ambienti con pressioni inferiori a 10−10 tor (ca. 1013 volte minori della pressione atmosferica). Le superfici ottenute e manipolate in UHV furono chiamate superfici pulite per distinguerle dalle superfici reali di interesse esclusivamente tecnologico.
Per osservare a livello atomico la struttura delle superfici pulite vengono spesso usate due tecniche specifiche che hanno una grande sensibilità per la posizione degli atomi nei primissimi piani del cristallo: la diffrazione di elettroni lenti (LEED, Low energy electron diffraction) e la microscopia a effetto tunnel (STM, Scanning tunneling microscopy). Vengono tuttavia usate molte altre tecniche, quali la fotoemissione risolta in angolo (ARUPS, Angle resolved ultraviolet photoemission), le tecniche ottiche, la diffrazione di elettroni di alta energia, la diffrazione dei raggi X, lo scattering di ioni positivi e così via.
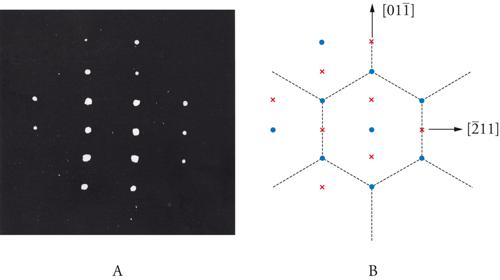
Nel LEED vengono osservati i diagrammi di Laue dovuti alla diffrazione di elettroni di energia compresa tra 10 e 100 eV che, penetrando poco nel solido, ne esplorano unicamente i primi piani reticolari. Un esempio significativo è mostrato nella fig. 6, dove è riportato il diagramma LEED nel caso di una superficie di Si sfaldato in UHV. Nella fig. 6B è riportato con circoletti pieni il diagramma che ci si aspetterebbe per una superficie non ricostruita (1×1) e con crocette le macchie extra osservate sperimentalmente. Si vede che nella direzione [01¯1] la dimensione della cella elementare è raddoppiata. Si deve osservare che i diagrammi di Laue sono osservati nello spazio reciproco (2π/λ, con λ lunghezza d’onda dell’elettrone). Il dimezzamento delle distanze nella direzione [01¯1] dello spazio reciproco corrisponde cioè a un raddoppio della cella elementare nello spazio reale; si osserva cioè una ricostruzione 2×1.
Nel microscopio a scansione a effetto tunnel una punta metallica (molto sottile, ma di dimensioni pur sempre macroscopiche) viene fatta scorrere in prossimità della superficie da esaminare a una distanza inferiore a 10-7 cm. Gli elettroni passano, per effetto tunnel, tra la punta e il campione dando origine a una corrente (dell’ordine di 10-9 A) tanto più grande quanto più la punta è vicina all’atomo di superficie. La dipendenza della corrente dalla distanza è di tipo esponenziale, e questo fa in modo che la corrente provenga prevalentamente dall’atomo che sta immediatamente sotto la punta. Un sistema elettronico mantiene costante la corrente avvicinando o allontanando la punta dal campione tramite un dispositivo piezoelettrico. La tensione applicata a tale dispositivo dà immediatamente la rugosità della superficie su scala atomica. I dati sono elaborati da un computer che fornisce un’immagine bidimensionale della superficie. Un esempio tipico è mostrato nella fig. 7 dove viene riportata l’immagine STM di Au(111)23×1 .
Il fenomeno della ricostruzione è molto vario e complesso. A tuttora non esiste un’unica teoria che riesca a inquadrare correttamente tutte le ricostruzioni osservate sperimentalmente. Si può affermare genericamente che nei semiconduttori covalenti la ricostruzione tende a minimizzare il numero dei legami superficiali non saturati (DB). Poiché nei legami sp3 tipici dei semiconduttori covalenti l’energia associata agli angoli tra i legami è esigua rispetto a quella associata alla lunghezza dei legami, laricostruzione avviene spesso con spostamenti degli atomi che conservano approssimativamente le reciproche distanze ma non gli angoli tra i legami. Un esempio interessante è quello della ricostruzione 7×7 della faccia (111) del Si, illustrata nella Tav. II.
Nei metalli, le energie (negative) associate alle ricostruzioni sono più piccole che non nei semiconduttori. Il legame metallico, infatti, è assai poco localizzato e in conseguenza l’energia superficiale dipende poco dalla posizione degli atomi. Questo fa sì che nei metalli la ricostruzione si riscontri più raramente. Le interazioni repulsive tra gli atomi favoriscono tuttavia la formazione di superfici rilassate o ricostruzioni con celle elementari molto grandi come quella mostrata nella fig. 7. In qualche caso l’interazione repulsiva può provocare l’espulsione di intere file di atomi, come per esempio in Au(110)2×1 o Pt(110)2×1, denominate ricostruzioni con fila mancante (missing row).
Dal punto di vista teorico, un notevole avanzamento si è avuto nel 1985 con l’introduzione del metodo di Car-Parrinello che, pur avendo applicazione generale, si è dimostrato particolarmente efficace nel calcolo della struttura delle superfici. Questo metodo consiste nel simulare l’evoluzione temporale di un insieme di alcune centinaia di atomi, a partire da uno stato iniziale come, per esempio, la superficie ideale. L’energia (o meglio l’energia libera) dell’insieme dipende dalla posizione reciproca degli atomi. Operando una variazione virtuale di tali posizioni e calcolando per ciascuna configurazione l’energia totale, è possibile ottenere la forza che agisce sui singoli atomi per mezzo del teorema di Hellmann-Feynman della meccanica quantistica e ottenere l’evoluzione dinamica dell’insieme. Il teorema di Hellmann-Feynman è infatti la generalizzazione quantomeccanica del ben noto teorema di meccanica classica che lega la forza alle derivate dell’energia potenziale. Il metodo richiede elevate potenze di calcolo ed è di difficile applicazione quando la cella elementare della superficie ricostruita contiene un gran numero di atomi.
I metodi come quello descritto vengono chiamati ab initio (o da principi primi), per evidenziare che non vengono fatte ipotesi ad hoc nel calcolo delle strutture.
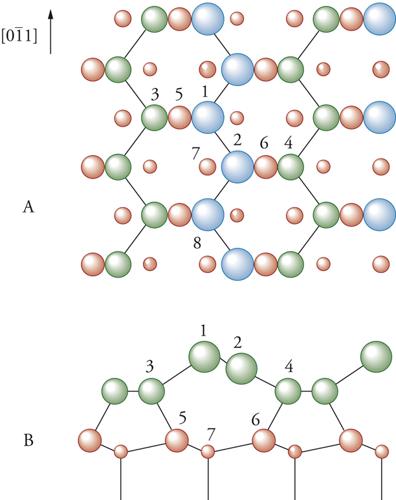
Un’applicazione particolarmente significativa è stata fatta da Roberto Car, Michele Parrinello e collaboratori (1990) con il calcolo del modello di ricostruzione 2×1 della superficie (111) del silicio. Questa superficie è stata oggetto di molti studi teorici e sperimentali che si sono concretizzati in un modello a catene con legami π (π-bonded chain model) proposto da K.C. Pandey nel 1981 e mostrato nella fig. 8, dove le catene a zig-zag sono quelle che includono gli atomi 1,2,8 e così via. Il modello è stato confermato da molti dati sperimentali, tra cui la grande anisotropia delle transizioni ottiche associate ai DB, i risultati sullo scattering di ioni e l’osservazione diretta con il microscopio STM.
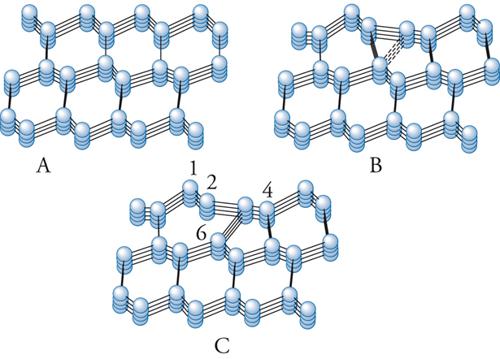
Anche se il modello era già consolidato, ciò nondimeno l’applicazione, nel 1990, del metodo di Car-Parrinello alla superficie del Si(111)2×1 è risultata importante in quanto ha dimostrato la possibilità di ottenere direttamente da principi primi la struttura di una superficie ricostruita. In particolare, il calcolo ha risolto una controversia sollevata molte volte e cioè che la struttura della fig. 8 comporta, per ragioni topologiche, la rottura di almeno un legame; un processo che, in linea di principio, dovrebbe richiedere una considerevole quantità di energia. La dinamica della ricostruzione, riportata nella fig. 9, mostra tuttavia che la transizione avviene gradualmente (in modo adiabatico) dallo stato iniziale A allo stato finale C, con una piccola energia di attivazione.
Il metodo di Car-Parrinello ha avuto moltepliciapplicazioni, tra cui le più recenti nello studio dei processi catalitici in fase gassosa. Il problema della catalisi è strettamente legato alla fisica e chimica delle superfici. Infatti l’esistenza sulle superfici reali di gradini e piegature (come mostrato nella fig. 1) può servire a immobilizzare una delle molecole reagenti rendendo più facile la combinazione con l’altro partner della reazione. Inoltre la diversa posizione del livello di Fermi in superficie e/o in prossimità di difetti può fare in modo che la molecola intrappolata si comporti da donatore o accettore di elettroni favorendo o ostacolando la reazione catalitica.
Bibliografia
Ancillotto 1990: Ancillotto, Francesco e altri, Structural, electronic, and vibrational properties of Si(111)-2x1 from abinitio molecular dynamics, “Physical review letters”, 65, 1990, pp. 3148-3151.
Bardeen 1947: Bardeen, John, Surface states and rectification at a metal semi-conductor contact, “Journal of physics review”, 71, 1947, pp. 717-727.
Bardeen, Brattain 1948: Bardeen, John - Brattain, Walter H., The transistor, a semi-conductor triode, “Physical review”, 74, 1948, pp. 230-231.
Barth 1990: Barth, Johannes V. e altri, Scanning tunneling microscopy observations on the reconstructed Au(111) surface: atomic structure, long-range superstructure, rotational domains, and surface defects, “Physical review”, B42, 1990, pp. 9307-9318.
Car, Parrinello 1985: Car, Roberto - Parrinello, Michele, Unified approach for molecular dynamics and density-functional theory, “Physical review letters”, 55, 1985, pp. 2471-2474.
Chiaradia 1984: Chiaradia, Pietro e altri, Differential reflectivity of Si(111)2x1 surface with polarized light: a test for surface structure, “Physical review letters”, 52, 1984, pp. 1145-1147.
Chiarotti 1971: Chiarotti, Gianfranco e altri, Optical absorption of surface states in ultrahigh vacuum cleaved (111) surfaces of Ge and Si, “Physical review”, B4, 1971, pp. 3398-3402.
Feenstra 1986: Feenstra, Randall M. - Thompson, W.A. - Fein, A.P., Real-space observation of pi-bonded chains and surface disorder on Si(111)2x1, “Physical review letters”, 56, 1986, pp. 608-611.
Hamers 1986: Hamers, Robert J. - Tromp, Rudolph M. - Demuth, Joseph E., Surface electronic structure of Si (111)-(7x7) resolved in real space, “Physical review letters”, 56, 1986, pp. 1972-1975.
Jona 1967: Jona, Franco, A note on the sensitivity of LEED to surface perfection, “Surface science”, 8, 1967, pp. 478-484.
Kahng, Atalla 1960: Kahng, Dawon - Atalla, Martin M., Silicon-silicon dioxide field induced surface devices, Memorandum presented at the IRE-AIEE Solid-state Device Research Conference, Pittsburg, Carnegie Institute of Technology, 1960 (rist. in: Semiconductor devices: pioneering papers, edited by Simon M. Sze, Singapore, World Scientific, 1991, pp. 583-596).
Lüth 1995: Lüth, Hans, Surfaces and interfaces of solid mater-ials, 3. ed., Berlin, Springer, 1995.
Mönch 1995: Mönch, Winfried, Semiconductor surfaces and interfaces, 2. ed., Berlin, Springer, 1995.
Pandey 1981: Pandey, K.C., New pi-bonded chain model for Si(111)-(2x1) surface, “Physical review letters”, 47, 1981, pp. 1913-1917.
Schottky 1938: Schottky, Walter, Halbleitertheorie der Sperrschicht, “Naturwissenschaft”, 26, 1938, p. 843.
Shockley 1939: Shockley, William, On the surface states associated with a periodic potential, “Physical review”, 56, 1939, pp. 317-323.
Shockley, Pearson 1948: Shockley, William - Pearson, Gerald L., Modulation of conductance of thin films of semi-conductors by surface charges, “Physical review”, 74, 1948, pp. 232-233.
Shockley 1949: Shockley, William, The theory of p-n junctions in semiconductors and p-n junction transistors, “Bell System technical journal”, 28, 1949, pp. 435-489.
Takayanagi 1985: Takayanagi, Kunio e altri, Structure analysis of Si(111)7x7 reconstructed surface by transmission electron diffraction and microscopy, “Journal of vacuum scienceand technology”, A3, 1985, pp. 1502-1506.
Tamm 1932: Tamm, Igor, Über eine mögliche Art der Elektronenbindung an Kristalloberflächen, "Zeitschrift für Physik”, 76, 1932, pp. 849-850.
Tromp 1983: Tromp, Rudolf M. - Smit, L. - van der Veen, J.F., Si(111)-(2x1) surface: buckling, chains or molecules?, “Physical review letters”, 51, 1983, pp. 1672-1675.
Tavola I
Il MOSFET (Metal oxide semiconductor field effect transistor)
Per spiegare il funzionamento del transistore a effetto campo (MOSFET) conviene partire dalla condizione ideale di assenza di stati di superficie, premettendo qualche nozione sulla struttura a bande dei semiconduttori.
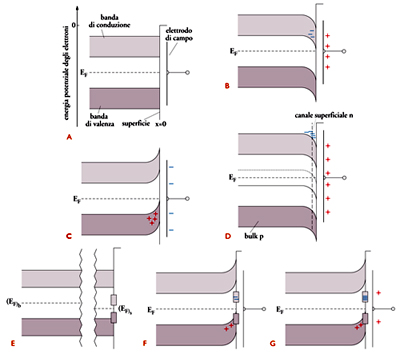
Tale struttura è mostrata nella fig. 1, dove sono riportate le energie potenziali degli elettroni della banda di valenza e di conduzione in funzione di x (x〈0), normale alla superficie. Nello schema è anche indicato il livello di Fermi EF, che nel caso di un semiconduttore intrinseco si posiziona all’incirca a metà della gap proibita, e, sulla destra, l’elettrodo di campo. La fig. 1A si riferisce alla condizione di campo elettrico esterno nullo, ossia con nessuna carica sull’elettrodo di campo. Quando tale elettrodo viene caricato (positivamente o negativamente), come nelle figg. 1B e C, vengono indotte sul semiconduttore cariche di segno opposto. Poiché il semiconduttore è un conduttore imperfetto, le cariche indotte non si collocano sul piano di superficie (come avverrebbe in un metallo) ma occupano una zona di carica spaziale superficiale avente uno spessore dell’ordine di una lunghezza di schermo caratteristica, chiamata lunghezza di Debye (LD). Per mezzo delle equazioni dell’elettrostatica e delle relazioni che legano le densità dei portatori di carica alla posizione del livello di Fermi, è possibile ottenere l’andamento, in funzione di x, delle bande di energia degli elettroni (mostrato schematicamente nelle figure) e calcolare la lunghezza di Debye.
Risulta per LD :
dove kB è la costante di Boltzmann, T la temperatura assoluta, q la carica dell’elettrone, ε0 la costante dielettrica del vuoto e εb quella (relativa) del materiale; nb e pb sono le densità degli elettroni e delle lacune nel bulk. Come si vede dalla formula, LD diminuisce al crescere delle densità dei portatori di carica. Valori tipici di LD nei semiconduttori sono: per il Si intrinseco circa 30 μm e per il Ge intrinseco circa 0,7 μm. Nei metalli LD è inferiore alle distanze interatomiche e perciò perde ogni significato fisico.
Le figg. 1B e C illustrano il funzionamento del dispositivo MOSFET, ossia la variazione della resistenza del semiconduttore in funzione della carica sull’elettrodo di campo. Tale funzionamento (illustrato nelle figure per un semiconduttore intrinseco) rimane tuttavia invariato anche per semiconduttori di tipo n o p. In questi casi però la condizione di superficie intrinseca (livello di Fermi coincidente, approssimativamente, con la metà della gap) si manifesta (anziché con elettrodo di campo neutro) con elettrodo negativo per un semiconduttore n e positivo per un semiconduttore p. Aumentando i valori del potenziale applicato si può anche ottenere una condizione di inversione superficiale: bulk di tipo n e superficie di tipo p (o viceversa). Questa condizione è illustrata nella fig. 1D, che mostra un canale superficiale di tipo n su un campione di tipo p (per maggiore chiarezza nella figura è riportata una linea punteggiata che individua la metà della gap). Questa proprietà viene sfruttata nella tecnologia dei MOSFET e verrà discussa in connessione con la fig. 2.
Si deve qui osservare che la presenza di stati elettronici di superficie altera in modo sostanziale lo schema delle figg. 1B e C, rendendo impossibile il funzionamento del MOS, come osservato nel 1948 da Bardeen. Per illustrare ciò, nella fig. 1E è stata riportata a sinistra la struttura a bande di un semiconduttore intrinseco e a destra quella della sua superficie, come se fossero due fasi separate, con una diversa distribuzione di stati e un diverso livello di Fermi. Per analogia con quanto si osserva realmente, la struttura degli stati di superficie è stata modellizzata con due bande, una piena e una vuota, separate da una gap. Quando la superficie viene adagiata sul semiconduttore, a causa della differenza dei livelli di Fermi, alcuni elettroni del bulk vanno a occupare una parte dei livelli vuoti delle bande di superficie fino a che, all’equilibrio, i livelli di Fermi sono gli stessi per le due fasi. La situazione diventa quella illustrata nella fig. 1F, che mostra la presenza di un incurvamento delle bande anche in assenza di un campo esterno. Si può inoltre verificare che un semiconduttore di tipo n abbia una superficie di tipo p (e viceversa). Questo fatto è stato già menzionato come causa del malfunzionamento di un transistore bipolare.
Un effetto potenzialmente più grave si ha tuttavia nel caso del MOSFET. Se nello schema della fig. 1F carichiamo l’elettrodo di campo, per esempio positivamente (fig. 1G), gli elettroni indotti vanno a collocarsi sui livelli vuoti degli stati di superficie schermando completamente la carica positiva dell’elettrodo di campo. La regione di carica spaziale non sente più un’eventuale variazione della carica sull’elettrodo esterno e conseguentemente non si ha variazione dell’incurvamento delle bande né della resistenza del semiconduttore quando un segnale è applicato all’elettrodo, compromettendo il funzionamento del MOSFET. È pertanto necessario controllare la superficie eliminando, per quanto possibile, gli stati di superficie associati ai legami non saturi (DB) o a altri difetti, mediante il processo di passivazione descritto in precedenza.
In assenza di stati di superficie il comportamento delle strutture a bande ritorna quello illustrato nelle figg. 1B e C.
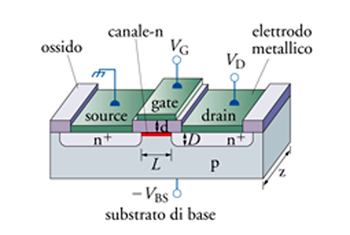
La fig. 2 mostra un dispositivo MOSFET. Il canale superficiale è costituito dallo strato di inversione n (in rosso nella figura) generato da una tensione positiva sull’elettrodo di campo (chiamato porta o gate) come nella fig. 1D. Il segnale da amplificare è applicato tra il gate e il supporto di base (o talvolta tra gate e source). Il segnale amplificato si ottiene dalla variazione della corrente che fluisce tra source e drain. Il MOSFET funziona in entrata come un dispositivo a resistenza infinita (circuito aperto) e in uscita come un generatore di corrente.
Le dimensioni lineari del dispositivo di fig. 2 sono dell’ordine della decina di μm e permettono l’integrazione su un singolo chip di molti milioni di MOSFET.
Tavola II
Si(111)737
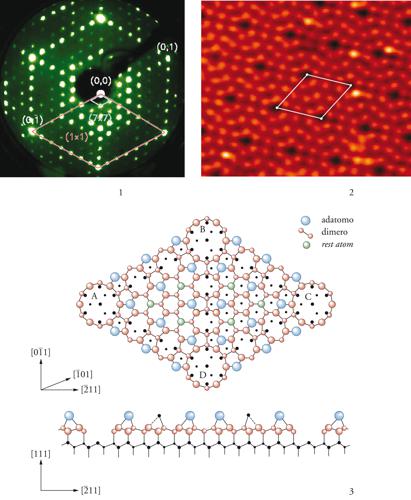
La ricostruzione si ottiene riscaldando una superficie di sfaldatura a temperature maggiori di 250 °C oppure ‘ricuocendo’ una superficie pulita per bombardamento ionico (in generale con argon) o semplicemente per crescita epitassiale. La fig. 1 mostra il diagramma LEED che mette in evidenza come i lati dell’esagono (caratteristico di una superficie ideale) siano divisi in sette parti (Jona 1967). Il modello di ricostruzione di questa superficie è sfuggito per molti anni all’analisi teorica.
La fig. 2 riporta una immagine STM della superficie. Si vede chiaramente: (a) che la cella elementare ha quattro posti vacanti nei vertici dei rombi; (b) che vi sono 616 atomi in posizione più elevata (chiamati adatomi). Osservazioni più precise mostrano che i due triangoli isosceli che dividono il rombo (hanno come base la diagonale più corta) non sono equivalenti. Ciò suggerisce che vi possa essere un difetto di impacchettamento (stacking fault) negli ultimi piani sotto la superficie. Un’indagine molto accurata dell’intensità delle macchie di diffrazione ottenute con elettroni di alta energia (100 keV), in modo da evitare i problemi connessi con la diffusione multipla, ha permesso a Takayanagi e ai suoi collaboratori di proporre il modello della fig. 3 chiamato DAS (Dimers adatoms stacking faults). La figura, che rappresenta una porzione un po’ più grande di una cella elementare (il rombo ABCD, con il posto vacante in ogni vertice) mostra la superficie vista dall’alto e di fianco: sono chiaramente visibili i posti vacanti, i 12 adatomi, i 9 dimeri, una diversa struttura dei piani sottostanti nella parte destra e sinistra, i 313 atomi in posizione normale (rest atom). In totale i legami non saturati (DB) (che sarebbero 737549 nella superficie ideale) diventano 19 (1 nella vacanza, 12 negli adatomi, 6 negli atomi in posizione normale). Il principio della riduzione dei DB è senz’altro verificato anche se non è sufficiente a spiegare una struttura complessa come quella della fig. 3.