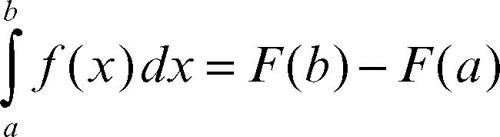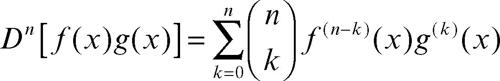Newton-Leibniz, formula di
Newton-Leibniz, formula di
Newton-Leibniz, formula di denominazione attribuita a due diverse formule: la prima, che la tradizione pone alla base di una disputa tra i due matematici, sintetizza il cosiddetto teorema fondamentale del calcolo integrale; la seconda riguarda il calcolo della derivata.
☐ Nel calcolo integrale, la formula esprime il legame tra le nozioni di integrale definito e di integrale indefinito, riducendo in molti casi il calcolo del primo all’individuazione di una primitiva della funzione integranda. Essa, infatti, per una funzione continua F in un intervallo [a, b] esprime la relazione
dove F(x) è una generica primitiva di ƒ(x).
☐ Nel calcolo delle derivate, è spesso così chiamata la formula che fornisce la derivata n-esima del prodotto di due funzioni ƒ(x) e g(x) (altre volte riportata anche come regola di Leibniz):
dove
indica il coefficiente binomiale e si legge «n sopra k».