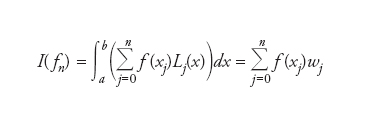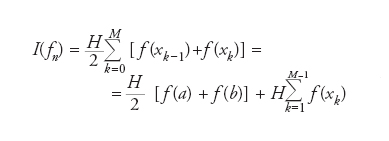formule di Newton-Cotes
formule di Newton-Cotes
Per calcolare numericamente l’integrale definito I(f)=∫∮]] f (x)dx, le formule di Newton-Cotes si ottengono sostituendo la funzione integranda f(x) con un polinomio di Lagrange che interpoli f(x) su un insieme di nodi equispaziati in [a,b]. Se indichiamo con {x}}{[}=0 i nodi di interpolazione e con {L}(x)}{[}=0 i polinomi di Lagrange di grado n definiti sui nodi {x}}, ovvero dei polinomi algebrici di grado n tali che L∥(x})=δ∥} per i,j=0,…,n, l’approssimazione del valore I(f ) con una formula di Newton-Cotes su n+1 nodi sarà data da
dove i valori w}=∫∮]] L}(x)dx sono i cosiddetti pesi della formula di quadratura. Le formule di Newton-Cotes si possono definire di tipo aperto qualora a〈x0〈…〈x{[〈b, e di tipo chiuso qualora a=x0〈…〈x{[=b. Esempi notevoli sono la formula del punto medio – una formula aperta che utilizza un solo nodo – la formula dei trapezi – una formula chiusa che utilizza due nodi – e la formula di Cavalieri-Simpson – una formula chiusa che utilizza tre nodi. Una formula di Newton-Cotes che utilizzi n+1 nodi integra esattamente tutti i polinomi di grado minore o uguale a n se n è dispari, tutti i polinomi di grado n+1 se n è pari. Le formule di Newton-Cotes possono essere utilizzate nella cosiddetta forma composita, qualora l’intervallo di integrazione venga rivisto come l’unione di M sottointervalli disgiunti la cui massima ampiezza è H, e su ogni sottointervallo si usi una formula di quadratura di Newton-Cotes su n+1 nodi. Per es., indicando ancora con I(f{[) l’integrale approssimato, la formula dei trapezi composita si leggerà
Se la funzione integranda è sufficientemente regolare, si può dimostrare che l’errore E{[(f)=I(f)−I(f{[) commesso nel sostituire il modello numerico (ossia le formule di Newton-Cotes composite) al modello matematico converge a zero per H→0 (o equivalentemente per M→∞). In particolare E{[(f) è un infinitesimo di ordine n+1 rispetto ad H se n è dispari, mentre è un infinitesimo di ordine n+2 rispetto ad H se n è pari. Si osserva che qualora si utilizzino più di 8 nodi (n≥7), alcuni pesi delle formule di Newton-Cotes risultano negativi dando luogo a possibili errori di cancellazione e generando quindi instabilità numeriche.