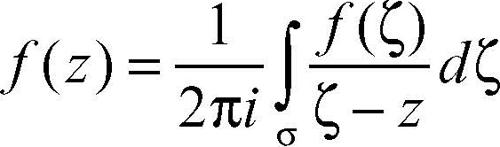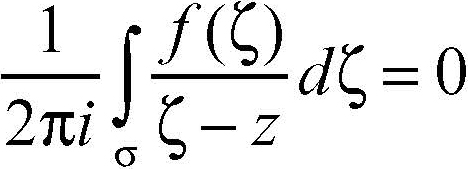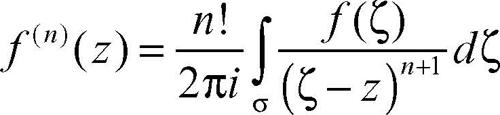Cauchy, formule integrali di

Cauchy, formule integrali di

Cauchy, formule integrali di formule che esprimono il valore di una funzione olomorfa ƒ(z) in ogni punto interno a un dominio del piano complesso mediante i valori assunti sulla frontiera. Siano Ω un dominio del piano complesso avente come frontiera un ciclo σ percorso in verso antiorario, ƒ(z) una funzione olomorfa in Ω e continua in

Allora se z ∈ Ω risulta

mentre se z ∉ Ω risulta

Le due formule valgono anche se il dominio non è semplicemente connesso a patto di percorrere la frontiera nel verso che lascia Ω a sinistra. Dalla prima formula si ottengono per derivazione le formule

che mostrano che ogni funzione analitica è derivabile infinite volte nel suo campo di olomorfia; da esse si ricavano sia lo sviluppo di Taylor di ƒ(z) in un intorno di un punto di regolarità (→ Taylor, serie di) sia lo sviluppo di Laurent relativo a un punto singolare isolato (→ Laurent, serie di).