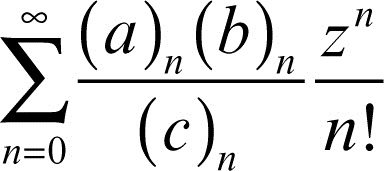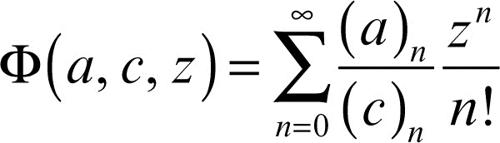funzione ipergeometrica
funzione ipergeometrica
funzione ipergeometrica detta anche funzione ipergeometrica di Gauss e indicata con F(a, b; c; z), è definita nel cerchio |z| < 1 dalla serie ipergeometrica
dove (a)n è il simbolo di → Pochhammer ascendente: (a)n = a(a + 1) ... (a + n − 1). I parametri a e b sono intercambiabili. Per a = 1, b = c, la serie si riduce alla serie geometrica ed è dunque F(1, c; c; z) = 1/(1 − z). Altri casi particolari sono ln(1 − z) = z ⋅ F(1, 1; 2; z), arcsinz = z ⋅ F(1/2, 1/2; 3/2; z 2), arctan(z) = z ⋅ F(1/2, 1; 3/2; −z 2).
La funzione F soddisfa l’equazione differenziale (ipergeometrica)
La derivata della funzione ipergeometrica F(a, b; c; z) è
Facendo il limite per b → ∞ della funzione ipergeometrica F(a, b; c; z/b) si ottiene la funzione ipergeometrica confluente di Kummer
soluzione dell’equazione differenziale (anch’essa detta confluente) zy″ + (c − z)y′ − ay = 0 (si vedano le tavole delle funzioni speciali).
