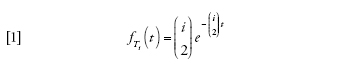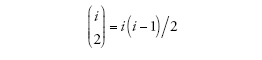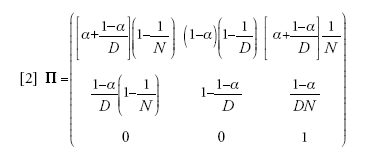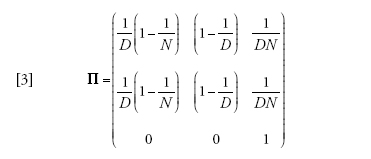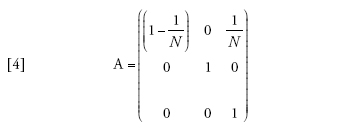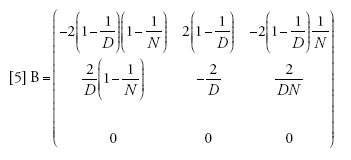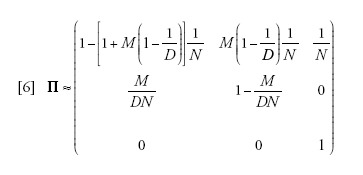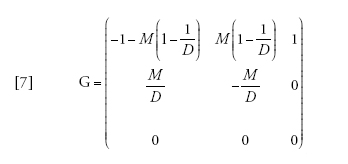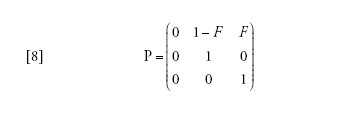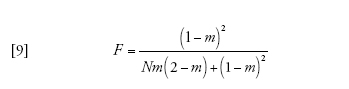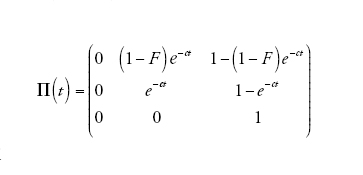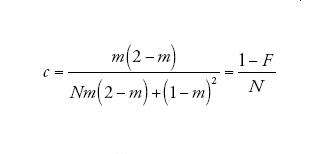Genetica. Modelli matematici per la genetica delle popolazioni
Genetica. Modelli matematici per la genetica delle popolazioni
La teoria della genetica delle popolazioni è stata fin dal principio fondata sui dati. Ronald A. Fisher, in un articolo del 1918 spesso indicato come atto di nascita di questo campo di ricerca, si avvalse della matematica per dimostrare che due insiemi di dati apparentemente in conflitto erano in realtà in perfetta armonia. In particolare, Fisher mostrò che le correlazioni rilevate tra soggetti imparentati, oggetto di studio dei biometristi, potevano essere spiegate dal contributo di un elevato numero di fattori mendeliani (conosciuti come loci polimorfici) ciascuno dei quali dotato di per sé di un effetto modesto sull'organismo e sul suo valore adattativo. Fu proprio in quell'articolo che Fisher introdusse la varianza e la covarianza come le più naturali e le migliori misure di dispersione e di correlazione, mostrando che è molto più facile separare i diversi fattori che contribuiscono alla varianza che non scomporre la deviazione standard, che era la misura favorita dei biometristi. In quell'articolo e nei successivi, Fisher sviluppò il metodo dell'analisi della varianza, che sarebbe diventata una delle pietre miliari dell'analisi statistica.
L'articolo ripercorre la storia di tali progressi e presenta alcuni dei modelli matematici utilizzati. Le analisi effettuate per lo studio della genealogia dei geni in campioni di popolazioni demograficamente complesse, che a volte producono risultati sorprendentemente semplici, sono ben illustrate dal modello dell'isola, elaborato da Sewall Wright nel 1931 per descrivere l'evoluzione delle frequenze geniche all'interno di una popolazione composta da diversi gruppi (detti demi) e isolata dalle altre popolazioni che appartengono alla stessa specie. Per quanto la situazione sia teoricamente semplificata, la validità delle conclusioni ottenute con il modello dell'isola non è limitata né a campioni necessariamente esigui né a strutture di popolazione necessariamente semplici.
I lavori negli anni Trenta di Fisher, Sewall Wright e John B.S. Haldane hanno gettato le fondamenta della teoria della genetica delle popolazioni, ottenendo risultati fondamentali cui si fa riferimento ancora oggi. Approssimativamente dal 1940 alla metà degli anni Sessanta, questi e altri autori produssero anche un gran numero di risultati matematici relativi ai processi evoluzionistici e al mantenimento della variabilità genetica all'interno delle popolazioni. Inoltre, tale periodo vide il campo di ricerca estendersi a un territorio matematico ancor più sofisticato, grazie a figure di spicco quali Gustave Malécot e Motoo Kimura. Pur procedendo senza l'ausilio di dati genetici diretti, questo lavoro preparò il terreno ai progressi fondati su dati che sarebbero stati in seguito resi possibili dall'introduzione della tecnica della gel elettroforesi nella genetica delle popolazioni.
Ancora una volta furono i dati disponibili, in questo caso relativi alla variabilità allozimica entro e tra le popolazioni, a sollecitare lo sviluppo della teoria. Warren J. Ewens (1972) ha proposto una nuova distribuzione statistica, che prediceva per un campione estratto da una popolazione di grandi dimensioni i pattern di variazione allozimica neutrale dal punto di vista della selezione naturale. L'introduzione della formula di campionamento di Ewens segnò l'inizio del passaggio dall'approccio prospettico della genetica delle popolazioni classica a un punto di vista nuovo, retrospettivo, che avrebbe trovato il suo fulcro nel coalescente di Kingman.
La genetica delle popolazioni ha fatto importanti passi avanti negli ultimissimi decenni, soprattutto grazie allo sviluppo delle tecniche di sequenziamento del DNA, con le quali è oggi più semplice raccogliere grandi quantità di dati genetici. I modelli teorici e le tecniche computazionali più appropriate ad analizzarli sono tuttora in corso di elaborazione. La sfida che tanto la metodologia computazionale quanto la teoria analitica per la genetica delle popolazioni si trovano a dover affrontare è quella di sviluppare modelli e tecniche che consentano di estrarre più informazione possibile da set di dati genetici multi-locus, cioè che hanno a che fare con diverse componenti genetiche contemporaneamente. I risultati del Progetto genoma umano e degli attuali programmi di ricerca della variabilità genetica all'interno della specie umana sono alcuni degli spazi disciplinari in cui le analisi matematiche della genetica di popolazioni torneranno più utili. Tramite queste analisi si potrà dare un significato all'enorme mole di dati che questi progetti di ricerca stanno producendo, aiutando a ricostruire la storia filogenetica delle popolazioni umane e interpretare la nostra dimensione genetica alla luce dell'evoluzione.
Il coalescente di Kingman
Warren J. Ewens sviluppò la sua formula di campionamento a partire dalla nozione di 'identità per discendenza' introdotta da Gustave Malécot e facendo proprio l'assunto della 'mutazione ad alleli infiniti' (il modello IAM). Ciò sollecitò una serie di studi che descrivevano l'approssimazione della diffusione (proseguendo dunque il lavoro di Motoo Kimura) per il modello neutrale degli alleli infiniti. Poiché in tale modello gli alleli sono sempre 'imparentati' in senso genealogico, questo lavoro fu determinante per i successivi progressi compiuti dalla genetica delle popolazioni, ovvero per l'introduzione del processo del coalescente. Nell'ambito del modello a siti infiniti, così come di altri modelli appropriati alla descrizione del DNA, il coalescente è particolarmente adatto all'analisi dei dati di sequenza. Non è un caso che la sua introduzione abbia coinciso con la prima applicazione delle tecniche di sequenziamento del DNA al problema della misurazione della variazione genetica.
In breve, se si assume la neutralità selettiva delle mutazioni, è possibile modellare soltanto la storia del campione, senza tenere conto del resto della popolazione. La selezione può essere inserita facilmente se è forte, mentre i modelli del coalescente sono più complessi in caso di selezione debole. Il coalescente, così come viene tipicamente presentato in genetica delle popolazioni, fa propri tutti gli assunti abituali del modello di popolazione di Wright e Fisher. Oltre alla neutralità selettiva, presuppone che la popolazione abbia una grandezza costante e che non sia in alcun modo strutturata (per geografia, genere, età o accoppiamento non casuale). Ciò rende i membri del campione, o le sue linee di discendenza così come vengono ricostruite andando a ritroso nel tempo, intercambiabili in senso statistico, il che significa che non si distinguono per alcuna proprietà che possa influire sui tassi di coalescenza.
Se il tempo viene misurato in unità di Ne=N/σ2 generazioni, in cui N è la grandezza della popolazione e σ2 la varianza del numero di figli tra i membri della popolazione, e se la grandezza effettiva Ne è elevata, allora il tasso di coalescenza è uguale a uno per ciascun paio di linee di discendenza del campione. Inoltre, ciascun evento di coalescenza riguarda soltanto due linee, e dunque la storia del campione di grandezza n andando a ritroso fino al progenitore comune più recente include esattamente n−1 coalescenze. I tempi Ti tra coalescenze sono distribuiti esponenzialmente e dipendono dal numero i di linee di discendenza presenti durante ciascun intervallo:
[1] formula
dove
è il numero dei possibili appaiamenti di i linee. Nel caso specifico di un campione la cui numerosità sia pari a due, il tempo necessario per arrivare al più recente progenitore comune è distribuito esponenzialmente con tasso uguale a uno (ponendo cioè che i=2). L'intercambiabilità delle linee di discendenza comporta che quando si verifica una coalescenza tra i membri di un campione, ogni paio di linee ha le stesse probabilità di ogni altro di esserne protagonista.
Formalmente, l'equazione [1] è valida quando la grandezza del campione è fissata a n in molti modelli di popolazione intercambiabile, se la grandezza della popolazione N tende a infinito e se il tempo è misurato in maniera appropriata (ovvero in unità di Ne=N/σ2 generazioni). Nel limite con N→∞, la possibilità che si verifichino coalescenze multiple in una singola generazione diventa trascurabile, e il processo a tempo discreto proprio della discendenza genetica è sostituito dal processo a tempo continuo rappresentato dall'equazione [1]. Il modello che ne risulta viene utilizzato per l'approssimazione del processo di discendenza genetica nei casi in cui la grandezza del campione sia notevolmente inferiore a quella della popolazione.
Gli ultimi sviluppi della genetica delle popolazioni
Gli anni più recenti hanno visto una notevole diffusione delle tecniche di sequenziamento del DNA e di altre tecniche di genotipizzazione, in seguito ai progetti relativi al genoma umano e di altri organismi. I progressi tecnici, tra i quali l'uso della robotica, sono entrati nella maggior parte delle università e hanno velocizzato la raccolta di set di dati genetici relativamente grandi anche in organismi che non vengono abitualmente impiegati come modelli. In particolare, oggi è facile eseguire analisi multi-locus, mentre venti anni fa era impresa ardua anche ottenere le sequenze di un singolo locus. Ciò è di importanza fondamentale per il campo della genetica delle popolazioni, poiché studiando molteplici loci è possibile scoprire sia pattern riguardanti l'intero genoma sia effetti locus-specifici. La strutturazione della popolazione corrisponde per esempio a un fenomeno che influisce in maniera analoga su tutti i loci del genoma, mentre la selezione naturale è un processo che agisce su singoli loci. Potrebbe essere impossibile separare e comprendere le forze che hanno prodotto e mantenuto la variazione di un singolo locus in mancanza di un quadro più ampio, riferito alla variazione dell'intero genoma, poiché un singolo locus rappresenta soltanto uno degli esiti del processo stocastico e multifattoriale della discendenza intrapopolazione. Attualmente, gli insiemi di dati con il numero di loci più elevato sono quelli relativi all'uomo e a modelli animali come Arabidopsis, Drosophila e il topo.
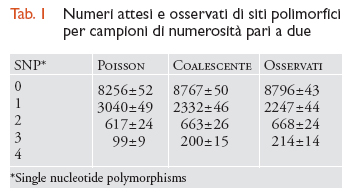
Alcune osservazioni compiute dalla genetica delle popolazioni umane illustrano bene le future sfide e speranze del campo di ricerca. Per esempio, la tab. 1 mostra le predizioni teoriche e i numeri osservati di siti polimorfici per campioni di numerosità pari a due in 11.027 loci umani dislocati nel genoma più o meno a caso. La tabella mostra che una semplice statistica di Poisson, che sarebbe valida se non vi fosse variazione tra loci nei tempi di coalescenza, produce predizioni piuttosto lontane dai dati reali, mentre le predizioni fatte in base al coalescente standard funzionano molto meglio. Neanche queste ultime, tuttavia, risultano adeguate (χ2=23,85; P〈 0,01), e ciò indica che uno o più assunti del modello del coalescente non sono validi per gli esseri umani. Altre analisi condotte su loci multipli giungono alla conclusione che questo tipo di dati non può essere spiegato da modelli semplici.
Sembra dunque che i dati multi-locus umani contengano informazioni relative a processi ‒ come la migrazione, le variazioni di grandezza della popolazione, e/o la selezione naturale ‒ che non sono modellati dal coalescente standard. Ciò non deve sorprendere, se si considera la storia dinamica degli esseri umani, e permette anzi di sperare che sia possibile fare delle inferenze in merito ad alcuni di questi fenomeni più complessi e interessanti. Un altro esempio è rappresentato da un più dettagliato studio (Reich et al., 2002) che ha misurato le correlazioni tra le lunghezze dei rami dell'albero genealogico (o tempi di coalescenza) di coppie di loci separati da diverse distanze lungo il genoma. Ci si attende che le correlazioni tra tali lunghezze diminuiscano con l'aumentare della distanza tra loci a causa della ricombinazione, e la ricerca ha mostrato che le relative predizioni generate in base al coalescente standard con ricombinazione non erano in grado di spiegare le correlazioni a lungo raggio nel genoma umano. Esse possono essere invece spiegate, almeno parzialmente, dalle predizioni derivate da uno dei modelli di strutturazione della popolazione con migrazione di cui parleremo più avanti (il modello multi-deme).
è dai dati multi-locus come quelli riportati in tab. 1 che trae impulso l'attuale ricerca sia sui modelli teorici sia sulle tecniche statistiche. In termini generali, lo scopo è quello di sviluppare modelli che includano tutti i processi rilevanti e metodi inferenziali che possano servirsi di questo tipo di dati per separare tra loro gli effetti di molteplici forze che agiscono simultaneamente.
Un'altra delle finalità principali della ricerca più recente è quella di sviluppare modelli teorici che siano in grado di aiutare a comprendere storie demografiche complesse e di fornire una base ai metodi di inferenza statistica. I modelli genealogici sono stati ampliati fino a includere, oltre alla già menzionata selezione naturale, le variazioni di grandezza della popolazione, la ricombinazione, la migrazione, e a volte diversi di questi fattori contemporaneamente. Uno dei ruoli più importanti del lavoro analitico è quello di identificare i casi in cui la struttura di modelli complessi e multiparametrici è riducibile a qualcosa di più semplice. Quando ciò è possibile, possono derivarne una comprensione decisamente migliore del gioco tra i vari processi che agiscono sui dati e lo sviluppo di tecniche computazionali più efficienti. Risultati di questo tipo si ottengono studiando il comportamento limite di un modello quando uno o più parametri assumono valori molto grandi o molto piccoli. Il problema diventa allora quello di stabilire se uno di questi modelli più semplici sia appropriato a modellare la storia di una particolare specie. Per illustrare le tecniche e fornire un esempio di tali risultati, passiamo a descrivere cinque limiti matematici di uno dei modelli di suddivisione della popolazione con migrazione.
Coalescenza nel modello dell'isola e semplificazioni
Il modello di suddivisione e migrazione della popolazione dell'isola, proposto da Wright nel 1931, è il modello più studiato di strutturazione geografica in genetica delle popolazioni. Nel modello finito, che qui analizzeremo, la popolazione è suddivisa in un numero D di demi, ciascuno di grandezza pari a N individui aploidi, e ciascuno dei quali accoglie una frazione m di migranti a ogni generazione. I risultati cui perverremo sono validi per una popolazione diploide e monoica se a N si sostituisce 2N. Le applicazioni del modello dell'isola sono limitate, perché in realtà esso non contiene geografia esplicita: i migranti possono provenire con uguali probabilità da uno qualsiasi dei demi della popolazione. Tale modello non è dunque in grado di fare una predizione di 'isolamento per distanza', benché lo siano le sue versioni generalizzate. Esso predice che gli individui appartenenti allo stesso deme avranno tra loro maggiori relazioni che non quelli appartenenti a demi diversi, e viola pertanto l'assunto fondamentale del coalescente, secondo il quale le linee di discendenza sono intercambiabili. Nel modello dell'isola, i tassi di coalescenza tendono a essere più elevati entro lo stesso deme che non tra demi diversi.
Benché le approssimazioni che seguono possano essere fatte anche per modelli di suddivisione più generali, il modello dell'isola finito è complesso quanto basta per illustrare le varie semplificazioni che sono state studiate. Consideriamo un campione di numerosità pari a due: campioni più grandi possono essere trattati con gli stessi metodi, ma anche in questo caso una numerosità limitata è già sufficiente per illustrare i risultati. Assumiamo inoltre che le generazioni non si sovrappongano. Al principio di ciascuna generazione, gli individui appartenenti a ciascun deme forniscono un elevato numero di gameti al pool del proprio deme e a quello di un individuo migrante. La riproduzione avviene entro i singoli demi secondo il modello di Wright-Fisher, con la sola differenza che, se una frazione dei gameti deriva dal pool del deme, un'altra frazione, indicata con m, è fornita dall'individuo migrante. I membri del campione, o le sue linee di discendenza, possono trovarsi in uno dei seguenti due stati: (1) nello stesso deme o (2) in demi differenti. L'unica altra possibilità è che (3) si sia verificata una coalescenza tra le linee di discendenza del campione. La discendenza del campione corrisponde a un processo markoviano a tempo discreto con la seguente matrice di transizione per una generazione singola:
[2] formula
dove α=(1−m)2 è la probabilità che nessuna delle due linee sia migrante.
I valori in Π sono le probabilità di spostarsi tra stati o di rimanere nello stesso stato in una singola generazione andando a ritroso. Per esempio, (Π13) è la probabilità di coalescenza (stato 3) in una singola generazione, posto che le due linee di discendenza si trovino attualmente nello stesso deme (stato 1). Essa è uguale alla probabilità che le due linee siano venute dallo stesso deme, o rimanendo nello stesso deme (con probabilità pari ad α) oppure migrando e avendo lo stesso deme di partenza (con probabilità pari a (1−α)/D), e che esse siano derivate dallo stesso genitore all'interno di quel deme (con probabilità pari a 1/N). Una volta entrati nello stato 3, si hanno zero possibilità di spostarsi nell'1 o nel 2 ‒ e si procede andando a ritroso fino alla sua prima occorrenza, che corrisponde al tempo più recente in cui i membri del campione hanno avuto un progenitore comune. L'analisi di questo modello è finalizzata a ottenere la matrice di transizione della generazione-t, Π(t)=Πt. Quindi (Π(t))13 e (Π(t))23 rappresentano la distribuzione del tempo di coalescenza per un campione di numerosità pari a due con provenienza rispettivamente dallo stesso deme e da due demi differenti.
Benché per la matrice Π mostrata più sopra sia possibile ottenere Π(t) abbastanza facilmente, calcolando gli autovalori e gli autovettori della matrice, il risultato (non mostrato) è comunque complesso a fronte della semplicità del coalescente non strutturato. Inoltre, nel caso di grandezza del campione superiore a due la matrice diventa molto grande, e l'algebra si fa ingestibile se tale grandezza si avvicina a cinque. La complessità di molte popolazioni naturali può essere non ulteriormente riducibile, e può in realtà essere notevolmente più complessa di quanto non descriva il modello finito dell'isola. Tuttavia, esistono alcuni casi particolari di tale modello la cui semplicità è paragonabile a quella del coalescente. Molti di essi colgono comunque l'essenza della suddivisione secondo il modello dell'isola, ovvero la più stretta parentela entro lo stesso deme che non tra demi diversi, mentre altri collassano fino a somigliare ai casi non strutturati. Se queste versioni più semplici del modello siano appropriate per una qualche particolare popolazione naturale è una domanda che necessita di una risposta empirica. Alcuni risultati sono ottenibili con relativa facilità, mentre altri hanno bisogno del supporto di un teorema elaborato per i processi markoviani con due scale temporali, del quale parleremo nella sezione dedicata al limite della migrazione bassa.
Il limite della migrazione alta
Un esempio introduttivo, in qualche modo persino banale, è rappresentato dal caso in cui m=1, ovvero in cui gli individui non hanno alcuna tendenza a rimanere fissi in un posto, ad alta migrazione. La matrice di transizione dell'equazione [2] si riduce allora a:
[3] formula.
Naturalmente la popolazione è esattamente panmittica quando m=1, per cui ciascun membro di ciascun deme ha uguali probabilità di provenire da ciascun deme della popolazione. Il processo di riproduzione abbraccia l'intera popolazione, e l'unica traccia di suddivisione è nel fatto che a ogni generazione gli individui risiedono transitoriamente in un deme specifico. Le prime due righe di Π sono dunque identiche; il processo coalescente per un campione dello stesso deme è identico a quello di un campione di deme differenti. Le probabilità delle prime due righe possono essere ottenute immaginando di gettare a caso due palline (linee di discendenza) in D recipienti (demi) ciascuno dei quali contiene N scatole (potenziali genitori).
La matrice dell'equazione [3] specifica che la distanza temporale dal progenitore comune per ciascun paio di linee di discendenza sarà distribuita geometricamente, con la media in generazioni pari alla grandezza totale della popolazione ND. Ciò è identico al risultato che si ottiene nel modello panmittico per n=2. Se si fa l'ulteriore assunto che ND sia grande, e se il tempo viene misurato in unità di ND generazioni, la distribuzione del tempo necessario per arrivare al progenitore comune delle due linee diventa esponenziale come nell'equazione [1].
La migrazione bassa
Il limite della migrazione bassa è stato studiato con un approccio genealogico da Naoyuki Takahata (1991) e Morihiro Notohara (2001), e con uno prospettico da Montgomery Slatkin (1981). Quando il valore di m si avvicina allo zero, la probabilità che nessuna delle due linee migri diviene pari ad α=(1−m)2≈1−2m. La matrice di transizione può essere scritta come la somma Π=A+mB, in cui
[4] formula
e
[5] formula.
Se il tasso di migrazione fosse realmente uguale a zero, allora Π=A, e tra le linee che si trovano in demi differenti non vi sarebbe alcuna possibilità di coalescenza, poiché (A)22=1, mentre le linee dello stesso deme seguirebbero il normale processo di discendenza descritto dal modello di Wright-Fisher e avrebbero una probabilità di coalescenza pari a 1/N a ogni generazione. I valori della seconda riga della matrice B sono importanti, perché rappresentano le probabilità che due linee separate entrino nello stesso deme e abbiano quindi la possibilità di andare incontro a coalescenza. A causa di ciò, la scala temporale del processo coalescente dipenderà da m. Per esempio, il tasso (Π)21=m(B)21 con cui due linee separate entrano nello stesso deme è piccolo se la probabilità di migrazione m è piccola, e dunque il tempo necessario perché ciò accada sarà molto lungo se m è vicina allo zero.
È questa la situazione in cui può essere applicato il teorema di Martin Möhle (1998) per trovare un limite a tempo continuo di un processo a tempo discreto con eventi che si verificano su due scale temporali: veloce nella matrice A e lenta nella matrice mB. Il risultato è quindi considerato un'approssimazione per popolazioni il cui tasso di migrazione sia modesto. Nel limite della migrazione bassa e con il tempo misurato in unità di 1/m generazioni, in un campione di due sequenze dello stesso deme si verificherà immediatamente una coalescenza. In verità, il tempo necessario perché ciò avvenga sarà approssimativamente geometricamente distribuito con una media di N generazioni, ma questa quantità di tempo è trascurabile sulla scala temporale di 1/m generazioni se m→0. Con gli stessi strumenti possono essere studiati gli altri casi limite, come per esempio popolazioni in cui vi è una forte migrazione tra i demi.
Il coalescente strutturato
È il limite che viene tipicamente applicato in genetica delle popolazioni, fin dal lavoro di Wright (1931). è appropriato quando m è piccola e N è grande, per cui gli effetti della migrazione dipendono esclusivamente dal prodotto Nm.
Definendo un nuovo parametro M che sia uguale a 2Nm, e assumendo che N sia grande, la matrice di transizione per una singola generazione diventa:
[6] formula.
Esiste un'approssimazione a tempo continuo in cui il tempo è misurato in unità di N generazioni, che può essere scritta come Π(t)=eGt, in cui
[7] formula
ma tale procedura non è più semplice di quanto sia analizzare direttamente l'equazione [6] o persino la [2]. Tuttavia, per grandezze del campione maggiori di due, il coalescente strutturato è più semplice del modello a tempo discreto, poiché nel primo le coalescenze si verificano singolarmente mentre nel secondo possono verificarsi più coalescenze in una singola generazione.
Il limite multi-deme
Il coalescente strutturato costituisce un modello di suddivisione non banale della popolazione. Ovvero, la distribuzione dei tempi necessari perché si verifichi una coalescenza dipende dalla configurazione del campione, mentre in due degli altri tre limiti ‒ quello della migrazione alta e quello della migrazione forte ‒ il processo genealogico è lo stesso per tutti i tipi di campione. Come il coalescente strutturato, il limite multi-deme per la matrice dell'equazione [2] mostra una struttura di popolazione non banale, ma esso è anche strettamente collegato al coalescente non strutturato. Il limite multi-deme è stato studiato sia con un approccio genealogico sia prospetticamente. Si tratta di un'approssimazione per popolazioni caratterizzate da un elevato numero di demi, e dunque si trova a metà strada tra il modello dell'isola finito e quello infinito.
La semplificazione deriva ancora una volta dall'applicazione del teorema di Möhle, ponendo cheD→∞ nell'equazione [2] e con il tempo misurato inD generazioni. La matrice A contiene i tassi di coalescenza e di migrazione che non portano le due lineedi discendenza nello stesso deme, la matrice B/D riguarda le migrazioni che portano le due linee nellostesso deme. In questo caso,
[8] formula
in cui
[9] formula
corrisponde alla probabilità che due linee che si trovano nello stesso deme vadano incontro a coalescenza prima che vengano separate dalla migrazione. Infine
[10] formula
in cui
[11] formula
descrive il processo di discendenza per un campione di due linee quando il tempo è misurato in D generazioni e D è grande. Dunque, nel limite multi-deme, il tempo necessario per risalire a un progenitore comune per un campione di due sequenze appartenenti a due demi differenti è distribuito esponenzialmente con il tasso c su questa scala temporale. Se il tempo è misurato in unità di ND/(1−F) generazioni, allora il tasso diventa pari a uno proprio come nel caso del coalescente di Kingman. Un campione di due sequenze provenienti dalla stessa popolazione ha inizialmente (al tempo t=0) una probabilità di coalescenza pari a F, e se la probabilità diventa 1−F ha un tempo di coalescenza esponenzialmente distribuito identico a quello di un campione appartenente a un unico deme.
Conclusioni
Tutti i limiti che abbiamo descritto possono essere estesi a campioni più grandi di due. Nel limite della migrazione alta e in quello della migrazione forte, il risultato è sempre il collasso totale che rende il modello simile a quello del coalescente non strutturato. Il coalescente strutturato mantiene la sua complessità, e diventa necessario per modellare la collocazione di tutte le linee andando a ritroso nel tempo. Il limite della bassa migrazione e il limite multi-deme rappresentano due versioni più generali dei processi bifasici che abbiamo descritto. In entrambi i casi, la storia di un campione di sequenze prese singolarmente da demi differenti segue il modello del coalescente non strutturato, ma con una grandezza effettiva diversa dalla dimensione ND della popolazione. Nel limite della bassa migrazione e nel limite multi-deme, questa grandezza effettiva è inversamente proporzionale al tasso di migrazione, poiché la migrazione è il processo che porta due linee nello stesso deme e dà quindi loro la possibilità di andare incontro a coalescenza. Le configurazioni in cui la grandezza del campione è maggiore del numero di demi sono caratterizzate da una storia in due parti. Infatti si verificano inizialmente una gran quantità di coalescenze per i campioni intra-deme, e probabilmente alcuni eventi di migrazione, prima che le linee risultanti, ora tutte in demi separati, entrino in un processo di coalescenza non strutturata. Nel modello multi-deme, queste due fasi sono state chiamate fase di dispersione e di raccoglimento per via del ruolo che in ciascuna di esse ha la migrazione. Nel limite della bassa migrazione, la coalescenza farà convergere tutti i membri di un singolo deme in una singola linea nella fase di dispersione.
Questi limiti possono essere estesi anche a modelli di popolazione più generali, compreso quello della strutturazione in cui i demi differiscono per grandezza e per tasso di migrazione, e in cui la migrazione non è necessariamente altrettanto probabile per ciascun paio di demi. Tuttavia, la complessità del coalescente strutturato aumenta rapidamente, mentre gli altri limiti rimangono funzione di un numero di parametri molto minore poiché sono correlati, per il tramite della grandezza effettiva della popolazione, con il coalescente non strutturato. Per esempio, nel limite della migrazione bassa le storie dipendono soltanto da questa grandezza effettiva, poiché tutte le linee entro-deme vanno incontro a coalescenza nella fase di dispersione. Nel modello multi-deme, la storia del campione dipende direttamente dai parametri dei suoi demi, mentre l'unico effetto dei molti demi non campionati passa per la grandezza effettiva. Diverso è il caso del coalescente strutturato, in cui gli effetti dei demi non campionati non sono catturati in una grandezza effettiva della popolazione, e in cui si assume tipicamente, nelle applicazioni, che i demi campionati costituiscano l'intera popolazione.
Essendo oggi relativamente facile procedere al sequenziamento del DNA, e visti i continui progressi delle biotecnologie, si può prevedere che i set di dati multi-locus rappresenteranno ben presto la norma per gli studi di genetica delle popolazioni, tanto per gli organismi che sono usati come modelli quanto per quelli che non lo sono. I metodi inferenziali e il lavoro analitico sui modelli necessari non soddisfano ancora, tuttavia, le esigenze dei ricercatori, ed è importante che si continui a lavorare in entrambe queste direzioni. I risultati che abbiamo esposto mostrano che scenari demografici complessi possono in alcuni casi essere descritti utilizzando modelli relativamente semplici. Se e quali di questi modelli siano appropriati per una qualche particolare popolazione naturale è una domanda che necessita di una risposta empirica, e che andrebbe presa in considerazione separatamente dalla questione della facilità con cui tali modelli possono essere applicati. Le popolazioni caratterizzate da un numero ridotto di demi, da tassi di migrazione modesti e da una notevole grandezza dei demi hanno bisogno della complessità del coalescente strutturato. Nei casi più semplici, gli effetti strutturali o scompaiono del tutto, come avviene nel caso dei limiti della migrazione alta e di quella forte, oppure si riducono a effetti separabili sulla scala temporale della coalescenza e sui livelli di parentela entro-deme confrontati a quelli tra demi, come nel caso del limite della migrazione bassa e del limite multi-deme. Altri tipi di popolazioni possono comportarsi in maniera diversa, e i metodi che abbiamo esposto possono essere impiegati per derivare i risultati relativi a una varietà di situazioni differenti.
Bibliografia
Beerli 2004: Beerli, Peter, Effect of unsampled populations on the estimation of population sizes and migration rates between sampled populations, "Molecular ecology", 13, 2004, pp. 827-836.
Charlesworth 1998: Charlesworth, Brian, Measures of divergence between populations and the effect of forces that reduce variability, "Molecular biology and evolution", 15, 1998, pp. 538-543.
Ewens 1990: Ewens, Warren J., Population genetics theory - the past and the future, in: Mathematical and statistical developments of evolutionary theory, edited by Sabin Lessard, Amsterdam-Dordrecht-Boston, Kluwer Academic, 1990, pp. 177-227.
Fisher 1918: Fisher, Ronald A., The correlation between relatives on the supposition of Mendelian inheritance, "Philosophical Transactions of the Royal Society of Edinburgh", 52, 1918, pp. 399-433.
Fisher 1930: Fisher, Ronald A., The genetical theory of natural selection, Oxford, Clarendon, 1930.
Haldane 1932: Haldane, John B.S., The causes of evolution, London, Longmans, Green, 1932.
Harpending 1998: Harpending, Henry e altri, Genetic traces of ancient demography, "Proceedings of the National Academy of Sciences USA", 95, 1998, pp. 1961-1967.
Hawks 2000: Hawks, John e altri, Population bottlenecks and Pleistocene human evolution, "Molecular biology and evolution", 17, 2000, pp. 2-22.
Kimura 1955: Kimura, Motoo, Solution of a process of random genetic drift with a continuous model, "Proceedings of the National Academy of Sciences USA", 41, 1955, pp. 144-150.
Kimura 1967: Kimura, Motoo, The number of heterozygous nucleotide sites maintained in a finite population due to the steady flux of mutations, "Genetics", 61, 1967, pp. 893-903.
Kingman 1982a: Kingman, John F.C., The coalescent, "Stochastic processes and their application", 13, 1982, pp. 235-248.
Kingman 1982b: Kingman, John F.C., On the genealogy of large populations, "Journal of applied probability", 19A, 1982, pp. 27-43.
Lewontin 1974: Lewontin, Richard C., The genetic basis of evolutionary change, New York, Columbia University Press, 1974.
Möhle 1998: Möhle, Martin, A convergence theorem for Markov chains arising in population genetics and the coalescent with partial selfing, "Advances in applied probability", 30, 1998, pp. 493-512.
Nordborg 2001: Nordborg, Magnus, Coalescent theory, in: Handbook of statistical genetics, edited by David J. Balding, Martin J. Bishop, Christopher Cannings, Chichester, Wiley, 2001.
Reich 2002: Reich, D. e altri, Human genome sequence variation and the influence of gene history, mutation and recombination, "Nature Genetics", 32, 2002, pp.135-142.
Takahata 1995: Takahata, Naoyuki, A genetic perspective on the origin and history of humans, "Annual review of ecology and systematics", 26, 1995, pp. 343-372.
Wakeley 2003: Wakeley, John, Polymorphism and divergence for island model species, "Genetics", 163, 2003, pp. 411-420.
Watterson 1975: Watterson, G.A., On the number of segregating sites in genetical models without recombination, "Theoretical population biology", 7, 1975, pp. 256-276.
Wright 1931: Wright, Sewall, Evolution in Mendelian populations, "Genetics", 16, 1931, pp. 97-159.
Wright 1943: Wright, Sewall, Isolation by distance, "Genetics", 28, 1943, pp. 114-138.