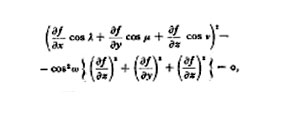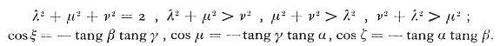DESCRITTIVA, GEOMETRIA
DESCRITTIVA, GEOMETRIA
. Generalità. - 1. È un ramo della geometria che, pur essendosi sviluppato in diretto ricambio di metodi e di vedute con altre teorie geometriche di carattere nettamente speculativo (in particolare con la geometria proiettiva), risponde prevalentemente, nelle sue origini e nei suoi risultati, a esigenze di ordine artistico e tecnico. Sempre si è fatto uso del disegno per rappresentare oggetti a tre dimensioni e per farne rilevare sia l'aspetto d'insieme, sia le varie particolarità di forma e d'estensione. Soprattutto dell'aspetto d'insieme si preoccupa l'artista (prospettiva). L'ingegnere invece, che progetta un'opera qualsiasi, ricorre al disegno sia, in un primo tempo, per studiare la disposizione e la forma delle varie parti dell'opera ideata e per prestabilirne le dimensioni, sia più tardi per fornire ai costruttori tutti i dati necessarî per l'effettiva esecuzione del lavoro. Ora la geometria descrittiva si propone appunto il problema generale di rappresentare graficamente le figure spaziali su di un quadro o foglio del disegno (schematizzato da un piano) in modo che si passi senza ambiguità dalla figura obiettiva alla sua rappresentazione, e viceversa, e di più sia possibile rilevare da questa rappresentazione piana, tutti i caratteri di forma e di grandezza della figura obiettiva.
Così la descrittiva trova applicazione non solo nella prospettiva, ma anche nella teoria delle ombre, nella costruzione delle carte topografiche, nella fotogrammetria, nella stereotomia (o teoria del taglio delle pietre, dei legnami, dei metalli da costruzione) e, per quanto ciò abbia ormai soltanto un interesse storico, nella gnomonica (o teoria della costruzione delle meridiane).
"Metodo di rappresentazione" si dice in geometria descrittiva ogni sistema di procedimenti costruttivi e di convenzioni, che fornisca una soluzione del problema generale dianzi accennato. Si comprende a priori come sia possibile ideare svariati metodi di rappresentazione; ma l'esperienza ha messo in luce per taluni di essi (sia pure in diversa misura e sotto aspetti diversi) particolari pregi di semplicità e di adattabilità ai varî ordini di problemi concreti. E noi qui, senza entrare in sviluppi sistematici, per i quali rimandiamo ai trattati speciali, daremo un cenno dei metodi d'uso più corrente, cominciando da quello del Monge, che in qualche modo estende ad ogni figura la rappresentazione, a tutti famigliare, di un edificio per mezzo della "pianta" e dell'"alzato".
2. Premettiamo che l'operazione fondamentale della geometria descrittiva è, come per la geometria proiettiva, la proiezione, cioè l'operazione per cui, prefissati un punto O (centro di proiezione o di vista) e un piano π (quadro) non passante per O, si associa a ogni punto P dello spazio il punto P′ (proiezione o immagine di P), in cui il quadro è segato dalla semiretta (o raggio proiettante) OP.
Questa proiezione, nell'ipotesi che il centro O sia a distanza finita, si dice centrale, per contrapposto a quella parallela, che si ha quando il centro di vista va a distanza infinita. In particolare la proiezione si dice ortogonale, se il centro è all'infinito nella direzione perpendicolare al quadro.
È manifesto che per individuare una figura dello spazio non basta darne l'immagine, che si ottiene proiettandola su di un dato quadro (da un dato centro). Occorre aggiungere qualche altro dato, e a ciò provvedono, in varî modi, gli svariati metodi di rappresentazione.
Metodo del Monge o della doppia proiezione ortogonale. - 3. Sian dati due piani π1 e π2 fra loro ortogonali (piani di proiezione; fig. 1); nella pratica si suppone in generale il primo parallelo all'orizzonte, donde la ragione degli epiteti orizzontale e verticale con cui vengono distinti di consueto, mentre la loro intersezione t12 porta il nome di linea di terra. Questa divide ciascuno dei piani dati in due regioni, che chiameremo una positiva (π1+, π2+), negativa (π1-, π2-) l'altra. Gli stessi piani dividono tutto lo spazio in quattro regioni che diremo I, II, III, IV, convenendo che la I sia compresa fra π1+ e π2+, la II fra π2+ e π1-, la III fra π1- e π2-, la IV fra π2- e π1+. I quattro diedri formati dagli stessi piani ammettono due piani bisettori, uno (detto primo) che attraversa le regioni I e III, l'altro (detto secondo) che attraversa le regioni II e IV. Per operare sopra un unico piano di disegno s'immagina di ribaltare (cioè far rotare) il piano π2 di 90° attorno alla linea di terra, per modo che π2+ venga a sovrapporsi a π1- (ovvero il piano π1, per modo che π1+ venga a sovrapporsi a π2-).
4. Un punto qualsiasi P dello spazio ha una proiezione ortogonale sopra ciascuno dei piani π1 e π2. Queste due proiezioni P′ e P″, dopo la sovrapposizione dei piani di riferimento, vengono a trovarsi sulla medesima perpendicolare alla linea della terra (ordinata o retta di richiamo). Si deduce facilmente da ciò che esiste una corrispondenza biunivoca fra i punti dello spazio e le coppie di punti del piano del disegno appartenenti alla stessa ordinata; esprimeremo ciò scrivendo P ⊄ (P′, P″), col sottinteso che P′ e P″ si trovino sulla stessa perpendicolare alla linea di terra.
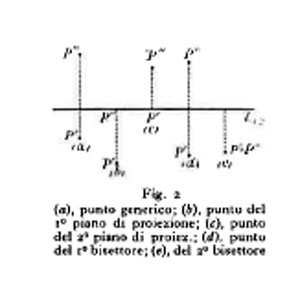
Se P si trova sul piano orizzontale (o verticale) di proiezione, P′ (o P″) coincide con P, mentre P″ (o P′) cade sulla linea di terra; se esso si trova sul primo piano bisettore, le sue proiezioni sono simmetriche rispetto alla linea di terra, mentre se cade sul secondo esse coincidono (fig. 2). Le distanze di un punto P dai piani di proiezione si dicono quote del punto; si conviene che la quota orizzontale sia positiva per i punti delle regioni I e IV, negativa per le altre; che invece la quota verticale sia positiva per i punti delle regioni I e II, negativa per quelli delle regioni III e IV.
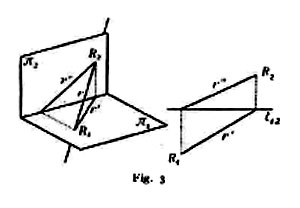
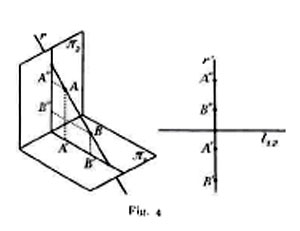
5. Considerazioni analoghe alle precedenti mostrano che qualsiasi retta r dello spazio si può rappresentare, in generale senza ambiguità, mediante le sue due proiezioni r′ e r″ (fig. 3) il che si esprime scrivendo r ⊄ {r′, r″}; fanno eccezione le perpendicolari alla linea di terra o rette di profilo (fig. 4), per individuare le quali è necessario siano dati due punti A, B (con le quattro proiezioni sulla stessa ordinata).
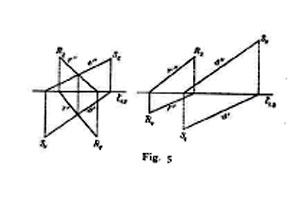
Sopra una retta qualsiasi si sogliono considerare quattro punti notevoli, cioè le intersezioni con i piani di proiezione (tracce, orizzontale R1 e verticale R2 della retta) e quelle con i piani bisettori. Una retta si può determinare, anziché con le sue proiezioni, con le sue tracce; dalla costruzione delle proiezioni, date le tracce, si desume che ogni retta attraversa tre delle quattro regioni dello spazio e si può determinare la regione esclusa. Due rette r ⊄ {r′, r″}e s ⊄ {s′, s″} s'incontrano se i punti r′r″ e s′s″ si trovano sulla stessa ordinata; sono parallele se sono parallele le loro proiezioni (fig. 5).
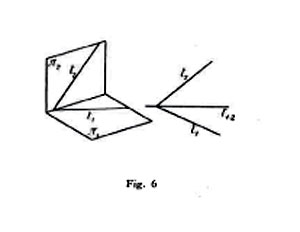
6. Un piano qualsiasi τ si rappresenta per mezzo delle sue intersezioni con i piani di proiezione (tracce del piano); esse si tagliano sopra la linea di terra; scrivendo τ ⊄ [t1, t2] si esprime che il piano τ è quello di tracce t1 e t2, sempre nella supposizione che queste rette s'incontrino sopra la linea di terra (fig. 6).
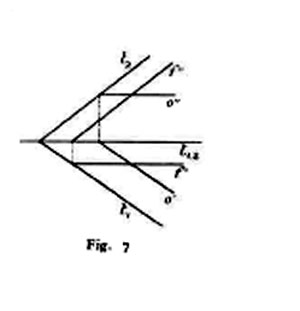
Utile torna anche la considerazione delle intersezioni di un piano arbitrario con i piani paralleli ai piani di proiezione; si chiamano rette principali e precisamente orizzontali quelle parallele a π1, verticali o di fronte quelle parallele a π2 (fig. 7).
Fra le proiezioni orizzontale e verticale di una figura piana qualsiasi sussiste una relazione di affinità, avente per asse la retta in cui coincidono le due proiezioni dell'intersezione del dato piano col secondo piano bisettore; giova in molti casi determinare un piano mediante il suo asse d'affinità e un suo punto, in altri mediante due rette incidenti.
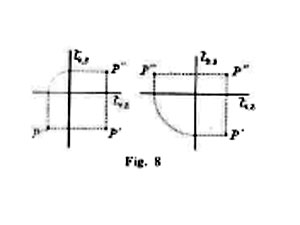
7. Spesso giova ricorrere a un terzo piano di proiezione (piano di profilo) perpendicolare ai precedenti; allora di ogni punto (fig. 8) o retta si deve considerare una terza proiezione e di ogni piano una terza traccia, le quali sono determinate e costruibili servendosi delle prime. I tre piani di proiezione costituiscono un triedro trirettangolo, che può assumersi come triedro di piani coordinati di un sistema cartesiano (v. coordinate); se di un punto si conoscono le proiezioni, si possono trovarne le coordinate, e viceversa; onde ogni problema relativo a rette e piani può risolversi tanto graficamente quanto col calcolo.
8. Queste nozioni sono sufficienti a trattare tutti i problemi di posizione; ogni problema di tal fatta può poi risolversi quando si sappiano sciogliere i quattro fondamentali di cui ecco gli enunciati:
I. Dati due punti, trovarne la congiunzione II. Dati due piani trovarne l’intersezione. III. Trovare il punto comune a una retta e un piano. IV. Trovare il piano che passa per un punto e una retta.
Citiamo altre questioni della stessa specie che si possono risolvere applicando i problemi fondamentali:
I. Determinare il piano che passa per tre punti. II. Determinare il punto comune a tre piani. III. Per un punto condurre una retta che si appoggi a due rette sghembe. IV. In un piano trovare la retta che si appoggia a due rette sghembe.
9. Fra i problemi elementari metrici vanno anzitutto considerati quelli relativi a rette e piani fra loro perpendicolari, cioè: Per un punto condurre il piano perpendicolare a una data retta, oppure la retta perpendicolare a un dato piano o a una data retta; per una retta condurre il piano perpendicolare a un dato piano; costruire la retta che incontra ad angolo retto due date rette sghembe. Essi si risolvono, appoggiandosi ai due seguenti teoremi:
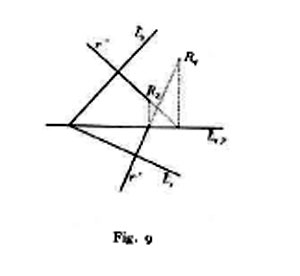
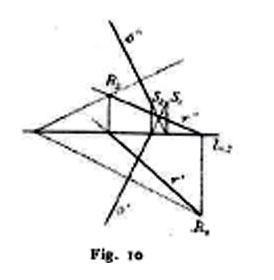
I. Affinché una retta e un piano siano fra loro perpendicolari è, in generale, necessario e sufficiente che le due proiezioni della retta siano perpendicolari alle tracce omonime del piano (fig. 9); nel caso in cui la retta sia perpendicolare alla linea di terra, il piano sarà parallelo alla stessa, onde le sue tracce saranno a essa parallele; deve inoltre la terza proiezione della retta riuscire perpendicolare alla terza traccia del piano. II. Affinché siano fra loro perpendicolari le rette r ⊄ {r′, r″} e s ⊄ {s′, s″} di tracce rispettivamente R1 e R2, S1 e S2, devono tagliarsi sulla linea di terra (fig. 10) le perpendicolari calate da R1 e R2 rispettivamente sopra s′ e s″ (oppure da S1 e S2 rispettivamente sopra r′ e r″).
Fra i problemi metrici in cui i dati o le incognite sono lunghezze o angoli, i più semplici sono: Trovare la distanza fra due punti; trovare gli angoli che formano fra loro due rette; trovare gli angoli che formano fra loro due piani; trovare la minima distanza fra due rette sghembe. Quando siano stati risoluti, si può trovare la distanza fra un punto e una retta o un piano, la distanza di due rette parallele o di due piani fra loro paralleli, l'angolo di una retta con un piano, l'area di un triangolo (anzi di un poligono qualsivoglia) e il volume di un tetraedro (anzi di un poliedro qualsiasi). Questi problemi si possono risolvere o mediante considerazioni dirette, o alterando la posizione scambievole dei dati rispetto agli elementi di riferimento: questo risultato può ottenersi o tenendo fissi i piani di proiezione, o sostituendoli con nuovi piani; questi due espedienti vanno considerati separatamente.
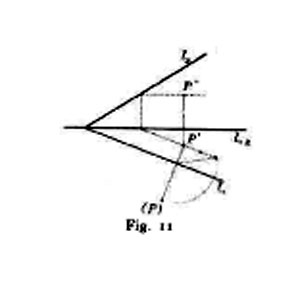
a) Una figura qualsiasi dello spazio si può trasportare da una posizione a un'altra mediante una traslazione accompagnata da una rotazione attorno a un asse, onde è lecito limitarsi a considerare queste due specie di movimenti (v. cinematica, n. 28). Le costruzioni delle rappresentazioni delle nuove posizioni assunte da un punto, da una retta o da un piano per effetto di una traslazione soddisfano alla condizione di semplicità a cui non può sottrarsi qualunque costruzione di geometria descrittiva; ma, affinché altrettanto possa dirsi riguardo a una rotazione, è necessario che l'asse relativo sia perpendicolare a uno dei piani di proiezione. All'anzidetta condizione soddisfano i "ribaltamenti" di un piano obiettivo sopra uno dei piani di proiezione: ragione per cui è questo uno degli artifici più di frequente usati di fronte alle questioni di cui parliamo; riguardo a esso sussiste il seguente importante teorema: se un piano che non sia perpendicolare al primo (o secondo) piano di proiezione si ribalta sopra questo piano intorno alla corrispondente traccia, fra il ribaltamento e la proiezione orizzontale (o verticale) di una figura qualsiasi situata nel piano considerato sussiste un'omologia affine, avente per asse la traccia orizzontale (o verticale) del piano considerato, per centro il punto all'infinito in direzione perpendicolare a questa traccia e finalmente per rapporto d'affinità il coseno di uno degli angoli formati dal piano dato con quello su cui si fa il ribaltamento (fig. 11).
b) Per cambiare i due piani di proiezione si può mutarne uno per volta; limitandosi p. es. a cambiare il piano verticale (per il che basta cambiare la linea di terra), restano immutate le proiezioni e le quote orizzontali di tutti i punti, circostanze che permettono di trovare le nuove proiezioni verticali degli stessi.
Più difficili sono i problemi metrici "inversi", quelli cioè in cui si tratta di determinare un punto, una retta o un piano in base a condizioni in cui entrano angoli o distanze; per risolverli è necessario rícorrere a espedienti variabili da caso a caso.
Va notato che il metodo del Monge, di cui qui si sono accennati i principî, dà, come immagini di rette parallele, rette parallele tanto in prima quanto in seconda proiezione, cosicché non altera notevolmente l'aspetto generale di una figura: di qui il grande e ben giustificato favore di cui esso gode presso i disegnatori e i tecnici in generale.
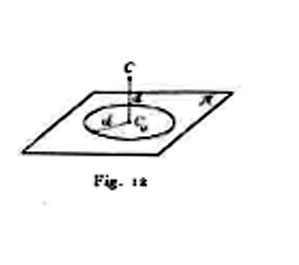
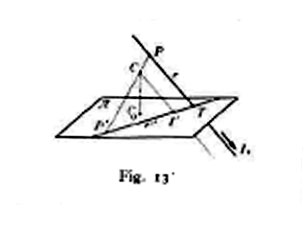
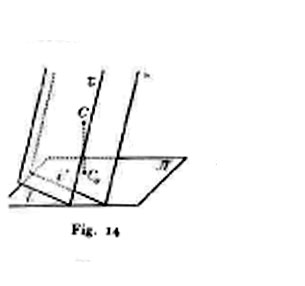
Metodo della proiezione centrale. - 10. Oltre il quadro π sia fissato (fig. 12) un punto proprio C come centro di proiezione, il quale soddisfi all'unica condizione di non appartenere al quadro; per determinarne la posizione supporremo conosciuto il piede C0 della perpendicolare calata da esso sul quadro (punto principale), nonché la lunghezza d della perpendicolare CC0. Invece di dare in disparte la distanza d, si suole descrivere il circolo di centro C0 e raggio d (circolo di distanza). Ogni punto dello spazio ha una determinata proiezione P′ da C su π; P′ è in generale un punto proprio; fanno eccezione esclusivamente i punti del piano π* (detto parallelo anteriore) condotto da C parallelamente a π; similmente qualsiasi retta propria r ha per proiezione una determinata retta r′, la quale si trova all'infinito soltanto quando r giace in π*. Ogni punto di r ha per proiezione un punto di r′; in particolare il punto T = rπ (traccia) di r ha per proiezione sé stesso, mentre il punto all'infinito I∞ della stessa retta ha per proiezione un punto I′ detto punto di fuga della retta (fig. 13). Data r, sono determinati T e I′ e viceversa; ne consegue che per individuare una retta r si possono assumere i punti T e I′, il che si esprime scrivendo r ⊄ {T, I′}; T e I′ coincidono se r passa per il centro di proiezione. Rette parallele fra loro e non al quadro hanno lo stesso punto di fuga; rette incidenti non parallele al quadro sono caratterizzate dall'essere la congiungente delle loro tracce parallela alla congiungente dei loro punti di fuga. Similmente su un piano τ non parallelo al quadro si sogliono considerare l'intersezione t col quadro (traccia) e la retta all'infinito i∞ la cui proiezione i′ si chiama retta di fuga del piano (fig. 14); t e i′ sono fra loro parallele e si assumono come determinatrici del piano, il che si esprime scrivendo τ ⊄ [t, i′]. Finalmente un punto P si suole individuare dandone la proiezione e una retta o un piano su cui giace, e si esprime ciò scrivendo P ⊄ (T, I; P′) o P ⊄ (t, i′; P′) nell'ipotesi che T, I′, P′ siano tre punti in linea retta o che t e i′ siano rette fra loro parallele. Rette e piani paralleli al quadro e punti e rette del piano π esigono metodi speciali di rappresentazione.
Quota di un punto è la sua distanza dal quadro, presa col segno + o − secondoché il punto si trovi o no rispetto al quadro dalla stessa parte del centro. Data la rappresentazione del punto P = (T, P′; I′) la sua quota p può calcolarsi mediante la formula p = d P′T/P′I′.
11. Le precedenti considerazioni bastano per la risoluzione di tutti i problemi di posizione, riguardo ai quali valgono integralmente le osservazioni esposte nel n. 8.
12. I problemi, in cui intervengono condizioni di perpendicolarità rispetto al quadro, si risolvono applicando l'osservazione seguente: condizione necessaria e sufficiente affinché una retta (o un piano) sia perpendicolare al quadro, è che il suo punto di fuga (o la sua retta di fuga) coincida col punto principale (o passi per esso).
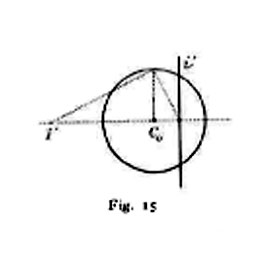
Invece, per risolvere le questioni in cui si presentano condizioni di perpendicolarità fra rette e piani, si ricorre a una speciale correlazione piana involutoria, esente da elementi uniti, che si chiama antipolarità, rispetto al circolo di distanza, per ricordare che è il prodotto (operatorio) della polarità rispetto a codesto circolo per la simmetria rispetto al punto principale; la relazione che intercede fra un punto I′ e la sua antipolare i′ è graficamente espressa dalla fig. 15. Affinché una retta e un piano siano fra loro perpendicolari occorre e basta che la retta di fuga del piano sia antipolare del punto di fuga della retta rispetto al circolo di distanza; sono perpendicolari fra loro due rette i cui punti di fuga siano antireciproci rispetto allo stesso.
13. Per trattare i problemi in cui intervengono distanze di punti e ampiezze di angoli, basta applicare quanto si espose nel n. 9. Gli artifici più utili consistono (anagolamente a quanto avviene nel metodo di Monge) in "ribaltamenti" dei piani obiettivi e nel "mutamento del centro di proiezione".
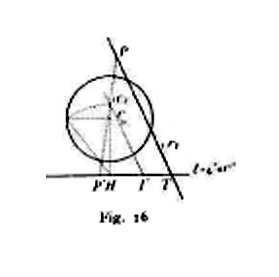
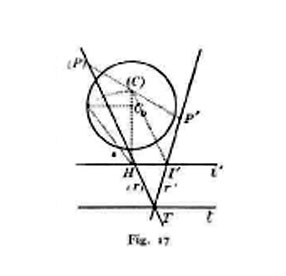
a) Riguardo ai ribaltamenti, giova distinguere il caso in cui si tratti di un piano proiettante dall'ipotesi generale. Nel primo caso (cfr. fig. 16) si comincia a trovare la posizione (C) assunta in conseguenza dal centro di proiezione; allora è facile trovare quella che viene a occupare una retta qualunque {T, I′} e quindi quella di un punto arbitrario P di detta retta, servendosi dell'osservazione che proiezione P′ e ribaltamento (P) di un punto P sono allineati col ribaltamento (C) del centro. Quando invece si ribalta un piano [t, i′] non passante per il centro di proiezione né parallelo al quadro, fra proiezione centrale e ribaltamento di una stessa figura sussiste un'omologia, avente per asse la traccia del dato piano, per centro la posizione che assume il punto C quando si ribalta sul quadro il piano proiettante parallelo al dato, e per una delle rette limiti la retta i′ (fig. 17). Quando finalmente il piano dato sia parallelo al quadro, l'operazione di ribaltamento non differisce da una proiezione ortogonale sul quadro.
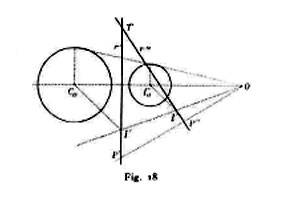
b) Per effettuare il cambiamento del centro è indispensabile conoscere l'antico e il nuovo circolo di distanza e di più sapere se i due centri di proiezione giacciono dalla stessa parte o da parti opposte del quadro; sia O uno dei centri di similitudine di quei circoli e precisamente l'esterno nella prima di queste ipotesi, l'interno nella seconda. Le tracce dei piani e delle rette non mutano per effetto del supposto cambiamento; mentre due elementi di fuga della stessa retta o dello stesso piano si corrispondono nell'omotetia di centro O, diretta nel primo degli anzidetti casi, inversa nell'altro, e in cui il rapporto di omotetia è eguale al rapporto dei raggi delle due distanze; l'antica e la nuova proiezione di un punto, quantunque non si corrispondano in questa omotetia, sono allineati col punto O (fig. 18). Ciò è sufficiente per costruire la nuova rappresentazione di qualsiasi figura. Cambiando il centro di proiezione si può trasformare un piano arbitrario in un piano proiettante.
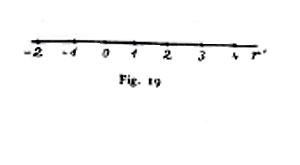
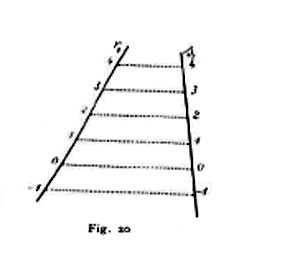
Metodo dei piani quotati. - 14. Si indichi sempre con π il quadro (detto ora piano di paragone) e si chiami positiva una, negativa l'altra delle due regioni in cui esso divide lo spazio. Un punto arbitrario P si potrà individuare mediante la sua proiezione P′ sul quadro π e la sua distanza p (quota) da esso, presa positivamente o negativamente a seconda delle regioni dello spazio in cui si trova P: si esprime ciò scrivendo P ⊄ (P′, p). Una retta r potrà in conseguenza individuarsi assegnando le proiezioni quotate di due suoi punti; e siccome tutti i punti di quota intera di una retta hanno proiezioni che si susseguono a distanze fra loro eguali, così è costume di rappresentare una retta mediante la sua proiezione ortogonale sul quadro, sulla quale sono segnati dei punti equidistanti (fig. 19); è la scala di pendenza della retta, mentre ne è l'intervallo la distanza fra due punti consecutivi della scala. Due rette si tagliano quando le congiungenti le coppie di punti di ugual quota delle loro scale di pendenza costituiscono un fascio di rette parallele (fig. 20). Finalmente un piano si determina dandone una retta di massima (o minima) pendenza; per non confondere le scale di pendenza dei piani con le scale di pendenza delle rette, si segnano le prime nel modo indicato dalla fig. 21. Questo metodo di rappresentazione è usato di preferenza in topografia.
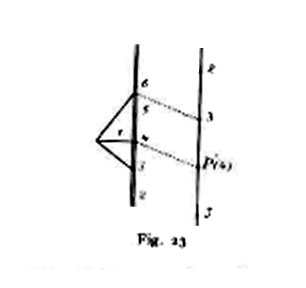
15. Volendolo applicare a risolvere i problemi di geometria di posizione, conviene attenersi alla riduzione ai problemi fondamentali utilizzata nei due metodi precedenti; gli artifici di soluzione sono ancora gli stessi, ma le costruzioni risultano in generale più semplici. Quanto ai problemi in cui si presentano condizioni di ortogonalità, essi si risolvono servendosi del seguente teorema: Affinché una retta e un piano siano fra loro perpendicolari, occorre e basta che le loro scale di pendenza siano fra loro parallele, i loro sensi opposti e i loro intervalli i, i′ inversi l'uno dell'altro (fig. 22). Applicandolo, nulla di più agevole del condurre per un dato punto la retta perpendicolare a un dato piano (fig. 23) o il piano perpendicolare a una data retta.
Alla soluzione dei problemi metrici si possono ancora vantaggiosamente applicare i ribaltamenti, dopo aver osservato che sussiste quell'affinità fra proiezione ortogonale e ribaltamento di una figura qualsiasi, di cui si è parlato trattando del metodo di Monge (n. 9).
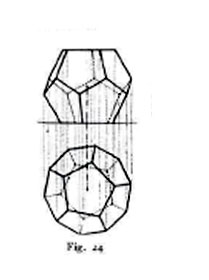
Rappresentazione delle principali figure geometriche. - 16. I metodi esposti (lo stesso si dica degli altri congeneri, di uso meno frequente e che quindi per brevità si tacciono) permettono di rappresentare non soltanto i punti, le rette e i piani, bensì anche ogni altra figura spaziale. Per quanto concerne la rappresentazione dei poliedri, essa si ottiene rappresentandone i singoli vertici e i singoli spigoli; però nell'intento di renderla più espressiva, si suppone che la figura rappresentata appartenga a un corpo materiale e si distinguono le sue facce che sono visibili da quelle che non lo sono rispetto al centro di proiezione e si segnano a tratto continuo i soli spigoli visibili (cfr. per es., la fig. 24). Quando si usa il metodo Monge, la ricerca della visibilità deve essere fatta per ciascuna delle due proiezioni; essa è agevole se si tratta di un poliedro facilmente concepibile, ma in ogni caso può effettuarsi con norme semplici e sicure (G. Loria, Complementi di geometria descrittiva, Milano 1924, pagine 1-29). Ottenuta la rappresentazione di un poliedro, si potrà, applicando uno qualsiasi dei metodi esposti, determinarne l'intersezione con un piano o una retta, nonché costruire l'intersezione di due siffatte figure.
17. Uscendo dallo stretto campo elementare, accenneremo a qualche norma per la rappresentazione delle curve, piane e sghembe, e delle superficie.
Curve piane. - Chi usa il metodo del Monge, per individuare una curva piana si servirà del piano della curva e di una proiezione della stessa; da ciò si può dedurre l'altra proiezione e costruire le tangenti di essa. Similmente se si preferisce altro metodo di rappresentazione. Col mezzo di tali dati si potranno determinare i punti della curva che stanno in un dato piano, le sue tangenti che incontrano una data retta, ecc.
Curve sghembe. - Se si proietta una curva qualunque Γ da un centro C sopra un piano π si ottiene una curva Γ′, la quale ha per punti multipli le proiezioni degli eventuali punti multipli della data e ha inoltre per punti doppî le tracce sul quadro delle corde di Γ che passano per C, e per flessi le proiezioni dei punti di Γ i cui corrispondenti piani osculatori passano per il centro di proiezione; si presentano cuspidi sopra Γ′ se C si trova sopra qualche tangente di Γ.
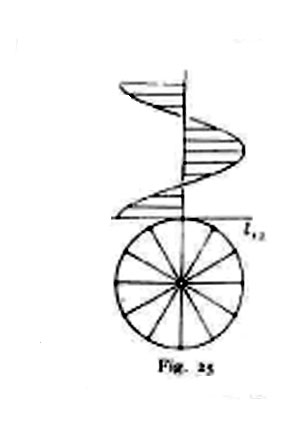
Quando si adopera il metodo del Monge, una curva sghemba Γ si determina dandone le proiezioni Γ′ e Γ″, fra cui sia stabilita una corrispondenza univoca tale che due punti corrispondenti si trovino sulla stessa ordinata (cfr. p. es. la fig. 25, che rappresenta un'elica cilindrica); i punti uniti dànno le intersezioni di Γ col secondo piano bisettore. Allora della curva si potranno determinare le tangenti e i piani osculatori. Similmente se si usa un altro dei noti metodi di rappresentazione.
Superficie. - Quando si proietta una superficie Σ da un punto C sopra un piano π è utile considerare il corrispondente "contorno apparente" K, che è il luogo dei punti di contatto delle rette o dei piani tangenti di Σ passanti per C; la proiezione K′ di K gode la proprietà di riuscire tangente alla proiezione di qualsiasi curva appartenente alla superficie.
Ordinariamente una superficie si suppone generata dal movimento di una curva variabile di forma, grandezza e situazione e suscettibile di una serie semplicemente infinita di posizioni; allora per rappresentare la superficie con uno dei metodi della geometria descrittiva si suole rappresentarne le singole generatrici; talvolta accade di conoscere due generazioni di una stessa superficie e allora, per maggiore chiarezza, si rappresentano entrambi i corrispondenti sistemi di generatrici.
Quando si usa il metodo dei piani quotati, si adottano, come curve generatrici della superficie, le sue sezioni con un sistema di piani paralleli al piano di paragone e fra loro equidistanti (fissando, caso per caso, in modo opportuno l'equidistanza): sono le cosiddette "linee di livello" ben note a chiunque abbia avuto fra mano qualche carta topografica dello Stato maggiore dell'esercito o del Touring Club italiano (cfr. fig. 26).
In un suo punto ordinario P una superficie ammette un piano tangente, il quale si ottiene costruendo le tangenti in P a due curve della superficie passanti per tale punto. La sezione prodotta nella superficie da un piano arbitrario è il luogo geometrico delle intersezioni di questo piano con le ∞1 generatrici della superficie stessa; risolto questo problema, si è in grado di determinare le intersezioni della superficie con una retta arbitraria; ma in certi casi riesce più comodo risolvere questo problema direttamente. Per costruire il contorno apparente di una superficie da un punto O basta determinare i punti di contatto delle tangenti condotte da O a una qualunque delle sezioni prodotte nella superficie da piani passanti per O. Finalmente la linea d'intersezione di due superficie Σ1 e Σ2 si costruisce per punti, segando questa mediante una serie di superficie Σ (spesso, ma non sempre, piane), cioè determinando le curve ΣΣ1, ΣΣ2 e poi i punti comuni a queste; p. es. volendo determinare l'intersezione di due superficie di rotazione ad assi concorrenti in un punto O, giova assumere come ausiliarie le superficie sferiche di centro O (metodo di Monge).
Ombre e chiaroscuro. - 18. L'intento che si prefigge la teoria delle ombre e del chiaroscuro è del genere di quello che consigliò a distinguere le parti visibili dalle invisibili in un poliedro qualsiasi: quello, cioè, di far sì che la rappresentazione produca sull'osservatore un'impressione non dissimile da quella che egli riceverebbe dagli enti obiettivi. Per raggiungere questo intento s'immagina che la superficie da rappresentare sia quella di un corpo opaco, illuminato da una sorgente luminosa, la quale di regola si suppone situata a distanza infinita, in una determinata direzione, talché i raggi luminosi (rettilinei) risultino fra loro paralleli (luce solare). Giova peraltro aggiungere che talvolta si è condotti anche a supporre che la sorgente luminosa sia a distanza finita, ma sempre ridotta a un punto (luce centrale).
In ogni caso, detta F la figura che si vuol rappresentare, i raggi luminosi sono, rispetto a F, in parte esterni, altri seganti, altri infine tangenti (o radenti). Il luogo dei punti di contatto dei raggi tangenti (o di radenza di quelli radenti) costituisce la cosiddetta (linea o regione) separatrice, in quanto separa la regione di F che si trova in luce da quella in ombra (ombra propria di F). Se poi la F si suppone in presenza di piani (o superficie) opachi (e tali, nella rappresentazione del , Monge, si suppongono di regola i piani di proiezione) il luogo dei raggi tangenti o radenti (i quali costituiscono il cosiddetto cilindro o cono d'illuminazione di F) sega codesti piani (o codeste superficie) secondo una linea chiusa, che delimita l'ombra portata di F.
Nel metodo del Monge la direzione della luce, supposta solare, s'individua, dando le due proiezioni (l′, l″) di uno qualsiasi dei raggi luminosi; e di regola si suppone che la luce provenga da un punto all'infinito della I regione, situato alle spalle e a sinistra (in alto) rispetto a chi, ritto su π1+, guardi π+2. È particolarmente usata, specialmente nel disegno di macchine (per la semplicità delle costruzioni cui dà luogo), la cosiddetta "luce a 45°", in cui entrambe le proiezioni di ogni raggio luminoso formano un angolo di 45° gradi con la linea di terra.
19. La parte di un solido che si trova in luce, non appare, a chi guarda da un dato punto, tutta egualmente illuminata; si ha un graduale passaggio dalle regioni in piena luce a quelle in ombra. La "teoria del chiaroscuro" si propone di riprodurre, sia pure in via approssimata, questi varî effetti di luce. A tal fine si tien conto del fatto che l'intensità dell'illuminazione di un elemento superficiale decresce, quando l'angolo ϑ che il suo piano forma con la direzione dei raggi luminosi decrese da π/2 a 0; e, precisamente, seguendo il Lambert, si ammette che, se 1 è l'intensità dell'illuminazione per ϑ = π/2, essa sia in generale espressa da sen ϑ, o, ciò che è lo stesso, da cos ω, se ω è l'angolo acuto formato dalla normale alla superficie nel punto considerato con la direzione dei raggi luminosi. Sopra una superficie qualsiasi f (x, y, z) = 0, tutti i punti di eguale illuminazione costituiscono una linea (detta isofota) che si ottiene segando la superficie stessa con altra (detta isofotoide) avente per equazione:
dove cos λ, cos μ, cos ν denotano i coseni direttori dei raggi luminosi.
Supposte segnate le isofote corrispondenti a valori di cos ω costituenti una progressione aritmetica avente per termini estremi 1 e 0, la parte illuminata della data superficie risulta decomposta in una serie di zone, ognuna delle quali è limitata da due isofote consecutive; queste zone vengono acquarellate con tinte sempre più scure, sino a raggiungere la linea d'ombra propria, che corrisponde a cos ω = 0; se le linee isofote si seguono a intervalli molto vicini, l'impressione che produce la figura risultante è assai prossima a quella che si riceverebbe dalla figura rappresentata.
Quando una superficie è illuminata da un punto L e guardata da un punto O essa presenta in generale dei "punti brillanti"; sono quei punti X tali che la corrispondente normale alla superficie risulti bisettrice dell'angolo LXO. Tale definizione è applicabile anche quando uno o entrambi i punti L, O si trovino all'infinito.
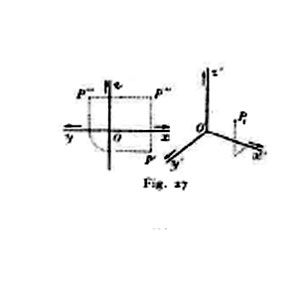
20. Assonometria. - Le due proiezioni, che di una figura F si considerano nella rappresentazione del Monge, ne determinano bensì gli elementi di forma e di grandezza, ma non ne forniscono sempre un'immagine rispondente a quella che è data dalla visione diretta. Perciò conviene spesso ricorrere a una terza proiezione, da un prefissato centro, sopra un quadro π, opportunamente situato rispetto ai due piani fondamentali π1, π2. Alla determinazione di questa terza proiezione bastano, teoricamente, le costruzioni elementari (nn. 7-9), ma il procedimento risulta in genere laborioso, cosicché appare opportuno cercare qualche metodo costruttivo più diretto e rapido. Tale è, nel caso della proiezione parallela, la cosiddetta assonometria. La figura obiettiva F s'immagina riferita a una terna di assi cartesiani ortogonali Oxyz (v. coordinate), di cui ad es., l'asse delle x sia la linea di terra della rappresentazione del Monge e quelli delle y, z siano le intersezioni di un dato piano di profilo π3 con π1, π2. Tutto allora si riduce a costruire l'immagine O′x′y′z′ di codesta terna sul quadro prefissato π e i tre segmenti ux, uy, uz (unità assonometriche), in cui si proietta su π l'unità di lunghezza obiettiva u, presa, rispettivamente, nelle direzioni dei tre assi x, y, z. Quando si conoscono questi elementi, è manifesto come si costruisca l'immagine P di ogni punto P, di cui si conoscano le proiezioni su π1, π2, π3 (fig. 27).
Gli assi assonometrici e le rispettive unità ux, uy, uz, si possono prefissare ad arbitrio sul quadro, e con ciò risulta determinata (a meno di una traslazione in una data direzione) la posizione di π rispetto ai piani fondamentali π1, π2 (e π3). Sussiste, invero, il seguente teorema del Pohlke: Fissati sul quadro, a partire da un qualsiasi punto O′, tre segmenti quali si vogliono (purché tali che non sia nullo né più di uno di essi, né più di uno degli angoli da essi formati, a due a due), questi tre segmenti si possono sempre considerare come proiezioni, secondo una determinata direzione, di tre segmenti fra loro uguali e a due a due ortogonali, uscenti da un punto O dello spazio.
Particolarmente usata è l'assonometria ortogonale (centro di proiezione a distanza infinita, nella direzione ortogonale al quadro), nella quale, per avere tre assi assonometrici distinti, bisogna prendere il quadro non parallelo ad alcuno dei tre assi obiettivi. Le intersezioni di questi col quadro costituiscono i vertici X, Y, Z del cosiddetto triangolo delle tracce (fig. 28), il quale risulta sempre acutangolo e ammette l'origine assonometrica O′ come baricentro (punto comune alle tre altezze). Sono "costanti fondamentali" dell'assonometria ortogonale: gli angoli α, β, γ, che gli assi x, y, z formano col quadro; i rispettivi coseni λ, μ, ν (rapporti di accorciamento), che dànno i rapporti delle tre unità assonometriche ux, uy, uz, all'unità obiettiva u; gli angoli ξ, η, ζ che gli assi assonometrici x′, y′, z′ formano a due a due. Sussistono fra queste costanti le relazioni fondamentali:
Se sono uguali due dei rapporti di accorciamento, tali risultano anche le corrispondenti costanti delle altre due terne e il triangolo delle tracce è isoscele. L'assonometria si dice in questo caso monodimetrica o dimetrica; mentre si chiama isometrica o monometrica, se i tre rapporti di accorciamento sono uguali (triangolo delle tracce equilatero); si dice, invece, anisometrica se i tre rapporti sono disuguali (triangolo delle tracce scaleno).
In ogni caso l'assonometria ortogonale risulta individuata (a meno della simmetria rispetto al quadro) quando si assegnino ad arbitrio il triangolo delle tracce (soggetto alla sola condizione di essere acutangolo) e l'unità obiettiva delle lunghezze.
L'assonometria ortogonale e, in casi speciali, quella obliqua sono largamente usate nella prospettiva. Per questa importante applicazione della geometria descrittiva, come pure per la fotogrammetria e per un cenno di gnomonica, v. le voci corrispondenti.
Cenni storici. - 21. La geometria descrittiva, come già si accennò dapprincipio, è sorta sul confluente di due correnti d'idee, aventi le loro origini in esigenze d'ordine artistico per l'una, d'ordine tecnico per l'altra. Il fenomeno della visione e la constatazione del propagarsi della luce in linea retta avevano, fin dall'antichità, suscitato studî sull'ottica e la catottrica, alcuni dei quali esistono tuttora e son dovuti a Euclide e ad altri matematici dell'evo antico. Avendo constatato come soltanto da tali studî (costituenti la primitiva letteratura sulla prospettiva) la pittura poteva trovare un solido fondamento razionale, vi si dedicarono con impegno eminenti artisti del Rinascimento, quali L. B. Alberti, P. della Francesca, L. Da Vinci, A. Dürer; e poco dopo si volsero allo stesso ordine di problemi alcuni distinti matematici, fra i quali va ricordato Guidobaldo del Monte, cui si deve la scoperta del "punto di concorso" o, come oggi si dice, del punto di fuga di un sistema di rette fra loro parallele. Fra tutti emerge un grande contemporaneo di R. Descartes e B. Pascal, G. Desargues (v.), che il Poncelet non esitò a qualificare per il "Monge del suo secolo"; mal compreso dai proprî contemporanei, esso appare oggi (per non citare che una delle sue benemerenze) come primo ideatore dell'assonometria ortogonale; poco dopo l'inglese Brook Taylor creava il metodo della proiezione centrale e lo svizzero J. H. Lambert, ignorando l'opera di questo) geniale matematico, si proponeva per conto suo di rendere la prospettiva indipendente dalla proiezione ortogonale.
D'altra parte, già molto prima gli architetti avevano avvertito il bisogno di delineare immagini verosimili delle costruzioni che balenavano alla loro fantasia: da ciò l'uso della pianta e dell'alzato d'un edificio, forma rudimentale del metodo della doppia proiezione ortogonale, di cui le prime vestigia furono rivelate da scavi eseguiti sulle rive del Nilo, e molteplici applicazioni si leggono nella grande opera di Vitruvio sull'architettura. Le ulteriori fasi di sviluppo di questo metodo vanno ricercate nei lavori dei più insigni ingegneri posteriori, sino a giungere ad A. F. Frézier, di cui La théorie et la pratique de la coupe des pierres et des bois (3 voll., Strasburgo 1737-39) è tuttora degna di ammirazione e di studio; e circa nello stesso tempo alcuni ingegneri militari gettavano le basi del metodo dei piani quotati, ausiliare prezioso in ogni lavoro di fortificazione. Il metodo della doppia proiezione ortogonale entrò a far parte della geometria verso il finire del sec. XVIII per opera di G. Monge, scienziato e uomo politico che brillò nell'epoca fortunosa della Rivoluzione francese, del consolato e del primo impero. La sua Géométrie descriptive (Parigi 1798) prodotto di un lungo pubblico insegnamento, tiene il primo posto nell'elenco delle opere sulla disciplina di cui ci occupiamo e giustifica pienamente la designazione di "metodo di Monge" per il primo dei procedimenti esposti nelle pagine precedenti. Grazie al concorso di collaboratori e discepoli - fra cui ci limitiamo a ricordare S.-F. Lacroix, J.-N.-P. Hachette, C. Dupin, C. Poncelet, M. Chasles, J. Olivier (al quale si deve l'uso metodico di ribaltamenti e rotazioni) - la nuova disciplina ottenne in Francia durante il sec. XIX considerevoli miglioramenti e notevoli applicazioni; degli uni e delle altre si può rendersi conto esaminando il grande Traité de géométrie descriptive (Parigi, 1862-64) di J. de la Gournerie.
22. È merito di V. Flauti, il più eminente discepolo di N. Fergola, di avere diffuso in Italia il nuovo ramo di geometria, dopo averne un po' modificati i concetti dottrinali e avere dato ad esso il nome di geometria di sito. A. Bordoni e G. Bellavitis, seguirono il suo esempio riuscendo a fare progredire quanto avevano appreso dalla Francia. D'altro canto notevoli contributi furono recati da matematici tedeschi: C. Weisbach concepì e pose su basi definitive l'assommetria ortogonale; K. Pohlke scoperse il teorema fondamentale dell'assonometria obliqua (n. 20); G. Hauck, sviluppò la prospettiva assonometrica e iniziò la fotogrammetria, che doveva poi essere sistematicamente esposta da F. Schilling.
Un posto eminente nello sviluppo della geometria descrittiva spetta al trattato di W. Fiedler (Die darstellende Geometrie, Lipsia 1871, 3ª ed. 1883-1888), ispirato al proposito di fondere la geometria descrittiva con la proiettiva. E a questo trattato di carattere rigidamente sintetico va, in qualche modo, contrapposto per il suo eclettismo quello del matematico francese A. Mannheim (Cours de geométrie descriptive, Parigi 1880), nel quale, accanto ai metodi geometrici puri, vengono largamente applicati quelli della geometria cinematica e della geometria infinitesimale. Durante il presente secolo la scienza di cui ragioniamo si accrebbe notevolmente per l'applicazione a essa di elevate corrispondenze geometriche fatta da E. Müller, come si apprende dalle sue Vorlesungen über darstellende Geometrie (I: Die linearen Abbildungen, rielaborato da E. Krupper, Lipsia-Vienna 1923; II: Die Zyklographie, a cura di J. L. Kramer, ibid. 1929). I metodi della geometria descrittiva furono estesi alla rappresentazione di figure dello spazio a quattro dimensioni.
Bibl.: La letteratura relativa alla geometria descrittiva è straordinariamente ricca, fatto che si spiega sia considerandone i caratteri teorico e pratico, sia tenendo conto del fatto che essa è materia d'insgnamento in molti ordini di scuole; oltre i trattati classici già ricordati, ci limitiamo a citare i seguenti corsi di lezioni, dovuti a geometri italiani: D. Regis, Corso di applicazioni della geometria descrittiva, fascicoli 5, Torino 1895-1904; F. Enriques, Lezioni di geometria descrittiva, a cura di U. Concina, Bologna 1902, 4ª ed., 1925; G. Loria, Metodi della geometria descrittiva, Milano 1905, 3ª ed. 1912; id., Poliedri, curve e superfici secondo i metodi della geometria descrittiva, Milano 1925; Complementi di geometria descrittiva, Milano 1924; id., Vorlesungen über darstellende Geometrie, voll. 2, Lipsia 1907, 1913; G. Fano, Lezioni di geometria descrittiva, Torino 1914, 3ª ed. 1925. - Per la storia: G. Loria, Storia della geomeria descrittiva dalle origini sino ai nostri giorni, Milano 1921.