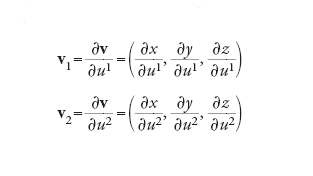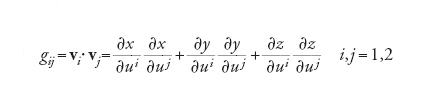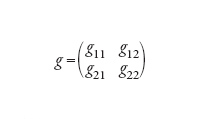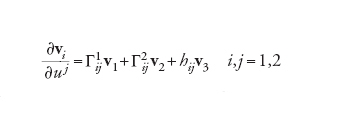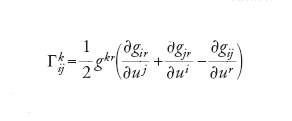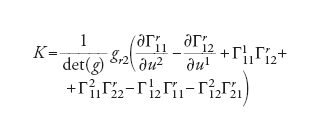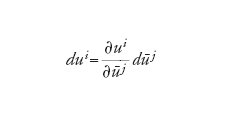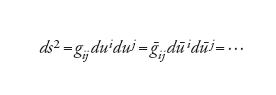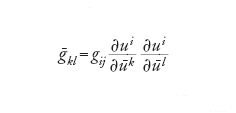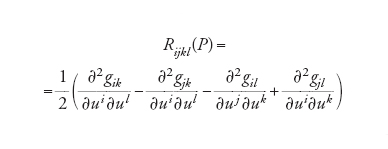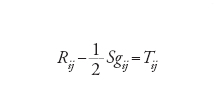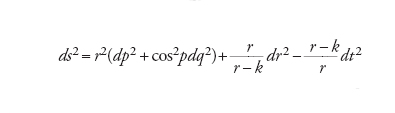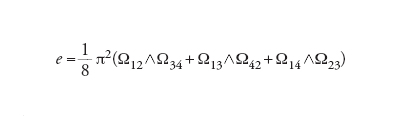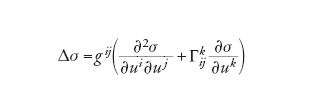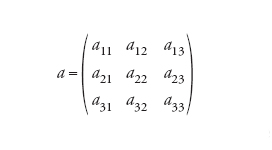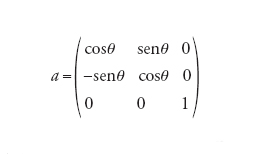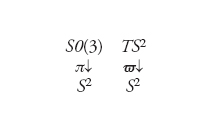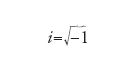Geometria differenziale

Geometria differenziale

La geometria differenziale, un ramo della matematica in cui il calcolo differenziale e integrale è applicato allo studio degli oggetti geometrici, è antica quanto il calcolo stesso. Tuttavia, non vi fu una sistemazione organica della geometria differenziale delle superfici fino al 1827, anno in cui Carl Friedrich Gauss pubblicò le sue Disquisitiones circa superficies curvas. Gauss riconobbe l'importanza della geometria intrinseca delle superfici, e generalmente si conviene che la geometria differenziale, così come è nota al giorno d'oggi, abbia avuto in lui il suo iniziatore. Egli fu seguito da Georg Friedrich Bernhard Riemann, il quale introdusse quella che oggi è nota come metrica riemanniana; in effetti egli considerò metriche più generali che formarono l'oggetto della dissertazione di Paul Finsler nel 1918. Nel lavoro pubblicato nei "Mathematische Annalen", Gregorio Ricci-Curbastro e Tullio Levi-Civita svilupparono il calcolo tensoriale come un potente strumento per la geometria riemanniana. Era precisamente ciò di cui Albert Einstein aveva bisogno per descrivere la sua teoria della relatività generale e ciò suscitò interesse nei confronti della geometria riemanniana. Nel 1917 Levi-Civita introdusse in quest'ultima la nozione di parallelismo, attribuendo significato geometrico al calcolo tensoriale formale.

Nel 1918, Hermann Weyl sviluppò la geometria differenziale affine, basata esclusivamente sulla nozione di parallelismo e non sulla metrica riemanniana. Assumendo il punto di vista della teoria degli invarianti, egli creò nel 1921 la teoria delle connessioni proiettive e conformi. Il suo punto di vista, adottato da Luther P. Eisenhart, Oswald Veblen e Tracy Y. Thomas, dominò la geometria differenziale negli Stati Uniti negli anni Venti e Trenta.

In una serie di lavori pubblicati tra il 1923 e il 1925, Élie Cartan sviluppò anche la teoria delle connessioni affini, proiettive e conformi secondo il punto di vista del Programma di Erlangen di Felix Klein. Il metodo del riferimento mobile, creato da Gaston Darboux e ampiamente sviluppato da Cartan nella sua teoria delle connessioni, fu un precursore della teoria degli spazi fibrati. Combinando l'algebra di Grassman con il calcolo differenziale, Cartan inventò un potente strumento di calcolo noto come calcolo delle forme differenziali. Da allora esso è diventato indispensabile in topologia, in geometria algebrica e nella teoria delle funzioni di più variabili complesse, così come in geometria differenziale.

Il lavoro di Cartan sui gruppi di Lie, in particolare sui gruppi di Lie semplici e sulla geometria differenziale, culminò nel 1926 nella sua scoperta degli spazi riemanniani simmetrici. Questi ultimi offrono una naturale generalizzazione della superficie sferica nello spazio euclideo e del disco unitario nel piano complesso con la metrica di Poincaré. Essi sono diventati sempre più importanti, dato il ruolo essenziale che giocano nella teoria delle rappresentazioni unitarie e in altri campi della matematica.

Eccettuati i lavori di Cartan, la geometria differenziale negli anni Venti si occupava soprattutto di superfici nello spazio euclideo 3-dimensionale e di proprietà locali di varietà riemanniane. Ma l'orientamento verso la geometria differenziale globale (cioè la geometria differenziale che riguarda le proprietà delle varietà nel loro complesso) cominciò lentamente all'inizio degli anni Trenta con la dissertazione di Georges de Rham pubblicata nel 1931, nella quale veniva discusso il teorema che da allora prese il suo nome.

Un'importante classe di varietà complesse con metrica riemanniana compatibile fu scoperta da Jan A. Schouten e David van Dantzig nel 1929 e da Erich Kähler nel 1932. Questa classe di varietà, chiamate oggi kähleriane, comprende quelle algebriche: la teoria di William Hodge degli integrali armonici è più efficace quando è applicata a varietà kähleriane compatte.

Il teorema globale più famoso nella geometria differenziale classica delle superfici è la formula di Gauss-Bonnet (1848). Applicata a una superficie orientabile chiusa, essa afferma che l'integrale della curvatura gaussiana è uguale a 2π volte il numero di Eulero della superficie. La formula fu generalizzata a ipersuperfici chiuse nello spazio euclideo di dimensione arbitraria da Heinz Hopf (1925), a sottovarietà chiuse di spazi euclidei da Carl B. Allendoerfer e anche da Werner Fenchel (1940), e infine a varietà riemanniane chiuse arbitrarie da Allendoerfer stesso e André Weil nel 1943. Ma la semplice dimostrazione data da Shiing-Shen Chern nel 1944 conteneva la trasgressione, diventata essenziale nella teoria delle classi caratteristiche.

Geodetiche e superfici minime

Lo studio delle geodetiche è uno degli argomenti più antichi in geometria differenziale. Dato che le geodetiche appaiono come punti critici di certi funzionali, il calcolo delle variazioni, che risale a Leonhard Euler e Joseph-Louis Lagrange, è uno strumento naturale di ricerca. L'esistenza di geodetiche chiuse, in relazione a problemi dinamici, è stata una delle questioni centrali della geometria differenziale fin dal tempo di Henri Poincaré, il quale dimostrò l'esistenza di una geodetica chiusa su ogni superficie convessa (1905). Questo risultato fu esteso da George D. Birkhoff a dimensioni più elevate. Il calcolo delle variazioni in grande, iniziato da Poincaré e Birkhoff, fu sistematicamente sviluppato nella forma moderna da Marston Morse. Lavori recenti sulle geodetiche chiuse si basano in modo essenziale sulla teoria di Morse o su sue varianti. Inoltre, studi profondi sulle geodetiche condussero Harry Rauch, Wilhelm Klingenberg, Marcel Berger e altri a una migliore comprensione delle varietà riemanniane a curvatura positiva.

La teoria delle superfici minime (superfici di area minima spezzate da una data curva nello spazio) ebbe inizio con Lagrange come un'ulteriore applicazione del suo calcolo delle variazioni. Al primo stadio di sviluppo, Gaspard Monge, Jean-Baptiste M. C. Meusnier, Adrien-Marie Legendre, Pierre Ossian Bonnet, Riemann, Karl Weierstrass, Hermann A. Schwarz, Eugenio Beltrami e Lie contribuirono alla teoria. Weierstrass e Schwarz stabilirono le relazioni con la teoria delle funzioni. Joseph Antoine Plateau dimostrò sperimentalmente che possono essere realizzate con pellicole di sapone intingendo un filo di ferro, modellato come una curva chiusa sghemba, in una soluzione di sapone (1873). Il problema di Plateau è di dimostrare matematicamente l'esistenza di superfici minime con un'assegnata curva al contorno. Il problema fu risolto per curve di Jordan da Tibor Radó nel 1930 e, indipendentemente, da Jesse Douglas nel 1931. I due problemi sulle superfici minime che attrassero di più l'attenzione sono quello di Plateau e quello di Sergei N. Bernštein. Quest'ultimo è un problema su ipersuperfici minime negli spazi euclidei di dimensione più alta. Sia y=f(x₁,…,x_n) definita per tutti i valori di (x₁,…,x_n)∈ℝⁿ e supponiamo che il suo grafico sia una sottovarietà minima dello spazio euclideo (n+1)-dimensionale. Bernštein mostrò che il grafico è necessariamente un piano per n=2 (1927). Il problema di estendere il risultato di Bernštein a dimensioni più alte ebbe un esito sorprendente: la generalizzazione per n=3, data da Ennio de Giorgi (1965), per n=4, data da Frederick J. Almgren (1966), e per n=5, 6, 7, data da James Simons (1968), fu seguita dalla scoperta di controesempi per n≥8 fatta da Enrico Bombieri, de Giorgi ed Enrico Giusti (1969). In anni recenti numerosi risultati sono stati ottenuti non solo per superfici minime negli spazi euclidei 3-dimensionali, ma anche per sottovarietà minime in spazi euclidei a dimensione più elevata, in sfere e in altri spazi simmetrici.

Studio della curvatura gaussiana

Presentiamo ora una dimostrazione in termini moderni del theorema egregium di Gauss allo scopo di illustrare alcune tecniche peculiari della geometria differenziale. Nello spazio euclideo tridimensionale con coordinate x,y,z, un'equazione in x,y,z generalmente individua una superficie, anche se spesso è più conveniente parametrizzare parte di essa mediante una coppia ausiliare di coordinate. Per semplicità, denoteremo queste coordinate con u¹,u². Tale notazione, che può sembrare all'inizio confusa, risulta in realtà molto utile; gli esponenti 1 e 2 del simbolo u sono indici che servono a distinguere le varie coordinate. Un punto generico della superficie è individuato dal vettore posizione v=(x(u¹,u²), y(u¹,u²), z(u¹,u²)). I vettori tangenti alle curve ottenute ponendo costanti sono dati da

[1] formula

e i prodotti scalari

[2] formula

individuano le lunghezze di v₁ e di v₂ e l'angolo tra di essi. Le funzioni g_ij servono a definire la prima forma quadratica fondamentale sulla superficie. Si tratta di un'espressione, introdotta da Gauss, che contiene implicitamente il metodo per misurare le distanze usando le coordinate u¹, u². Indichiamo con g la seguente matrice:

[3] formula.

Sia v₃ il campo vettoriale unitario normale alla superficie; allora i tre campi vettoriali v₁, v₂, v₃ costituiscono un sistema di riferimento in ogni punto. Differenziando v₁ e v₂ si ha:

[4] formula.

Le quantità Γⁱ_jk (ci sono 6 termini diversi in quanto per es., Γⁱ₁₂=Γⁱ₂₁) sono detti simboli di Christoffel, mentre gli h_ij (ce ne sono 3 diversi in quanto per es., h₁₂=h₂₁) danno un'espressione analitica per la seconda forma quadratica fondamentale, un'espressione (anch'essa introdotta da Gauss) che contiene informazioni sulla curvatura gaussiana K della superficie.

Il theorema egregium segue da due formule famose che possono verificarsi facilmente. La prima è la seguente:

[5] formula;

essa esprime i simboli di Christoffel direttamente in termini delle funzioni g_ij. In questa, e nelle formule successive, per alleggerire le notazioni si applica l'usuale convenzione secondo la quale un indice ripetuto in ogni addendo (in questo caso r) sostituisce una sommatoria ∑_r. I coefficienti g^kr sono gli elementi della matrice inversa di [3]. La seconda formula, che può essere verificata facilmente, è la seguente:

[6] formula.

Essa fornisce la dimostrazione del teorema in quanto esprime la curvatura gaussiana mediante i simboli di Christoffel, i quali, a loro volta, sono espressi dalla [5] in funzione dei g_ij e delle loro derivate.

Un aspetto fondamentale della geometria differenziale consiste nell'interazione tra le cosiddette proprietà locali e globali. La curvatura di una superficie o di una curva si può determinare esaminando soltanto una piccola regione intorno al punto, ma è chiaro che questa nozione di tipo locale può influire sull'andamento della curva o della superficie nella loro globalità. Per esempio, proprio la curvatura della sfera è responsabile della sua chiusura su se stessa e quindi del fatto che la sua area sia finita. Anche la teoria delle geodetiche mette in risalto la differenza tra locale e globale. In una regione sufficientemente piccola di una superficie, la geodetica tra due punti è l'unica curva che individua il percorso di minima distanza da un punto all'altro; dal punto di vista analitico, si tratta della traiettoria di una particella le cui coordinate uⁱ(t) verificano le seguenti equazioni alle derivate parziali del secondo ordine:

[7] ü^k+Γ^k_ijuⁱu^j=0 k=1,2

dove i punti sopra le lettere indicano le derivate rispetto a t. Invece, se la regione considerata si ingrandisce si viene a perdere la proprietà di unicità, come nel caso della sfera, in cui le geodetiche coincidono con i cerchi massimi; lo studio di altre superfici su cui le geodetiche si richiudano su se stesse, come nel caso della sfera, rappresenta comunque un problema affascinante.

La teoria precedente è illustrata nel teorema di Gauss-Bonnet, che classicamente costituisce il punto d'arrivo di molti corsi universitari di introduzione alla geometria differenziale. La sua prima formulazione, dovuta a Gauss, si applica a un triangolo geodetico inscritto in una superficie, vale a dire una regione T delimitata da tre geodetiche. Gli angoli interni α, β, γ di T si possono misurare (in radianti) considerando le tangenti nei vertici alle curve che costitutiscono i lati e si ha

[8] ∫_TKdA=α+β+γ−π

dove l'integrale al primo membro è approssimato dalla somma dei prodotti di K per l'area di regioni infinitesime. Per esempio, nel caso di una sfera di raggio r, K è uguale a 1/r in ogni punto e il primo membro della [8] coincide con l'area del triangolo divisa per r; quindi l'area di un triangolo sferico è proporzionale alla differenza tra la somma dei suoi angoli e 180° (ossia π radianti). La formula [8] è stata generalizzata da Bonnet al caso di curve qualsiasi, non necessariamente geodetiche.

Un teorema più completo si ottiene dividendo una superficie chiusa Σ dello spazio tridimensionale in un certo numero di triangoli geodetici e sommando il contributo [8] di ciascuno di essi. Ne segue che

[9] ∫_ΣKdA=2πχ

dove il numero χ denota la caratteristica di Eulero di Σ. La [9] è la più semplice di una famiglia considerevole di equazioni che mettono in relazione la curvatura di un oggetto con la sua topologia. Si osservi inoltre che la [9] non cambia quando viene variata la metrica assegnata tramite la prima forma fondamentale della superficie.

Dal teorema di Gauss-Bonnet si deduce che la sfera è l'unica superficie chiusa a curvatura gaussiana costante positiva, mentre il toro è l'unica superficie chiusa a curvatura identicamente nulla. Esistono, invece, molte superfici a curvatura gaussiana costante negativa, che presentano quella che viene chiamata una geometria iperbolica. Ne è un esempio noto la pseudosfera formata dalla rotazione di una curva particolare, la trattrice; ma per avere una panoramica completa si devono considerare modelli più astratti, essendo la geometria iperbolica interamente caratterizzata dalla matrice (g_ij). Ponendo x=u¹ e y=u², una soluzione dell'equazione K≡−1 (vale a dire K uguale a −1 per ogni valore di x e di y) è data semplicemente da g₁₁=g₂₂=1/y² e g₁₂=0. Un modello per tale metrica è dato dal semipiano superiore formato da tutti i punti (x,y) con y positivo. In questo modello, dovuto a Poincaré, le geodetiche sono archi di circonferenze con centro sull'asse orizzontale oppure rette verticali, e l'area di un triangolo iperbolico è data da π meno la somma dei suoi angoli (in radianti).

Dimensioni superiori

Il calcolo differenziale sulle varietà si basa sull'equivalenza di diversi sistemi di coordinate che rappresentano i punti su uno spazio astratto di dimensione n. Dati due tali sistemi,

[10] (u¹,…,uⁿ), (u-¹,…,u-ⁿ)

si assume che esistano n equazioni del tipo

[11] uⁱ=uⁱ(u-¹,…,u-ⁿ) 1≤i≤n

che esprimono un sistema in funzione dell'altro. In questo contesto, l'espressione duⁱ, che prende il nome di covettore o 1-forma, rappresenta la velocità di cambiamento dell'i-esima coordinata uⁱ in tutti i possibili punti e in tutte le direzioni possibili e varia al mutare dei sistemi di coordinate in accordo con la regola della catena:

[12] formula.

Una metrica riemanniana è definita assegnando una matrice n×n simmetrica definita positiva (g_ij), (g-_ij) per ogni sistema di coordinate in modo tale che

[13] formula

sia una forma quadratica invariante che è la naturale generalizzazione della prima forma quadratica fondamentale per una superficie. Ne segue che (g_ij) e (g-_ij) sono legate dalla seguente relazione:

[14] formula.

Questa regola di trasformazione tratta la metrica riemanniana come un tensore di tipo particolare. Si può definire la lunghezza di una curva integrando l'espressione ds=√(g_ijduⁱdu^j) e di conseguenza calcolare la distanza tra due punti qualsiasi appartenenti allo spazio astratto che si sta prendendo in considerazione. L'equazione [5] ci permette di definire i simboli di Christoffel Γⁱ_jk come nel caso delle superfici, con l'unica differenza che ora gli indici variano da 1 a n. L'analogo della [6] nel caso delle dimensioni superiori non porta a un'unica funzione scalare K, ma alle componenti R_ijkl di un oggetto di grande significato chiamato tensore di curvatura riemanniano. Le funzioni R_ijkl si trasformano in modo analogo alla formula [14] e dato un punto P è possibile individuare un sistema di coordinate tale che il loro valore sia il seguente:

[15] formula.

Le simmetrie che emergono da questa equazione possono essere usate per dimostrare che R_ijkl(P) è determinato esattamente da n²(n²−1)/12 numeri (quindi da un solo numero quando n=2).

Uno dei concetti più importanti dell'analisi tensoriale, quello di connessione, era già implicito nella definizione dei simboli di Christoffel; esso fornisce un metodo per valutare la velocità con cui i vettori e i tensori variano sulla varietà; l'operatore ∇ dato da

[16] ∇duⁱ=Γ^k_ijdu^jdu^k

prende il nome di connessione di Levi-Civita. Esso viene usato per introdurre la nozione di parallelismo, che permette di stabilire quando un tensore è costante lungo una curva negli spazi considerati da Riemann. Nel caso delle superfici nello spazio euclideo tridimensionale, la connessione di Levi-Civita coincide con la componente tangenziale della derivazione ordinaria in ℝ³ e ciò spiega la presenza dei simboli di Christoffel nella formula [4].

Le teorie della relatività di Einstein si basano sul fatto che l'Universo è visto come uno spazio di dimensione 4 che comprende le tre usuali coordinate spaziali x,y,z e il tempo t; il modello per la teoria della relatività speciale è lo spazio piatto di Minkowski, ossia ℝ⁴ con coordinate u¹=x, u²=y, u³=z, u⁴=ct (c è la velocità della luce) e tensore metrico dato da g₁₁=g₂₂=g₃₃=1, g₄₄=−1 e g_ij=0 se i≠j. Nella teoria della relatività generale, le funzioni g_ij variano da punto a punto e la metrica si dice pseudoriemanniana, in quanto la forma quadratica [13] assume dei valori negativi; infatti il percorso di un raggio di luce è una geodetica lungo la quale la distanza è nulla. Nel caso della dimensione n=4, esattamente 10 delle 20 componenti del tensore di curvatura riemanniano possono essere ricavate dal tensore di Ricci definito nel modo seguente:

[17] R_ij=R_ijklg^kl.

È degno di nota il fatto che i tensori R_ij e g_ij siano esattamente dello stesso tipo: sono entrambi simmetrici, cioè non variano scambiando tra loro i e j. Insieme caratterizzano le equazioni di Einstein,

[18] formula

dove S=R_ijg^ij è la curvatura scalare e T_ij è un tensore determinato dall'energia e dalla quantità di moto della materia nell'universo. Una delle soluzioni esplicite più semplici della [18] è la metrica di Schwarzschild,

[19] formula

dove r è la coordinata radiale e k è costante. La [19] modella il campo gravitazionale di una stella o di un buco nero, entrambi sfericamente simmetrici, in un universo vuoto, ossia con T_ij=0; l'espressione tra parentesi rappresenta una metrica sulla sfera. Come molte altre metriche interessanti dal punto di vista della fisica, la [19] è determinata da una matrice diagonale (vale a dire g_ij=0 se i≠j).

Nell'ipotesi in cui M sia una varietà riemanniana chiusa di dimensione n, si perviene ad alcune generalizzazioni del teorema di Gauss-Bonnet. Dal punto di vista puramente topologico, una varietà può essere costruita in vari modi mediante una collezione di celle di dimensioni diverse. Per esempio, un ipercubo di ℝ⁴ può essere visto come una varietà topologica di dimensione tre (si richiede solo che le funzioni di transizione siano continue) con 16 vertici, 32 spigoli, 24 facce e 8 celle di dimensione 3. Allora la definizione della caratteristica di Eulero si può estendere ponendo χ=∑ⁿ_p=0(−1)^pc_p, dove c_p è il numero delle celle di dimensione p; quindi nel caso dell'ipercubo si ha c₀=16, c₁=32, c₂=24, c₃=8, e pertanto χ=0, il che è in realtà vero per ogni varietà orientata di dimensione dispari. Infatti, χ risulta essere anche uguale a ∑ⁿ_p=0(−1)^pb_p, dove i b_p sono i numeri di Betti ‒ così chiamati da Poincaré in onore di Enrico Betti ‒ che, a differenza dei c_p, dipendono solo dalla topologia della varietà. Un teorema di Chern esprime χ nel caso generale come integrale di una quantità e definita tramite il tensore di curvatura; per esempio, nel caso di dimensione 4, è data da

[20] formula

dove Ω_ij=R_ijkldu^k∧du^l. L'espressione du^k∧du^l può essere considerata un'abbreviazione del prodotto antisimmetrico du^kdu^l−du^ldu^k ed è una 2-forma definita nel sistema di coordinate considerato. Viceversa, la legge di trasformazione tensoriale valida per R_ijkl fa sì che e sia una 4-forma definita globalmente, vale a dire per tutti i punti della varietà M, e di conseguenza la rende una quantità che può essere integrata su M.

I numeri di Betti sulla varietà M si calcolano, a partire dai teoremi di de Rham e di Hodge, usando le forme differenziali. Infatti, b_p coincide con la dimensione dello spazio delle forme armoniche, vale a dire delle soluzioni dell'equazione Δσ=0, dove σ è una p-forma e Δ è una generalizzazione dell'operatore di Laplace. Per p=0, σ è una funzione ordinaria e la definizione

[21] formula

coinvolge la connessione di Levi-Civita definita nella [16]. Il secondo membro della [21] non dipende dal sistema di coordinate, e ciò mostra come si possano introdurre in modo naturale gli operatori differenziali sulle varietà . Nel caso in cui M sia chiusa, connessa e orientata, b₀ e b_n sono entrambi uguali a 1; più in generale b_p=b_n−p, da cui segue subito che se n è dispari allora χ=0. Tenendo conto che ogni forma armonica è un autovettore di Δ con autovalore nullo, l'insieme di tutti gli autovalori (cioè i numeri λ per cui esistono soluzioni dell'equazione differenziale Δσ=λσ) prende il nome di spettro di M. Il modo in cui una metrica riemanniana è determinata dal suo spettro costituisce un problema molto importante a cui si riferisce la famosa domanda di Mark Kac: si può sentire la forma di una varietà?

L'equazione Δσ=0 per una p-forma con p≥1 equivale alla coppia di equazioni differenziali del primo ordine dσ=0 e d*σ=0, dove d e d* sono particolari operatori che nel caso p=1 generalizzano rispettivamente i ben noti rotore e divergenza dell'analisi vettoriale; d è la differenziazione esterna e, a differenza di d*, può essere definita indipendentemente dalla metrica. Nonostante ciò, l'operatore differenziale ora considerato essenziale è quello di Dirac, che si definisce tramite la teoria delle algebre di Clifford e dal quale possono essere dedotti d, d* e tanti altri operatori differenziali. Gli spazi delle soluzioni delle equazioni differenziali che ne seguono dipendono, in generale, dalla scelta della metrica riemanniana, anche se le loro dimensioni determinano degli interi, detti indici, che sono analoghi alla caratteristica di Eulero e si possono esprimere tramite quantità puramente topologiche usando il teorema dell'indice di Michael F. Atiyah e Isadore M. Singer.

Gruppi e fibrati

La sfera, il piano euclideo e il semipiano superiore (introdotto nel paragrafo 3)sono modelli di superfici a curvatura costante. Ci sono modi diversi di interpretare il concetto di curvatura costante in dimensioni superiori e ciò ha fatto scaturire un'intera serie di problemi interessanti. Innanzitutto si potrebbe richiedere che il tensore di curvatura non cambi da punto a punto; tale proprietà si verificherebbe, per esempio, se per ogni coppia di punti P,Q sulla varietà esistesse una trasformazione che mandi P in Q e che conservi le distanze, vale a dire un'isometria. Nell'ambito della geometria riemanniana le varietà che ammettono tali isometrie prendono il nome di spazi omogenei e molti risultati sono più facili da capire in questo caso; per esempio, vi sono varietà che pur non essendo omogenee sono costruite in modo semplice a partire dagli spazi omogenei; è stata inoltre sviluppata una teoria molto ricca sulle metriche di Einstein e sull'operatore di Dirac sullo spazio totale dei fibrati vettoriali su spazi omogenei.

Uno degli spazi omogenei più facili da descrivere è la sfera ordinaria S², luogo dei punti dello spazio euclideo ℝ³ aventi distanza unitaria dall'origine. Ogni rotazione di ℝ³ intorno all'origine è una isometria che può far corrispondere due punti qualsiasi della sfera. Siano P₁,P₂,P₃ i punti della sfera S² rispettivamente di coordinate (1,0,0), (0,1,0), (0,0,1), posti sugli assi cartesiani. Ogni rotazione può essere rappresentata da una matrice quadrata di ordine 3,

[22] formula,

dove le righe esprimono nell'ordine le coordinate dei punti immagine mediante a di P₁,P₂,P₃; per esempio (a₃₁,a₃₂,a₃₃)=(0,0,1)a in accordo con la regola del prodotto di matrici. Ne segue che le righe di a formano una base ortonormale di vettori per ℝ³ (vale a dire sono vettori unitari a due a due ortogonali) e il suo determinante è uguale a 1. L'insieme delle rotazioni di ℝ³ intorno all'origine, che normalmente si indica con SO(3), è un gruppo di Lie, ossia ha una struttura di varietà liscia compatibile con la legge del prodotto di due matrici, dove per prodotto ab di due rotazioni si intende la rotazione in cui a è seguita da b. Le rotazioni intorno all'asse passante per l'origine e per il polo nord P₃ sono del tipo

[23] formula,

e formano un sottogruppo H di SO(3), che rappresenta quindi il gruppo delle rotazioni (con angolo θ variabile) del piano equatoriale. Data una matrice b di SO(3), le rotazioni aventi la stessa terza riga di b sono esattamente quelle della forma ab con a in H; queste formano ciò che si chiama un laterale, indicato in modo naturale Hb. Tale situazione si descrive schematicamente mediante il primo dei due diagrammi seguenti:

[24] formula

in cui π indica l'applicazione che associa a ogni matrice b la sua terza riga. Ogni laterale è quindi la controimmagine π⁻¹(Q) di un punto Q qualsiasi della sfera (la notazione π⁻¹(Q) indica tutte le matrici b che π manda in Q) e coincide con una circonferenza. Dato Q, una matrice b di π⁻¹(Q) è determinata dalle sue prime due righe, che rappresentano le immagini di P₁,P₂ mediante b. Se identifichiamo P₁ e P₂ con i vettori tangenti alla sfera in P₃ otteniamo che ogni matrice b in SO(3) è data semplicemente da una coppia ortonormale di vettori tangenti a S² nel punto π(b).

L'applicazione π permette di rappresentare SO(3) come un fibrato sulla sfera le cui fibre sono le controimmagini π⁻¹(Q) al variare di Q. Più precisamente, un fibrato è determinato da tre varietà E,F,M e da un'applicazione π: E→M definita in modo che ogni punto Q di M appartenga a una regione U tale che π⁻¹(Q) si possa identificare con il prodotto U×F; in altri termini, lo spazio totale E è localmente il prodotto di F con la base M. Il primo diagramma della [24] prende il nome di fibrato principale in quanto ogni fibra può essere vista come la copia di un gruppo (in questo caso H). Un altro esempio di fibrato, ma di tipo diverso dal precedente, è il fibrato tangente a S² rappresentato dal secondo diagramma della [24], in cui la fibra ω⁻¹(Q) è lo spazio tangente a S² in Q o, in modo equivalente, il complemento ortogonale Q^⊥ di Q in ℝ³. Si tratta in questo caso di un fibrato vettoriale di rango 2, poiché F è uno spazio vettoriale di dimensione 2. I due fibrati della [24] sono fortemente collegati, dato che ogni fibra del fibrato principale è costituita da basi ortonormali della fibra corrispondente del fibrato vettoriale. Più in generale, su ogni varietà liscia M può essere definito in modo astratto lo spazio tangente TM, mentre la scelta di un fibrato principale opportuno dipende dalla struttura che si sta considerando.

Varietà e topologia

Fin dalla scoperta del teorema di Gauss-Bonnet, l'interazione tra curvatura e topologia è stata oggetto di studio continuo. È tipico chiedersi se una varietà chiusa possa o meno ammettere una metrica riemanniana con tensore di curvatura assegnato. A questo proposito, ricordiamo le ricerche di Sumner B. Myers e Solomon Bochner e quelle di Richard Schoen. Le prime hanno portato a teoremi secondo i quali se il tensore di Ricci è positivo in modo analogo alla metrica [13] allora la varietà è chiusa e il suo primo numero di Betti b₁ si annulla; le seconde hanno visto la soluzione del problema di Yamabe, in base al quale ogni metrica riemanniana su una varietà chiusa può essere moltiplicata per una funzione positiva in modo da ottenere una metrica la cui curvatura scalare sia costante.

Riveste particolare interesse, sia per i matematici sia per i fisici, la classificazione delle varietà riemanniane dette di Einstein. Mentre questo discorso è relativamente facile in dimensione 2 e 3, non è neppure noto se le uniche varietà di dimensione 4 chiuse con tensore di Ricci nullo siano solo i due esempi che derivano dalla geometria complessa. La curvatura delle varietà riemanniane di dimensione 4 è particolarmente interessante per il fenomeno dell'autodualità che divide in due parti la metà del tensore R_ijkl complementare al tensore di Ricci. La teoria dei twistors, introdotta da Roger Penrose, fa sì che metriche speciali possano essere costruite usando tecniche proprie della teoria delle funzioni complesse. In dimensioni superiori, un problema più trattabile è quello della classificazione delle metriche di Einstein sugli spazi omogenei; attualmente, invece, l'attenzione è rivolta allo studio del caso più generale dei biquozienti F G/H, che sono varietà definite tramite laterali doppi determinati da due sottogruppi F,H di un gruppo di Lie G. Il caso particolare in cui F sia finito e G/H uno spazio simmetrico è il problema degli space forms generalizzati affrontato da Joseph A. Wolf. In questo momento alcune ricerche sono incanalate verso esempi molto speciali di metriche di Einstein, le cosiddette metriche con olonomia eccezionale, la cui esistenza è stata ipotizzata da Berger nel 1955.

Due classi di varietà molto studiate in geometria differenziale sono le varietà quasi simplettiche e quelle quasi-complesse. Le prime sono determinate da una forma bilineare ω antisimmetrica non degenere su ogni spazio tangente, le seconde da un isomorfismo J su ogni spazio tangente che mimi la moltiplicazione per

dei numeri complessi. Devono essere di dimensione pari e il prefisso quasi si toglie se esistono coordinate compatibili con ω e J. Ne segue che una varietà simplettica di dimensione 2n è caratterizzata dall'esistenza di una 2-forma ω per cui ωⁿ è non nulla in ogni punto e dω=0. Tali varietà si presentano in modo naturale come spazio delle configurazioni dei sistemi meccanici e sono spesso associate all'azione di gruppi di Lie. Ogni superficie orientata Σ di ℝ³ è una varietà kähleriana, vale a dire una varietà che abbia contemporaneamente una struttura riemanniana, una complessa e una simplettica compatibili fra loro in modo opportuno. Il tensore J è definito su Σ mediante la rotazione di 90⁰ dei vettori di ogni spazio tangente, dopo aver deciso se scegliere l'andamento orario o quello antiorario. Tutto ciò è legato a un noto teorema, in cui si afferma che è sempre possibile determinare, in un intorno di ogni punto di M, un sistema di coordinate x=u₁, y=u₂ in modo tale che g₁₁=g₂₂ e g₁₂=0, da cui

[25] ds²=E(dx²+dy²).

La funzione z=x+iy funge allora da coordinata complessa su Σ. Esempi significativi di varietà kähleriane di dimensione superiore a 2 sono dati dalle sottovarietà dello spazio proiettivo complesso ℙⁿ(ℂ), il cui studio costituisce una buona parte della geometria algebrica. La dimostrazione da parte di Shing-Tung Yau di una congettura di Eugenio Calabi determina l'esistenza di una grande famiglia di varietà kähleriane chiuse con tensore di Ricci nullo. In dimensione 4 ciascuno di questi spazi equivale, come varietà liscia, al toro di dimensione 4 oppure alla superficie K3, una particolare varietà con caratteristica di Eulero χ=24. La superficie K3 appartiene anche a un'altra classe ristretta di varietà kähleriane, le cosiddette varietà iperkähleriane, che ammettono alcune strutture kähleriane compatibili con una metrica fissata. La dimensione di una varietà iperkähleriana è sempre 4m con m intero e il prodotto mχ è divisibile per 24. La teoria delle varietà simplettiche e complesse, considerata come argomento a sé stante, è molto diversa dalla teoria delle varietà riemanniane; non esistono infatti concetti analoghi a quello del tensore di curvatura e quindi è necessario imporre strutture addizionali. In generale, è difficile determinare se e quando una data varietà liscia possa essere simplettica e/o complessa; devono essere soddisfatte innanzi tutto alcune condizioni topologiche: per esempio, ogni varietà simplettica chiusa deve avere b₂≠0.

Si sono avuti progressi fondamentali nel caso delle varietà lisce di dimensione 4 grazie alla formulazione matematica ‒ da parte di Simon K. Donaldson, Andreas Floer, Edward Witten e altri ‒ delle teorie di gauge, introdotte dai fisici negli anni Sessanta. La controparte matematica di un campo di gauge è il tensore di curvatura di una connessione, o potenziale di gauge, definito su un fibrato particolare su una varietà M le cui fibre possono essere delle circonferenze. Le connessioni sono studiate in relazione alla geometria dello spazio totale E del fibrato e, nel caso di dimensione 4, si ottengono in modo naturale in termini di una equazione differenziale non lineare del primo ordine imponendo una condizione sulla curvatura. Con appropriate ipotesi le classi di equivalenza delle connessioni, che sono soluzioni di tale equazione, formano una varietà, detta spazio dei moduli, con una ben precisa dimensione dipendente da E e da M. La topologia degli spazi dei moduli ha permesso di introdurre alcuni invarianti la cui determinazione è stata semplificata considerevolmente da idee tratte dalla fisica. Lo studio di tali invarianti su varietà di dimensione 4 ha portato alla dimostrazione di una serie di importanti teoremi che hanno evidenziato la distinzione tra varietà topologiche e varietà lisce e che sono un punto d'incontro tra la geometria differenziale, la topologia e la fisica.

Bibliografia

Atiyah 1973: Atiyah, Michael F. - Bott, Raoul - Patodi, Vijay K., On the heat equation and the index theorem, "Inventiones mathematicae", 19, 1973, pp. 279-330.

Baron 1969: Baron, Margaret E., The origins of the infinitesimal calculus, Oxford, Pergamon, 1969.

Berger, Gostiaux 1972: Berger, Marcel - Gostiaux, Bernard, Géométrie différentielle, Paris, Colin, 1972.

Besse 1987: Besse, Arthur L., Einstein manifolds, Berlin-New York, Springer, 1987.

Bianchi 1894: Bianchi, Luigi, Lezioni di geometria differenziale, Pisa, Spoeri, 1894, 3 v.

Brieskorn, Knörrer 1981: Brieskorn, Egbert - Knörrer, Horst, Ebene algebraische Kurven, Basel, Birkhäuser, 1981.

Do Carmo 1976: Do Carmo, Manfredo P., Differential geometry of curves and surfaces, Englewood Cliffs (N.J.)-London, Prentice-Hall, 1976.

Cartan 1946: Cartan, Elie J., Leçons sur la géométrie des espaces de Riemann, Paris, Gauthier-Villars, 1946.

Chern 1966: Chern, Shiing-Shen, The geometry of G-structures, "Bulletin of the American Mathematical Society", 72, 1966, pp. 167-219.

Darboux 1887-1896: Darboux, Gaston, Leçons sur la théorie générale des surfaces, Paris, Gauthier-Villars, 1887-1896.

Einstein 1916: Einstein, Alfred, Die Grundlage der allgemeinen Relativitätstheorie, ‟Annalen der Physik", 49, 1916.

Einstein 1933: Einstein, Alfred, Les fondements de la théorie de la relativité générale, Paris, Hermann, 1933 (trad. it.: La teoria della relatività, Roma, Newton, 1980).

Freed, Uhlenbeck 1984: Freed, Daniel S. - Uhlenbeck, Karen K., Instantons and four-manifolds, New York, Springer, 1984.

Goldberg 1962: Goldberg, Samuel I., Curvature and homology, New York, Academic Press, 1962.

Gray 1993: Gray, Alfred, Modern differential geometry of curves and surfaces, Boca Raton (Flo.), CRC, 1993.

Guillemin, Sternberg 1984: Guillemin, Victor - Sternberg, Shlomo, Symplectic techniques in physics, Cambridge, Cambridge University Press, 1984.

Helgason 1978: Helgason, Sigurdur, Differential geometry, Lie groups, and symmetric spaces, New York-London, Academic Press, 1978.

Hilbert, Cohn-Vossen 1932: Hilbert, David - Cohn-Vossen, Stefan, Anschauliche Geometrie, Berlin, Springer, 1932 (trad. it.: Geometria intuitiva, Torino, Boringhieri, 1960).

Hirzebruch 1966: Hirzebruch, Friedrich, Topological methods in algebraic geometry, Berlin-New York, Springer, 1966.

Hodge 1952: Hodge, William V.D., The theory and applications of harmonic integrals, Cambridge (Mass.), Cambridge University Press, 1952.

Klingenberg 1973: Klingenberg, Wilhelm, Eine Vorlesung über Differentialgeometrie, Berlin, Springer, 1973.

Kobayashi 1972: Kobayashi, Shoshichi, Transformation groups in differential geometry, Berlin, Springer, 1972.

Kobayashi, Nomizu 1972: Kobayashi, Shoshichi - Nomizu, Katsumi, Foundations of differential geometry, New York-Chichester, Interscience, 1963-1969.

McCleary 1994: McCleary, John, Geometry from a differentiable viewpoint, Cambridge, Cambridge University Press, 1994.

Milnor 1963: Milnor, John W., Morse theory. Based on lectures notes by Michael Spivak and Raymond Wells, Princeton (N.J.), Princeton University Press, 1963.

Osserman 1969: Osserman, Robert, A survey of minimal surfaces, New York 1969.

Ricci-Curbastro, Levi-Civita 1900: Ricci-Curbastro, Gregorio - Levi-Civita, Tullio, Méthodes de calcul différentielabsolu et leurs applications, "Mathematische Annalen", 54, 1900, pp. 125-201.

Spivak 1979: Spivak, Michael, A comprehensive introduction to differential geometry, 2. ed., Berkeley (Cal.), Publish or Pe-rish, 1979.

Struik 1933-1934: Struik, Dirk J., Outline of a history of differential geometry, "Isis", 19, 1933, pp. 92-120; 20, 1934, pp. 161-191.

Struik 1961: Struik, Dirk J., Lectures on classical differential geometry, Reading (Mass.), Addison-Wesley, 1961.

Thorpe 1979: Thorpe, John A., Elementary topics in differential geometry, New York, Springer, 1979.

Weil 1958: Weil, André, Introduction à l'étude des variétéskählériennes, Paris, Hermann, 1958.