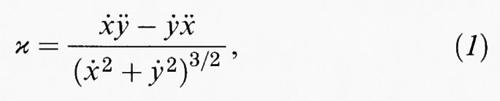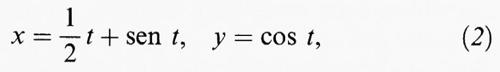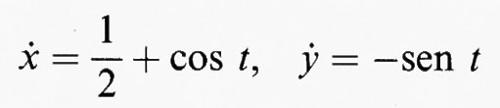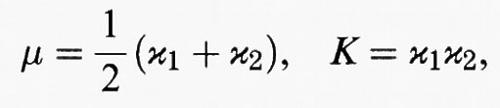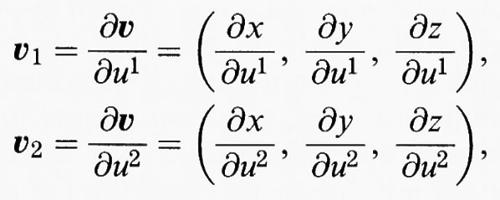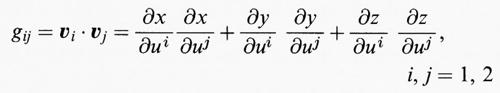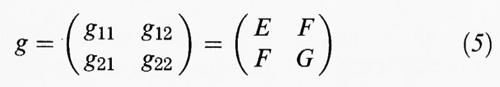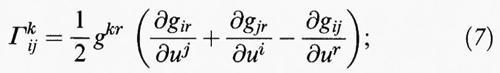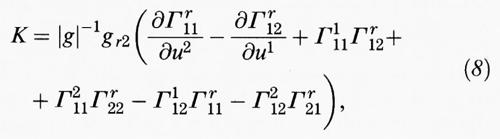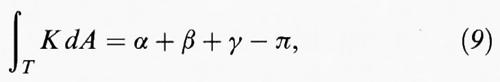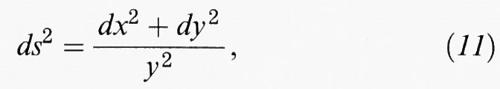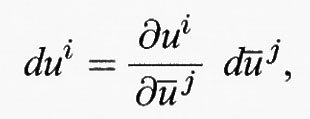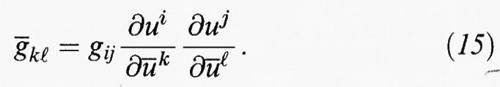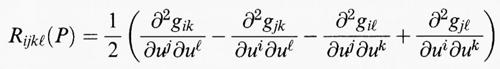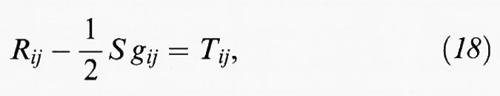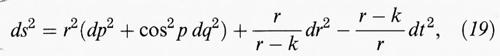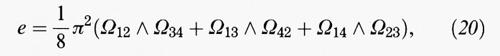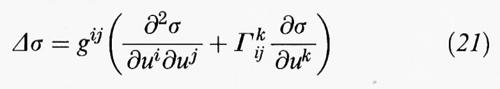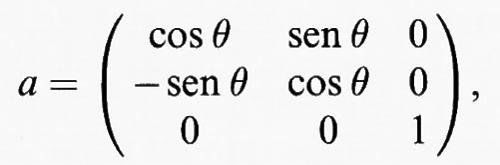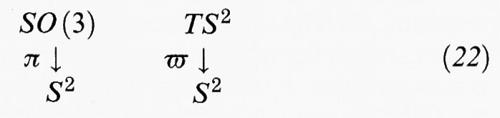Geometria differenziale

Geometria differenziale

SOMMARIO: 1. Introduzione: le origini.  2. Proprietà delle superfici.  3. Studio della curvatura gaussiana.  4. Dimensioni superiori.  5. Varietà e topologia.  6. Gruppi e fibrati.  7. Sviluppi recenti. □ Bibliografia.

1. Introduzione: le origini

La geometria differenziale è quel ramo della matematica che fa uso del calcolo differenziale e integrale per studiare e risolvere problemi che coinvolgono misure nello spazio; di conseguenza, questa materia - che ha iniziato ad assumere il suo aspetto attuale durante il XVIII secolo - risulta una combinazione di analisi e di geometria. Il concetto di ‛spazio' si è progressivamente esteso e così la geometria differenziale si è affiancata ad altri campi, quali la geometria algebrica e la topologia, per diventare uno degli argomenti centrali della matematica. Il fatto di essere attualmente un'area di ricerca molto attiva è dovuto al suo successo nella modellizzazione di vari fenomeni naturali e in particolare alla fruttuosa interazione con la fisica teorica.

Le origini della geometria differenziale si possono far risalire all'antichità, in quanto alcuni suoi concetti chiave erano noti già prima dell'invenzione dell'analisi da parte di Gottfried Leibniz e Isaac Newton alla fine del XVII secolo. Fino a quell'epoca i matematici avevano costruito solo un repertorio modesto di curve, superfici e solidi il cui studio dettagliato, tuttavia, fornì le basi di questa nuova disciplina. Problemi come la costruzione della radice cubica di 2 avevano peraltro condotto i Greci alla scoperta non solo delle coniche ma anche di altre curve piane come la cissoide e la concoide; Euclide introdusse la definizione di retta tangente a una circonferenza in un suo punto, e Apollonio, mediante la costruzione delle normali (ossia le rette perpendicolari alle tangenti) alle coniche, è quasi giunto alla nozione di curvatura, come si deduce dalle seguenti considerazioni. Dati due punti P e Q di una curva piana sufficientemente vicini, si considerino le normali alla curva in P e in Q; se il punto P rimane fisso mentre il punto Q si avvicina a P, il punto di intersezione delle due normali tende a un punto C che appartiene alla normale in P. Nel linguaggio moderno, C è detto ‛centro di curvatura' della curva nel punto P e il reciproco κ = 1/PC della distanza da P a C coincide con la curvatura in P.

Tangenti, normali e centri di curvatura sono stati trattati in un contesto più ampio solo dopo che furono saldamente stabilite le basi della geometria analitica e dopo lo studio di varie curve particolari. Il metodo delle coordinate, introdotto nel XVII secolo da Pierre de Fermat e da René Descartes, ha consentito di determinare una curva piana mediante un'equazione nelle ‛coordinate cartesiane' x e y, che rappresentano rispettivamente lo spostamento in senso orizzontale e in senso verticale da un'origine scelta, nello stesso modo in cui le indicazioni di una mappa consentono di trovare una strada in una città. Le coniche sono curve la cui equazione si ottiene annullando un polinomio di secondo grado, e per questo sono dette curve algebriche del secondo ordine; il metodo delle coordinate ha reso possibile lo studio della geometria delle curve di ordine 3 e anche di ordine superiore. Fermat, Descartes e Newton hanno contribuito alla determinazione delle curve generabili meccanicamente, come la cicloide, argomento trattato anche da Gilles Personne de Roberval e da Christian Huygens. La cicloide è la curva descritta da un punto di una circonferenza che rotola senza strisciare su una retta e la sua equazione non può essere ottenuta annullando un polinomio; Huygens è stato portato a tali ricerche dalla progettazione di un pendolo il cui periodo di oscillazione fosse indipendente dall'ampiezza dell'oscillazione stessa.

L'avvento dell'analisi è stato chiaramente anticipato dall'opera di Johannes Kepler, mentre Galileo Galilei, Bonaventura Cavalieri ed Evangelista Torricelli hanno maggiormente influenzato lo sviluppo dei metodi infinitesimali; Blaise Pascal, John Wallis, René de Sluse, Isaac Barrow e altri hanno invece individuato dei metodi geometrici atti alla determinazione delle tangenti e al calcolo di lunghezze, aree e volumi. Alla fine del XVII secolo sono stati fatti notevoli progressi su questi argomenti, soprattutto in seguito alla loro precisa formulazione, dovuta a Leibniz. L'applicazione di tali tecniche, per esempio allo studio dei punti di flesso di una curva e alle geodetiche di una superficie, è stata sviluppata in modo sistematico dai fratelli Jakob e Johann Bernoulli, che hanno in tal modo posto le fondamenta della geometria differenziale. Newton ha dimostrato che la curvatura di una curva piana di equazioni parametriche x = x (t), y = y (t) si può ottenere mediante la formula

dove il punto soprascritto indica la derivazione rispetto a t; egli ha poi applicato questo risultato agli esempi studiati da Huygens. Successivamente, uno dei più grandi successi della geometria differenziale è stata la generalizzazione del concetto di curvatura dalle curve alle superfici e quindi a spazi più astratti e a dimensioni più alte. Infatti il concetto di curvatura è così predominante che le sue conseguenze hanno condotto in modo naturale al pieno sviluppo della geometria differenziale, compreso quello avvenuto in anni recenti.

Iniziamo con una serie di commenti di tipo matematico illustrando il significato della (1). La circonferenza è un modello per la curvatura delle curve piane, essendo il luogo dei punti aventi distanza costante da un punto assegnato (il centro) che coincide anche con il centro di curvatura in ogni punto della circonferenza stessa. La curvatura κ di una circonferenza di raggio r è data da κ = 1/r, e ciò corrisponde al fatto intuitivo che più grande è il cerchio, meno curva è la sua circonferenza. Conviene pensare alla retta come a un cerchio di raggio infinito, quindi in questo contesto si può scrivere 0 = 1 / ∞ e concludere che la retta ha curvatura nulla. La curva in neretto nella fig. 1 può essere messa in relazione sia con una circonferenza sia con una cicloide: essa è un esempio di ‛trocoide', una curva che rappresenta il percorso di un punto materiale che si muove solidale e complanare con una circonferenza che rotola con velocità uniforme lungo una retta. La curva della fig. 1 è stata disegnata al computer usando il ‛comando'

che esprime le coordinate x e y in funzione del parametro t corrispondente al tempo, misurato in questo caso in radianti, come se fosse un angolo. La circonferenza si ottiene sostituendo 1/2 con zero; se invece si sostituisce 1/2 con 1 ogni cappio si riduce a un punto e la curva descritta diventa una cicloide.

La direzione della retta tangente alla trocoide in un suo punto P è determinata dalle derivate

delle equazioni (2). Il vettore (ú, ÿ rappresenta la velocità istantanea del punto in movimento e la sua derivata (ï, ÿ) = (d² x/dt₂, d₂ y/dt₂) ne individua l'accelerazione. Il punto C della fig. 1 è il centro di curvatura della curva in P e la circonferenza con centro C passante per P è il ‛cerchio osculatore': tra tutte le circonferenze con centro sulla retta normale e che incontrano la curva in P, il cerchio osculatore è quello che approssima meglio la curva in questione. Con l'aiuto del calcolo differenziale è possibile darne una definizione rigorosa in un punto qualsiasi di una curva piana arbitraria (x (t), y (t)) e dimostrare che il reciproco del suo raggio è dato dalla formula (1); pertanto, il cerchio osculatore in P ha raggio uguale all'inverso della curvatura in P. Al muoversi di P lungo la curva, il corrispondente centro di curvatura descrive una nuova curva, detta ‛evoluta' (curva a tratteggio in fig. 1). Si può anche costruire l'evoluta dell'evoluta e così via e, in molti casi, ciascuna delle evolute man mano ottenute diventa sempre più simile alla cicloide. Inoltre, l'evoluta di una cicloide è ancora una cicloide dello stesso tipo e questo - che rappresenta uno dei primi teoremi di geometria differenziale - è stato provato in modo empirico da Huygens.

2. Proprietà delle superfici

Lo studio degli oggetti in uno spazio tridimensionale ha registrato notevoli progressi nel corso del Settecento. La teoria delle curve ‛sghembe', ossia le curve per cui non esiste alcun piano che le contenga, richiede un'estensione delle tecniche precedenti che è stata introdotta da Alexis Clairaut e sviluppata parallelamente alla teoria delle superfici. Un problema importante in quest'ambito è la determinazione delle geodetiche, che sono particolari curve giacenti sulla superficie che minimizzano la distanza tra due punti sufficientemente vicini; Leonhard Euler è stato il primo a ricavarne le equazioni. Il suo lavoro sulla curvatura delle sezioni piane, vale a dire le curve intersezione della superficie con un piano, è stato approfondito da Jean Baptiste Meusnier e ha portato allo studio di alcune superfici particolari; per esempio le superfici minimali e quelle sviluppabili sono state analizzate in modo significativo rispettivamente da Joseph Louis Lagrange e da Gaspard Monge (per la loro definizione si veda la fine di questo capitolo). La determinazione delle superfici minimali è un tipico problema di calcolo delle variazioni scaturito dal lavoro dei fratelli Bernoulli sulle geodetiche e da alcuni contributi di Eulero; esso è diventato un settore specifico di ricerca in geometria differenziale per opera di Lagrange.

L'ampio lavoro di Monge ha dato un notevole impulso a molti settori della geometria. Egli infatti, forse più di ogni altro, ha iniziato a considerare i legami tra la geometria e l'analisi determinando le superfici che verificano condizioni assegnate sulla curvatura; si deve a Monge, ad esempio, la dimostrazione che le superfici sviluppabili sono generate dalle rette tangenti a una curva sghemba. Tra gli studiosi che hanno proseguito il suo lavoro, ricordiamo André-Marie Ampère, il cui nome è oggi noto non solo in quanto è usato come unità di misura dell'intensità della corrente elettrica, ma anche per le cosiddette ‛equazioni di Monge-Ampère', equazioni alle derivate parziali di importanza fondamentale nelle ricerche in quei settori costantemente in crescita che si collocano tra l'analisi e la geometria. Inoltre, rilevanti contributi alla teoria delle superfici si devono a Charles Dupin e a Olinde Rodrigues, anch'essi allievi di Monge.

Prendiamo ora in esame tutte le curve giacenti su una superficie e passanti per un suo punto generico P; è chiaro che le rette tangenti a queste curve generano il piano tangente alla superficie nel punto P, e si può definire la normale alla superficie nel punto P come l'unica retta ℓ  perpendicolare a tale piano in P. Consideriamo l'insieme dei piani passanti per ℓ  ciascuno di essi è determinato da una retta m appartenente al piano tangente in P e interseca la superficie in una curva il cui centro di curvatura C in P appartiene a ℓ. In questo modo possiamo associare a ciascuna retta m la quantità κ = 1 /PC, che può essere negativa o positiva a seconda della scelta dell'orientamento lungo ℓ  (v. fig. 2); tale corrispondenza è nota come ‛seconda forma fondamentale' della superficie in P. Eulero per primo ha dimostrato che, a meno che κ sia costante (in questo caso il punto P è detto ‛punto ombelicale', come per esempio un qualsiasi punto di una superficie sferica), i suoi valori estremi κ₁, κ₂ (scelti in modo che κ₁ 〈 κ₂) si ottengono secondo due rette perpendicolari m₁, m₂ appartenenti al piano tangente.

Per descrivere analiticamente la posizione dei punti in uno spazio tridimensionale è necessario introdurre una terza coordinata, z, che si può interpretare come l'altezza rispetto al piano su cui sono già state definite le coordinate x, y. Un'equazione in x, y, z generalmente individua una superficie, anche se è spesso più conveniente parametrizzare parte della superficie mediante una coppia ausiliare di coordinate p, q, diverse da x, y, z. La superficie della fig. 2, detta ‛toro', è descritta dalla rotazione di una circonferenza di raggio unitario intorno a una circonferenza di raggio doppio. Scegliendo un riferimento opportuno i punti del toro verificano la seguente equazione di quarto grado: 16 (x² + y²) = (x² + y² + z² + 3)²; d'altra parte, il toro può essere parametrizzato dalle equazioni:

x = (2 + cos p) cos q, y = (2 + cos p) sen q, z = sen p, (3)

dove p e q rappresentano angoli opportuni che, per analogia con la sfera, possono essere rispettivamente denominati ‛latitudine' e ‛longitudine'. Entrambe le circonferenze passanti per il punto interno P (v. fig. 2) hanno raggio 1, quindi κ₁ = - 1 e κ₂ = 1. Nel punto esterno Q le circonferenze hanno raggio 1 e 3, e pertanto, rispetto alla normale diretta verso l'interno, κ₁ = 1/3 e κ₂ = 1; poiché κ₁ e κ₂ hanno lo stesso segno la superficie in quel punto è convessa, vale a dire si dispone tutta nello stesso semispazio rispetto al piano tangente.

Carl Friedrich Gauss è considerato il ‛padre' della geometria differenziale moderna. Nella sua memoria Disquisitiones generales circa superficies curvas, del 1827 ma frutto di un lavoro di molti anni, egli ha sviluppato in modo sistematico la teoria delle ‛coordinate curvilinee' su una superficie. Infatti la notazione di Gauss

ds² = E dp² + 2 F dp dq + G dq² (4)

per la prima forma quadratica fondamentale su una superficie è tuttora comunemente usata. Questa espressione contiene implicitamente il metodo per misurare le distanze usando le coordinate p, q e generalizza la formula ds² = dx² + dy² che corrisponde al teorema di Pitagora nel piano. Per esempio, per il toro descritto in precedenza, la (4) diventa:

ds² = dp² + (2 + cos p)² dq²

che, nel caso dei punti situati nella sua parte interna vicini al cerchio minimo dato da cos p = cos (180^o) = - 1, tende alla metrica usuale del piano. Sulla superficie torica è possibile visualizzare la geometria non euclidea in cui le rette sono sostituite da geodetiche e la somma degli angoli interni di un triangolo può essere superiore o inferiore a 180°.

Più importanti di κ₁ e κ₂ sono le quantità

note come curvatura media e curvatura gaussiana, rispettivamente; esse sono inoltre funzioni definite sulla superficie, vale a dire il loro valore cambia da punto a punto. Nel caso del toro della fig. 2, μ varia da 0 (valore nel punto P, per esempio) a 2/3 (in Q) e K varia da - 1 (in P) a 1/3 (in Q). Una superficie si dice minimale se μ si annulla in ogni suo punto; in questo caso si può dimostrare che se si disegna una curva chiusa (non troppo lunga) su di essa, allora ogni perturbazione della parte di superficie interna alla curva comporta un aumento della sua area. Due delle più famose superfici minimali, il catenoide e l'elicoide, sono state scoperte da Meusnier e una parte di queste è illustrata nelle figg. 3A e 3B, rispettivamente. È noto che queste due superfici sono isometriche, vale a dire esiste un'applicazione da una all'altra che conserva le distanze, oppure in modo equivalente si possono introdurre su di esse dei sistemi di coordinate per cui le quantità E, F, G della (4) coincidono. In modo più intuitivo, ma meno preciso, si può dire che se entrambe le superfici fossero di metallo allora una potrebbe essere piegata sull'altra senza alcuna dilatazione o restringimento; il lettore può divertirsi a immaginare questo piegamento rigido che peraltro è illustrato in molti testi. Tali trasformazioni non solo conservano le distanze, ma anche il valore della curvatura gaussiana K e ciò è una conseguenza molto importante del theorema egregium di Gauss che afferma che K dipende solo da E, F, G e dalle loro derivate. Le superfici sviluppabili di Monge sono caratterizzate dall'annullarsi di K: ne sono esempi particolari il cono, il cilindro e altre superfici isometriche a regioni del piano.

3. Studio della curvatura gaussiana

Presentiamo ora una dimostrazione in termini moderni del theorema egregium di Gauss allo scopo di illustrare alcune tecniche peculiari della geometria differenziale. Per iniziare, indichiamo con u¹, u² le coordinate p, q, quindi v = (x (u¹, u²), y (u¹, u²), z (u¹, u²)) è il vettore posizione di un punto generico sulla superficie. L'introduzione di questa notazione, che può sembrare all'inizio confusa, risulta in realtà molto utile; gli esponenti 1 e 2 del simbolo u sono indici che servono a distinguere le varie coordinate. I vettori tangenti alle curve ottenute ponendo u² e u¹ costanti sono dati da:

e i prodotti scalari

individuano le lunghezze di v₁ e di v₂ e l'angolo tra di essi. Le funzioni di Gauss E, F, G coincidono rispettivamente con g₁₁, g₁₂ (e g₂₁), g₂₂ e pertanto alla (4) corrisponde la matrice

il cui determinante ∣g∣ = g₁₁ g₂₂ - g₁₂ g₂₁ = EG - F² viene usato per misurare l'area della superficie. Sia v₃ il campo vettoriale unitario normale alla superficie; allora i tre campi vettoriali v₁, v₂, v₃ costituiscono un sistema di riferimento in ogni punto (v. fig. 3A). Differenziando v₁ e v₂ si ha:

Le quantità Γⁱ_jk (ci sono 6 termini diversi in quanto per esempio Γⁱ₁₂ = Γⁱ₂₁) sono detti simboli di Christoffel, mentre gli h_ij (ce ne sono 3 diversi in quanto per esempio h₁₂ = h₂₁ danno un'espressione analitica per la seconda forma quadratica fondamentale definita nel cap. 2.

Il theorema egregium segue da due formule famose che possono essere verificate facilmente. La prima è la seguente:

essa esprime i simboli di Christoffel direttamente in funzione dei g_ij e quindi di E, F, G, e si ricava dalla (6). In questa e nelle formule successive, per alleggerire le notazioni, si applica l'usuale convenzione secondo la quale un indice ripetuto in ogni addendo (in questo caso ‛r') sostituisce una sommatoria (Σ_r). I coefficienti g^kr sono gli elementi della matrice inversa di (5) e sono dati da ∣g∣^-1 ∂ ∣g ∣/∂ g_rk. Dall'equazione K = ∣h∣/∣g∣ si deduce la seconda formula:

che fornisce la dimostrazione del teorema in quanto esprime la curvatura gaussiana mediante i simboli di Christoffel, i quali, a loro volta, sono espressi dalla (7) in funzione dei g_ij e delle loro derivate. Una scelta accurata delle coordinate può semplificare il secondo membro della (8); per esempio si ottiene che la curvatura gaussiana del toro descritto dalla (3) è cos p / (2 + cos p), da cui seguono i valori riportati nel capitolo precedente. Peraltro K è un oggetto piuttosto complicato da definire in modo astratto e la formula generale (8) non è più semplice della sua analoga in dimensione superiore.

Un aspetto fondamentale della geometria differenziale consiste nell'interazione tra le cosiddette proprietà locali e globali. La curvatura di una superficie o di una curva in un punto si può determinare esaminando soltanto una piccola regione intorno al punto, ma è chiaro che questa nozione di tipo locale può influire sull'andamento della curva o della superficie nella loro globalità. Per esempio, proprio la curvatura della sfera è responsabile della ‛sua chiusura su se stessa' e quindi del fatto che la sua area sia finita. Anche la teoria delle geodetiche mette in risalto la differenza tra locale e globale. In una regione sufficientemente piccola di una superficie, la geodetica tra due punti è l'unica curva che ne individua il percorso di minima distanza; dal punto di vista analitico, si tratta della traiettoria di una particella le cui coordinate uⁱ (t) verificano le seguenti equazioni alle derivate parziali del secondo ordine:

ü^k + Γk_ij ùⁱ ù^j = 0, k = 1, 2,

in cui i punti sopra le lettere indicano le derivate rispetto a t. Invece, se la regione considerata si ingrandisce si viene a perdere la proprietà di unicità, come nel caso della sfera, in cui le geodetiche coincidono con i cerchi massimi; lo studio di altre superfici su cui le geodetiche si richiudano su se stesse, come nel caso della sfera, rappresenta comunque un problema affascinante.

La teoria precedente è illustrata nel teorema di Gauss-Bonnet, che classicamente costituisce il punto di arrivo di molti corsi universitari di introduzione alla geometria differenziale. La sua prima formulazione, dovuta a Gauss, si applica a un ‛triangolo geodetico' inscritto in una superficie, vale a dire, una regione T delimitata da tre geodetiche. Gli angoli interni α, β, γ di T si possono misurare (in radianti) considerando le tangenti nei vertici alle curve che costituiscono i lati e si ha:

dove l'integrale a primo membro è approssimato dalla somma dei prodotti di K per l'area di regioni infinitesime. Per esempio, nel caso di una sfera di raggio r, K è uguale a 1 / r in ogni punto e il primo membro della (9) coincide con l'area del triangolo divisa per r; quindi l'area di un triangolo sferico è proporzionale alla differenza tra la somma dei suoi angoli e 180° (ossia π radianti). La formula (9) è stata generalizzata da Ossian Bonnet al caso di curve qualsiasi, non necessariamente geodetiche.

Un teorema più completo si ottiene dividendo una superficie chiusa Σ dello spazio tridimensionale in un certo numero di triangoli geodetici e sommando il contributo (9) di ciascuno di essi. Ne segue che

dove il numero χ denota la ‛caratteristica di Eulero' di Σ, pari a c₀ - c₁ + c₂, in cui c₀, c₁, c₂ rappresentano rispettivamente il numero dei vertici, dei lati e dei triangoli (le ‛facce'); indipendentemente dal modo in cui la superficie è divisa, questo numero è pari a 2 - 2 g, dove g è il numero dei ‛buchi', più propriamente detto il genere di Σ. La (10) è la più semplice di una famiglia considerevole di equazioni che mettono in relazione la curvatura di un oggetto con la sua topologia, vale a dire con la sua forma, senza alcun riferimento alla distanza, e ha applicazioni importanti. Si osservi che il primo membro della (10) non cambia quando viene variata la metrica (4); sul toro della fig. 2 i valori positivi e negativi di K si devono compensare in modo tale che si abbia χ = 0. In ogni caso, considerando il toro in modo astratto come quoziente dello spazio euclideo ℝ² (vale a dire identificando i punti le cui coordinate differiscono solo per interi), lo si può dotare di una metrica ‛piatta' per cui E = 1 = G e F = 0 in (4), in modo tale che K si annulli in ogni punto.

Esistono molte superfici a curvatura gaussiana costante negativa, che presentano quella che viene chiamata una geometria iperbolica. Ne è un esempio noto la pseudosfera formata dalla rotazione di una curva particolare, la trattrice; ma per avere una panoramica completa si devono considerare modelli più astratti, essendo la geometria iperbolica interamente caratterizzata dalla matrice (g_ij). Ponendo x = u¹ e y = u², una soluzione dell'equazione K ≡ - 1 (vale a dire K uguale a - 1 per ogni valore di x e y) è data semplicemente da g₁₁ = g₂₂ = 1/y² e g₁₂ = 0. In questo modo la (4) diventa

che è valida nel ‛semipiano superiore' formato da tutti i punti (x, y) con y positivo. In questo modello, dovuto a Henri Poincaré, le geodetiche sono archi di circonferenze con centro sull'asse orizzontale oppure rette verticali, e l'area di un triangolo iperbolico è data da π meno la somma dei suoi angoli (in radianti). La schiera infinita di ‛triangoli asintotici' indicati con a, b, c, d, ... nella fig. 4, ciascuno con tre angoli nulli, si collassa verso l'asse x; nonostante ciò l'area di ogni triangolo rimane costante e pari a π. Un risultato più profondo consiste nel fatto che ogni superficie chiusa con g ≥ 2 può essere vista come quoziente del semipiano superiore in modo da ammettere una metrica con curvatura gaussiana costante; questo è il prototipo dei teoremi di ‛uniformizzazione' in geometria differenziale.

4. Dimensioni superiori

Con la dimostrazione che la curvatura di una superficie si può calcolare direttamente in termini dei coefficienti E, F, G della prima forma quadratica fondamentale, Gauss ha introdotto la cosiddetta ‛geometria intrinseca' delle superfici, che è svincolata dalle rigide costrizioni dello spazio ambiente. Questa è una delle generalizzazioni cruciali che hanno permesso alla geometria differenziale di diventare oggi così basilare. Si deve a Bernhard Riemann il fondamentale passaggio alle dimensioni più alte, ottenuto formalizzando il concetto di tensore metrico che rende possibile definire le distanze in un modo completamente astratto: le sue idee hanno in seguito permesso di giungere al concetto di varietà noto ai giorni nostri. L'enfasi che Riemann ha posto sul ruolo svolto dalla metrica ha incrementato la validità delle geometrie non euclidee. La geometria iperbolica è parte della visione di Gauss, ma è stata chiaramente concepita da Nikolaj Lobačevskij e da János Bolyai. Si deve ad Eugenio Beltrami la dimostrazione rigorosa del fatto che questo tipo di geometria produca un sistema coerente in cui il postulato delle parallele di Euclide non vale.

Il lavoro di Riemann è stato esteso fino a giungere al ‛calcolo differenziale assoluto' da Christoffel, Gregorio Ricci-Curbastro, Luigi Bianchi e Tullio Levi-Civita. La teoria dei tensori che ne è emersa ha ricevuto un impulso enorme dalla scoperta della relatività generale dovuta ad Albert Einstein, il quale ha riconosciuto esplicitamente di dovere molto agli studi di Gauss, e si è sviluppata fino a ciò che ora si chiama ‛calcolo differenziale sulle varietà'; tuttavia, senza il linguaggio topologico necessario, l'analisi tensoriale era all'inizio totalmente dipendente dalle coordinate. Il calcolo sulle varietà si basa invece sull'equivalenza dei diversi sistemi di coordinate che rappresentano i punti su uno spazio astratto di dimensione n. Dati due tali sistemi,

(u¹, ..., uⁿ) e (ū ¹, ..., ū ⁿ), (12)

si assume che esistano n equazioni del tipo

uⁱ = uⁱ ū ¹, ..., ū ⁿ), 1 ≤ i ≤ n, (13)

che esprimono un sistema in funzione dell'altro. In questo contesto viene dato un senso agli infinitesimi, che erano in uso prima dello sviluppo del calcolo. Per esempio, l'espressione duⁱ, che prende il nome di ‛covettore' o ‛1-forma', rappresenta la velocità di cambiamento dell'i-esima coordinata uⁱ in tutti i punti possibili e in tutte le direzioni possibili e varia al variare dei sistemi di coordinate in accordo con la ‛regola della catena'

dove la sommatoria rispetto a j è implicita come nella (7).

Una metrica riemanniana è definita assegnando una matrice n × n simmetrica definita positiva (g_ij, (à_ij), ... per ogni sistema di coordinate in modo tale che

ds² = g_ij duⁱ du^j = à_ij dūⁱ dū^j = ... (14)

sia una forma quadratica invariante che è la naturale estensione della (3) a partire dalla (5). Ne segue che g_ij e à_ij sono legati dalla seguente relazione:

Questa regola di trasformazione tratta la metrica riemanniana come un tensore di tipo particolare. Si può definire la ‛lunghezza' di una curva integrando l'espressione ds = √g_ijduⁱdu^j e di conseguenza si riesce a calcolare la distanza tra due punti qualsiasi appartenenti allo spazio astratto che si sta prendendo in considerazione. L'equazione (7) ci permette di definire i simboli di Christoffel Γi_jk come nel caso delle superfici, con l'unica differenza che ora gli indici variano da 1 a n. L'analogo della (8) nel caso delle dimensioni superiori non porta a un'unica funzione scalare K, ma alle componenti R_ijkℓ  di un oggetto di grande significato e che prende il nome di ‛tensore di curvatura riemanniano'. Le funzioni R_ijkℓ si trasformano in modo analogo alla formula (15) e dato un punto P è possibile individuare un sistema di coordinate tale che il loro valore sia il seguente:

Le simmetrie che emergono da questa equazione possono essere usate per dimostrare che R_ijkℓ  (P) è determinato esattamente da n² (n² - 1)/12 numeri (quindi da un solo numero quando n = 2).

Uno dei concetti più importanti dell'analisi tensoriale, quello di connessione, era già implicito nella definizione dei simboli di Christoffel; esso fornisce un metodo per valutare la velocità con cui i vettori e i tensori variano sulla varietà; l'operatore ∇ dato da

∇ duⁱ = Γi_jk du^j du^k (16)

prende il nome di connessione di Levi-Civita. Esso viene usato per introdurre la nozione di parallelismo, che permette di stabilire quando un tensore è costante lungo una curva negli spazi considerati da Riemann. Nel caso delle superfici nello spazio tridimensionale ℝ³, la connessione di Levi-Civita coincide con la componente tangenziale della derivazione ordinaria in ℝ³ e ciò spiega la presenza dei simboli di Christoffel nella formula (6). La teoria delle connessioni è stata sviluppata da Hermann Weyl. Fu però Elie Cartan a comprenderne il significato più profondo, collocandola nell'ambito della teoria dei gruppi di Lie; egli sviluppò anche il calcolo differenziale esterno, uno strumento efficace usato ai giorni nostri per determinare le soluzioni delle equazioni differenziali geometriche.

Le teorie della relatività di Einstein si basano sul fatto che l'universo è visto come uno spazio di dimensione 4 che comprende le tre usuali coordinate spaziali x, y, z e il tempo t; il modello per la teoria della relatività speciale è lo ‛spazio piatto di Minkowski', ossia ℝ⁴ con coordinate u¹ = x, u² = y, u³ = z, u⁴ = ct (c è la velocità della luce) e tensore metrico dato da g₁₁ = g₂₂ = g₃₃ = 1 e g₄₄ = - 1. Nella teoria della relatività generale, le funzioni g_ij variano da punto a punto e la metrica si dice ‛pseudoriemanniana', in quanto la forma quadratica (14) assume anche valori negativi; infatti il percorso di un raggio di luce è una geodetica lungo la quale la ‛distanza' è nulla. Nel caso della dimensione n = 4, esattamente 10 delle 20 componenti del tensore di curvatura riemanniano possono essere ricavate dal tensore di Ricci definito nel modo seguente:

R_ij = R_ikjℓg^kℓ. (17)

È degno di nota il fatto che i tensori R_ij e g_ij siano esattamente dello stesso tipo: sono entrambi simmetrici, cioè non variano scambiando tra di loro i e j. Insieme caratterizzano le equazioni di Einstein,

dove S = R_ij g^ij è la curvatura scalare e T_ij è un tensore determinato dall'energia e dalla quantità di moto della materia nell'universo. Una delle soluzioni esplicite più semplici della (18) è la metrica di Schwarzchild,

dove r è la coordinata radiale e k è costante. La (19) modella il campo gravitazionale di una stella o di un buco nero, entrambi sfericamente simmetrici, in un universo vuoto, ossia con T_ij = 0; l'espressione tra parentesi è analoga al secondo membro della (4) e rappresenta una metrica sulla sfera. Come molte altre metriche interessanti dal punto di vista della fisica, la (19) è determinata da una matrice g diagonale (vale a dire g_ij = 0 se i ≠ j); alcuni ricercatori stanno affrontando uno studio teorico sistematico di tali metriche che comporta la definizione più rigorosa dello spazio di dimensione n concepito da Riemann.

5. Varietà e topologia

Nel corso del XX secolo, il lavoro dei geometri differenziali è progredito parallelamente alla teoria delle varietà lisce, sviluppatasi dall'idea pionieristica di Poincaré e dalle sicure fondamenta poste da H. Whitney. Successivamente, la rappresentazione della coomologia mediante forme differenziali, dovuta a G. de Rham e a W.V.D. Hodge, permise alla geometria differenziale di andare di pari passo con le più recenti idee nel campo della topologia, consentendole di ottenere alcuni dei suoi più significativi progressi.

La sfera e il toro sono esempi semplici di varietà chiuse di dimensione 2. Il termine ‛chiuso' indica che sono limitate in estensione e non hanno bordo, mentre il termine ‛varietà' indica che le regioni della superficie possono essere dotate di un sistema di coordinate e trattate come parte di un piano. Infatti, dato un punto P su una superficie in uno spazio tridimensionale, un metodo semplice per determinare le coordinate dei punti a esso vicini è quello di proiettare perpendicolarmente tali punti sul piano tangente in P, assumendo che questo si possa definire. Se però ci si allontana troppo dal punto P, due punti sulla superficie possono essere proiettati nello stesso punto sul piano e questo comprometterebbe la possibilità di dare una definizione di coordinate senza ambiguità. Di conseguenza, la superficie può essere chiamata varietà se, scegliendo regioni sufficientemente piccole intorno a diversi punti, essa può essere rappresentata da un ‛atlante' formato da una serie di ‛carte' che la ricoprono. Un controesempio semplice è dato da un doppio cono, ossia da due coni nel senso ordinario con il vertice in comune; in questo caso è chiaro che nessuna regione contenente il vertice ha la proprietà richiesta nella definizione di varietà.

Più precisamente, una varietà M di dimensione n è definita identificando o ‛incollando' regioni di ℝⁿ, spazio euclideo di dimensione n, rappresentate da sistemi diversi di coordinate come nella (12). Il concetto di varietà è così fondamentale da presentarsi in numerose branche della matematica, e i diversi tipi di varietà sono ottenuti imponendo condizioni opportune sulle funzioni che compaiono nella (13). Per gli studi di geometria differenziale si usa supporre che queste funzioni - dette ‛funzioni di transizione' - ammettano derivate parziali di ordine qualsiasi, e in questo caso la varietà si dice ‛liscia'. Le varietà lisce sono gli oggetti a cui vengono estesi in modo naturale il calcolo differenziale e integrale: l'operazione di differenziazione viene usata per definire lo spazio tangente in un punto arbitrario e la teoria delle forme esteriori permette di calcolare gli integrali sull'intera varietà come nella (10). Una varietà liscia si dice orientabile se si possono scegliere tutti i sistemi di coordinate in modo tale che il determinante di ogni matrice (∂ uⁱ/∂ ū^j) sia positivo; anche se l'orientamento è una nozione di tipo topologico, colpisce il fatto che la si possa definire così semplicemente in termini di differenziazione.

È facile considerare varietà che non si riescono a visualizzare nello spazio ordinario. Tutte le rette che passano attraverso un punto fisso O nello spazio euclideo ℝ³, di dimensione 3, possono essere pensate come punti di una varietà di dimensione 2, che prende il nome di piano proiettivo reale e che si indica come ℝP ²; è chiaro che ogni retta di questo tipo incontra una sfera S² con centro O in due punti antipodali, quindi ℝP ² si può ottenere da S² identificando punti antipodali; allora ogni regione di S² che non contenga una coppia di punti antipodali costituisce una carta di ℝP ². A differenza della sfera S², lo spazio proiettivo ℝP ² non è orientabile. Una varietà più complicata è data dall'insieme E di tutte le rette di ℝ³. Più precisamente, si può ottenere una retta generica k dalla traslazione di una retta ℓ a essa parallela e passante per O lungo una direzione perpendicolare a  ℓ, ed è perciò individuata dalla coppia (ℓ, Q), dove Q è un punto del piano ortogonale a ℓ. Tale piano può essere visto come il piano tangente a ℝP ² in ℓ, ed E risulta essere l'insieme di tutti i punti di questi piani tangenti, al variare di ℓ in ℝP²; E prende il nome di fibrato tangente di ℝP² ed è una varietà di dimensione 4.

Una varietà liscia si dice riemanniana se è dotata di una metrica definita in termini delle coordinate come nella (14). Nell'ipotesi in cui M sia una varietà riemanniana chiusa di dimensione n, si perviene ad alcune generalizzazioni del teorema di Gauss-Bonnet (10). Dal punto di vista puramente topologico, una varietà può essere sempre costruita in vari modi mediante una collezione di ‛celle' di dimensioni diverse. Per esempio, un ‛ipercubo' di ℝ⁴ può essere visto come una varietà topologica di dimensione 3 (si richiede solo che le funzioni di transizione siano continue) con 16 vertici, 32 spigoli, 24 facce e 8 celle di dimensione 3. Allora la definizione di caratteristica di Eulero si può estendere ponendo χ = Σn_p=0 (- 1)^p c_p, dove c_p è il numero delle celle di dimensione p; quindi nel caso dell'ipercubo suddetto si ha c₀ = 16, c₁ = 32, c₂ = 24, c₃ = 8, e pertanto χ = 0, il che è in realtà vero per ogni varietà orientata di dimensione dispari. Infatti χ risulta essere anche uguale a Σn_p=0 (- 1)^p b_p, dove i b_p sono i numeri di Betti - così chiamati da Poincaré in onore di Enrico Betti - che, a differenza dei c_p, dipendono solo dalla topologia della varietà. Un teorema di S.-S. Chern esprime χ nel caso generale come integrale di una quantità e definita tramite il tensore di curvatura; per esempio, nel caso della dimensione 4, è data da:

dove Ω_ij = R_ijkℓ du^k ⋀ du^ℓ. L'espressione du^k ⋀ du^ℓ può essere considerata un'abbreviazione del prodotto antisimmetrico du^k du^ℓ- du^ℓdu^k ed è una 2-forma definita nel sistema di coordinate considerato. Viceversa, la legge di trasformazione tensoriale valida per R_ijkℓ fa sì che e sia una 4-forma definita globalmente, vale a dire per tutti i punti della varietà M e, di conseguenza, la rende una quantità che può essere integrata su M.

I numeri di Betti sulla varietà M si calcolano, a partire dai teoremi di de Rham e di Hodge, usando le forme differenziali. Infatti, b_p coincide con la dimensione dello spazio delle forme armoniche, vale a dire delle soluzioni dell'equazione Δ σ = 0, dove σ è una p-forma e Δ è una generalizzazione dell'operatore di Laplace. Per p = 0, σ è una funzione ordinaria e la definizione

coinvolge la connessione di Levi-Civita definita nella (16). Il secondo membro della (21) non dipende dalla scelta delle coordinate, e ciò mostra come si possano introdurre in modo naturale gli operatori differenziali sulle varietà. Nel caso in cui M sia chiusa, connessa e orientata, b₀ e b_n sono entrambi uguali a 1; più in generale, b_p = b_n-p, da cui segue subito che se n è dispari allora χ = 0. Tenendo conto che ogni forma armonica è un autovettore di Δ con autovalore nullo, l'insieme di tutti gli autovalori (cioè i numeri λ per cui esistono soluzioni dell'equazione Δσ=λσ) prende il nome di ‛spettro' di M. Il modo in cui una metrica riemanniana è determinata dal suo spettro costituisce un problema molto importante a cui ci si riferisce con la famosa domanda di M. Kac: ‛si può sentire la forma di una varietà?'.

L'equazione Δ σ = 0 per una p-forma con p ≥ 1 equivale alla coppia di equazioni differenziali del primo ordine dσ = 0 e d*σ = 0, dove d e d* sono particolari operatori che nel caso p = 1 generalizzano rispettivamente i ben noti ‛rotore' e ‛divergenza' dell'analisi vettoriale; d è la differenziazione esterna e, a differenza di d*, può essere definita indipendentemente dalla metrica. Nonostante ciò, l'operatore differenziale ora considerato essenziale è quello di Dirac, che si definisce tramite la teoria delle algebre di Clifford e dal quale possono essere dedotti d, d* e tanti altri operatori differenziali. Gli spazi delle soluzioni delle equazioni differenziali che ne seguono dipendono, in generale, dalla scelta della metrica riemanniana, anche se le loro dimensioni determinano degli interi, detti ‛indici', che sono analoghi alla caratteristica di Eulero e si possono esprimere tramite quantità puramente topologiche usando il teorema dell'indice di M. F. Atiyah e I. M. Singer.

La teoria delle forme armoniche, rilevante per il lavoro di K. Kodaira che caratterizza le varietà proiettive in geometria algebrica, è stata applicata da A. Weil e da altri allo studio delle varietà kähleriane (v. cap. 7) ed è anche da mettersi in relazione con la teoria dei punti critici delle funzioni lisce introdotta da M. Morse estendendo il lavoro di H. Hopf. Questi due settori hanno dato luogo rispettivamente alle teorie moderne di Hodge e di Morse e costituiscono una delle applicazioni più importanti dell'analisi alla topologia; i loro sviluppi recenti formano una parte importante della matematica contemporanea.

6. Gruppi e fibrati

La geometria, secondo la definizione di Felix Klein, consiste nello studio degli oggetti che non variano quando ad essi vengono applicati gruppi particolari di trasformazioni. Tali gruppi e i loro corrispettivi infinitesimi sono stati studiati intensamente da Sophus Lie e da Wilhelm Killing e applicati a problemi geometrici da Luigi Bianchi e da Gaston Darboux - autori, rispettivamente, di Lezioni di geometria differenziale e Leçons sur la théorie générale des surfaces, che sono considerati due testi chiave. All'epoca della loro pubblicazione, alla fine dell'Ottocento, sono stati compiuti molti sforzi per cercare di mettere in relazione le strutture geometriche più rigide definite dai gruppi di Lie e il tipico apparato riemanniano in cui le strutture locali variano da punto a punto. L'abbandono del concetto di distanza come nozione fondamentale conduce alla teoria delle connessioni, anche se tutto ciò non è giunto a completa maturazione fino all'introduzione della nozione di fibrato, che costituisce la naturale estensione della nozione di varietà. Le connessioni sono state incorporate in questo quadro generale da C. Ehresmann, e successivamente sono state impiegate per definire le classi caratteristiche, di cui la (21) costituisce un esempio.

La sfera, il piano euclideo e il semipiano superiore (introdotto in precedenza; v. cap. 3) sono modelli di superfici con curvatura gaussiana costante. Ci sono modi diversi di interpretare il concetto di curvatura costante in dimensioni superiori e ciò ha fatto scaturire un'intera serie di problemi interessanti. Innanzitutto si potrebbe richiedere che il tensore di curvatura non cambi da punto a punto; tale proprietà si verificherebbe, per esempio, se per ogni coppia di punti P, Q sulla varietà esistesse una trasformazione che mandi P in Q e che conservi le distanze, vale a dire un'isometria. Nell'ambito della geometria riemanniana le varietà che ammettono tali isometrie prendono il nome di spazi omogenei e molti risultati sono più facili da capire nel caso omogeneo; per esempio, vi sono varietà che pur non essendo omogenee sono costruite in modo semplice a partire dagli spazi omogenei; è stata inoltre sviluppata una teoria molto ricca sulle metriche di Einstein e sull'operatore di Dirac, sullo spazio totale dei fibrati vettoriali su spazi omogenei. In questo capitolo presenteremo uno degli esempi più semplici di fibrato, un concetto che ha un ruolo fondamentale in gran parte delle ricerche attuali.

Uno degli spazi omogenei più facili da descrivere è la sfera ordinaria S², luogo dei punti dello spazio euclideo ℝ³, di dimensione 3, aventi distanza unitaria dall'origine. Ogni rotazione di ℝ³ intorno all'origine è un'isometria che può far corrispondere due punti qualsiasi della sfera. Siano P₁, P₂, P₃ i punti della sfera S² rispettivamente di coordinate (1, 0, 0), (0, 1, 0), (0, 0, 1), posti sugli assi cartesiani. Ogni rotazione può essere rappresentata da una matrice quadrata di ordine 3,

in cui le righe esprimono nell'ordine le coordinate dei punti immagine, mediante a, di P₁, P₂, P₃; per esempio (a₃₁, a₃₂, a₃₃) = (0, 0, 1) a in accordo con la regola del prodotto di matrici. Ne segue che le righe di a formano una base ortonormale di vettori per ℝ³ (vale a dire sono vettori unitari a due a due ortogonali) e il determinante di a è uguale a 1. L'insieme delle rotazioni di ℝ³ intorno all'origine, che normalmente si indica con SO (3), è un gruppo di Lie, ossia ha la struttura di varietà liscia compatibile con la legge del prodotto di due matrici, dove per ‛prodotto' ab di due rotazioni si intende la rotazione in cui a è seguita da b. Le rotazioni intorno all'asse passante per l'origine e per il ‛polo nord' P₃ sono del tipo

e formano un sottogruppo H di SO (3), che rappresenta quindi il gruppo delle rotazioni (con angolo θ variabile) del piano equatoriale. Data una matrice b di SO (3), le rotazioni aventi la stessa terza riga di b sono esattamente quelle della forma ab con a in H; queste formano ciò che si chiama un ‛laterale' e che si scrive in modo naturale come Hb. Tale situazione si descrive schematicamente mediante il primo dei due diagrammi seguenti:

in cui π indica l'applicazione che associa a ogni matrice b la sua terza riga. Ogni laterale è quindi la controimmagine π^-1 (Q) di un punto Q qualsiasi della sfera (la notazione π^-1 (Q) indica tutte le matrici b che π manda in Q) e coincide con una circonferenza. Dato Q, una matrice b di π^-1 (Q) è determinata dalle sue prime due righe, che rappresentano le immagini di P₁, P₂ mediante b. Se identifichiamo P₁, P₂ con i vettori tangenti alla sfera in P₃ otteniamo che ogni matrice b in SO (3) è data semplicemente da una coppia ortonormale di vettori tangenti a S² nel punto π(b).

L'applicazione π permette di rappresentare SO (3) come un fibrato sulla sfera le cui fibre sono le controimmagini π^-1 (Q) al variare di Q. Più precisamente, un fibrato è determinato da tre varietà E, F e M e da una applicazione π : E → M definita in modo che ogni punto Q di M appartenga a una regione U tale che π^-1 (U) si possa identificare con il prodotto U × F; in altri termini, lo spazio totale E è localmente il prodotto di F con la base M. Infatti il primo diagramma della (22) prende il nome di fibrato principale in quanto ogni fibra può essere vista come la copia di un gruppo (in questo caso H). Un altro esempio di fibrato, ma di tipo diverso dal precedente è il fibrato tangente a S² rappresentato dal secondo diagramma della (22), in cui la fibra 6^-1 (Q) è lo spazio tangente a S² in Q o, in modo equivalente, il complemento ortogonale Q^⊥ di Q in ℝ³. Si tratta in questo caso di un fibrato vettoriale di rango 2, poiché F è uno spazio vettoriale di dimensione 2. I due fibrati della (22) sono fortemente collegati, dato che ogni fibra del fibrato principale è costituita dalle basi ortonormali della fibra corrispondente del fibrato vettoriale. Più generalmente, su ogni varietà liscia M può essere definito in modo astratto lo spazio tangente in ogni punto e quindi il fibrato tangente TM, mentre la scelta di un fibrato principale opportuno dipende dalla struttura che si sta considerando.

Il gruppo SO (3) appartiene a una delle tre famiglie di gruppi di Lie compatti, di tipo particolare e di notevole importanza, denominate SO (n), SU (n) e Sp (n). Infatti, ciascuna di queste è un insieme di matrici che verificano ben determinate equazioni e ha la struttura di varietà liscia di dimensione (n² - n)/2, n² - 1, 2 n² + n, rispettivamente. Per completare la lista di questo tipo di gruppi se ne devono aggiungere altri cinque, detti eccezionali: G₂, F₄, E₆, E₇, E₈P, che hanno rispettivamente dimensione 14, 52, 78, 133, 248. Dato un sottogruppo chiuso H di un gruppo di Lie G, l'insieme dei laterali G/H risulta essere la base di un fibrato principale con fibra H e spazio totale G. Ogni spazio omogeneo è del tipo G/H e scelte particolari di G e di H definiscono i cosiddetti spazi simmetrici, classificati da Cartan, il cui tensore di curvatura è costante rispetto alla connessione di Levi-Civita. Per esempio, gli spazi omogenei SO (8)/SO (7), SU (4)/SU (3), Sp (2)/Sp (1) sono tutti equivalenti alla sfera S⁷ di dimensione 7, come varietà liscia, ma solo il primo ammette una metrica riemanniana ben precisa che lo colloca nella lista di Cartan. Più generalmente, dato K sottogruppo di H, che è a sua volta un sottogruppo di G, si può costruire il fibrato con E = G/K, F = H/K e M = G/H; lo studio di tali fibrati ha condotto a rilevanti risultanti nel caso particolare in cui la base M sia uno spazio simmetrico, poiché lo spazio totale E risulta avere uno spettro di strutture geometriche più ampio di quello di M.

7. Sviluppi recenti

Fin dalla scoperta del teorema di Gauss-Bonnet (10), l'interazione tra curvatura e topologia è stata oggetto di studio continuo. È tipico chiedersi se una varietà chiusa possa o meno ammettere una metrica riemanniana con tensore di curvatura assegnato; in tale contesto ci si può anche riferire alla curvatura di Ricci R_ij e alla curvatura scalare S definite nel cap. 4. Teoremi di questo tipo, dovuti a S. B. Myers e a S. Bochner, affermano che, se il tensore di Ricci è positivo nello stesso modo in cui assumiamo che lo sia la metrica (14), allora la varietà è necessariamente chiusa e il suo primo numero di Betti b₁ si annulla. Per quanto riguarda la curvatura scalare, il cosiddetto ‛problema di Yamabe' (la cui soluzione è stata completata recentemente da R. Schoen) consiste nel provare che ogni metrica riemanniana su una varietà chiusa può essere moltiplicata per una funzione positiva in modo da ottenere una metrica la cui curvatura scalare sia costante. D'altra parte, è noto che vi sono ostruzioni all'esistenza di metriche con curvatura scalare positiva emerse dallo studio delle soluzioni dell'operatore di Dirac su particolari fibrati.

Riveste un interesse particolare, sia per i matematici sia per i fisici, la classificazione delle varietà riemanniane, dette di Einstein, il cui tensore di Ricci verifica un'equazione analoga alla (18) con T_ij identicamente nullo. Mentre questo discorso è relativamente facile in dimensione 2 e 3, non è neppure noto se le uniche varietà di dimensione 4 chiuse con tensore di Ricci nullo siano solo i due esempi che derivano dalla geometria complessa e di cui parleremo più avanti. La curvatura delle varietà riemanniane di dimensione 4 è particolarmente interessante per il fenomeno dell'autodualità che divide in due parti la metà del tensore R_ijkℓ complementare al tensore di Ricci. La ‛teoria dei twistors', introdotta da R. Penrose, fa sì che metriche speciali possano essere costruite usando tecniche proprie della teoria delle funzioni complesse. In dimensioni superiori un problema più trattabile è quello della classificazione delle metriche di Einstein sugli spazi omogenei; attualmente, invece, l'attenzione è rivolta allo studio del caso più generale dei biquozienti FG/H, che sono varietà definite tramite laterali doppi determinati da due sottogruppi F, H di un gruppo di Lie G. Il caso particolare in cui F sia finito e G/H uno spazio simmetrico consiste nel problema degli ‛space forms generalizzati' affrontato da J. A. Wolf. In questo momento alcune ricerche sono incanalate verso esempi molto speciali di metriche di Einstein, le cosiddette metriche con olonomia eccezionale, la cui esistenza è stata ipotizzata da M. Berger nel 1955.

Ricordiamo che una metrica riemanniana è un tensore, che indicheremo semplicemente con g, individuato da una forma bilineare simmetrica definita positiva su ogni spazio tangente. Mentre si può pensare che la geometria riemanniana rimanga il ramo più importante della geometria differenziale, negli ultimi tempi si sono studiate altre classi di varietà definite da tensori analoghi a g. Tra queste ricordiamo le varietà quasi simplettiche, determinate da una forma bilineare ω antisimmetrica non degenere su ogni spazio tangente, e le varietà quasi complesse, definite da un isomorfismo J su ogni spazio tangente che mimi la moltiplicazione per i = √-1 dei numeri complessi. Entrambe queste classi di varietà devono essere di dimensione pari e il prefisso ‛quasi' si toglie se esistono coordinate compatibili con ω e con J. Ne segue che una varietà simplettica di dimensione 2n è caratterizzata dall'esistenza di una 2-forma ω per cui ωⁿ è non nulla in ogni punto e d ω = 0. Tali varietà si presentano in modo naturale come spazio delle configurazioni dei sistemi meccanici e sono spesso associate all'azione di gruppi di Lie. Nello stesso spirito, una varietà complessa di dimensione reale 2n è caratterizzata dall'esistenza di sistemi di n coordinate come nella (12) che sono a valori complessi e le cui funzioni di transizione come nella (13) sono analitiche complesse.

Ogni superficie orientata Σ di ℝ³ è una varietà kähleriana, vale a dire una varietà che è contemporaneamente riemanniana, complessa e simplettica, con g, ω, J compatibili in modo opportuno. Il tensore J è definito su Σ mediante la rotazione di 90° dei vettori di ogni spazio tangente, dopo aver deciso se scegliere l'andamento orario o quello antiorario. Tutto ciò è legato a un teorema ben noto, in cui si afferma che è sempre possibile determinare, in un intorno di ogni punto di M, un sistema di coordinate x = u¹, y = u² in modo tale che g₁₁ = g₂₂ e g₁₂ = 0, da cui

ds² = E (dx² + dy²)

come nella (11); la funzione z = x + iy funge allora da coordinata complessa su Σ. Esempi significativi di varietà kähleriane di dimensione superiore a 2 sono dati dalle sottovarietà dello spazio proiettivo complesso ℂPⁿ, il cui studio costituisce una buona parte della geometria algebrica. La dimostrazione di S.-T. Yau di una congettura di E. Calabi determina l'esistenza di una grande famiglia di varietà kähleriane chiuse con tensore di Ricci nullo. In dimensione 4 ciascuno di questi spazi equivale, come varietà liscia, al toro di dimensione 4 (il prodotto del toro di dimensione 2 della fig. 2 con se stesso) oppure alla superficie K3, una particolare varietà con caratteristica di Eulero χ = 24. Nessun risultato di questo tipo, ossia di classificazione generale, è attualmente noto per gli spazi di Calabi-Yau di dimensione 6; si tratta di un argomento intensamente studiato dai fisici teorici nel quale si ritrova l'interessante fenomeno della ‛simmetria speculare', da cui emergono (almeno a livello sperimentale) coppie di varietà correlate topologicamente in qualche modo. La superficie K3 appartiene anche a un'altra classe ristretta di varietà kähleriane, le cosiddette varietà iperkähleriane, che ammettono alcune strutture kähleriane compatibili con una metrica fissata. La dimensione di una varietà iperkähleriana è sempre 4 m con m intero e il prodotto mχ è divisibile per 24.

La teoria delle varietà simplettiche e complesse, considerata come argomento a sé stante, è molto diversa dalla teoria delle varietà riemanniane; non esistono infatti concetti analoghi a quello del tensore di curvatura e quindi è necessario imporre strutture addizionali per poterne studiare la conformazione. Di conseguenza, è difficile determinare se e quando una data varietà liscia possa essere dotata di un tensore ω e/o J in modo da diventare simplettica e/o complessa; devono essere soddisfatte innanzi tutto alcune condizioni topologiche: per esempio, ogni varietà simplettica chiusa deve avere b₂ ≠ 0. D'altra parte in dimensione uguale o superiore a 6 non si conoscono esempi di varietà quasi complesse che non possano essere complesse; un candidato è la sfera S⁶ di dimensione 6, ma non si è ancora in possesso delle tecniche adatte a determinare l'esistenza o meno di una struttura complessa su di essa. Questo tipo di problemi appartiene più propriamente ai campi della topologia differenziale e dell'analisi globale, ma l'uso di metodi tipici della geometria differenziale ha permesso di compiere notevoli progressi nel loro studio. Per esempio, un teorema recente, dimostrato da C. H. Taubes, afferma che ogni forma simplettica sul piano proiettivo complesso ℂP² è equivalente a quella determinata dalla struttura kähleriana standard. Tale teorema è stato ottenuto combinando alcuni risultati di M. Gromov sulle sottovarietà simplettiche insieme con la ‛teoria di gauge'.

Si sono avuti progressi fondamentali nel caso delle varietà lisce di dimensione 4 grazie alla formulazione matematica - da parte di S. K. Donaldson, A. Floer, E. Witten e altri - della teoria di gauge, introdotta dai fisici negli anni sessanta. La controparte matematica di un campo di gauge è il tensore di curvatura di una connessione, o potenziale di gauge, definito su un fibrato particolare su una varietà M le cui fibre possono essere delle circonferenze, come descritto nel capitolo precedente. Le connessioni sono studiate in relazione alla geometria dello spazio totale E del fibrato e, nel caso della dimensione 4, si ottengono in modo naturale in termini di un'equazione differenziale non lineare del primo ordine imponendo una condizione sulla curvatura. Con appropriate ipotesi, le classi di equivalenza delle connessioni, che sono soluzioni di tale equazione, formano una varietà, detta spazio dei moduli, con una ben precisa dimensione che dipende da E e da M. La topologia degli spazi dei moduli ha permesso di introdurre alcuni invarianti la cui determinazione è stata semplificata considerevolmente da idee tratte dalla fisica. Lo studio di tali invarianti su varietà di dimensione 4 ha portato alla dimostrazione di una serie di importanti teoremi che hanno evidenziato la distinzione tra varietà topologiche e varietà lisce e che sono un punto d'incontro tra la geometria differenziale, la topologia e la fisica.

Prima di concludere, vogliamo fare un'ultima considerazione. La geometria differenziale è uno dei principali beneficiari delle tecniche di visualizzazione tramite computer (ad esempio, le figure di questo articolo sono state agevolmente disegnate utilizzando il programma Mathematica) che ora riescono a far apprezzare alcuni tra i problemi più difficili anche agli studenti e agli aspiranti ricercatori, il che a sua volta facilita i progressi delle aree di studio e di ricerca tradizionali. Un esempio importante è dato dalla classificazione delle superfici minimali e di altre superfici che verificano particolari condizioni per la curvatura. Lo studio delle varietà ha ampliato la formulazione del classico problema di Plateau, che consiste nel dimostrare l'esistenza di una superficie minimale delimitata da una curva chiusa assegnata (ad esempio, un anello di fil di ferro immerso in acqua saponata); sono state risolte anche alcune versioni moderne dello stesso problema riguardanti sottovarietà minimali senza bordo in dimensioni superiori. Ciò può essere visto come un'estensione dello studio delle geodetiche, che sono ‛curve minimali' la cui conformazione dà inoltre preziose informazioni non solo sulla struttura delle varietà, ma anche sul percorso dei raggi di luce nel modello spazio-tempo descritto nella (19); non si deve però dimenticare che questi argomenti scaturiscono naturalmente dal campo classico del calcolo delle variazioni di Eulero e di Lagrange.

BIBLIOGRAFIA

Baron, M. E., The origins of the infinitesimal calculus, Oxford 1969.

Berger, M., Gostiaux, B., Géométrie différentielle, Paris 1972.

Besse, A. L., Einstein manifolds, Berlin-New York 1987.

Brieskorn, E., Knörrer, H., Ebene algebraische Kurven, Basel 1981.

Carmo, M. P. do., Differential geometry of curves and surfaces, Englewood Cliffs, N. J., 1976.

Einstein, A., Théorie de la relativité, Paris 1921 (tr. it.: La teoria della relatività, Roma 1980).

Freed, D. S., Uhlenbeck, K. K., Instantons and four-manifolds, New York 1984.

Goldberg, S. I., Curvature and homology, New York 1962.

Gray, A., Modern differential geometry of curves and surfaces, Boca Raton, Flo., 1993.

Guillemin, V., Sternberg, S., Symplectic techniques in physics, Cambridge 1984.

Helgason, S., Differential geometry, Lie groups, and symmetric spaces, New York 1978.

Hilbert, D., Cohn-Vóssen, S., Anschauliche Geometrie, Berlin 1932 (tr. it.: Geometria intuitiva, Torino 1960).

Kline, M., Mathematical thought from ancient to modern times, New York 1972 (tr. it.: Storia del pensiero matematico, 2 voll., Torino 1991).

Klingenberg, W., Eine Vorlesung über Differentialgeometrie, Berlin 1973.

Kobayashi, S., Nomizu, K., Foundations of differential geometry, 2 voll., New York 1963-1969.

McGeary, J., Geometry from a differentiable viewpoint, Cambridge 1994.

Milnor, J. W., Morse theory. Based on lectures notes by M. Spivak and R. Wells, Princeton, N. J., 1963.

Mishchenko, A. S., Fomenko, A. T., Kurs differentsial'noi geometrii i topologii, Moskva 1980 (ed. ingl. aggiornata: A course of differential geometry and topology, Moscow 1988).

O'Neill, B., Semi-Riemannian geometry: with applications to relativity, New York 1983.

Osserman, R., A survey of minimal surfaces, New York 1969.

Spivak, M., A comprehensive introduction to differential geometry, 5 voll., Berkeley, Cal., 1979².

Struik, D. J., Outline of a history of differential geometry, in ‟Isis", 1933, XIX, pp. 92-120 e XX, pp. 161-191.

Struik, D. J., Lectures on classical differential geometry, Reading, Mass., 1961².

Thorpe, J. A., Elementary topics in differential geometry, New York 1979.