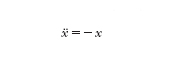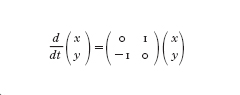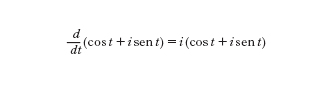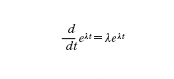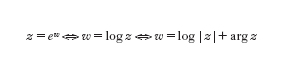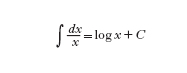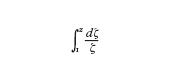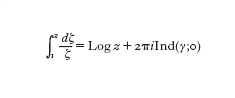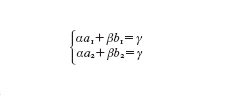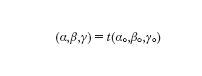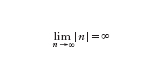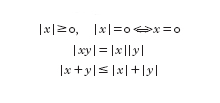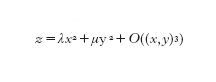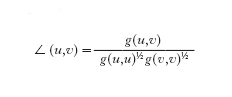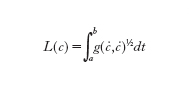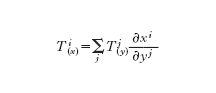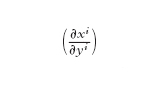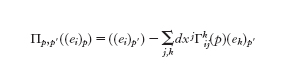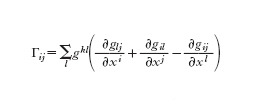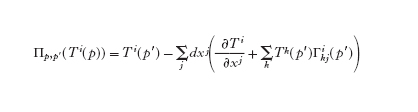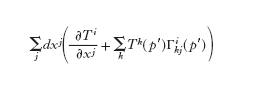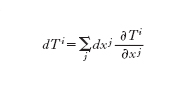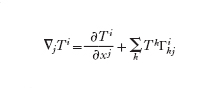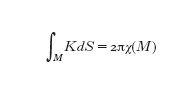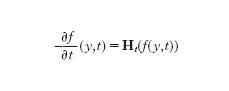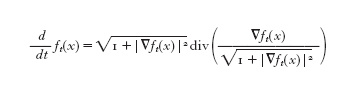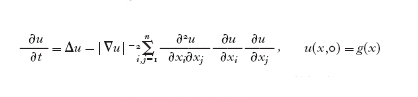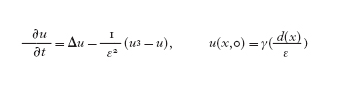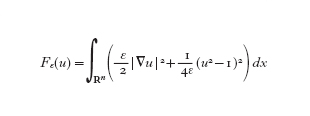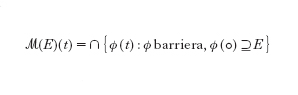Geometria

Geometria

(XVI, p. 623; App. III, i, p. 724; IV, ii, p. 39; V, ii, p. 391)

Numerose voci dell'Enciclopedia Italiana trattano i vari oggetti e metodi geometrici, fra cui analitica, geometria (p. 86) nel vol. III; coniche (p. 151), coordinate (p. 294), e continuità (p. 237) nel vol. XI; cubiche (p. 67), curvatura (p. 171), curve (p. 172), descrittiva, geometria (p. 667) e dimensioni (p. 849) nel vol. XII; dualità (p. 232) nel vol. XIII; iperspazio (p. 473) nel vol. XIX; superficie (p. 1) nel vol. XXXIII. Nella voce geometria viene presentata, da una prospettiva storica, una panoramica della g. classica, dalle sue origini in Grecia fino agli indirizzi geometrici più moderni, con particolare riguardo per la g. proiettiva, considerati secondo la classificazione proposta da F. Klein alla fine dell'Ottocento attraverso il concetto di gruppo applicato alle trasformazioni geometriche; si considera inoltre rilevante il problema del significato fisico della g. e il legame fra gli sviluppi matematici e le feconde discussioni sul problema dello spazio nei primi decenni del 20° secolo.

Le Appendici registrano l'evoluzione, per certi versi paradossale, delle discipline geometriche a partire dagli anni Trenta. La tendenza verso l'algebrizzazione sotto l'influsso del metodo assiomatico in matematica ha portato a un grande sviluppo della g. algebrica secondo un approccio molto astratto, che si discosta da quello della scuola italiana e che allontana il pensiero geometrico dalle basi empirico-intuitive e dal problema generale dello spazio. L'interazione fra la g. e altri settori della matematica viene vista come una fusione nella quale non è più possibile riconoscere la g. tradizionale, anche se l'importanza della visione geometrica dei problemi viene riaffermata, soprattutto negli ultimi decenni del 20° secolo. Di conseguenza, nelle App. III, IV e V la voce geometria è dedicata quasi interamente alla g. algebrica; sotto altri lemmi dedicati all'analisi matematica o alla topologia si ritrovano invece gli sviluppi della g. differenziale e altri temi geometrici come i frattali o l'analisi qualitativa delle equazioni differenziali (v. equazioni, App. IV, i, p. 714; equazioni differenziali, App. V, ii, p. 131; funzionale, analisi, App. V, ii, p. 344; topologia, App. V, v, p. 512; varietà, App. IV, iii, p. 795; tensoriale, algebra e analisi, App. IV, iii, p. 612; frattali, App. V, ii, p. 329; stringa, App. V, v, p. 307). Alcuni studi recenti permettono di illustrare la situazione attuale delle ricerche, il collegamento di esse con i problemi classici e il continuo e fecondo rapporto fra fisica e geometria. *

L'approccio geometrico in matematica

di Ryoichi Kobayashi

La matematica, e in particolare il pensiero geometrico, contribuisce al tentativo delle scienze di individuare le componenti fondamentali dei fenomeni naturali e osservare le relazioni mutue tra di esse. Queste componenti costitutive sono, in linea di principio, indipendenti dai fenomeni che vengono osservati nel mondo reale: vale a dire, ciò che può essere osservato in realtà è, al massimo, una qualche specie di approssimazione di tali componenti costitutive. Un semplice esempio di tale situazione è dato dal moto di un pendolo ideale. Il termine 'ideale' significa che l'ampiezza di oscillazione è 'idealmente' piccolo rispetto alla lunghezza del pendolo. La comprensione matematica di questa situazione (che fornisce un buon esempio degli aspetti teorici contenuti anche nella matematica a livello scolastico) chiarisce meglio che cosa sia l'approccio geometrico. Secondo la suddetta idealizzazione, la seconda legge di Newton ci dice che il moto del pendolo ideale è descritto essenzialmente tramite l'equazione differenziale (per pulsazione unitaria):

[1] formula

La soluzione di questa equazione è x=Acost+Bsent, dove A e B sono costanti determinate dallo stato iniziale del pendolo (v. equazioni).

Tuttavia, da un punto di vista geometrico lo scopo non è quello di risolvere l'equazione [1] bensì quello di provare a comprendere i concetti che stanno dietro l'equazione [1]. Il moto del pendolo ideale è un moto periodico di un punto sull'asse reale. Supponiamo che si voglia conoscere lo stato del punto al tempo t: tale stato è dato dalla posizione e dalla velocità. In tal caso è chiaro che la retta reale non è sufficiente per conoscere lo stato del punto: nella retta possiamo rappresentare soltanto la posizione, la quale non è sufficiente per descrivere completamente il moto del pendolo ideale. È necessario introdurre una nuova dimensione che descriva la velocità del punto. Matematicamente questo processo avviene combinando in forma matriciale l'equazione [1] e l'equazione ottenuta differenziando la [1] (dove si pone y=x.):

[2] formula.

È possibile fornire una rappresentazione geometrica dell'equazione differenziale [2]. Infatti tale equazione ha un chiaro significato geometrico: il vettore velocità del punto (x,y) al tempo t non è altro che il vettore ottenuto ruotando (x,y) di un angolo −π/2 (l'angolo retto in direzione oraria). Se si rappresenta graficamente il campo vettoriale associato all'equazione differenziale [2] si ottiene una figura simmetrica rispetto al gruppo delle rotazioni intorno all'origine. Le traiettorie determinate dal campo vettoriale sono tutte circonferenze centrate nell'origine e il punto che rappresenta lo stato del pendolo ruota lungo una di tali circonferenze con periodo 2π. In questo modo si ottiene una comprensione completa del moto del pendolo ideale, poiché, a partire dalla suddetta rappresentazione, si conosce lo stato completo del punto (la componente x è la posizione e la componente y è la velocità). Un altro evidente vantaggio del punto di vista geometrico è dato dalla chiara rappresentazione della costante del moto: il raggio del cerchio è costante durante tutto il moto e questo rappresenta la legge di conservazione dell'energia. Si tratta del più semplice esempio di spazio delle fasi in meccanica analitica, nozione che è stata all'origine della moderna g. in dimensione superiore.

Si considerino ora i numeri immaginari. La seguente relazione descrive il moto periodico con velocità costante di un punto che si muova lungo una delle traiettore prima descritte:

.

Tenendo presente la ben nota formula

si pone e^it=cost+isent e si arriva quindi alla definizione della funzione esponenziale complessa e^z:=e^Rez (cosImz+isenImz), dove indichiamo con Rez la parte reale di z e con Imz la parte immaginaria. La funzione esponenziale complessa ha 2πZ come periodo. Perciò si definisce la funzione logaritmo complesso logz tramite

Se si restringe il valore dell'argomento in 0≤argz⟨2π, allora si ottiene un unico logz che viene scritto come Logz. In generale, w è determinato solo a meno di una costante additiva contenuta in 2πZ. Questo significa che la versione complessa della formula usuale

non è così semplice come nel caso reale, e cioè, l'integrale

dipende non solo da z ma anche dal cammino di integrazione seguito per andare da 1 a z nel piano di Gauss C. Il punto di vista geometrico è nuovamente di aiuto per superare questa difficoltà. Per un cammino γ che congiunge 1 e z, si conta quante volte γ gira intorno all'origine in verso antiorario e si indica con Ind(γ;0) il numero di tali avvolgimenti. Allora si ha che

In questo modo si comprende concettualmente la natura a più valori di tale funzione logaritmo complesso. Si è così rilevato che senza quelle nozioni basate sull'intuizione geometrica, come lo spazio delle fasi e il numero di avvolgimenti, sarebbe sicuramente difficile comprendere il moto del pendolo ideale o la natura a più valori della funzione logaritmo complesso.

Curvatura: dai problemi classici a quelli di geometria globale

Geometria euclidea e geometria moderna. - Se si confrontano la g. euclidea e la g. cartesiana basata sull'uso del metodo analitico, si osserva che la prima si basa su un piccolo numero di assiomi ed è una g. dello spazio piatto, mentre la seconda è caratterizzata dall'uso delle coordinate di R² e dei calcoli basati su tali coordinate. Nella g. a livello scolastico si studia sia la g. euclidea sia quella cartesiana e in ultimo si arriva a comprendere il problema dell'equivalenza delle due geometrie. Si consideri per es. l'asserzione seguente: "per ogni coppia di punti, esiste una retta che passa per tale coppia e se i due punti sono distinti tale retta è unica". Questa famosa asserzione, che descrive una relazione tra rette e punti, appartiene all'insieme degli assiomi della g. euclidea. Essa viene tradotta nella g. cartesiana come segue: dati due punti p₁=(a₁,b₁) e p₂=(a₂,b₂), la retta che passa per questi due punti è definita dall'equazione

Infatti, se p₁=p₂ allora b₂−b₁ e a₂−a₁ sono uguali a zero e non si ha l'unicità per la retta. Se invece p₁∙p₂, si consideri il seguente sistema di equazioni con incognite α e β:

[3] formula.

Questo sistema di equazioni significa che una retta incognita data dall'equazione αx+βy=γ passa attraverso i due punti p₁ e p₂. Se p₁∙p₂ le soluzioni del sistema sono della forma

[4] formula

dove (α₀,β₀,γ₀) non è identicamente nullo e t è un numero arbitrario diverso da zero. In particolare (α:β:γ) è determinato unicamente dall'equazione [3]. Sebbene la soluzione del sistema di equazioni [3] non sia unica come si vede da [4], tutte queste soluzioni definiscono la stessa retta in R². Questa è la controparte cartesiana dell'assioma euclideo di cui sopra.

Un esempio ulteriore è il cosiddetto assioma di Archimede (v. geometria: Altre ricerche di assiomatica: geometria non archimedea, XVI), che può essere descritto nella terminologia dei limiti dalla seguente condizione:

[5] formula.

L'intuizione geometrica soggiacente a questo assioma può essere descritta come l'idea che si possa estendere indefinitamente ogni segmento rettilineo in entrambe le direzioni; tale condizione ha un significato inaspettatamente profondo in matematica. Infatti, i valori assoluti su Q, cioè le funzioni a valori reali |∙| su Q che soddisfano le seguenti proprietà:

sono date dal valore assoluto usuale e da una famiglia di funzioni che sono classificate essenzialmente dai numeri primi nel modo seguente: per p primo, si definisce |x|_p=p⁻^m se x ∈ Q può esprimersi come x=p^m b/a, dove a e b sono interi che non contengono p come fattore primo. Il valore assoluto usuale viene detto archimedeo (a causa della relazione [5]), mentre |∙|_p viene detto non archimedeo perché la condizione [5] non vale, dato che |p^m|_p=p⁻^m. Nella [5] si deve separare il significato di n^→∞ sotto il limite e il comportamento di |n|in Q munito di un valore assoluto (il quale potrebbe essere uno qualsiasi dei valori assoluti introdotti). Inoltre si è congetturato che le norme del tipo |∙|_p, dette anche norme p-adiche, possano avere delle applicazioni in fisica. Nella matematica moderna, la g. non archimedea (g. basata su |∙|_p) viene studiata con la medesima enfasi data alla g. tradizionale. La branca della matematica moderna che studia queste g. in modo unificato è chiamata g. algebrica aritmetica ed è oggi considerata come una parte importante della matematica. Comunque, l'influenza dell'assioma di Archimede nella g. euclidea è stata inaspettatamente rilevante. Inoltre, esso svolge un ruolo essenziale negli assiomi di completezza e continuità di R (l'insieme dei numeri reali con il valore assoluto usuale). La completezza di R mette su solide fondamenta tutta la teoria analitica delle funzioni, dal calcolo elementare all'analisi 'hard' altamente sofisticata.

Si esamina ora cosa significhi lo 'spazio piatto' della g. euclidea. Questo non è altro che l'esistenza della nozione di spostamento parallelo in R²: un qualsiasi oggetto nel piano può essere trasportato parallelemente in qualsiasi posto si voglia. In questo processo, il cammino lungo il quale il trasporto parallelo viene effettuato non ha alcuna rilevanza. Tale osservazione avrebbe potuto fornire una strada per la scoperta delle geometrie non euclidee, ma la storia della matematica non si è sviluppata seguendo questa direzione. L'assioma più misterioso della g. euclidea afferma che per ogni retta L e per ogni punto P esterno a L esiste una e una sola retta parallela a L e passante per P. Fu solamente agli inizi del 19° sec. che C.F. Gauss, N.I. Lobačevskij e J. Bólyai dimostrarono che questo assioma era indipendente dagli altri, scoprendo così le g. non euclidee (v. geometria: Geometria non euclidea, XVI), in particolare la trigonometria di un piano non euclideo, il quale nella terminologia moderna viene descritto come un piano iperbolico con curvatura costante −1. La g. non euclidea fu trattata inizialmente come una g. basata sugli assiomi della g. euclidea classica (ma con un cambiamento dell'assioma del parallelismo). Gauss aprì la strada a un nuovo tipo di studio della g. occupandosi delle superfici in R³ indipendentemente dai postulati classici e lasciando così da parte ogni presupposto filosofico.

Lo studio della teoria delle superfici di Gauss è un buon punto di partenza per avvicinarsi alla g. moderna: se ne considerano qui di seguito alcuni aspetti essenziali (v. geometria: Continuazione dell'indirizzo differenziale. Gauss, XVI; e curvatura, XII). Localmente una superficie si può scrivere nella forma z=u(x,y). Con un'opportuna traslazione e rotazione di coordinate, si ottiene che

[6] formula.

In questo caso la curvatura gaussiana è il prodotto λμ. Si potrebbe pensare che il processo di mettere la superficie nella forma [6] non sia geometrico, perché basato semplicemente su calcoli analitici. Eppure, se si nota che il gruppo delle isometrie di R³ è generato da traslazioni e rotazioni, il processo per ottenere [6] è, in realtà, geometrico e non dipende dalla scelta delle coordinate. Gauss scoprì che la curvatura gaussiana dipende solamente dalla g. intrinseca della superficie e non dall'immersione della superficie. Il significato di questa proposizione si può spiegare come segue: se M è la superficie, allora la prima forma fondamentale g è uno strumento che permette di misurare gli angoli tra due rette tangenti in un punto di M e le lunghezze delle curve su M. A tale scopo g definisce un prodotto interno in ogni punto di M, il quale fornisce il prodotto interno nello spazio ambiente R³, in modo che l'angolo tra due vettori tangenti u e v sia dato da

e la lunghezza di una curva c:[a,b]^→M sia data da

La prima forma fondamentale viene considerata come una quantità intrinseca della superficie. In effetti, esistono molti modi di immergere una superficie in R³ in modo da ottenere la medesima prima forma fondamentale g: la scoperta di Gauss fu che la curvatura gaussiana dipende solo dalla prima forma fondamentale g e non dall'immersione specifica (la forma in R³) della superficie in considerazione. Per definizione due superfici sono dette isometriche se esiste una mappa che identifica le prime forme fondamentali e quindi la curvatura gaussiana è invariante per isometria; in particolare è impossibile sviluppare una qualsiasi parte di una sfera (come, per es., la superficie della Terra) isometricamente su un piano.

Gauss iniziò anche lo studio della cosiddetta geometria globale, tramite il famoso teorema di Gauss-Bonnet, il quale è considerato come il punto di partenza della teoria dell'indice (v. oltre: Geometria globale, curvatura e teoremi dell'indice).

Geometria riemanniana. - La g. che nasce con l'opera di B. Riemann è una generalizzazione diretta della g. intrinseca delle superfici (v. geometria: Indirizzo metrico nel caso di n dimensioni. Spazi di Riemann, XVI) ed è molto importante notare che la g. riemanniana non è una g. particolare come quella euclidea o quella di Lobačevskij, ma è una g. sviluppata per ogni spazio munito di una nozione di lunghezza e di angolo (esistenza di una forma quadratica positiva in ogni punto). Il punto di vista di Riemann è che l'ipotesi fondamentale della g. sia quella riguardante l'esistenza di un campo g_ij tramite il quale si misurano la lunghezza dei vettori e gli angoli tra due vettori: uno spazio munito di un campo g_ij viene detto una varietà riemanniana. Si considera uno spazio U dotato di coordinate (x¹,…, xⁿ) e munito di una forma quadratica g_ij in ogni punto; i coefficienti di tale forma sono funzioni differenziabili dei punti. Questa è una generalizzazione n-dimensionale di un settore di superficie. In questo contesto la definizione dei vettori tangenti non è ovvia, perché non si suppone che esista uno spazio ambiente euclideo. Per definire la nozione di vettore correttamente, si considerano tutte le possibili coordinate (cioè la g. cartesiana) e si fissa una regola di identificazione delle differenti espressioni cartesiane dello stesso vettore. L'idea fondamentale dietro questa procedura è che le misure dipendano dai calibri (gauge), cioè dalla scelta delle coordinate cartesiane, e che la dipendenza sia data da una funzione lineare dipendente dal punto

[7] formula

dove Tⁱ_(x) e T^j_(y) sono espressioni nelle coordinate (x) e (y) dello 'stesso vettore' T. La funzione lineare dipendente dal punto che trasforma T^j_(y) in Tⁱ_(x) viene quindi espressa in queste coordinate tramite la cosiddetta matrice jacobiana

Nello spazio euclideo, come si è visto, si può trasportare parallelamente un vettore in un qualsiasi posto senza preoccuparsi circa il cammino che viene effettuato, mentre nel caso di uno spazio di coordinate generale U con coordinate (x¹,…, xⁿ), non si può assumere l'esistenza di tale trasporto parallelo a priori, perché il trasporto parallelo ovvio (se si considera U come una parte dello spazio euclideo) non è compatibile con la metrica g_ij (se richiediamo che uno spostamento parallelo sia isometrico rispetto alla metrica g_ij). Per superare questa difficoltà si lavora a livello infinitesimale e si suppone che esista una nozione di spostamento parallelo. Si prendano due punti p e p′ che siano infinitesimalmente vicini in modo che si abbia l'uguaglianza p′−p=dx in un qualche sistema di coordinate (x). Lo spostamento parallelo dei campi vettoriali determinati dalle coordinate viene espresso come

[8] formula.

Definire lo spostamento parallelo equivale perciò a definire le funzioni Γ^k_ij(p), le quali sono note come simboli di Christoffel. Se, per es., si richiede che Π_p,_p′ sia isometrico rispetto alla metrica g_ij e che Γ^k_ij=Γ^k_ji, allora Γ^k_ij è definito in modo univoco come

Benché le condizioni che determinano Γ^k_ij in modo sostanzialmente unico possano variare da problema a problema, la scelta appena fatta ha particolare rilevanza nella g. riemanniana. Segue da [8] che

La quantità

[9] formula

misura la deviazione del campo vettoriale Tⁱ dall'essere parallelo. Questa quantità generalizza il differenziale

Il punto di partenza del calcolo negli spazi curvi è il fatto che le quantità

hanno significato indipendentemente dal sistema di coordinate scelto. Questo significa che l'espressione della formula [9], che può riscriversi come ∇Tⁱ=Σ_jdx^j∇_jT_i, definisce un vettore per ogni (dx) nel senso della validità della regola di trasformazione [7]. Si nota che dTⁱ non è più un vettore. Se si è definita la nozione di spostamento parallelo infinitesimale, si è in grado di trasportare parallelamente un vettore lungo una curva data. Il problema successivo è che il trasporto parallelo da un punto a un altro dipende dalla scelta delle curve che connettono questi punti. La nozione di curvatura appare come la deviazione dall'identità del trasporto parallelo lungo un laccio (cioè lungo una curva chiusa). Sebbene questa definizione di curvatura possa sembrare estremamente ambigua, essa ha una solida base matematica (teorema di Ambrose-Singer) e la curvatura risulta essere un campo tensoriale che è costruito canonicamente a partire dalle derivate della metrica fino al secondo ordine. Per le superfici nello spazio euclideo tridimensionale la curvatura coincide con la curvatura gaussiana.

È opinione assai comune che uno degli scopi ultimi della g. riemanniana moderna sia quello di comprendere l'interazione tra la curvatura e le proprietà globali dello spazio che si sta considerando (proprietà topologiche, l'esistenza di campi tensoriali con proprietà specifiche e così via). Quest'asserzione può sembrare troppo limitativa solo se si restringe il significato di 'curvatura' alla curvatura della g. riemanniana. Infatti, si trovano molti concetti e fenomeni che sono considerati come una 'trasfigurazione' della curvatura nella g. riemanniana. Un esempio piuttosto familiare è la nozione di convessità e concavità. Anche in g. algebrica e nella teoria dei numeri appaiono molti casi di trasfigurazione della curvatura: uno degli esempi più importanti è dato dalla nozione di 'classe canonica'. Nella g. algebrica sui numeri complessi, la classe canonica è definita tramite la curvatura di una metrica hermitiana a sua volta definita sulla varietà algebrica presa in considerazione. I geometri riemanniani contemporanei studiano frequentemente problemi della forma 'Globale^→Locale' o 'Locale^→Globale'. Esempi tipici sono: 1) risultati che deducono una restrizione topologica dello spazio da ipotesi locali di curvatura; 2) risultati che deducono condizioni di curvatura locali da una condizione globale sul comportamento totale delle geodetiche.

Geometria globale, curvatura e teoremi dell'indice. - Il successo nello studio dell'interazione tra g. globale e curvatura è uno dei più importanti risultati della g. del 20° secolo. Il punto di partenza di questo studio è il teorema di Gauss-Bonnet, il quale stabilisce che

dove M è una superficie chiusa con una metrica, K è la curvatura e χ(M) è la cosiddetta caratteristica di Eulero di M (v. anche geometria, App. III). Il lato sinistro è calcolato tramite la curvatura della metrica mentre il lato destro è topologico e perciò indipendente dalle metriche della superficie che si sta considerando. Si consideri ora la teoria di Hodge. Parlando per grandi linee, la teoria di Hodge ci dà un modo per studiare la topologia di una data varietà riemanniana chiusa con strumenti analitici. Per investigare la topologia di una varietà, H. Poincaré introdusse il concetto di 'omologia': una classe di omologia di una varietà M può essere rappresentata, in un certo senso, da una sottovarietà chiusa in M e da due sottovarietà chiuse Y₁ e Y₂ le quali rappresentano la stessa classe di omologia se e solo se esiste una sottovarietà Z con bordo Y₁−Y₂. La totalità delle classi di omologia forma uno spazio vettoriale finito-dimensionale. Lo spazio vettoriale duale è lo spazio delle forme differenziali su M, il quale è dato, per definizione, dagli oggetti integrati sulle classi di omologia. In questo caso tutte le forme differenziali la cui integrazione su un'arbitraria classe di omologia è nulla devono essere considerate nulle. Si ottiene perciò lo spazio duale il quale viene definito come gruppo di coomologia di M. Un elemento di un gruppo di coomologia è un funzionale lineare sullo spazio delle classi di omologia ed è rappresentato da forme differenziali.

Proprio come nel caso del principio di Dirichlet nella teoria del potenziale, W. Hodge si chiese se ci fosse un'unica forma differenziale con norma di Dirichlet minima. Per il teorema di Hodge questo è effettivamente quello che si verifica e perciò si è aperta una strada analitica nello studio delle proprietà globali dello spazio: si tratta di una nuova matematica che è stata inventata nel 20° secolo. Una forma differenziale che ottiene il minimo della norma di Dirichlet è la soluzione di una certa equazione differenziale. La teoria di Hodge può essere generalizzata per un qualsiasi complesso ellittico su una varietà riemanniana chiusa M. In tal modo la teoria descritta in precedenza risulta essere un caso speciale di questa teoria generale; il complesso ellittico in questo caso è dato dalla coppia formata dallo spazio di tutte le forme differenziali e dall'operatore di Eulero-Lagrange che caratterizza le forme differenziali con la norma di Dirichlet minima. Per un dato complesso ellittico si definisce anche l'indice: nel caso della teoria di Hodge questo non è altro che la classica caratteristica di Eulero. L'indice è un concetto completamente globale: infatti si ottiene calcolando la dimensione dello spazio delle soluzioni dell'operatore ellittico che si sta considerando. D'altro lato, se si introduce un fibrato munito di una metrica associato al dato complesso ellittico (questo generalizza la nozione di metrica in g. riemanniana e perciò si ha la nozione di 'curvatura' anche in questa situazione), allora si ottiene in modo canonico un polinomio a coefficienti razionali in termini delle componenti delle curvature di M e E. È ora possibile formulare il teorema di Atiyah-Singer, il quale afferma che

[10] formula.

Si osserva direttamente che questo teorema generalizza il teorema di Gauss-Bonnet: in tal modo si comprende l'enorme influenza del teorema dell'indice di Atiyah-Singer nella g. moderna. Esso appare in molti altri settori della ricerca, non solo nella parte topologica della g. ma anche in g. algebrica (il teorema di Riemann-Roch è un caso speciale del teorema di Atiyah-Singer), in fisica matematica, in analisi complessa e così via. È notevole che la 'curvatura', che è definita in modo puramente locale, svolga un tale ruolo globale attraverso la speciale combinazione delle sue componenti, come si osserva nell'integrando della formula di Atiyah-Singer [10].

Alcuni problemi aperti. - Tutti i concetti della g. differenziale, com'è suggerito dal suo nome, sono definiti usando la differenziazione in vari modi. Nel ricercare quali siano le relazioni tra differenti nozioni geometriche, si incontrano quindi in modo naturale delle equazioni differenziali. Accade con estrema frequenza che equazioni simili appaiano in problemi che sono apparentemente differenti. In molti casi equazioni con un'origine geometrica cadono nell'area più difficile da un punto di vista analitico. Questo significa che l'approccio geometrico produce, in genere, equazioni differenziali con un significato importante. Consideriamo l'esempio della teoria di Einstein della relatività generale: un problema in g. differenziale che ha la sua origine in tale teoria è quello dell'esistenza o non esistenza di una metrica di Einstein su diversi tipi di varietà. I problemi generali di esistenza di questo tipo, così come le loro applicazioni ad altri problemi in matematica, sono delle vere e proprie sfide per i ricercatori. Come nel caso della relatività generale, i problemi che hanno motivazioni nella fisica spesso producono le domande più difficili in matematica e specialmente in g.: per es., molti problemi relativi al tentativo di dare una base matematica alle teorie delle superstringhe sono di questo tipo (v. stringa, App. V). Le metriche di Einstein (più precisamente le equazioni differenziali implicate nel problema di esistenza delle metriche di Einstein) svolgono di nuovo un ruolo essenziale in questi problemi. Una nuova difficoltà che sorge nei problemi qui discussi è la non linearità. Tutte le equazioni implicate nel teorema dell'indice di Atiyah-Singer sono invece lineari.

Altre questioni importanti riguardano la trasfigurazione della curvatura. Si possono citare due esempi classici relativi all'analogia tra teoria delle funzioni complesse e teoria dei numeri. Sebbene questi settori della matematica non possano dirsi parti della g. in senso stretto, è notevole il fatto che la curvatura appaia in entrambi (dopo la trasfigurazione). Il primo esempio è il teorema di Picard, secondo il quale ogni funzione meromorfa non costante su C ha al più due valori eccezionali (i valori che non sono assunti dalla funzione meromorfa in considerazione). Il secondo è il teorema di Roth, il quale afferma, sostanzialmente, che ogni numero irrazionale algebrico reale non è approssimato dai numeri razionali della forma p/q più velocemente dell'ordine di q⁻². Se questi teoremi vengono formulati dopo aver preparato gli strumenti per misurare con quale velocità le funzioni meromorfe o i numeri razionali approssimano un punto, allora la somiglianza diventerà quasi perfetta (in questo caso il teorema di Picard deve essere sostituito dal secondo teorema principale di Nevanlinna). E inoltre negli enunciati approssimativi presenti sopra si osserva il magico numero 2, che appare come il numero dei valori eccezionali nel teorema di Picard e come la velocità di approssimazione nel teorema di Roth. Comprendere la ragione reale del perché 2 appaia in parti della matematica completamente differenti è una sfida per i matematici della fine del 20° secolo. In entrambi i casi 2 ha un'origine nella curvatura. Nel caso di Picard, 2 è la caratteristica di Eulero o, equivalentemente, 2 è il massimo numero n tale che la sfera, privata di n punti, non ammetta una metrica riemanniana completa con curvatura costante negativa. Nel caso di Roth la sua dimostrazione non dice niente intorno al significato geometrico di 2, ma altri risultati nelle approssimazioni diofantee, come il teorema del sottospazio di Schmidt, suggeriscono che l'origine del 2 nel teorema di Roth abbia a che fare con la classe canonica (in g. algebrica) della retta proiettiva. Il problema è quello di trovare un percorso che metta in relazione l'apparire del 2 in entrambi i teoremi.

bibliografia

S. Kobayashi, K. Nomizu, Foundations of differential geometry, New York 1963-69.

V.I. Arnold, Mathematical methods in classical mechanics, New York 1980.

B.A. Dubrovin, A.T. Fomenko, S.P. Novikov, Modern geometry - Methods and applications, New York 1984-85.

S.T. Yau, Nonlinear analysis in geometry, Genève 1986.

J. Roe, Elliptic operators, topology and asymptotic methods, New York 1988.

S. Lang, Number Theory III, Berlin 1990.

T. Sakai, Riemannian geometry, Providence (R.I.) 1992.

J. Jost, Riemannian geometry and geometric analysis, Berlin 1998.

Moto per curvatura media

di Luigi Ambrosio, Giovanni Bellettini

Il moto di una superficie secondo la sua curvatura media (che abbrevieremo con m.c.m.) è stato studiato dai matematici negli ultimi tre decenni del 20° sec. sia per la bellezza intrinseca del problema sia per le sue potenziali applicazioni. Il m.c.m. si inserisce nel contesto dei cosiddetti problemi geometrici di evoluzione, che consistono nello studio di sistemi di equazioni di tipo parabolico definite su varietà (v. varietà, App. IV ed equazioni, in questa Appendice). Esempi importanti di problemi geometrici di evoluzione, oltre al m.c.m., sono le evoluzioni delle mappe armoniche e l'evoluzione di una metrica secondo la curvatura di Ricci, di cui ci limitiamo qui a fornire solo alcuni riferimenti bibliografici (Hamilton 1975, 1982a; Struwe 1996). Il m.c.m. rappresenta un problema modello, la cui comprensione è essenziale per lo studio di problemi più complessi, come il problema di Stefan accoppiato a un'equazione di stato (Visintin 1996) e le evoluzioni anisotrope e cristalline (Cahn, Handwerker, Taylor 1992). Inoltre, il m.c.m. e le sue varianti hanno interessi applicativi, in particolare nella fisica delle transizioni di fase e nel problema del riconoscimento di immagini in computer vision (Alvarez, Lions, Morel 1992; Alvarez, Lions, Crandall et al. 1993); sono stati anche recentemente messi in luce dei legami tra il m.c.m. e la dinamica dei sistemi di spin su un reticolo (De Masi, Orlandi, Presutti et al. 1993; Katsoulakis, Souganidis 1994).

Consideriamo un insieme solido E dello spazio euclideo n-dimensionale Rⁿ, la cui frontiera ∙E sia un'ipersuperficie limitata e regolare; si dice che E (o anche che la frontiera di E) si evolve secondo la curvatura media se ogni punto x di ∙E si muove con una velocità normale uguale alla curvatura media H_∙E(x) di ∙E nel punto x. Per convenzione si orientano gli insiemi con la normale esterna; di conseguenza, la curvatura media risulta negativa per gli insiemi convessi, i quali perciò tendono a contrarsi nel corso dell'evoluzione. Un esempio semplice, ma assai utile, è fornito dall'evoluzione di una sfera di raggio R₀, costituita da superfici sferiche concentriche il cui raggio R(t) soddisfa l'equazione differenziale ordinaria Ṙ=−(n−1)/R, la quale ha come soluzione R(t)= [R²₀−2(n−1)t]¹/². Notiamo che al tempo t=R²₀/(2(n−1)) la sfera si riduce a un punto.

Una proprietà fondamentale del m.c.m. è il cosiddetto principio del confronto: se E₁, E₂ sono due insiemi e se E₁ è contenuto in E₂, allora l'inclusione permane nel corso dell'evoluzione. Tale proprietà può essere usata per determinare vari aspetti qualitativi del m.c.m., confrontando l'insieme iniziale con altri (sfere, per es.) per i quali il m.c.m. è esplicitamente calcolabile. L'interesse geometrico del m.c.m. è anche dovuto al suo stretto collegamento con le superfici di area minima, dato che quest'evoluzione si può interpretare come l'equazione di evoluzione associata all'area della superficie di ∙E. Dunque, una frontiera che si evolve secondo la curvatura media tende, istante per istante, a rendere il più piccola possibile l'area della sua superficie.

Il m.c.m. può essere rigorosamente definito usando un approccio parametrico nel modo seguente: detta Γ la frontiera iniziale, si cercano parametrizzazioni regolari nel tempo e nello spazio f(∙,t):Γ^→Γ_t tali Γche valga il sistema di equazioni paraboliche

ove H_t(x)=H_Γt(x)ν_Γt(x) è il vettore curvatura media di Γ_t in x. Al di là dell'approccio parametrico, di tipo lagrangiano, è anche utile adottare un punto di vista più intrinseco, di tipo euleriano. A tale scopo, è stato osservato che il m.c.m. può essere caratterizzato mediante un'equazione differenziale nella distanza orientata d, nel modo seguente: se E(t) indica un'evoluzione regolare di insiemi solidi in Rⁿ, posto d(x,t)=dist(x,E(t))−dist(x,RⁿE(t)), allora gli insiemi E(t) si evolvono per curvatura media se e solo se risulta ∙d/∙t(x,t)=Δd(x,t) su ∙E(t).

Riguardo al problema dell'esistenza di soluzioni del m.c.m., è nota l'esistenza di un'unica soluzione per tempi piccoli a partire da una frontiera iniziale regolare. Di questo risultato si conoscono varie dimostrazioni: R.S. Hamilton ha sviluppato una teoria generale che è stata applicata al m.c.m. (Hamilton 1982b; Gage, Hamilton 1986 e Huisken 1984; altre dimostrazioni sono apparse in Evans, Spruck 1992 e, per le sole curve, in Angenent 1990). Nel caso in cui l'insieme iniziale E sia contenuto nel piano R² e la sua frontiera si riduca a una curva chiusa limitata, liscia e senza autointersezioni, i risultati ottenuti sono esaurienti: infatti M.A. Grayson ha dimostrato (Grayson 1987; cfr. anche Gage 1984 e Gage, Hamilton 1986) che la curva mantiene le stesse proprietà fino a che non sparisce (come nel caso dell'evoluzione di sfere). Inoltre, nell'istante prima della sparizione la curva tende asintoticamente a diventare sferica. Vanno segnalati anche i lavori di S. Angenent (1990, 1991), in cui vengono considerate evoluzioni di curve non necessariamente semplici, anche su superfici di R³.

In dimensione n≥3 la situazione è molto più complicata: G. Huisken (1984) ha mostrato che gli insiemi regolari, limitati e convessi sono stabili per il m.c.m. Anche in questo caso si ha la contrazione a un punto, con convergenza asintotica a una forma sferica. Il caso in cui la frontiera iniziale Γ₀ sia un grafico della forma

ha delle importanti particolarità: K. Ecker e Huisken hanno infatti dimostrato (1989) che, in ipotesi molto generali su f₀, la soluzione del m.c.m. esiste ed è costituita da grafici Γ_t di funzioni regolari f_t soddisfacenti l'equazione in forma di divergenza

Per n≥3, superfici inizialmente regolari possono sviluppare delle singolarità anche prima di ridursi a un punto. Per singolarità intendiamo, per es., la creazione di 'cuspidi' nelle quali la curvatura media non può essere definita in senso classico. Si possono costruire interessanti esempi nei quali l'insieme si divide, a un certo istante, in due componenti connesse; oppure esempi in cui due parti dell'insieme, inizialmente disgiunte, vengono a contatto. Tutti questi esempi mostrano la necessità di introdurre definizioni deboli di movimenti di insiemi, che consentano di dare comunque un senso all'evoluzione anche dopo la comparsa di eventuali singolarità. Varie sono state le proposte in questa direzione negli ultimi anni, inserite nell'ambito di teorie anche molto distanti, come la teoria geometrica della misura e la teoria delle soluzioni delle equazioni paraboliche nel senso della viscosità. Tra le soluzioni generalizzate considerate nella letteratura matematica segnaliamo quelle di K.A. Brakke (1978), il quale studia i movimenti secondo la curvatura media nel contesto della teoria dei varifolds. Un secondo approccio generalizzato al m.c.m., valido per tutta la classe dei problemi geometrici di evoluzione soddisfacenti la proprietà del confronto, è quello di L.C. Evans e J. Spruck (1991) e di Y.G. Chen, Y. Giga e S. Goto (1991), che considerano le linee di livello delle soluzioni di alcune equazioni differenziali di tipo parabolico completamente non lineari, del tipo della [1], v. oltre. La non linearità delle equazioni non consente di limitarsi a soluzioni classiche: per avere soddisfacenti teoremi di esistenza, unicità e stabilità è necessario considerare soluzioni nel senso debole della 'viscosità', nozione introdotta da M.G. Crandall e P.-L. Lions (v. equazioni: Soluzioni di viscosità, in questa Appendice). Il metodo di Evans, Spruck e Chen, Giga, Goto si può brevemente riassumere come segue. Supponiamo che l'insieme iniziale E sia un aperto con frontiera limitata; si sceglie una funzione uniformemente continua g in modo che ∙E={g=0} e E={g⟨0}; poi si considera l'unica soluzione continua nel senso della viscosità dell'equazione parabolica

[1] formula

che, formalmente, si ottiene imponendo a tutti gli insiemi di livello

di u(∙,t) di evolversi secondo la curvatura media. Gli insiemi Γ_t={x∈Rⁿ:u(x,t)=0} sono l'evoluzione generalizzata di ∙E al tempo t; tali insiemi non dipendono dalla funzione ausiliaria g e l'evoluzione così definita coincide con quella classica finché quest'ultima è definita. Vale inoltre la proprietà del confronto.

Un terzo approccio generalizzato al m.c.m., considerato indipendentemente da E. De Giorgi, da P. De Mottoni e M. Schatzman, da X. Chen, da L. Bronsard e R.V. Kohn, e in seguito da molti altri autori è quello di passare al limite per ε↓0 nell'equazione di Allen e Cahn

[2] formula

dove γ(s)=tanh( ≈̳2s) e d è la distanza orientata da ∙E (De Giorgi 1990, 1991, 1992; Bronsard, Kohn 1991; Chen 1992; Evans, Soner, Souganidis 1992; De Mottoni, Schatzman 1995). La definizione di movimento generalizzato di E viene data allora come segue: supponiamo che E sia un insieme aperto con frontiera limitata e, per ogni ε>0 fissato, indichiamo con u_ε la soluzione della [2]. Si definisce l'evoluzione generalizzata di E al tempo t>0 come {x ∈ Rⁿ : lim sup_ε↓₀ u_ε (x,t)⟨0}. Dal punto di vista variazionale, lo studio del comportamento asintotico delle soluzioni di [2] si collega direttamente allo studio dei minimi del funzionale dell'area, dato che la [2], a meno di un riscalamento temporale, è l'equazione di evoluzione associata al funzionale

Tali funzionali approssimano, nel senso della Γ-convergenza di De Giorgi, il funzionale dell'area quando ε tende a zero (Modica, Mortola 1977; Dal Maso 1993).

Un ulteriore approccio generalizzato al m.c.m. è quello variazionale proposto da F. Almgren, J.E. Taylor e L. Wang (1993), basato su una discretizzazione temporale, con soluzione ricorsiva di opportuni problemi di minimo. Il metodo è stato successivamente generalizzato da De Giorgi (1993), che ha introdotto il concetto di movimento minimizzante.

Un altro metodo per lo studio del m.c.m. è quello delle minime barriere, introdotto da De Giorgi; tale metodo consente di definire in modo intrinseco un'unica soluzione globale del moto per curvatura media anche per evoluzioni di varietà di codimensione arbitraria (De Giorgi 1996, e anche Ambrosio, Soner 1996). L'approccio nel senso delle barriere al m.c.m. per ipersuperfici si può riassumere nel modo seguente. Indichiamo con P(Rⁿ) la classe di tutti i sottoinsiemi Rⁿ e sia ℱ la famiglia di applicazioni definita come segue: f appartiene a ℱ se esistono due numeri reali non negativi a⟨b tali che f:[a,b]^→P(Rⁿ) e f(t) è un insieme solido con frontiera compatta di classe C^∞ che evolve in modo classico per curvatura media per tutti i tempi t∈[a,b]. Un'applicazione ϕ:[0,+∞[^→P(Rⁿ) è una barriera se, data f:[a,b]⊆[0,+∞[^→P(Rⁿ) appartenente a ℱ con f(a)⊆ϕ(a), allora f(b)⊆φ(b). Sia ora E⊆Rⁿ un insieme arbitrario; la minima barriera ℳ(E):[0,+∞[^→P(Rⁿ) è definita da

per ogni t≥0 (sulla teoria delle barriere: Bellettini, Paolini 1995; Bellettini, Novaga 1997).

Esistono altre interessanti nozioni di evoluzione debole per curvatura media; in particolare, T. Ilmanen (1994) ha introdotto il metodo della regolarizzazione ellittica, H.M. Soner ha considerato, nell'ottica delle soluzioni di viscosità, il cosiddetto metodo della funzione distanza, Evans (1993) ha usato l'equazione del calore e la teoria dei semigruppi non lineari e, infine, De Giorgi (1996), riprendendo l'approccio parametrico, ha suggerito l'idea di penalizzare, per così dire, le derivate di ordine alto della parametrizzazione. Le relazioni che intercorrono tra le varie nozioni generalizzate di m.c.m. sopra descritte non sono ancora state del tutto chiarite.

Riguardo al problema della regolarità del m.c.m., vari risultati sono stati ottenuti usando la formula di monotonia di Huisken (Huisken 1991; Ilmanen 1993). Lo studio e la classificazione delle singolarità che si possono presentare durante l'evoluzione sono oggetto in questi anni di molte ricerche (Angenent 1991; Soner, Souganidis 1993; Altshuler, Angenent, Giga 1995; Hamilton 1995).

bibliografia

R.S. Hamilton, Harmonic maps of manifolds with boundary, Berlin 1975.

L. Modica, S. Mortola, Un esempio di Γ-convergenza, in Bollettino dell'Unione matematica italiana, 1977, 14, pp. 285-99.

K.A. Brakke, The motion of a surface by its mean curvature, Princeton 1978.

R.S. Hamilton, Three-manifolds with positive Ricci curvature, in Journal of differential geometry, 1982a, 17, pp. 255-306.

R.S. Hamilton, The inverse function theorem of Nash and Moser, in Bulletin of the American mathematical society, 1982b, 7, pp. 65-222.

M. Gage, Curve shortening makes convex curves, in Inventiones mathematicae, 1984, 76, pp. 357-64.

G. Huisken, Flow by mean curvature of convex surfaces into spheres, in Journal of differential geometry, 1984, 20, pp. 237-66.

M. Gage, R.S. Hamilton, The heat equation shrinking convex plane curves, in Journal of differential geometry, 1986, 23, pp. 69-96.

M.A. Grayson, The heat equation shrinks embedded plane curves to round points, in Journal of differential geometry, 1987, 26, pp. 285-314.

K. Ecker, G. Huisken, Mean curvature flow of entire graphs, in Annals of mathematics, 1989, 130, pp. 453-71.

S. Angenent, Parabolic equations for curves and surfaces I. Curves with p-integrable curvature, in Annals of mathematics, 1990, 132, pp. 451-83.

E. De Giorgi, Some conjectures on flow by mean curvature, in Methods of real analysis and partial differential equations, ed. M.L. Benevento, T. Bruno, C. Sbordone, Napoli 1990.

S. Angenent, Parabolic equations for curves and surfaces II. Intersections, blow-up and generalized solutions, in Annals of mathematics, 1991, 133, pp. 211-37.

L. Bronsard, R.V. Kohn, Motion by mean curvature as the singular limit of Ginzburg-Landau dynamics, in Journal of differential equations, 1991, 90, pp. 211-37.

Y.G. Chen, Y. Giga, S. Goto, Uniqueness and existence of viscosity solutions of generalized mean curvature flow equation, in Journal of differential geometry, 1991, 33, pp. 749-86.

E. De Giorgi, Congetture sui limiti delle soluzioni di alcune equazioni paraboliche quasi lineari, in Nonlinear Analysis. A tribute in honour of G. Prodi, in Quaderni della Scuola normale superiore di Pisa, 1991, pp. 173-87.

L.C. Evans, J. Spruck, Motion of level sets by mean curvature i, in Journal of differential geometry, 1991, 33, pp. 635-81.

G. Huisken, Asymptotic behavior for singularities of the mean curvature flow, in Journal of differential geometry, 1991, 31, pp. 285-99.

L. Alvarez, P.-L. Lions, J.M. Morel, Imagine selective smoothing and edge detection by nonlinear diffusion i, ii, in SIAM Journal of numerical analysis, 1992, 29, pp. 182-93 e pp. 845-66.

J.W. Cahn, C.A. Handwerker, J. Taylor, Geometric models of crystal growth, in Acta metallurgica, 1992, 40, pp. 1443-74.

X. Chen, Generation and propagation of interfaces by reaction diffusion equation, in Journal of differential equations, 1992, 96, pp. 116-41.

M.G. Crandall, H. Ishii, P.-L. Lions, User's guide to viscosity solutions of second order partial differential equations, in Bulletin of American mathematical society, 1992, 27, pp. 1-67.

E. De Giorgi, New ideas in calculus of variations and geometric measure theory, in Motion by mean curvature and related topics. Proceedings of the Conference held in Trento, July 20-24, Berlin 1992, pp. 63-69.

L.C. Evans, H.M. Soner, P.E. Souganidis, Phase transitions and generalized motion by mean curvature, in Communications in pure and applied mathematics, 1992, 45, pp. 1097-123.

L.C. Evans, J. Spruck, Motion of level sets by mean curvature ii, in Transactions of American mathematical society, 1992, 330, pp. 321-32.

F. Almgren, J.E. Taylor, L. Wang, Curvature-driven flows: a variational approach, in SIAM Journal of control and optimization, 1993, 31, pp. 387-437.

L. Alvarez, P.-L. Lions, M.G. Crandall et al., Axioms and fundamental equations of image processing, in Archive for rational mechanics and analysis, 1993, 123, pp. 199-257.

G. Dal Maso, An introduction to Γ-convergence, Boston (Mass.) 1993.

E. De Giorgi, New problems on minimizing movements, in Boundary value problems for partial differential equations and applications, 29, ed. J.-L. Lions, C. Baiocchi, Paris 1993.

A. De Masi, E. Orlandi, E. Presutti et al., Motion by curvature by scaling non local evolution equations, in Journal of statistical physics, 1993, 73, pp. 543-70.

L.C. Evans, Convergence of an algorithm for mean curvature motion, in Indiana University mathematical journal, 1993, 42, pp. 533-57.

T. Ilmanen, Convergence of the Allen-Cahn equation to Brakke's motion by mean curvature, in Journal of differential geometry, 1993, 38, pp. 417-61.

H.M. Soner, Motion of a set by the curvature of its boundary, in Journal of differential equations, 1993, 191, pp. 313-72.

H.M. Soner, P.E. Souganidis, Singularities and uniqueness of cylindrically symmetric surfaces moving by mean curvature, in Communications in partial differential equations, 1993, 18, pp. 859-94.

M.A. Katsoulakis, P.E. Souganidis, Interacting particle systems and generalized mean curvature evolution, in Archive for rational mechanics and analysis, 1994, 127, pp. 133-57.

T. Ilmanen, Elliptic regularization and partial regularity for motion by mean curvature, Providence (R.I.) 1994.

S. Altshuler, S. Angenent, Y. Giga, Mean curvature flow through singularities for surfaces of rotation, in The journal of geometric analysis, 1995, 5, pp. 293-358.

G. Bellettini, M. Paolini, Some results on minimal barriers in the sense of De Giorgi applied to driven motion by mean curvature, in Rendiconti degli atti dell'Accademia nazionale delle scienze detta dei XL, 1995, 19, pp. 43-67.

P. De Mottoni, M. Schatzman, Geometrical evolution of developped interfaces, in Transactions of the American mathematical society, 1995, 347, pp. 1533-89.

R.S. Hamilton, Harnack estimate for the mean curvature flow, in Journal of differential geometry, 1995, 41, pp. 215-26.

L. Ambrosio, H.M. Soner, A level set approach to the evolution of surfaces of any codimension, in Journal of differential geometry, 1996, 43, pp. 693-737.

E. De Giorgi, Congetture riguardanti alcuni problemi di evoluzione; a paper in honour of J. Nash, in Duke mathematical journal, 1996, 81, pp. 255-68.

M. Struwe, Geometric evolution problems, in IAS/Park City Mathematics Series, 1996, 2.

A. Visintin, Models of phase transitions, Boston 1996.

G. Bellettini, M. Novaga, Minimal barriers for geometric evolutions, in Journal of differential equations, 1997, 139, pp. 76-103.