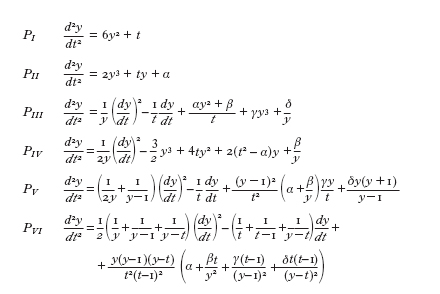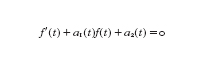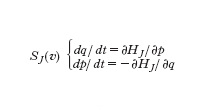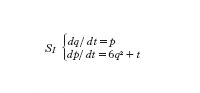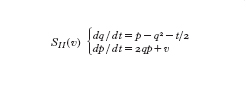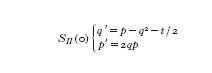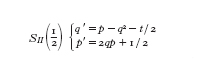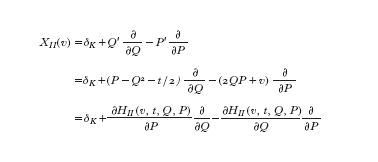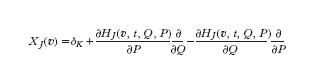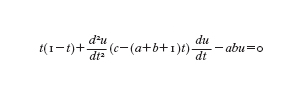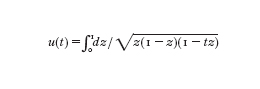EQUAZIONI
Equazioni
(XIV, p. 132; App. III, i, p. 564; IV, i, p. 714; v. equazioni differenziali, App. V, ii, p. 131).
Il concetto generale di e. in matematica è trattato nella voce equazioni del vol. XIV dell'Enciclopedia Italiana, dove tale tema viene discusso nell'ambito dell'analisi matematica; nella voce si considera - oltre ai gruppi continui di trasformazioni e alla teoria delle trasformazioni di contatto - la risoluzione delle e. associate ai principali problemi della fisica matematica: e. differenziali ordinarie; e. alle derivate parziali del primo ordine, in particolare lineari, ed e. di Monge-Ampère del secondo ordine; e. integrali e integrodifferenziali. Queste ultime sono trattate anche nella voce funzionali (XVI, p. 180), nella quale viene introdotto l'approccio dell'analisi funzionale, che permea la moderna teoria delle e. differenziali. Viene inoltre discusso il legame tra il calcolo delle variazioni e la teoria delle e. differenziali (v. variazioni, calcolo delle, XXXIV, p. 1001). Nelle Appendici si distingue il problema del calcolo numerico degli integrali, uno dei settori fondamentali dell'analisi numerica moderna (v. numerici, calcoli, App. III, ii, p. 286; IV, ii, p. 628 e computazionali, metodi, in questa Appendice), dai problemi analitici formulabili in modo generale con il linguaggio dell'analisi funzionale e nella cui risoluzione intervengono anche altri settori della matematica, come la topologia. Per quanto riguarda la teoria delle e. differenziali, si descrive l'approccio qualitativo nello studio delle e. non lineari (equazioni, App. III e IV) fino allo sviluppo della teoria della biforcazione e della teoria dei sistemi dinamici, uno dei settori più caratteristici della moderna matematica pura e applicata (equazioni differenziali, App. V; v. sistemi dinamici, in questa Appendice); nel campo delle e. alle derivate parziali vengono registrati vari contributi allo studio delle e. semilineari del second'ordine, ellittiche e paraboliche (equazioni, App. III e IV), e alle e. del primo ordine, anche con l'introduzione di soluzioni diverse da quelle classiche (equazioni differenziali, App. V).
La teoria delle e. algebriche è presentata invece nella voce algebra (II, p. 421) e nelle voci dedicate specificamente alle e. algebriche lineari e al loro significato geometrico: determinanti (XII, p. 691) e coordinate (XI, p. 294). In queste ultime due voci viene introdotto un settore classico, l'algebra lineare, il quale, grazie anche allo sviluppo delle tecniche di calcolo numerico implementabili con l'elaboratore elettronico, svolge ancora oggi un ruolo fondamentale nelle applicazioni in diverse discipline (per es., in ingegneria o in economia) ed è anch'esso una delle colonne portanti dell'insegnamento della matematica applicata; la risoluzione numerica di sistemi lineari è considerata sotto la voce equazioni (App. III), nella voce numerici, calcoli (XXV, p. 29; App. III e IV) e nella voce computazionali, metodi (in questa Appendice).
In questa voce vengono trattati gli sviluppi recenti relativi ad alcuni temi significativi sia da un punto di vista storico sia per le applicazioni e le prospettive future. In primo luogo si discutono i progressi compiuti relativamente a problemi classici quali il grado di generalità del teorema della divergenza, il xix problema di Hilbert (regolarità dei minimi lipschitziani nel calcolo delle variazioni) e il problema di Plateau per le superfici minime. Quest'ultimo caso è di particolare importanza per lo studio delle superfici libere dei liquidi. Nella seconda parte viene presentata la teoria delle soluzioni di viscosità per le e. alle derivate parziali non lineari. Tale strumento rientra, in un certo senso, nell'ambito delle tecniche che permettono di risolvere e. differenziali tramite l'uso di opportuni spazi funzionali di 'soluzioni generalizzate'. Infine si presentano i risultati moderni relativi alla formalizzazione della nozione di 'funzione classica'. In questo ambito svolgono un ruolo fondamentale una classe di e. scoperte da Painlevé e una serie di tecniche, marcatamente algebriche, che sono in relazione con le versioni differenziali della teoria di Galois per le e. algebriche. *
Equazioni alle derivate parziali e calcolo delle variazioni
di Mario Miranda
Insiemi di perimetro finito e teorema della divergenza. - Il teorema fondamentale del calcolo integrale (v. integrale, calcolo, XIX) ha una naturale estensione alle funzioni F: Rn→Rn, cioè alle n-uple di funzioni reali di n variabili reali. Posto
definita la divergenza di F mediante
e supposte continue le n funzioni reali di n variabili reali D₁f₁,…, Dnfn, allora per ogni intervallo Δ=(a₁,b₁)×…×(an,bn) di Rn l'integrale multiplo ∫Δ divF(x)dx può essere calcolato con integrazioni delle componenti della funzione F sulle facce del bordo ∙Δ dell'intervallo Δ. Si ha la seguente identità
dove ν(x) è il versore normale esterno sulle facce di ∙Δ e ℋn⁻¹ la misura (n−1)-dimensionale sulle stesse. È ovvio che i due membri dell'identità qui sopra scritta abbiano significato per domini con geometria molto più sofisticata di quella degli intervalli n-dimensionali. La validità della formula, detta teorema della divergenza e anche formula di Gauss-Green, era ben nota per domini poliedrici, sferici, conici e per moltissimi altri (sulle teorie della misura e dell'integrazione moderne, v. funzionale, analisi, App. IV). Tuttavia fino a tutta la prima metà del Novecento non si era mai posto il problema di descrivere con un'opportuna definizione la famiglia di tutti i domini n-dimensionali per i quali valga il teorema della divergenza. Nel 1951, a Taormina, durante i lavori del iv Congresso dei matematici italiani, R. Caccioppoli affermava: "Al calcolo integrale manca tuttora una teoria dell'integrazione a k dimensioni in uno spazio a n dimensioni (k〈n): una teoria, paragonabile per generalità a quella di Lebesgue dell'integrazione n-dimensionale, fondata su nozioni semplici ed esaurienti di misura e di integrale k-dimensionali, e culminante in una estensione definitiva dei teoremi integrali sulle forme differenziali (formule di Green-Stokes). Le numerose ricerche in questa direzione non ispirate a un programma organico, sono sempre circoscritte nello scopo; frammentari i risultati, pur notevoli. Basti ricordare la molteplicità quasi caotica delle definizioni di misura lineare o superficiale (Carathéodory, Gross, Hausdorff, Kolmogoroff ecc.), la serie di esempi intesi a dimostrare queste a coppie non equivalenti tra loro, e le varie estensioni parziali della formula di Gauss-Green (Schauder, Federer, Lorentz ecc.), spesso di una generalità artificiosa".
La conferenza di Taormina e una serie di note lincee apparse nell'anno successivo, non dettero quanto Caccioppoli sembrava essere sicuro di poter offrire. Ciò permise a L.C. Young (recensore di tali note) di difendere i matematici accusati di aver fatto troppo poco e di esprimere dubbi sulle congetture di Caccioppoli. Ma nella primavera del 1953, E. De Giorgi annunciava di aver risposto alla domanda più sopra formulata sulla validità del teorema della divergenza e di aver quindi dimostrato quanto Caccioppoli aveva previsto nel caso k=n−1. L'anno successivo De Giorgi pubblicò tutti i dettagli del suo lavoro che così spiegava: "La teoria della misura sviluppata in questo lavoro concerne le frontiere di insiemi di uno spazio euclideo Sr; tali frontiere non sono riguardate come semplici insiemi di punti ma come insiemi orientati, per i quali si definisce non solo la misura assoluta ma anche la misura relativa delle proiezioni su un qualunque iperpiano. I fondamenti di questa teoria sono stati posti recentemente da R. Caccioppoli (in generale per la misura (r−h)-dimensionale); contemporaneamente ed indipendentemente io ero pervenuto agli stessi risultati, partendo da un punto di vista e con intenti diversi. Caccioppoli si è proposto di dare una teoria generale dell'integrazione delle formule di Green-Stokes. Il mio scopo invece era inizialmente una generalizzazione sostanziale di certi problemi isoperimetrici e partivo dalla formula di Gauss-Green come istanza a priori". Nel 1955 De Giorgi pubblicò un secondo articolo contenente una profonda analisi delle proprietà geometriche delle frontiere degli insiemi di perimetro finito grazie alla quale fu in grado di scrivere il teorema generale della divergenza nella forma classica. Questa indagine gli fornì uno strumento con il quale egli diede nel seguito una risposta di eccezionale valore agli annosi problemi riguardanti le varietà di codimensione uno e di misura minima.
Il diciannovesimo problema di Hilbert
Il problema dell'elettrostatica, studiato fra gli altri da K.F. Gauss, P.G.L. Dirichlet, K. Weierstrass, C. Arzelà e infine da D. Hilbert, è il seguente: fissata una regione limitata Ω dello spazio euclideo a tre dimensioni, fissata una funzione reale φ continua sulla frontiera ∙Ω di tale regione, si vuole dimostrare l'esistenza di una funzione reale V, continua su Ω ∙Ω, la quale coincida con φ su ∙Ω e abbia derivate prime e seconde continue su Ω, ivi soddisfacenti l'e. di Laplace. Essendo le soluzioni dell'e. di Laplace (dette anche funzioni potenziali o funzioni armoniche) caratterizzate nell'ambito di tutte le funzioni continue dalla proprietà della media, è facile provare l'unicità della soluzione del problema. È altrettanto facile dimostrare che il problema può non avere soluzione. Gauss aveva indicato un problema R da associare al problema dell'elettrostatica P, ove questo fosse risolubile seguendo il procedimento tipico dell'analisi matematica (v. analisi, III). Si tratta del seguente problema variazionale: cercare fra tutte le funzioni reali f continue su Ω ∙Ω ed eguali alla φ su ∙Ω, quella per la quale l'integrale
assume il valore minimo.
Hilbert indicò condizioni sui dati Ω, φ sufficienti per la soluzione del problema R nell'ambito delle funzioni lipschitziane. La verifica della validità della proprietà della media per tale funzione minimizzante permette di affermare che essa è soluzione del problema P. Questo metodo può essere applicato a un'ampia classe di e. differenziali che include molte e. interessanti per la fisica matematica. Le funzioni lipschitziane soluzioni del problema R, per poter essere soluzioni del problema P, devono essere dotate di derivate prime e seconde continue. Nel caso dell'elettrostatica questo passo era una facile conseguenza della proprietà della media, conseguenza a sua volta della proprietà variazionale. In generale non esiste un ausilio equivalente a quello fornito dalla proprietà della media. Ciononostante Hilbert era convinto che il suo metodo potesse continuare a essere fecondo ben oltre l'e. di Laplace ed espresse tale convinzione in un passo della storica conferenza tenuta a Parigi nel 1900, in occasione del ii Congresso internazionale dei matematici. La conferenza conteneva l'indicazione di ventitré problemi aperti, il diciannovesimo dei quali comprendeva la dimostrazione della regolarità dei minimi lipschitziani. La difficoltà maggiore di tale dimostrazione risultò essere, nel tempo, la prova dell'esistenza delle derivate prime continue. Un procedimento per tale dimostrazione fu illustrato da De Giorgi in un intervento al v Congresso dei matematici italiani, tenuto a Pavia nel 1955. La memoria di De Giorgi, contenente tutti i dettagli della risoluzione del xix problema di Hilbert, fu presentata dal suo maestro M. Picone all'Accademia delle scienze di Torino nell'aprile del 1957. Il 26 maggio 1958 la redazione dell'American journal of mathematics ricevette un articolo di J. Nash contenente notevoli risultati riguardanti le soluzioni delle e. differenziali paraboliche e di quelle ellittiche, viste come limiti asintotici delle prime. Fra questi ultimi risultati si ritrova il teorema di De Giorgi, quindi un'altra soluzione del xix problema. La coincidenza di due risoluzioni indipendenti e pressoché contemporanee di un annoso problema fu ritenuta singolare e addirittura stupefacente, considerata l'originalità e la potenza dei metodi creati da De Giorgi e Nash.
Il lavoro di De Giorgi si ricollega alla risoluzione del problema isoperimetrico che lo stesso aveva data con la definizione degli insiemi di perimetro finito: per ogni insieme misurabile E di Rn vale la disuguaglianza
dove c(n) è un valore numerico dipendente solo dalla dimensione dello spazio e tale che
se e solo se E è la sfera n-dimensionale. Partendo dalla disuguaglianza isoperimetrica e da una disuguaglianza integrale per le soluzioni dell'e. differenziale ellittica, De Giorgi mise a punto un geniale ed elementare procedimento per la dimostrazione della continuità delle derivate prime delle soluzioni.
Da parte sua Nash (1958) sottolineava le importanti conseguenze che avrebbero avuto i suoi risultati: "Il successo nel trattamento di equazioni differenziali non lineari dipende generalmente da previsioni sul comportamento delle soluzioni. Queste previsioni consistono in Teoremi riguardanti le equazioni lineari con coefficienti variabili ed esse implicano proprietà di compattezza per la classe delle possibili soluzioni. In alternativa, le valutazioni a priori possono servire a dimostrare la regolarità delle soluzioni generalizzate. Le stime più potenti danno informazioni quantitative sulla continuità delle soluzioni senza richiedere informazioni quantitative sulla continuità dei coefficienti". Dopo aver osservato come pochissimi dei molti risultati relativi al caso di due variabili fossero stati, fino a quel momento, dimostrati per tre o più variabili, Nash affermava che i suoi risultati saldavano quella frattura e avrebbero reso possibile costruire una teoria generale delle e. non lineari paraboliche ed ellittiche, senza alcuna restrizione dimensionale. Egli ricordava inoltre che i metodi utilizzati erano stati ispirati da un'intuizione di carattere fisico anche se il rituale dell'esposizione matematica tendeva a nascondere questa origine, e che le e. paraboliche trovano utile interpretazione nel fenomeno della diffusione, del moto browniano, dei flussi di calore e di cariche elettriche.
Nash aveva parlato delle proprietà di compattezza che i nuovi metodi, necessari per risolvere il xix problema, avrebbero permesso di dimostrare. De Giorgi, aiutato dal suo allievo S. Spagnolo, studiò le conseguenze della compattezza delle soluzioni di e. diverse sottoposte a uno stesso controllo della ellitticità. Alla conseguente convergenza di tali soluzioni fu dato il nome di G-convergenza. I lavori del nuovo campo di ricerca cominciarono a essere pubblicati sul finire degli anni Sessanta, e la produzione fu molto intensa per oltre un ventennio. L'idea fu di utilizzare una tecnica analoga a quella che era stata adoperata nel teorema di Peetre sulla caratterizzazione funzionale degli operatori differenziali in termini di supporti per chiarire un fenomeno sul quale De Giorgi aveva a lungo meditato: in una famiglia di problemi di Dirichlet per e. equi-ellittiche del secondo ordine con coefficienti dipendenti da un parametro, le soluzioni possono avere un comportamento limite diverso da quello che si otterrebbe eseguendo semplicemente il limite debole dei coefficienti. Il fenomeno si presenta con chiarezza nel caso particolare delle e. ordinarie su un intervallo {α≤t≤β}, cioè
dove i coefficienti ak(t) sono delle funzioni a scalino che assumono alternativamente due distinti valori positivi λ, Λ, su intervallini di ampiezza 2⁻k(β−α). Quando k→∞, la corretta e. limite è quella che ha per coefficienti la media armonica 2λ/(λ+Λ) dei due valori, mentre il limite debole dei coefficienti è la media aritmetica (λ+Λ)/2. Questo semplice esempio, tramandato come 'l'esempio di De Giorgi', si trova alla base di tutta la teoria. Secondo Spagnolo, il lavoro di De Giorgi si proponeva di approfondire alcuni aspetti piuttosto oscuri della dimostrazione di Nash del teorema di regolarità hölderiana, mentre il problema fisico dell'omogeneizzazione non si era ancora profilato all'orizzonte.
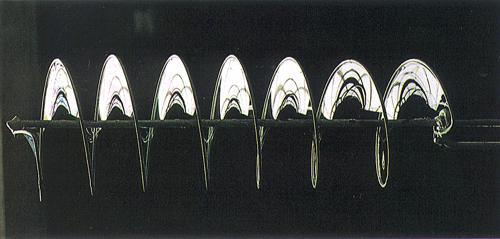
Il problema di Plateau. - Come particolare problema trattabile col suo metodo di calcolo delle variazioni per gli integrali doppi, J.L. Lagrange considerò la superficie d'area minima fra tutte quelle che passano per un determinato contorno chiuso (v. superficie, XXXIII, p. 8). Tale problema fu risolto sperimentalmente da J.A.F. Plateau realizzando materialmente il contorno C con del filo metallico e immergendolo in una soluzione formata da acqua e sapone: il filo, estratto con cautela, riappariva 'riempito' da una lamina liquida soddisfacente (per ragioni fisiche) le condizioni richieste a una superficie d'area minima (v. fig. A e B). Lo stesso Plateau dedicò molta attenzione alle superfici libere dei liquidi nei tubi capillari e studiò il comportamento di alcune gocce d'olio sospese in un fluido: quest'esperimento permetteva di verificare la teoria di Laplace sulla formazione dei corpi nel sistema solare. Le superfici di area minima, le superfici di livello nei capillari e quelle racchiudenti le gocce d'olio sospese in un fluido hanno proprietà differenziali analoghe riguardanti il valore della curvatura media in ogni loro punto. Nel primo caso questo valore è nullo, negli altri casi è esprimibile mediante i dati del problema.
L'analisi matematica di questi fenomeni, mirante alla dimostrazione dell'esistenza della soluzione, non fece passi degni di nota nell'Ottocento. Il primo problema, in ipotesi speciali per la curva C, è simile a quello dell'elettrostatica in due variabili: si tratta di dimostrare l'esistenza di una funzione minimizzante l'integrale
con il vincolo f(x, y)=φ(x, y) per (x, y) ∈ ∙Ω, dove φ è una funzione continua assegnata. Il metodo di Hilbert per l'elettrostatica è applicabile a questo nuovo integrale doppio, ma fu necessario attendere la pubblicazione di un articolo di T. Rado, nel 1930, per vedere una dimostrazione completa dell'esistenza della soluzione per ogni dominio Ω convesso e limitato e per ogni funzione continua φ. Tuttavia, il problema risolto da Rado per contorni C grafici di funzioni continue sul bordo di una regione convessa piana non era sufficiente per la verifica matematica degli interessanti fenomeni evidenziati dagli esperimenti di Plateau, con contorni topologicamente più sofisticati. Negli anni successivi furono spese molte energie per potenziare la teoria matematica delle superfici minime. La massa dei risultati ottenuti da J. Douglas e altri nella dimensione della realtà fisica fu resa possibile dalla fortunata circostanza della disponibilità di strumenti matematici 'adattabili' allo scopo, come le funzioni olomorfe di una variabile complessa e le funzioni armoniche di due variabili reali. Ma l'utilizzo di questi strumenti comportava ancora restrizioni di tipo topologico per il dato C, restrizioni prive di motivazioni oggettive. Per superare questa difficoltà occorreva rinunciare alla peculiarità della dimensione fisica. Bisognava cioè vedere il problema in dimensione n in modo da essere costretti a sviscerarne il significato matematico.
All'inizio degli anni Sessanta E.R. Reifenberg e De Giorgi pubblicarono le loro soluzioni del 'vero' problema di Plateau. Si può dire che il vero problema di Plateau per Reifenberg era diventato la minimizzazione di varietà k-dimensionali nello spazio euclideo a n-dimensioni. De Giorgi si limitava invece a minimizzare il perimetro delle frontiere d'insieme, cioè il caso k=n−1. Le due soluzioni non sono di facile confronto per la grande complessità degli oggetti matematici introdotti da Reifenberg. La relativa facilità del metodo di De Giorgi e la prematura morte di Reifenberg, avvenuta nel 1964, favorirono la diffusione dell'approccio tramite frontiere minime. A proposito della 'facilità' del lavoro di De Giorgi, ricordiamo che questi ottenne il successo grazie a una laboriosa approssimazione delle frontiere minime con ipersuperfici che sono grafici di funzioni armoniche in (n−1) variabili. Successivamente F.J. Almgren fu capace di unire alla semplicità di De Giorgi la generalità di Reifenberg dimostrando la regolarità quasi ovunque dei varifolds di misura minima. U. Massari ha esteso il metodo De Giorgi allo studio delle frontiere con curvatura media assegnata (non necessariamente nulla), e analogo lavoro è stato fatto da W.K. Allard per i varifolds. Questi lavori contribuirono allo sviluppo delle teorie matematiche riguardanti la capillarità e la formazione dei pianeti. Successivi raffinamenti degli strumenti approntati da De Giorgi per la risoluzione dei problemi di Plateau hanno permesso allo stesso De Giorgi e ai suoi allievi di fare notevoli progressi nella trattazione matematica di uno dei problemi della visione artificiale, il problema del riconoscimento, o meglio ricostruzione, delle immagini nella formulazione di D. Mumford e J. Shah. Com'è naturale e richiesto dai problemi della tecnologia, gli approcci di De Giorgi e Almgren ai problemi stazionari hanno avuto un'estensione al caso dinamico. Il primo lavoro in questa direzione è di K.A. Brakke, allievo di Almgren. Il nuovo filone di ricerca, riguardante l'e. parabolica associata all'operatore curvatura media, ha portato a risultati di notevole interesse matematico e applicativo (v. geometria: Moto per curvatura media, in questa Appendice).
La congettura di Hilbert sulla regolarità delle soluzioni delle e. ellittiche, provata da De Giorgi e Nash per una singola e., può essere intesa in maniera più ampia. Gli studiosi di e. differenziali vi lessero il suggerimento a indagare la regolarità delle soluzioni dei sistemi ellittici (Morrey 1966). I cultori della teoria geometrica della misura, ramo moderno del calcolo delle variazioni (Federer 1969), si dedicarono con molto impegno alla risoluzione del problema delle singolarità lasciato aperto dai metodi di De Giorgi e Almgren. Nel 1968 i loro sforzi furono coronati da successo nello spazio a sette dimensioni con l'intervento di un grande esperto di geometria differenziale classica, J. Simons. Intanto, la diffusione della conoscenza dei nuovi metodi portò alla possibilità di attaccare il problema della regolarità per le soluzioni dei problemi ellittici. Morrey, ascoltando l'intervento di Almgren al Congresso internazionale dei matematici tenuto a Mosca nel 1966, intuì che anche il caso dei sistemi poteva essere attaccato partendo da un'ipotesi aggiuntiva di regolarità debole. Nel 1968 fu pubblicato il primo articolo dello stesso Morrey, contenente la dimostrazione di un teorema di regolarità quasi ovunque per le soluzioni di una classe di sistemi ellittici. Contemporaneamente De Giorgi aveva indicato l'esistenza di un sistema lineare ellittico a coefficienti discontinui con soluzioni discontinue. Si era così toccato il limite di validità delle teorie di De Giorgi e Nash. E. Giusti e M. Miranda hanno approfondito l'analisi del controesempio di De Giorgi e dimostrato un teorema di regolarità del tipo di Morrey, mentre, indipendentemente, G. Mazya ha messo in luce l'esistenza di soluzioni discontinue per i sistemi ellittici.
Infine, il salto di Reifenberg, De Giorgi e Almgren nella dimensione n ha dato un grande impulso allo studio dell'e. n-dimensionale delle superfici minime. Miranda, avvalendosi della stima del gradiente delle soluzioni dell'e. delle superfici minime, dimostrata nel 1968 in collaborazione con E. Bombieri e De Giorgi, ha esteso il lavoro di Rado, confermando l'intuizione di H. Jenkins e J. Serrin che l'ipotesi di convessità del dominio bidimensionale sia un caso particolare dell'ipotesi generale di curvatura media non negativa delle frontiere dei domini n-dimensionali. D'altra parte era nota, fin dal 1962, una congettura di W.H. Fleming sulla dimostrabilità in ogni dimensione di un famoso enunciato bidimensionale di S. Bernstein del 1910: oltre alle funzioni a gradiente costante, non esistono soluzioni dell'e. delle superfici minime definite per ogni valore delle variabili. Un'osservazione di Fleming, perfezionata da De Giorgi, derivava la verità dell'enunciato di Bernstein per n variabili dalla non esistenza di frontiere minime singolari (n−1)-dimensionali. Il teorema di Bernstein per funzioni di sette variabili era perciò un corollario del teorema di Simons di cui si è detto. Lo stesso Simons aveva indicato nella frontiera singolare dell'insieme
un possibile controesempio al teorema di regolarità. Questa congettura è stata dimostrata nel 1969 da Bombieri, De Giorgi e Giusti, i quali hanno provato altresì l'esistenza di una funzione f definita su tutto R⁸, soluzione dell'e. delle superfici minime e tale che
Questa funzione f non può avere gradiente costante, cioè non è una soluzione banale.
bibliografia
E. De Giorgi, Su una teoria generale della misura (r-1)-dimensionale in uno spazio a r dimensioni, in Annali di matematica pura e applicata, 1954, pp. 191-213.
E. De Giorgi, Nuovi teoremi relativi alle misure (r-1)-dimensionali in uno spazio a r dimensioni, in Ricerche di matematica, 1955, pp. 95-113.
E. De Giorgi, Sulla differenziabilità e l'analiticità delle estremali degli integrali multipli regolari, in Memorie dell'Accademia delle scienze di Torino (Classe di Scienze matematiche, fisiche e naturali), 1957, pp. 25-43.
J. Nash, Continuity of solutions of parabolic and elliptic equations, in American journal of mathematics, 1958, pp. 931-54.
E.R. Reifenberg, Solution of the Plateau problem for m-dimensional surfaces of varying topological type, in Acta mathematica, 1960, pp. 1-92.
F.J. Almgren, Plateau problem. An invitation to varifold geometry, New York-Amsterdam 1966.
C.B. Morrey, Multiple integrals in the calculus of variations, New York 1966.
E. De Giorgi, Un esempio di estremali discontinue per un problema variazionale di tipo ellittico, in Bollettino dell'Unione matematica italiana, 1968, pp. 135-37.
E. Giusti, M. Miranda, Un esempio di soluzioni discontinue per un problema di minimo relativo ad un integrale regolare del calcolo delle variazioni, in Bollettino dell'Unione matematica italiana, 1968, pp. 1-8.
C.B. Morrey, Partial regularity results for non linear elliptic systems, in Journal of mathematics and mechanics, 1968, pp. 649-70.
J. Simons, Minimal varieties in riemannian manifolds, in Annals of mathematics, 1968, pp. 62-105.
E. Bombieri, E. De Giorgi, E. Giusti, Minimal cones and the Bernstein theorem, in Inventiones mathematicae, 1969, pp. 243-69.
H. Federer, Geometric measure theory, Heidelberg-New York 1969.
E. De Giorgi, F. Colombini, L.C. Piccinini, Frontiere orientate di misura minima e questioni collegate, Pisa 1972.
Mathematical developments arising from Hilbert problems, ed. F.E. Browder, Providence (R.I.) 1976.
U. Massari, M. Miranda, Minimal surfaces of codimension one, Amsterdam 1984.
R. Finn, Equilibrium capillary surfaces, Heidelberg-New York 1986.
E. Giusti, Metodi diretti nel calcolo delle variazioni, Bologna 1994.
Geometry V, ed. R. Ossermasn, in Encyclopaedia of mathematical sciences, vol. 90, Berlin-Heidelberg 1997.
Soluzioni di viscosità
di Piermarco Cannarsa
La nozione di soluzione di viscosità introdotta da M.G. Crandall e P.-L. Lions (1983), perfezionata da Crandall, L.C. Evans e Lions (1984) e, successivamente, sviluppata da molti altri autori, appartiene a un capitolo recente della teoria delle e. differenziali alle derivate parziali totalmente nonlineari del primo o del secondo ordine (v. equazioni differenziali, App. V). Per illustrare il contesto cui si applicano le soluzioni di viscosità, si consideri un'e. del primo ordine, la cui forma generale è
dove Ω è un aperto di RN, u è una funzione definita su Ω, ∇u il gradiente di u e F è una funzione regolare definita su Ω×R×RN. Esempi di e. di questo tipo sono l'e. iconale |∇u|²=1 dell'ottica geometrica, la classica e. di Hamilton-Jacobi della meccanica e del calcolo delle variazioni, e, più in generale, l'e. di Hamilton-Jacobi-Bellman connessa con la teoria del controllo ottimo. Un problema fondamentale per le e. del primo ordine consiste nel cercare una soluzione di [1], continua su Ω (la chiusura di Ω), che assuma come valore il dato
dove Γ è una superficie regolare in Ω (per es. Γ può coincidere con la frontiera di Ω) e g è una funzione assegnata, anch'essa regolare. Per risolvere questo problema in casi sufficientemente generali è essenziale poter disporre di una nozione di soluzione non troppo restrittiva. Infatti, è noto che, se ci si limita alla ricerca di soluzioni classiche (cioè di funzioni u, differenziabili con continuità in Ω, che verificano l'e. in ogni punto x di Ω), allora il problema [1]-[2] non è risolubile su tutto Ω ma solo in un opportuno intorno di Γ. Una semplice spiegazione di questo fenomeno è fornita dal classico 'metodo delle caratteristiche' (Courant, Hilbert 1953).
Per dimostrare l'esistenza di una soluzione globale (ossia su tutto Ω) del problema precedente, si è quindi dovuta estendere la nozione di soluzione. Uno spazio in cui si sono cercate soluzioni generalizzate del problema [1]-[2] è quello delle funzioni u che sono lipschitziane in Ω (cioè tali che |u(x)−u(y)|≤K|x−y| per un'opportuna costante K>0 e per ogni scelta di x, y in Ω), imponendo che l'e. sia soddisfatta quasi ovunque in Ω. La scelta di questa nozione di soluzione generalizzata è suggerita dal fatto che, per il teorema di Rademacher, una funzione lipschitziana è differenziabile quasi ovunque in Ω. Questa metodologia ha portato a risultati di esistenza abbastanza generali (Lions 1982). Tuttavia, si danno facilmente esempi che mostrano come il problema [1]-[2] possa avere più soluzioni - addirittura infinite soluzioni - nella classe delle funzioni lipschitziane. Inoltre, tale classe di soluzioni non è stabile rispetto alla convergenza uniforme, vale a dire che una successione di soluzioni di una data e. può convergere uniformemente a un limite che non è una soluzione generalizzata della medesima equazione. La mancanza di unicità e di stabilità rende questa teoria di scarso interesse dal punto di vista delle applicazioni, perché queste due proprietà sono tipiche di qualsiasi modello fisico. Per questo motivo si è reso necessario sviluppare un'ulteriore nozione di soluzione, per cui si abbia non solo esistenza globale, ma anche unicità e stabilità rispetto alla convergenza uniforme. Le soluzioni di viscosità rispondono a pieno a questa esigenza.
Definizione e principali proprietà
Per chiarire alcuni aspetti della definizione di soluzione di viscosità - e per spiegarne l'etimologia - partiamo dall'analisi di un procedimento asintotico noto come metodo della viscosità evanescente. Per ogni ε>0 sia uε una soluzione dell'e. ellittica
(osserviamo che, in alcuni modelli di fluidodinamica, il termine del secondo ordine −εΔu rappresenta una viscosità: v. viscosità, XXXV; idrodinamica, XVIII; fluidodinamica, App. III, IV e V). Supponiamo che, per ε↓0, le uε convergano uniformemente sui compatti a una funzione u. Si può allora congetturare che il limite u sia soluzione dell'e. del primo ordine [1]. Naturalmente, questa relazione differenziale non può essere interpretata in senso classico - in quanto non si sa nemmeno se u è differenziabile - ma va intesa in senso debole, cioè mediante l'uso di opportune funzioni di verifica. Chiamiamo, a questo proposito, funzione test una qualunque funzione ϕ, dotata di derivate di ogni ordine continue in Ω. Fissata ora una funzione test ϕ, supponiamo che u−ϕ abbia un massimo locale stretto in un punto x₀ di Ω. Con ragionamenti elementari si può allora dedurre che anche uε−ϕ ha un massimo locale in un punto xε di Ω, e che limε↓₀ xε=x₀. Condizione necessaria affinché xε sia un punto di massimo è che ∇(uε−ϕ)(xε)=0 e Δ(uε−ϕ)(xε)≤0. Ne segue che
e quindi, al limite per ε↓0,
Analogamente si verifica che, se u−ϕ ha un minimo locale stretto in x₀, allora
Ciò mostra che l'e. [3] produce, al limite per ε↓0, le disuguaglianze [4] e [5]. La definizione di soluzione di viscosità altro non è che un'assiomatizzazione di queste relazioni. Una funzione u, continua su Ω, è detta sottosoluzione di viscosità di [1] se - per ogni funzione test ϕ - vale la [4] in ogni punto di massimo locale per u−ϕ, mentre è detta soprasoluzione di viscosità di [1] se vale la [5] in ogni punto di minimo locale per u−ϕ. Una soluzione di viscosità di [1] è una funzione che sia, allo stesso tempo, sottosoluzione e soprasoluzione dell'equazione. Le proprietà delle soluzioni di viscosità sono state oggetto di un'intensa attività di studio e di ricerca nel corso degli anni Ottanta e Novanta, che ha permesso di costruire una teoria rispondente a tutte le esigenze fin qui descritte. Una caratteristica notevole di questa teoria è l'estrema semplicità con cui si ottengono risultati di esistenza - ne è un esempio l'elegante tecnica di H. Ishii (1987), che adotta il classico metodo di Perron -, stabilità e unicità per il problema [1] con la condizione [2]. L'unicità, in particolare, diventa un corollario del teorema di confronto, il quale stabilisce che se due funzioni u₁ e u₂, uniformemente continue e limitate su Ω, sono, rispettivamente, una sottosoluzione e una soprasoluzione di viscosità dell'equazione λu(x)+F(x,∇u(x))=0 (λ>0), allora dal fatto che u₁≤u₂ su Γ segue che u₁≤u₂ su tutto Ω.
Applicazioni e sviluppi della teoria
Le soluzioni di viscosità forniscono l'ambiente teorico adatto a trattare problemi connessi con perturbazioni singolari di alcuni tipi di e. differenziali, i quali, altrimenti, sarebbero privi di un inquadramento rigoroso. Questa teoria svolge una funzione analoga in molti altri campi di interesse applicativo, quali il controllo ottimo (v. controlli automatici, App. V) e i giochi differenziali. Nella teoria dei controlli si considerano sistemi (fisici, biologici, chimici, economici ecc.) descritti da un'e. di stato del tipo
dove α è una funzione misurabile, detta controllo, che può essere interpretata come un'influenza esterna sull'evoluzione del sistema (per es. l'azione di un motore sulla traiettoria di un aereo, l'introduzione di un vaccino in una popolazione parzialmente infetta o la variazione del tasso di sconto da parte di una banca centrale). Detta yx,α la soluzione dell'e. di stato che assume il dato iniziale y(0)=x, si vuole determinare il controllo α in modo che un funzionale 'costo' della forma
risulti minimo. Il metodo della programmazione dinamica, introdotto da R. Bellman (1957), associa al problema precedente la funzione valore v(x)=infαJ(x, α), la cui conoscenza permette, mediante un opportuno procedimento costruttivo, di risolvere il problema di partenza. Benché in generale non ci si possa attendere che la funzione valore ammetta derivate parziali, nei punti x di RN in cui queste esistono la v verifica l'e. di Hamilton-Jacobi-Bellman λv(x)+H(x,∇v(x))=0, dove H(x, p)=supa∈A[−f(x, a)∙p−L(x, a)]. Per dare un significato preciso a questa e. si può ricorrere alla nozione di soluzioni di viscosità, che permette inoltre di caratterizzare la funzione valore come unica soluzione di tale equazione. Da queste brevi considerazioni si intuisce l'importanza dei legami tra le soluzioni di viscosità e il campo del controllo ottimo. Naturalmente, l'analisi di questi legami ha portato ad ampliare la teoria in nuove direzioni, quale la possibilità di considerare soluzioni di viscosità discontinue (Bardi, Capuzzo Dolcetta 1997).
Alcuni dei progressi più significativi dovuti alla teoria delle soluzioni di viscosità si sono avuti con l'estensione di questa nozione di soluzione alle e. del secondo ordine
verificanti un'opportuna condizione di ellitticità (anche degenere). Questo sviluppo è stato reso possibile dall'iniziale risultato di unicità di R. Jensen (1988) e quindi dal lavoro di vari altri studiosi (Crandall, Ishii, Lions 1992). La generalizzazione delle soluzioni di viscosità per e. di tipo [7] - conservando proprietà analoghe a quelle descritte nel caso di e. del primo ordine - ha avuto conseguenze notevoli. Da un lato, infatti, essa ha permesso di estendere il metodo della programmazione dinamica al controllo ottimo e ai giochi differenziali stocastici in casi di diffusione degenere (Fleming, Soner 1993). Dall'altro, grazie ai lavori di L.C. Evans e J. Spruck (1991) e di X. Chen, Y. Giga, S. Goto (1991), ha consentito di dare una descrizione rigorosa dell'evoluzione di una superficie secondo la sua curvatura media, importante problema di geometria differenziale che ha applicazione alla descrizione di alcuni fenomeni di transizione di fase (v. geometria: Moto per curvatura media, in questa Appendice). Osserviamo che nessuno dei metodi precedentemente noti era stato in grado di fornire una soluzione valida a quest'ultima questione dopo l'insorgere della prima singolarità. Tra gli sviluppi più recenti della teoria delle soluzioni di viscosità va segnalato lo studio di e. - di tipo [1] e [7] - in dimensione infinita, e cioè nel caso in cui Ω sia un aperto in uno spazio di Hilbert o di Banach (v. funzionale, analisi, App. IV). Una motivazione per questa generalizzazione è rappresentata dalle applicazioni a problemi di controllo ottimo per sistemi che abbiano come e. di stato un'e. alle derivate parziali, per es. l'e. del calore o delle onde (Li, Yong 1995).
bibliografia
R. Courant, D. Hilbert, Methods of mathematical physics, New York 1953.
R. Bellman, Dynamic programming, Princeton 1957.
P.-L. Lions, Generalized solutions of Hamilton-Jacobi equations, Boston 1982.
M.G. Crandall, P.-L. Lions, Viscosity solutions of Hamilton-Jacobi equations, in Transactions of the American mathematical society, 1983, 277, pp. 1-42.
M.G. Crandall, L.C. Evans, P.-L. Lions, Some properties of viscosity solutions of Hamilton-Jacobi equations, in Transactions of the American mathematical society, 1984, 282, pp. 487-502.
H. Ishii, Perron's method for Hamilton-Jacobi equations, in Duke mathematical journal, 1987, pp. 369-84.
R. Jensen, The maximum principle for viscosity solution of second order fully nonlinear partial differential equations, in Archive for rational mechanics and analysis, 1988, 101, pp. 1-27.
X. Chen, Y. Giga, S. Goto, Uniqueness and existence of viscosity solutions of generalized mean curvature flow equations, in Journal of differential geometry, 1991, pp. 749-86.
L.C. Evans, J. Spruck, Motion of level sets by mean curvature, i, in Journal of differential geometry, 1991, pp. 635-81.
M.G. Crandall, H. Ishii, P.-L. Lions, User's guide to viscosity solutions of second order partial differential equations, in Bullettin of the American mathematical society, 1992, pp. 1-67.
W.H. Fleming, H.M. Soner, Controlled Markov processes and viscosity solutions, Berlin 1993.
X. Li, J. Yong, Optimal control theory for infinite dimensionals systems, Boston 1995.
M. Bardi, I. Capuzzo Dolcetta, Optimal control and viscosity solutions of Hamilton-Jacobi-Bellman equations, Boston 1997.
Equazioni di Painlevé
di Hiroshi Umemura
L'interesse per la famiglia delle e. differenziali ordinarie dette di Painlevé è rinato negli ultimi anni, a partire dalla comparsa di una delle funzioni speciali a essa associate, nel 1976, in ricerche dell'ambiente della fisica matematica. Una delle questioni fondamentali che riguardano tali e., l'irriducibilità, era rimasta aperta per più di ottant'anni. Si tratta di un settore di ricerca che fa uso di strumenti della teoria delle funzioni classiche, della teoria delle e. differenziali e di tecniche algebriche. P. Painlevé credeva che la dimostrazione di irriducibilità dipendesse dalla teoria di Galois in dimensione infinita; K. Nishioka e H. Umemura hanno dimostrato che questa congettura non è vera. Anche se costituirebbe uno strumento molto efficace, non esiste ancora una teoria di Galois differenziale in dimensione infinita che sia largamente accettata (Pommaret 1983; Umemura 1996).
Funzioni speciali, equazioni di Painlevé e teoria di Galois differenziale
Così come all'interno dei sistemi numerici alcuni numeri rivestono una particolare importanza rispetto ad altri (per es. il numero π), tra le funzioni ne esistono alcune, dette funzioni speciali, che svolgono un ruolo fondamentale nella matematica pura, in fisica e in ingegneria. Oltre alle funzioni elementari seno, coseno e logaritmo, limitandoci alle funzioni di una variabile si possono citare la funzione gamma, la funzione zeta di Riemann, le funzioni ipergeometriche e le loro confluenti (le quali sono soluzioni di e. differenziali lineari del secondo ordine) e le funzioni ellittiche (v. funzione: Funzioni notevoli, XVI, p. 193). In generale, una funzione può essere definita in molti modi.
a) Definizione tramite un'e. funzionale. Per es., se τ è fissato, la funzione teta ϑ(t, τ), della quale in seguito verrà data l'usuale definizione tramite una serie, è caratterizzata, a meno di una costante moltiplicativa, tramite le e. fun-
zionali ϑ(t+1, τ)=ϑ(t, τ), ϑ(t+τ, τ)=exp(−π −1τ−2π −1t) ϑ(t, τ).
Perciò quando τ è fissato così che la funzione teta ϑ(t, τ) risulti essere funzione di una variabile t, possiamo adottare le e. funzionali di cui sopra come definizione della funzione teta ϑ(t, τ).
b) Definizione tramite un'e. differenziale. Un'e. differenziale è un caso particolare di e. funzionale e quindi questo metodo di definizione rappresenta un caso particolare del metodo precedente. La funzione ℘ di Weierstrass soddisfa un'e. differenziale (dy/dt)²=4y³−g₂y−g₃, dove g₂, g₃ sono costanti; viceversa ogni soluzione y di questa e. differenziale può scriversi come y=℘(t+c), con c ∈ C. Così possiamo dire che l'e. differenziale data caratterizza la funzione ℘ di Weierstrass.
c) Definizione tramite una serie. L'esponenziale expt, la funzione ϑ e la funzione ℘ di Weierstrass sono introdotte di solito tramite la loro espansione in serie. Sono qui di seguito riportate le serie che definiscono rispettivamente queste funzioni:
dove H denota l'insieme dei numeri complessi con parte immaginaria positiva. Per una coppia di numeri complessi w₁, w₂ linearmente indipendenti su R, definiamo la funzione ℘ di Weierstrass nella variabile t come
dove w=mw₁+nw₂ e (m, n) variano, nella sommatoria, su tutte le coppie di interi diverse da (0,0). Sebbene la funzione ℘ di Weierstrass ℘(t; w₁, w₂) dipenda da t, w₁, w₂, qui la studieremo principalmente come funzione di t. La funzione ipergeometrica F(a, b; c; t) è data dalla serie:
d) Definizione tramite rappresentazione integrale e altri metodi. La famosa
rappresentazione integrale Γ(t)=∫₀∞e⁻zzt⁻¹dz può essere considerata come una
definizione della funzione gamma Γ(t), così come la formula di Eulero
Ogni metodo presenta dei vantaggi e degli svantaggi. Per es. una funzione analitica ha un'espansione di Taylor e quindi ogni funzione analitica è data da una serie esplicita; tuttavia, è molto difficile in generale dimostrare proprietà della funzione a partire da una serie data. Le e. differenziali algebriche, che sono della forma
formula 24
(dove F è un polinomio, a coefficienti complessi, in t, y e nelle sue derivate y′ = dy/dt, …, y(n)=dny/dtn), hanno offerto classicamente uno dei metodi ragionevoli e sistematici per definire funzioni. Più precisamente si voleva scoprire una classe di funzioni speciali in una variabile definita tramite e. differenziali algebriche, la quale fosse più ampia rispetto a quella delle funzioni ipergeometriche, delle loro confluenti (le quali sono soluzioni di e. differenziali lineari del secondo ordine) e delle funzioni ellittiche (per es. la funzione di Weierstrass). Ci si occupava di e. differenziali (ordinarie) algebriche non lineari, come quella che soddisfa la funzione di Weierstrass. Invece di imporre la condizione (globale) che le funzioni speciali soddisfacenti l'e. differenziale fossero meromorfe sul piano complesso C, si preferì considerare e. differenziali senza punti singolari movibili, vale a dire tali che non ci siano né punti di ramificazione né punti singolari trascendenti che dipendano da una soluzione. Questa proprietà è detta proprietà di Painlevé.
Si consideri per es. l'e. differenziale algebrica 2yy′=1. La soluzione generale è y(c, t)= t−c, dove c ∈ C è una costante di integrazione. La soluzione y(c, t) è parametrizzata da c ∈ C e t=c è il punto di ramificazione della soluzione y(c, t). Perciò al variare di c il punto di ramificazione t=c varia dipendendo dalla soluzione y(c, t). Quindi l'e. differenziale 2yy′=1 ha un punto singolare movibile.
A partire dal caso più facile n=1 e proseguendo per n=2, 3, …, ci si aspettava di incontrare molte funzioni speciali. L. Fuchs e H. Poincaré dimostrarono nel 1884 che nel caso n=1, se un'e. differenziale algebrica non ha punti singolari movibili essa può essere integrata tramite funzioni già note e quindi tale e. non definisce nessuna nuova funzione. Perciò, allo scopo di scoprire nuove funzioni speciali, si studiò il caso n≥2. Dopo alcuni tentativi, E. Picard, che aveva proposto questo problema per n=2, rinunciò a scoprire nuove funzioni speciali seguendo questa via perché, secondo lui, era praticamente impossibile decidere se un'e. differenziale algebrica avesse o meno punti singolari movibili senza scrivere esplicitamente le soluzioni. Painlevé riuscì a determinare delle e. differenziali algebriche y″=R(t,y,y′) che non avevano punti singolari movibili, dove R(t,y,y′) è una funzione razionale di t, y, y′. Quindi egli scartò quelle e. che poteva integrare tramite funzioni già note e, intorno al 1900, ottenne le prime tre famiglie PI, PII, PIII delle sei e. di Painlevé.
Nella prefazione alle opere complete di Painlevé (1972), Garnier ricorda le parole di Poincaré il quale, quando vide Painlevé inaugurare la serie dei suoi lavori, avrebbe voluto dirgli: "Fermatevi, voi vi impegnate in una via che conduce a un muro insuperabile"; ma dopo aver visto i risultati ottenuti affermò: "Questo muro, tramite uno sforzo mirabile e prodigioso, egli [Painlevé] è riuscito a superarlo, e il suo trionfo è uno dei più belli della scienza francese". Com'è evidente dalle motivazioni della ricerca, ci si aspettava che fosse impossibile integrare le e. di Painlevé tramite le funzioni già note, e cioè che le e. di Painlevé fossero irriducibili alle funzioni conosciute. La carriera di Painlevé come matematico fu dedicata proprio a questo problema. Nel 1895 egli fu invitato dall'Accademia di Stoccolma, dove presentò la sua ricerca con una serie di lezioni (note come lezioni di Stoccolma) nelle quali introduceva induttivamente l'insieme delle funzioni note fino ad allora e dimostrava l'irriducibilità di certe e. differenziali algebriche del tipo [1] per n=2. Nel 1902, Painlevé annunciò l'irriducibilità della prima e. di Painlevé y″=6y²+t sui Comptes rendus dell'Accademia delle scienze di Parigi. R. Liouville non accettò la sua tesi, sostenendo che la prima e. di Painlevé era riducibile a un'e. differenziale lineare del quarto ordine con coefficienti algebrici, e iniziò una controversia dai toni aspri sui Comptes rendus. Il fatto che venissero pubblicati i risultati senza dimostrazioni dettagliate non aiutò a dirimere la questione. Painlevé scriveva in una delle sue note: "Il signor Liouville non ha che la scelta tra un truismo (evidente per qualsivoglia equazione differenziale) o un errore". Al che Liouville replicava: "L'errore che mi è stato rimproverato non è mio e la mia Nota citata non lascia nessun dubbio, né alcuna scelta da fare. Per quanto riguarda la proposizione che il signor Painlevé sembra oggi considerare come un truismo, essa si trova nella sua Nota dell'8 settembre".
Nel corso della controversia Painlevé lasciò da parte l'approccio contenuto nelle lezioni di Stoccolma, e preferì basare la dimostrazione d'irriducibilità su una teoria generale per le e. differenziali che fosse analoga alla teoria di Galois per le e. algebriche (v. algebra, II, pp. 438-39). Si noti infatti la somiglianza del problema della risolubilità delle e. algebriche con quello dell'irriducibilità delle e. di Painlevé. Entrambi affermano l'impossibilità di risolvere e.: le e. algebriche tramite operazioni ammissibili (estrazione di radicali e le quattro operazioni dell'aritmetica) nel primo caso, e le e. differenziali tramite le funzioni note (fino ad allora) nel secondo caso. S. Lie progettava di applicare alle e. differenziali la produttiva idea di Galois e Abel per la teoria delle e. algebriche, e Picard stabilì una teoria di Galois per le e. differenziali lineari ordinarie (v. equazioni, XIV, p. 140 e p. 145). La teoria di Picard, che attualmente è chiamata teoria di Picard-Vessiot, è finito-dimensionale, mentre il programma di Lie è essenzialmente infinito-dimensionale.
Nel 1898, J. Drach presentò nella sua tesi di dottorato il primo tentativo di sviluppare una teoria di Galois per le e. differenziali in dimensione infinita. Esaminando questo lavoro Vessiot trovò diverse lacune nelle definizioni e nelle dimostrazioni, e lo comunicò a Painlevé. Ciononostante quest'ultimo decise di ricorrere alla teoria di Drach per ottenere una dimostrazione dell'irriducibilità, forse perché aveva trovato gravi difficoltà a fornire una tale dimostrazione o perché credeva che le lacune del lavoro di Drach potessero essere colmate facilmente. Nella nota con la quale chiuse la controversia con Liouville, Painlevé affermava, in sintesi, che non soltanto l'e. PI è irriducibile a un'e. differenziale lineare d'ordine quattro con coefficienti algebrici (punto di partenza della discussione), ma che essa è anche irriducibile in un senso più generale. Inoltre egli si mostrava convinto del fatto che potevano essere dati fondamenti rigorosi alla teoria di Drach e che essa avrebbe fornito una dimostrazione convincente del teorema generale di irriducibilità. Egli scriveva nel 1902: "Detto in altro modo, una equazione irriducibile, nel senso di Drach, non può essere attaccabile tramite alcun procedimento di integrazione formale. [...] Non ignoro affatto quello che una tale affermazione sembra avere di audace e di paradossale. È una verità portante ed è questo punto che mostra la potenza e la generalità del teorema di Drach [...]. È possibile che la mia opinione riguardo a questo argomento sia "un po' isolata", come dice il signor Liouville. Ma questa sarà ben presto l'opinione unanime quando il teorema di Drach, avendo ricevuto un'esposizione didattica e definitiva, sarà divenuto familiare ai geometri" (Painlevé 1972). La sua opinione era troppo ottimistica. Anche Vessiot impiegò tutta la vita per stabilire la teoria di Galois differenziale in dimensione infinita, ma la teoria non fu mai così chiara come Painlevé si aspettava, né fu accettata dal pubblico. Drach diede nel 1915 una dimostrazione non corretta dell'irriducibilità della prima e. di Painlevé che dipendeva dalla sua incompleta teoria di Galois.
Seguendo un'idea di B. Riemann, R. Fuchs, matematico tedesco, figlio di L. Fuchs, studiò le deformazioni che conservavano la monodromia di un'e. differenziale lineare ordinaria e, nel 1907, scoprì la sesta e. di Painlevé PVI, la quale non compariva nella tavola di Painlevé. La tavola essendosi rivelata incompleta, Painlevé fu costretto a rivedere il risultato con il suo studente Gambier. Nel 1910 essi arrivarono alla lista completa delle sei famiglie PI, PII, …, PVI delle equazioni di Painlevé:
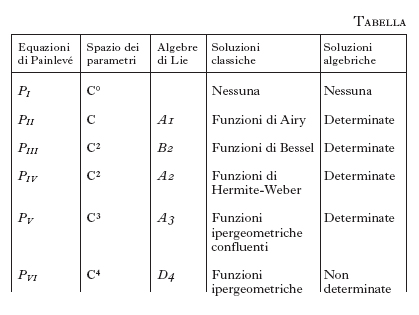
dove α, β, γ, δ sono parametri complessi. In PIII si può assumere γ=4, δ=-4 e in PV si può assumere che δ=-1/2. In tal modo risulta che PII, PIII, PIV, PV, PVI dipendono rispettivamente da uno, due, due, tre, quattro parametri (v. tab.).
La definizione di funzione classica
La prima cosa da fare per dimostrare l'irriducibilità è proprio dare una definizione matematica di 'funzione nota'. Negli anni Ottanta Umemura ha sviluppato la teoria delle funzioni classiche ispirata alle lezioni di Stoccolma di Painlevé e basata sulla teoria di Galois differenziale (finito dimensionale) sviluppata da E. Kolchin. In quel che segue studieremo insiemi di funzioni meromorfe su un dominio di C. Denotiamo le coordinate di C, cioè la variabile indipendente, tramite t. Sia f una funzione meromorfa su un dominio complesso D. Diremo che la restrizione f|D′ di f a un sottodominio D′ ⊂ D è una funzione nota se e solo se f è una funzione nota. Analizzando le lezioni di Stoccolma possiamo estrarre le seguenti 'operazioni ammissibili' per generare funzioni note.
(O)-Se f(t) è una funzione nota allora la derivata f′(t) è una nuova funzione nota.
(P1)-Se f(t), g(t) sono funzioni note allora la somma f(t)+g(t), la differenza f(t)−g(t), il prodotto f(t)g(t), e inoltre il quoziente f(t)/g(t) (se g(t)≠0) sono funzioni note.
(P2)-Siano a₁(t), a₂(t), …, an(t) funzioni note. Allora una soluzione f(t) dell'e. algebrica f(t)n+a₁(t)f(t)n⁻¹+…+an(t)=0 è una nuova funzione nota.
(P3)-Sia f(t) una funzione nota. Una soluzione F(t) di un'e. differenziale F′(t)=f(t) è una nuova funzione nota. Detto in altre parole, la quadratura di una funzione nota è una funzione nota.
(P4)-Siano a₁(t), a₂(t), …, an(t) funzioni note. Allora una soluzione f(t) dell'e. differenziale f(t)(n)+a₁(t)f(t)(n⁻¹)+…+an(t)=0 è una nuova funzione nota.
(P5)-Sia A una varietà abeliana su C di dimensione n e p: Cn→A la mappa di ricoprimento universale. Siano a₁(t), a₂(t), …, an(t) funzioni note meromorfe su un dominio complesso D. Possiamo considerare la funzione meromorfa F:D→Cn, tU(a₁(t), a₂(t), …, an(t)). Allora per ogni funzione razionale f sulla varietà abeliana A (così che f o p:Cn→A→C è una funzione abeliana per definizione) la funzione composta f o p o F è una nuova funzione nota. In altre parole possiamo sostituire funzioni note in una funzione abeliana per ottenere nuove funzioni note.
Il seguente esempio illustra l'operazione (P5). Siano w₁, w₂ numeri complessi linearmente indipendenti su R. Poniamo L=Zw₁+Zw₂. L è un sottogruppo del gruppo additivo C dei numeri complessi e quindi A:=C/L è una curva ellittica o una varietà abeliana di dimensione uno. Consideriamo la mappa di ricoprimento universale p:C→C/L. La funzione ℘ di Weierstrass ℘ (x; w₁, w₂) è una funzione meromorfa su C tale che ℘ (x+w; w₁, w₂)= ℘ (x; w₁, w₂) per ogni w ∈ L. Perciò esiste una funzione razionale f sulla curva ellittica A tale che p o f=℘ (x; w₁, w₂), cioè ℘ (x; w₁, w₂) è una funzione abeliana. L'operazione (P5) in questo caso particolare dice che possiamo sostituire un'arbitraria funzione nota a(t) nella funzione ℘ di Weierstrass ℘ (x; w₁, w₂) per ottenere una nuova funzione nota ℘ (a(t); w₁, w₂).
Queste operazioni non sono indipendenti, in quanto le operazioni (P2) e (P3) sono combinazioni delle operazioni (O), (P1), (P4). Di conseguenza, se possiamo risolvere e. differenziali lineari allora possiamo risolvere anche e. algebriche. A questo punto si pone in modo naturale la questione se tali operazioni, che ci sono suggerite dall'esperienza, siano ragionevoli o se abbiano un qualche significato teorico. Per es., nel problema della soluzione di un'e. algebrica per radicali le operazioni ammissibili che l'esperienza ci suggerisce sono l'addizione, la sottrazione, la moltiplicazione, la divisione e l'estrazione di radicali: la teoria di Galois mostra che queste operazioni per le e. algebriche sono equivalenti al consentire le estensioni cicliche dei campi, per cui esse hanno significato teorico. Ci si può aspettare che anche nel nostro caso esista una caratterizzazione teorica di queste sei operazioni? In effetti esse possono essere ridotte a una semplice operazione relativa ai gruppi algebrici.
Sia D ⊂ C un dominio complesso. Consideriamo una funzione olomorfa F:D→GLn, tU(F(t)i,j)₁≤i,j≤n, dove GLn è il gruppo delle matrici regolari n×n. Assumiamo che le entrate della derivata logaritmica F′F⁻¹ (denotata da lδF), la quale è una matrice n×n, siano funzioni note. Allora possiamo risolvere un'e. lineare F′=AF tramite le operazioni ammissibili, dove denotiamo con A la derivata logaritmica lδF=F′F⁻¹ (notiamo qui che possiamo considerare la derivata logaritmica lδF come una mappa olomorfa D→gln, dove gln è l'algebra di Lie GLn, vale a dire gln è l'algebra di Lie Mn delle matrici n×n). Possiamo ricostruire tramite le operazioni ammissibili la funzione olomorfa F:D→GLn quando la derivata logaritmica lδF:D→gln è nota. Per generalizzare questa operazione a un qualsiasi gruppo algebrico, consideriamo una funzione olomorfa F:D→G da un dominio complesso D a un gruppo algebrico G. Possiamo definire la derivata logaritmica lδF:D→g, dove g è l'algebra di Lie del gruppo algebrico G (g è uno spazio vettoriale di dimensione d, dove d è la dimensione del gruppo algebrico G). Introduciamo la seguente operazione:
(Q)-sia F:D→G una mappa olomorfa da un dominio complesso D a un gruppo algebrico G, se la derivata logaritmica lδF:D→g≃Cd, tU(f₁(t), f₂(t),…, fd (t)) è data dalle funzioni note fi(t) per 1≤i≤d allora possiamo ricostruire la funzione olomorfa F.
Si ha il seguente risultato. Sia S un insieme di funzioni meromorfe su un dominio complesso D. Allora per una funzione olomorfa f su un sottodominio di D le seguenti condizioni sono equivalenti:
(1)-f si ottiene da S tramite un'iterazione finita delle operazioni ammissibili (O), (P1), (P2), …, (P5);
(2)-f si ottiene da S tramite un'iterazione finita delle operazioni (O), (P1), (Q).
Studiamo l'insieme delle operazioni (O), (P1). Sia D un dominio complesso e consideriamo un insieme S di funzioni meromorfe su D. Poiché abbiamo l'operazione (P1), possiamo assumere che S sia chiuso rispetto all'addizione, alla sottrazione, alla moltiplicazione e alla divisione, e cioè che l'insieme S sia un campo. Abbiamo inoltre l'operazione (O) per cui possiamo assumere che il campo S sia chiuso rispetto alla derivazione. Questo significa che S è un campo differenziale. Torniamo ora alla funzione olomorfa F:D→G tale che la derivata logaritmica lδF:D→g,tU(f₁(t), f(t), …, fd(t)) sia data da funzioni note fi(t) per 1≤i≤d. Assumiamo che le fi(t) appartengano a un campo differenziale K di funzioni note meromorfe su D. Aggiungendo al campo K le funzioni ottenute tramite l'operazione (Q) otteniamo un'estensione di campo differenziale L/K. Kolchin ha chiamato questo tipo di estensione di campo differenziale estensione G-primitiva. A meno di estensioni algebriche finite, un'estensione G-primitiva è equivalente a un'estensione fortemente normale, la quale è la controparte differenziale, nella teoria di Galois differenziale elaborata da Kolchin, di un'estensione di Galois. In questo modo, si ha il seguente risultato che rende chiaro il significato teorico delle operazioni ammissibili introdotte all'inizio. Se partiamo da un campo differenziale di funzioni note, allora ammettere un numero finito di iterazioni delle operazioni ammissibili (O), (P1), (P2), …, (P5) è equivalente a permettere estensioni successive G-primitive del campo differenziale di partenza.
Definiamo ora induttivamente le funzioni classiche come segue. Si parte dal campo C(t) delle funzioni razionali e si applicano le operazioni ammissibili (O), (P1), (P2), …, (P5) per ottenere le funzioni classiche. Secondo questa definizione, i polinomi, le funzioni razionali, più generalmente le funzioni algebriche, expt, logt, le funzioni ipergeometriche e le loro confluenti e le funzioni ellittiche sono classiche. Quindi tutte le funzioni speciali descritte nel classico manuale di E.T. Whittaker e G.N. Watson (1927) in relazione con le e. differenziali sono classiche, tranne la funzione gamma, la quale non soddisfa nessuna e. differenziale algebrica con coefficienti in C(t).
Esempio 1. Se si considerano a₁(t), a₂(t) funzioni classiche arbitrarie, ogni funzione che soddisfa un'e. differenziale lineare non omogenea
è una funzione classica. Infatti se a₂=0 allora f è classica per (P4). Se a₂≠0 allora poniamo f=uy, dove y è una soluzione di y′+a₁y=0. In questo modo y è classica per (P4). Sostituendo f=uy nell'e. otteniamo u′=−a₂/y e quindi u è classica per (P3). Perciò f è classica per (P1).
Esempio 2. Consideriamo una funzione f(t) che soddisfa l'e. di Riccati f′(t)+a₀(t)f(t)²+a₁(t)f(t)+a₂=0 dove le ai(t) (0≤i≤2) sono classiche. Allora f(t) è classica. Infatti, se a₀=0 allora f è classica per l'esempio precedente. Se a₀≠0 allora sostituendo f con f/a₀, se necessario, possiamo supporre a₀=1. Ora se poniamo f(t)=y′(t)/y(t), allora y è una soluzione di un'e. differenziale lineare omogenea y″(t)+a₁(t)y′(t)+a₂(t)y(t)=0. Perciò y è classica per (P4) e di conseguenza f=y′/y è classica per (O) e (P1).
Le funzioni classiche sono chiuse rispetto alla sostituzione. Questo vuol dire che possiamo dimostrare per induzione il seguente teorema. Sia fi(t) una funzione meromorfa classica su un dominio complesso Di (per i=1, 2). Se f₁(D₁) ⊂ D₂ e se l'immagine f₁(D₁) non è contenuta nell'insieme dei poli di f₂ così che è definita la funzione meromorfa f₂ o f₁:D₂→D₁→C, allora f₂ o f₁ è una funzione classica.
Dimostrazione dell'irriducibilità delle equazioni di Painlevé
Le e. di Painlevé furono quasi dimenticate fino a quando i fisici matematici non si imbatterono in una di tali e. nel 1976. Essi furono sorpresi nell'apprendere che i matematici conoscevano già all'inizio del secolo tali funzioni speciali e che le avevano dimenticate. Nessuno dubitava che l'irriducibilità fosse una delle questioni fondamentali delle e. di Painlevé, ma dopo la controversia con Liouville il problema dell'irriducibilità non era stato affrontato per più di ottant'anni, a parte la dimostrazione non corretta di Drach nel 1915.
Alcuni credevano che Painlevé avesse dimostrato l'irriducibilità della prima e., ma altri erano sospettosi. In quei giorni ci si trovava persi nella inusuale disputa matematica tra Painlevé e Liouville. Le seguenti parole di J. Favard nel suo corso di analisi presso la Scuola normale superiore di Parigi nel 1962 descrivono bene l'atmosfera: "Dunque l'integrazione non sembra possibile per mezzo delle funzioni che noi conosciamo. In effetti, senza che noi si possa dare dei dettagli, si mostra che gli integrali di queste equazioni sono delle funzioni nuove, in un senso che non possiamo pensare di precisare".
Nel 1987 K. Nishioka diede un contributo essenziale per dimostrare l'irriducibilità della prima e. di Painlevé. Umemura analizzò il risultato di Nishioka e combinò il suo argomento con la teoria delle funzioni classiche, che era stata sviluppata precedentemente. Avendo definito rigorosamente le funzioni classiche possiamo infatti descrivere con un'asserzione precisa cosa si intende dicendo che la prima e. di Painlevé è irriducibile: nessuna soluzione della prima e. di Painlevé è classica. La dimostrazione di questo teorema dà come corollario il risultato che pone fine alla controversia intercorsa tra Painlevé e Liouville: nessuna soluzione della prima e. di Painlevé è riducibile a un'e. differenziale lineare i cui coefficienti siano funzioni algebriche. Più precisamente, siano aij(t) (1≤i, j≤n) funzioni algebriche e consideriamo un'e. differenziale lineare Y′(t)=A(t)Y(t) con detY(t)≠0, dove A(t)=(aij(t))₁≤i,j≤n e Y(t)=(yi,j(t))₁≤i,j≤n sono matrici n×n: si può mostrare che nessuna soluzione della prima e. di Painlevé è contenuta nel campo differenziale C(t,aij(t), yi,j(t))₁≤i,j≤n. Sebbene non sia evidente dalla sua origine, il problema dell'irriducibilità della prima e. di Painlevé è di natura algebrica. Perciò per ottenere la dimostrazione di questi risultati bisogna lavorare nel campo dell'algebra astratta.
Sia K un'estensione del campo differenziale (C(t), d/dt) delle funzioni razionali. Questo significa che K è un'estensione di campo di C(t) e inoltre esiste una derivazione δ:K→K tale che δ è un'estensione della derivazione d/dt:C(t)→C(t) così che abbiamo δ(a+b)=δ(a)+δ(b), δ(ab)=δ(a)b+aδ(b) per ogni a, b ∈ K. Siano Y, Y′ variabili su K. Introduciamo una derivazione XI: = δK + Y′∙/∙Y + (6Y² + t) ∙/∙Y′:K[Y, Y′]→K[Y, Y′]. Qui il primo termine δK denota, per abuso di notazione, la derivazione di K[Y, Y′] ottenuta applicando la derivazione δK del campo differenziale (K, δ) ai coefficienti dei polinomi. Questo significa che se F(Y, Y′)=ΣaijYiY′j ∈ K[Y, Y′], dove aij ∈ K, allora δK(F(Y,Y′)): =ΣδK(aij) yiyij ∈ K[Y, Y′]. Così, in particolare, se l'estensione di campo differenziale K coincide con C(t), allora XI non è nient'altro che ∙/∙t+Y′∙/∙Y+(6Y²+t)∙/∙Y′. Il punto cruciale è la seguente condizione universale. Sia K un'estensione di campo differenziale di C(t). Diciamo che un polinomio F(Y, Y′) ∈ K[Y, Y′] è XI-invariante se esiste un polinomio G(Y, Y′) ∈ K[Y, Y′] tale che si abbia XI(F(Y, Y′))=G(Y, Y′)F(Y, Y′). Una funzione costante F(Y, Y′)=c ∈ K ⊂ K[Y, Y′] è evidentemente XI-invariante. Un tale polinomio XI-invariante viene detto banale. È conveniente introdurre la seguente condizione (J) su XI: diremo che una derivazione XI soddisfa tale condizione se per ogni K estensione di campo differenziale di C(t), non esiste nessun polinomio non banale XI-invariante in K[Y, Y′].
Si verifica infatti che la derivazione XI soddisfa la condizione (J), da cui otteniamo la seguente conclusione: se la prima e. di Painlevé y″=6y²+t ha una soluzione classica η(t), allora η(t) è una funzione algebrica. Questo significa che η(t) soddisfa un'e. algebrica a₀(t)η(t)n+a₁(t)η(t)n⁻¹+…+an(t)=0 nella quale le grandezze ai(t)(0≤i≤n) sono polinomi (tali soluzioni sono dette soluzioni algebriche). Siccome è possibile dimostrare che la prima e. di Painlevé non ha soluzioni algebriche, ne segue che nessuna soluzione della prima e. di Painlevé è classica.
Come abbiamo visto sopra, abbiamo un formalismo per il quale, se una derivazione soddisfa la condizione (J), allora questo implica l'irriducibilità della prima e. di Painlevé a meno di soluzioni algebriche. A partire da questo, la non esistenza di soluzioni algebriche porta al risultato desiderato. Possiamo applicare questo metodo alle altre e. di Painlevé PJ (ii≤J≤vi) che presentano parametri vettoriali v, sostituendo la derivazione XI con la corrispondente derivazione hamiltoniana XJ(v), la quale dipende dai parametri v. Se la derivazione hamiltoniana XJ(v) soddisfa la condizione (J) per un certo valore v dei parametri, allora il formalismo generale implica che per questo valore v dei parametri nessuna soluzione dell'e. di Painlevé PJ è classica, eccetto che per le soluzioni algebriche. È noto che l'e. di Painlevé PJ è equivalente al sistema
dove HJ=HJ(v, t, q, p) è una funzione razionale di t, q, p e di un vettore v che parametrizza il sistema SJ(v), tale che HJ(v, t, q, p) è un polinomio di q, p e v (i≤J≤vi). Questo significa che SJ(v) (detto sistema di Painlevé parametrizzato da v) è un sistema hamiltoniano con hamiltoniana HJ.
La prima e. di Painlevé, per es., non contiene parametri. Poniamo HI(t, q, p)=(1/2)p²−2q³−qt così che
Possiamo controllare che q soddisfa la prima e. di Painlevé q″=6q²+t se eliminiamo p dal sistema SI. La seconda e. di Painlevé PII(α):y″=2y³+ty+α contiene un parametro α. Così il parametro v appartiene a uno spazio vettoriale di dimensione uno e quindi possiamo denotarlo con v, cioè con un numero complesso. Poniamo HII(v, t, q, p)=1/2p²−(q²+t/2)p−qv. Perciò
Il sistema SII(v) è equivalente a PII(α), dove v e α soddisfano l'uguaglianza v=α+1/2. Infatti se eliminiamo p dal sistema SII(v), q soddisfa la seconda e. di Painlevé PII(α) q″=2q³+tq+v−1/2 con α=v−1/2.
Da adesso in poi, studiamo il sistema di Painlevé SJ(v) per l'e. di Painlevé PJ. L'e. di Painlevé PJ ha soluzioni classiche per ii≤J≤vi e per valori particolari dei parametri. Infatti le funzioni ipergeometriche, le funzioni ipergeometriche confluenti, le funzioni di Hermite-Weber, le funzioni di Bessel e le funzioni di Airy sono implicate rispettivamente in PVI, PV, PIV, PIII e PII. Queste soluzioni classiche degenerano in soluzioni algebriche (v. tab.). Per es., se la funzione di Hermite-Weber degenera in un polinomio di Hermite otteniamo una soluzione razionale di PIV. Inoltre abbiamo anche soluzioni algebriche che non sono riducibili alla serie di soluzioni classiche descritte sopra.
Se v=0 allora il sistema SII(v) diventa
Se consideriamo una soluzione di una e. di Riccati q′=−q²−t/2 allora (q, 0) è una soluzione classica di SII(0) per l'esempio 2 visto in precedenza. In effetti se poniamo q=y′/y allora l'e. di Riccati viene linearizzata all'e. di Airy y″+(1/2)ty=0. Così q=y′/y è una soluzione classica, la quale è espressa in termini della funzione di Airy y, della seconda e. di Painlevé PII(α)q″=2q³+tq+α per α=−1/2. Poiché la funzione di Airy contiene due parametri, il quoziente q=y′/y ha un parametro così che q=y′/y è una famiglia a un parametro di soluzioni classiche della seconda e. di Painlevé PII(α). Se v=1/2 allora abbiamo
Quindi (q, p)=(0, t/2) è una soluzione di SII(1/2) o, in modo equivalente, y=0 è una soluzione razionale di PII(α)y
″=2y³+ty+α per α=0.
A questo punto è opportuno dare una definizione precisa. Denotiamo con P una delle seguenti proprietà della funzione f: (i) f è una funzione razionale; (ii) f è una funzione algebrica; (iii) f è una soluzione classica. Per un intero J con i≤J≤vi, sia (q, p) una soluzione del sistema SJ(v). Diciamo che la soluzione (q, p) ha la proprietà P se sia q che p hanno la proprietà P. La soluzione (q, p) viene detta trascendente se non è algebrica (cioè se una delle due non è algebrica). Determinare l'irriducibilità delle e. di Painlevé vuol dire, secondo questo approccio, determinare le soluzioni classiche delle e. di Painlevé.
Per la prima e. di Painlevé abbiamo considerato la derivazione XI=δK+Y′∙/∙Y−(6Y²+t)∙/∙Y′:K[Y, Y′]→K[Y, Y′] per un campo differenziale K estensione di C(t), dove Y e Y′ sono variabili su K tali che K[Y, Y′] è un anello di polinomi. Da quanto si è visto per la seconda e. di Painlevé, la derivazione corrispondente per SII è
∙ ∙
la quale è una derivazione per l'anello di polinomi K[Q, P], dove K è un campo differenziale estensione di C(t), e Q, P sono variabili su K. In generale la derivazione corrispondente per SJ(v) è
la quale è una derivazione per l'anello di polinomi K[Q,P] per un campo differenziale K estensione di C(t) (i≤J≤vi). Definiamo in modo simile un polinomio XJ-invariante così come una condizione (J) relativa alla derivazione XJ, a partire dalla quale otteniamo una conclusione analoga a quella prima descritta per la prima e. di Painlevé: sia J un intero tale che i≤J≤vi; se per un particolare valore v dei parametri la derivazione XJ(v) soddisfa la condizione (J), allora nessuna soluzione del sistema SJ(v) è classica se si escludono le soluzioni algebriche.
Per illustrare il caso generale, applichiamo questo risultato alla seconda e. di Painlevé. Si può dimostrare che se la derivazione XII(v) non soddisfa la condizione (J) allora v è un intero. Da questo deriva il seguente corollario: se v non è intero allora SII(v), e quindi PII(v−1/2), non ha soluzioni classiche se si escludono le soluzioni algebriche. Dobbiamo risolvere ora due problemi: a) che succede quando v ∈ Z?; b) come si determinano le soluzioni algebriche di SII(v) per v ∈ C?
Per quanto riguarda il primo problema, la determinazione dei polinomi X(v)-invarianti per v ∈ Z dà il seguente risultato. Se v=α+1/2 ∈ Z, allora la seconda e. di Painlevé PII(α):y″=2y³+ty+α ha come soluzione classica unicamente la famiglia a un parametro espressa razionalmente dalla funzione di Airy e dalla sua derivata. Eccetto per questo tipo di soluzioni, una soluzione classica dell'e. di Painlevé è algebrica. Quindi per affrontare il problema dell'irriducibilità della seconda e. di Painlevé o per determinare le sue soluzioni classiche non resta che determinare le soluzioni algebriche. Lo studio delle soluzioni algebriche delle e. di Painlevé, che ha un interesse di per sé, ha una lunga storia. Se consideriamo come esempio tipico la seconda e. di Painlevé PII(α) è noto che abbiamo l'unica soluzione razionale PII(n) per ogni intero n ∈ Z e che non c'è nessuna soluzione algebrica a parte queste soluzioni razionali. Perciò il problema dell'irriducibilità della seconda e. di Painlevé è risolto.
Riassumendo, possiamo determinare le soluzioni classiche della seconda e. di Painlevé PII(α) come segue:
(1)-PII(α) ha un'unica soluzione razionale se il parametro α assume un valore intero, cioè se α ∈ Z.
(2)-PII(α) ha come soluzione classica unicamente la famiglia a un parametro espressa razionalmente dalla funzione di Airy e dalla sua derivata se α−1/2 è un intero, cioè se α∈1/2+Z.
(3)-A parte le soluzioni in (1) e (2), nessuna soluzione della seconda e. di Painlevé PII è classica.
Per ragioni tecniche, la determinazione delle soluzioni classiche della seconda e. di Painlevé è divisa in due parti: 1) la determinazione dei polinomi XII(v)-invarianti o determinazione delle soluzioni classiche trascendenti; 2) la determinazione delle soluzioni algebriche. Possiamo applicare questo metodo a tutte le e. di Painlevé. Le soluzioni classiche trascendenti dell'e. di Painlevé PJ sono indicate nella quarta colonna della tabella (i≤J≤vi). Per quanto riguarda le soluzioni algebriche, esse sono determinate se i≤J≤v. In altre parole, nessuna soluzione delle e. di Painlevé è classica eccetto quelle elencate nella quarta e quinta colonna della tabella. La sesta e. di Painlevé risulta non determinata in relazione all'elevato numero di soluzioni algebriche. Il problema rimasto aperto è, pertanto, quello di classificare le soluzioni algebriche della sesta e. di Painlevé.
Le e. di Painlevé hanno gruppi di trasformazione che sono gruppi di Weyl affini. Nella terza colonna della tabella indichiamo il tipo della corrispondente algebra di Lie. Non abbiamo nessuna ragione teorica che spieghi perché incontriamo qui i gruppi di Weyl affini. Possiamo aspettarci una definizione in termini di teoria dei gruppi delle e. di Painlevé tramite le algebre di Lie.
Funzioni classiche ed equazioni di Painlevé
Le e. di Painlevé gettano luce sul rapporto che intercorre fra (i) le funzioni ipergeometriche (e le loro confluenti) e (ii) le funzioni ellittiche. Già alla fine del 18° sec. Gauss aveva scoperto che queste due famiglie di funzioni si trovano in una profonda relazione reciproca. Illustriamo la sua idea tramite un semplice esempio. La serie ipergeometrica F(a, b; c; t) è una soluzione dell'e. differenziale ipergeometrica
dove a, b, c sono parametri complessi. D'altro lato, se consideriamo una famiglia di curve ellittiche y²=z(1−z)(1−tz) parametrizzate da t∈C, allora il periodo
è una soluzione dell'e. differenziale ipergeometrica (I.G.) per a=b=1/2, c=1. Gauss dava molta importanza a questa relazione e alla sua scoperta che le forme modulari sono nascoste nelle medie aritmetico-geometriche. Egli aveva in progetto di scrivere un monumentale articolo sulle medie aritmetico-geometriche, sulle funzioni ellittiche e sulle funzioni ipergeometriche, ma non poté realizzarlo. Le e. di Painlevé, tuttavia, ci offrono un punto di vista completamente differente da quello di Gauss e mostrano un rapporto più diretto fra le due famiglie di funzioni.
Per quel che riguarda le funzioni ellittiche, la prima e. di Painlevé PI:y″=6y²+t è equivalente a y″=6y²+at−g₂/2 tramite la trasformazione (t, y)U(at−g₂/2, y/a²), dove a≠0 e g₂ sono numeri complessi. Ponendo a=0, otteniamo y″=6y²−g₂/2, e. differenziale che è integrata tramite la funzione ℘ di Weierstrass, la quale è una funzione ellittica. In altre parole, la funzione ℘ di Weierstrass è una degenerazione delle prime funzioni di Painlevé (vale a dire, le funzioni che sono definite dalla prima e. di Painlevé). Come abbiamo mostrato nella sezione precedente, la funzione ipergeometrica e le sue confluenti appaiono nelle e. di Painlevé. Così abbiamo un
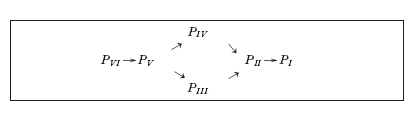
Inoltre, com'è ben noto, abbiamo il seguente diagramma di confluenza delle e. differenziali lineari ipergeometriche:
dove una freccia A→B significa che B è una degenerazione di A. Abbiamo anche i diagrammi di degenerazione delle e. di Painlevé. La sesta e. è la più generale e le altre sono degenerazioni successive alla sesta.
Non solo la funzione ipergeometrica e le sue confluenti appaiono nelle e. di Painlevé: questi due diagrammi di degenerazione sono compatibili. Tradizionalmente le due famiglie (i) e (ii) sono studiate indipendentemente. Le e. di Painlevé ci permettono di trattarle in uno schema di riferimento unico. Perciò le e. di Painlevé non sono pure e semplici generalizzazioni delle due famiglie (i) e (ii), ma queste due famiglie sono collegate con le e. di Painlevé e sono meglio comprese nel contesto della presente teoria.
Abbiamo visto che ci sono due origini per le e. di Painlevé. E cioè: i) l'e. differenziale algebrica [1] per n=2 senza punti singolari mobili; ii) le deformazioni che preservano la monodromia di una e. differenziale lineare. Questi due ingredienti hanno una generalizzazione. In particolare per il secondo punto si è sviluppata una teoria generale feconda, nella quale lo schema sopra descritto, in cui le e. di Painlevé implicano sia le funzioni ipergeometriche e le loro confluenti sia le funzioni ellittiche, ammette una generalizzazione.
Osserviamo infine che, quando ci limitiamo alle e. differenziali algebriche, la funzione gamma Γ(t), la quale non soddisfa nessuna e. differenziale algebrica non banale, è fuori dal nostro schema. Possiamo, tuttavia, migliorare la situazione se nella definizione delle funzioni classiche partiamo dal campo differenziale C(t, Γ(t), Γ′(t),…) invece che dal campo differenziale C(t) delle funzioni razionali, e generiamo funzioni tramite le stesse operazioni ammissibili (O), (P1), (P2), …, (P5) per ottenere il campo differenziale delle funzioni Γ-classiche. Allora tutti i teoremi di irriducibilità continuano a valere a patto di sostituire il termine funzione classica con quello di funzione Γ-classica.
bibliografia
H. Poincaré, Sur un théorème de M. Fuchs, in Acta Mathematica, 1885, 7, pp. 1-32.
J. Drach, Essai sur une théorie générale de l'intégration et sur la classification des transcendentes, in École Normale Supérieure, Annales scientifiques, 1898, 3, pp. 234-384.
E. Vessiot, Sur la théorie de Galois et ses diverses généralisations, in École Normale Supérieure, Annales scientifiques, 1904, 3, pp. 9-85.
J. Drach, Sur le groupe de rationalité des équations du second ordre de M. Painlevé, in Bulletin des sciences mathématiques, 1915, 2, pp. 967-1000.
E.T. Whittaker, G.N. Watson, A course of modern analysis, Cambridge 1927.
E. Kolchin, Differential algebra and algebraic groups, New York-London 1972.
P. Painlevé, Œuvres, Paris 1972; J.F. Pommaret, Differential Galois theory, New York-Paris-London 1983.
H. Umemura, On the irreducibility of the first differential equation of Painlevé, in Algebraic geometry and commutative algebra in honor of Masayoshi Nagata, Tokyo 1987, pp. 101-19.
H. Umemura, Differential Galois theory of infinite dimension, in Nagoya mathematical journal, 1996.

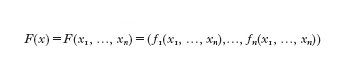
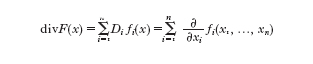
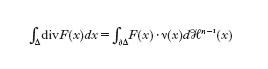
![[4]](https://images.treccani.it/ext-tool/intra/thumbs_medium/b/ba/FORMULE_equazioni_04.jpg)
![[5]](https://images.treccani.it/ext-tool/intra/thumbs_medium/6/6d/FORMULE_equazioni_05.jpg)
![[6]](https://images.treccani.it/ext-tool/intra/thumbs_medium/4/4a/FORMULE_equazioni_06.jpg)

![[8]](https://images.treccani.it/ext-tool/intra/thumbs_medium/b/b3/FORMULE_equazioni_08.jpg)
![[9]](https://images.treccani.it/ext-tool/intra/thumbs_medium/2/20/FORMULE_equazioni_09.jpg)
![[10]](https://images.treccani.it/ext-tool/intra/thumbs_medium/a/ac/FORMULE_equazioni_10.jpg)
![[1]](https://images.treccani.it/ext-tool/intra/thumbs_medium/5/5b/FORMULE_equazioni_11.jpg)
![[2]](https://images.treccani.it/ext-tool/intra/thumbs_medium/1/14/FORMULE_equazioni_12.jpg)
![[3]](https://images.treccani.it/ext-tool/intra/thumbs_medium/f/fb/FORMULE_equazioni_13.jpg)
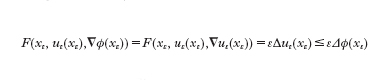
![[4]](https://images.treccani.it/ext-tool/intra/thumbs_medium/2/24/FORMULE_equazioni_15.jpg)
![[5]](https://images.treccani.it/ext-tool/intra/thumbs_medium/d/dc/FORMULE_equazioni_16.jpg)
![[6]](https://images.treccani.it/ext-tool/intra/thumbs_medium/b/b2/FORMULE_equazioni_17.jpg)
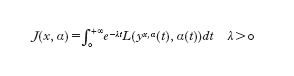
![[7]](https://images.treccani.it/ext-tool/intra/thumbs_medium/5/58/FORMULE_equazioni_19.jpg)
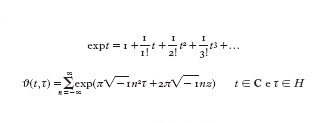
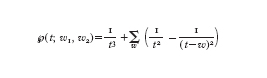
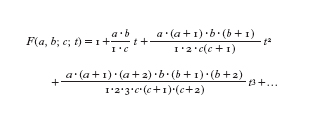
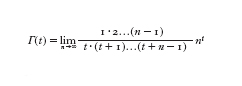
![[1]](https://images.treccani.it/ext-tool/intra/thumbs_medium/4/49/FORMULE_equazioni_24.jpg)