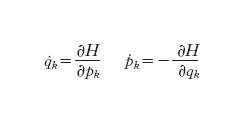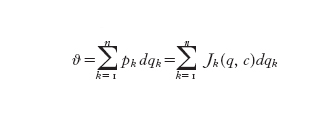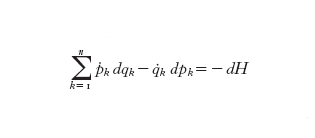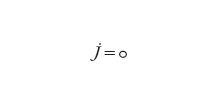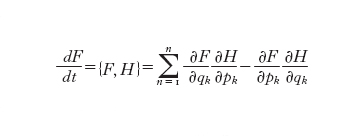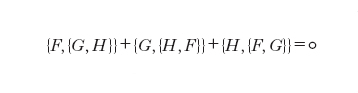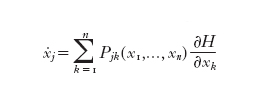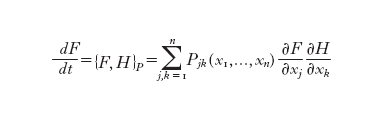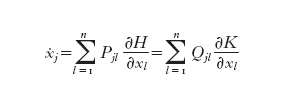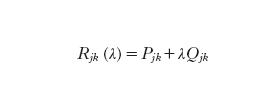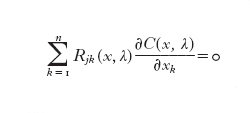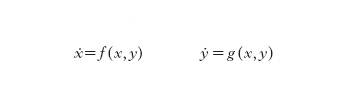SISTEMI DINAMICI

Sistemi dinamici

Il concetto di sistema è presente nel dibattito scientifico degli ultimi decenni nelle più diverse discipline: dall'idea di sistema fisico a quella di ecosistema, dai sistemi sociali ai sistemi progettati dalla moderna ingegneria. Tipica, dal punto di vista della teoria dei sistemi, è l'attenzione ai processi di informazione e di controllo, che segue la via aperta dalla cibernetica e in particolare le sollecitazioni provenienti dalle metodologie e dalle tecniche dell'automatica (v. sistemi, App. IV, iii, p. 347; V, iv, p. 802); inoltre è rilevante l'interesse per il trattamento della complessità (v. complessità: Sistemi complessi, in questa Appendice). Alla teoria dei sistemi è stato attribuito, fin dai primi contributi teorici (fra cui spicca quello pioneristico di L. von Bertalanffy), un ruolo unificatore nella scienza contemporanea: tale ruolo si presenta come alternativo all'approccio alla realtà proprio del meccanicismo (v. meccanicismo, XXII, p. 663). Se si attenua, almeno nelle intenzioni, l'influsso concettuale della meccanica classica, non per questo si indebolisce la posizione centrale della matematica nella spiegazione dei più svariati fenomeni naturali, sociali o artificiali; anzi, ai metodi e concetti matematici usati dalla fisica matematica classica - in primo luogo le equazioni differenziali ordinarie e alle derivate parziali - si affiancano altri strumenti, come quelli della teoria dei giochi, della statistica, della ricerca operativa, della teoria del controllo e dell'analisi numerica al calcolatore, settori della matematica applicata oggi in grande sviluppo (v. modellistica matematica, in questa Appendice). In questo contesto gli studi sui sistemi descritti da equazioni differenziali ordinarie sono oggetto di un rinnovato interesse da parte dei matematici, che si sono confrontati anche con i sistemi non lineari presenti in molti esempi applicativi (v. equazioni differenziali, App. V, ii, p. 131); sono state messe a punto delle nuove tecniche geometriche, seguendo un'impostazione già avanzata da H. Poincaré all'inizio del Novecento nel corso dei suoi studi di meccanica celeste: quest'impostazione aveva atteso per decenni adeguati sviluppi.

Nel seguito vengono presentati alcuni aspetti delle ricerche recenti in quest'ambito. Mentre proseguono gli studi sui sistemi hamiltoniani (uno dei capitoli centrali della meccanica, che ha portato alla moderna teoria dei sistemi integrabili), per questo settore di ricerca si è diffusa la denominazione generale di teoria dei sistemi dinamici. Questa è divisa a sua volta in diverse branche, a seconda delle tecniche e delle strutture matematiche trattate; la sua grande vivacità è testimoniata dalla nascita dal suo interno di nuove discipline, come la geometria simplettica, mentre nel contempo trovano risposta problemi classici che hanno atteso lungo tempo per essere risolti.

Sistemi integrabili

di Franco Magri

La teoria dei s. d. integrabili, nata al tempo di Newton con la risoluzione del problema del moto dei pianeti attorno al Sole, ha contrassegnato, con le sue crisi e i suoi successi, la storia della meccanica (v. fisica matematica: Il teorema KAM, in questa Appendice). Nel periodo classico, marcato dalla profonda influenza dell'opera di K.G. Jacobi, tale teoria si identifica praticamente con lo studio dei casi di integrabilità dell'equazione di Hamilton-Jacobi. Il risultato principale è ottenuto da J. Liouville, che indica una via diretta per risolvere l'equazione di Hamilton-Jacobi nel caso in cui si conosca un'opportuna famiglia di costanti del moto.

Quest'impostazione entrò in crisi alla fine dell'Ottocento, nel momento in cui H. Poincaré ed E.H. Bruns dimostrarono la non esistenza di integrali algebrici, distinti dagli integrali classici, per il problema dei tre corpi (Whittaker 1904). Le ricerche moderne hanno inizio con la nascita della teoria dei gruppi di trasformazione dovuta a S. Lie, la quale ha permesso di rendere precisa la nozione di simmetria di un sistema dinamico e ha aperto la porta all'importante osservazione, fatta da E. Noether nel 1917, secondo la quale esiste uno stretto legame tra costanti del moto e simmetrie di un sistema dinamico hamiltoniano. Progressivamente l'idea di simmetria permea in profondità la teoria dei s. d. integrabili, modificandone in molti tratti essenziali la forma. L'aspetto più saliente di questo processo è il carattere sempre più marcatamente geometrico della teoria, che contrasta in maniera singolare con la natura analitica dell'impostazione di Jacobi. Sotto l'influenza di E. Cartan la teoria dei s. d. integrabili diventa un capitolo della geometria simplettica (Abraham, Marsden 1978) con il contributo fondamentale di V.I. Arnol´d.

Dalla fine degli anni Sessanta le ricerche sui sistemi integrabili si sono sviluppate al di fuori dell'ambito tradizionale della meccanica classica. L'occasione è stata fornita dalla scoperta di un'ampia classe di equazioni non lineari alle derivate parziali della fisica matematica che possono essere considerate l'analogo infinito-dimensionale dei s. d. hamiltoniani integrabili. Alcuni esempi sono dati dall'equazione di Korteweg-de-Vries, dall'equazione di Schrödinger non lineare, dai cosiddetti sistemi di Moser-Calogero, dai reticoli di Toda e così via. Per tali equazioni è stato sviluppato un metodo specifico di integrazione detto metodo dello scattering inverso (Symplectic geometry, 1990). Sebbene tale metodo non faccia direttamente uso della teoria hamiltoniana, si è lentamente compreso che l'aspetto che accomunava le diverse equazioni era la proprietà di essere dei sistemi hamiltoniani in senso generalizzato. La nuova teoria veniva così ad avere un impatto profondo sulla teoria classica dei s. d. integrabili, costringendola a rimettere in discussione alcune delle sue premesse iniziali. Nel seguito verranno delineati i cambiamenti concettuali apportati dal metodo dello scattering inverso nella teoria dei sistemi integrabili, collocando gli sviluppi recenti sullo sfondo della teoria classica.

Le costanti del moto e la nozione di integrabilità

La teoria classica dei s. d. integrabili si fonda sullo stretto legame che intercorre tra il sistema di Hamilton

e l'equazione di Hamilton-Jacobi

È noto infatti, dalla teoria delle caratteristiche, che per costruire la soluzione generale delle equazioni di Hamilton è sufficiente procurarsi un integrale completo dell'equazione di Hamilton-Jacobi. Si tratta di un'impostazione introdotta nello studio del moto per ricondurre la meccanica al principio di conservazione dell'energia, ma che si applica in generale allo studio dei s. d. conservativi hamiltoniani (v. dinamica: Dinamica generale, XII; statistica, meccanica, XXXII). Allo scopo di ottenere un integrale completo dell'equazione di Hamilton-Jacobi si può seguire il seguente procedimento suggerito da Liouville nel 1855. Si supponga di conoscere n costanti del moto del sistema hamiltoniano, cioè n funzioni I_k (q, p) delle posizioni e dei momenti che siano costanti sulle traiettorie del sistema hamiltoniano (con n si indica, al solito, il numero dei gradi di libertà del sistema). Si supponga inoltre che tali funzioni siano indipendenti e in involuzione fra di loro (ciò significa che la parentesi di Poisson di una qualsiasi coppia di funzioni I_k e I_j è identicamente nulla: v. equazioni, XIV, pp. 137-38). Vengono attribuite a queste funzioni n valori costanti (c₁,...,c_n) e si risolvono le equazioni algebriche I_k (q,p)=c_k rispetto ai momenti canonici. Con le funzioni p_k=J_k (q,c) così ottenute si costruisce la forma differenziale di Liouville

Secondo Liouville questa forma differenziale è esatta, cioè esiste un potenziale W tale che ϑ=dW(q,c); il potenziale W(q,c) è l'integrale completo cercato dell'equazione di Hamilton-Jacobi. Questo teorema è stato talmente importante negli sviluppi successivi della teoria che si è presa l'abitudine di definire integrabile un s. d. hamiltoniano che ammette n costanti del moto in involuzione.

Simmetrie, gruppi di Lie e geometrizzazione

Il primo significativo cambiamento nel quadro concettuale della teoria dei s. d. integrabili fu prodotto dalla nascita della teoria dei gruppi di trasformazione (v. equazioni, XIV, p. 140) e dall'introduzione della nozione di simmetria di un sistema dinamico. Lo studio delle simmetrie richiede la presenza di un quadro geometrico preciso e globale dello spazio su cui il s. d. è definito: in tal modo lo studio delle proprietà geometriche delle equazioni di Hamilton prende progressivamente il posto dello studio dell'integrale completo di Hamilton-Jacobi. Il punto di partenza dell'analisi geometrica è l'osservazione che è possibile riscrivere le equazioni di Hamilton nella forma compatta

come si riconosce moltiplicando le equazioni di Hamilton per i differenziali delle coordinate e dei momenti e combinando i risultati in modo da far comparire il differenziale della hamiltoniana.

Questa semplice manipolazione formale trasforma le equazioni di Hamilton in una relazione tra forme differenziali e spalanca la porta all'ingresso della 'geometria simplettica' nella meccanica hamiltoniana. Lo schema astratto a cui si perviene può essere descritto con il seguente linguaggio: un s. d. è rappresentato da un campo vettoriale su una varietà. Tale varietà ha una propria struttura, detta simplettica, che permette di associare a ogni campo vettoriale una forma differenziale detta forma simplettica. Da questo punto di vista una varietà simplettica non differisce molto da una varietà riemanniana, dove lo stesso tipo di legame è realizzato dal 'tensore metrico' della varietà. La struttura simplettica permette di distinguere i campi vettoriali in due classi: i campi hamiltoniani, a cui corrispondono forme differenziali esatte, e i campi non hamiltoniani. Questo punto di vista introduce un'importante svolta concettuale nella teoria hamiltoniana, in quanto relativizza la nozione di campo vettoriale hamiltoniano. Esso mostra che, se non si precisa quale forma simplettica si considera, non ha senso chiedersi se un dato campo vettoriale sia hamiltoniano; potrebbe in effetti accadere che un campo vettoriale sia hamiltoniano rispetto a una struttura simplettica ma non rispetto a un'altra, oppure che lo sia rispetto a più strutture simplettiche simultaneamente. Senza sfruttare per ora questa libertà nella scelta della struttura simplettica, nel seguito si procede, come d'abitudine nella meccanica classica, ritenendo tale struttura fissata a priori. Alla fine di questa voce si riprende, tuttavia, questo importante tema cercando di mostrare come esso sia centrale nella moderna teoria dei s. d. integrabili.

Una conseguenza inevitabile dell'abbandono del punto di vista analitico e dell'equazione di Hamilton-Jacobi è la necessità di reinterpretare il teorema di Liouville. La costruzione dell'integrale completo prima descritta deve ora essere interamente riformulata in linguaggio geometrico. Si parte dall'analisi dei gruppi di simmetria del sistema dinamico. Come primo passo si dimostra che è sufficiente richiedere al gruppo, affinché sia un gruppo di simmetria, di lasciare invariate separatamente la struttura simplettica e la hamiltoniana del sistema. Si analizza poi il gruppo di simmetria tramite i sottogruppi a un parametro, ciascuno dei quali è completamente caratterizzato da un campo vettoriale detto il generatore del sottogruppo. Come conseguenza della proprietà di lasciare invariata la struttura simplettica, si dimostra che tale generatore è un campo vettoriale hamiltoniano (rispetto alla struttura simplettica fissata) e perciò a esso è associata una funzione hamiltoniana. Nel loro insieme queste funzioni hamiltoniane definiscono un'applicazione J:M→g* dallo spazio delle fasi al duale dell'algebra di Lie del gruppo di simmetria. Tale applicazione è detta applicazione momento associata al gruppo di simmetria. Come conseguenza della proprietà dei singoli sottogruppi di lasciare invariata la hamiltoniana del sistema, si dimostra che l'applicazione momento è una costante del moto e cioè (teorema di Noether):

formula [

1]

Per arrivare al teorema di Liouville bisogna fare l'ulteriore ipotesi che il gruppo di simmetria sia abeliano e che la sua dimensione sia pari al numero dei gradi di libertà del sistema dinamico. Si prendono allora in esame le superfici di livello dell'applicazione momento e se ne studia in dettaglio la topologia. Si mostra, nelle ipotesi che il valore di J non sia critico e che le superfici di livello siano compatte, che tali superfici hanno la topologia di tori n-dimensionali; infine si verifica che la restrizione su ogni toro invariante del s. d. sia un 'flusso alla Kronecker', cioè l'analogo per il toro di un moto rettilineo e uniforme nello spazio euclideo. In questo modo si giunge a dare una rappresentazione completa dei moti del sistema (Arnol´d 1974).

Dalle azioni non simplettiche ai gruppi quantistici

Il trattato di R. Abraham e J. Marsden, Foundations of mechanics (1978), fornisce una rappresentazione completa e significativa della teoria dei sistemi hamiltoniani con simmetria finora delineata, nota anche come teoria di Arnol´d-Liouville. All'interno di questo quadro si è sviluppata, a partire dagli anni Settanta, la moderna teoria dei sistemi integrabili, seguendo tre direzioni: lo studio delle singolarità dell'applicazione momento, l'integrabilità non commutativa e le azioni non simplettiche.

La prima linea di ricerca rappresenta un completamento della teoria di Arnol´d-Liouville. Con lo studio delle superfici di livello corrispondenti a valori critici dell'applicazione momento si porta a compimento il programma di determinare la topologia globale di un s. d. integrabile. Nella seconda linea di ricerca si fa cadere l'ipotesi che il gruppo di simmetria sia abeliano. In questo caso è come se i singoli gruppi a un parametro in cui si può analizzare il gruppo di simmetria non cooperassero più all'unisono. Non è più sufficiente che la dimensione del gruppo di simmetria sia pari al numero dei gradi di libertà del sistema. Occorre conoscere più simmetrie, tante più quanto più il gruppo è non abeliano. Come misura della non abelianità del gruppo si può prendere il rango della sua algebra di Lie, cioè la codimensione di una generica orbita coaggiunta. Nel teorema di integrabilità non commutativa si dimostra che, se la dimensione 2n della varietà simplettica eguaglia la somma della dimensione del gruppo e del suo rango, si ha una struttura simile a quella del teorema di Liouville. Anche in questo caso si possono individuare dei tori invarianti, di dimensione pari al rango dell'algebra di Lie, su cui il flusso del s. d. è un flusso di Kronecker (Symplectic geometry, 1990, p. 67).

La terza linea di sviluppo è più profonda; essa ha a che fare con la versione quantistica del metodo dello scattering inverso (metodo usato, per es., da L.D. Faddeev, E.K. Skljanin, N.Ju. Rešetichin e altri nello studio dell'equazione di Yang-Baxter in meccanica statistica negli anni Settanta e Ottanta). Per spiegare la relazione con i sistemi integrabili si parte dall'osservazione che non è necessario che l'azione di un gruppo sia simplettica affinché la parentesi di Poisson di due funzioni invarianti rispetto all'azione del gruppo sia ancora una funzione invariante. Quest'osservazione ha spinto V.G. Drinfel´d a introdurre una classe più ampia di azioni, che generalizza la classe delle azioni simplettiche. Tale estensione ha il suo prezzo. Per 'controllare' in maniera ragionevole il difetto di simpletticità dell'azione bisogna imporre al gruppo di Lie una struttura supplementare: la struttura di gruppo di Poisson. È impossibile, in poche righe, rendere più precisa questa nozione. Ci basti segnalare questa linea di sviluppo e rimarcare come essa rappresenti, per così dire, una 'rivincita' della teoria dei sistemi integrabili sulla teoria dei gruppi di Lie. Fino al lavoro di Drinfel´d era stata la teoria dei gruppi di Lie a 'imporsi' sulla teoria dei sistemi integrabili, cambiandone la natura e dandole una forma coerente con la propria struttura concettuale. Da allora tale rapporto sembra rovesciarsi: sono le esigenze concettuali della teoria dei sistemi integrabili che, per la prima volta, si fanno sentire nell'ambito della teoria dei gruppi, portando, in un certo senso, all'introduzione di una nuova nozione di gruppo (per il concetto di gruppo quantistico, v. Chari, Pressley 1994). Gli sviluppi di questa nuova linea di ricerca sono assai rapidi e dalla portata ancora imprevedibile; quello più interessante è stato suggerito dal tentativo di estendere la teoria dei gruppi di Poisson dai sistemi classici a quelli quantistici (sulla quantizzazione o passaggio da una teoria classica a una quantistica v. campi, teoria dei, App. IV e matematica non commutativa, in questa Appendice). Senza dubbio la teoria di questi nuovi gruppi è uno dei segni più convincenti della persistente vitalità della teoria dei sistemi integrabili, ma non la esaurisce. Nuove linee di ricerca, ancora più sorprendenti, ne sono derivate.

Rappresentazione di Lax e geometria algebrica

Un modo nuovo di affrontare lo studio dell'integrabilità di un s. d. è stato suggerito da P. Lax nel 1968. Motivato dallo studio dei sistemi a un numero infinito di gradi di libertà descritti da equazioni alle derivate parziali, Lax propose di considerare quei s. d. che potevano essere scritti nella forma

formula [

2]

oggi comunemente detta rappresentazione di Lax. Questo tipo di rappresentazione si è rivelata utile in un numero sorprendentemente grande di esempi. Non solo si è scoperto che molti s. d. classici, di cui era nota l'integrabilità, ammettevano rappresentazione alla Lax, ma si è anche stati in grado di costruire nuovi esempi di sistemi integrabili rovesciando il processo.

Ciò significa che si può costruire un s. d. a partire da una scelta oculata delle matrici L e P come funzioni delle 'coordinate' e dei 'momenti': è sufficiente che tali coordinate evolvano nel tempo in modo che l'equazione [2] abbia senso. L'articolo di B.A. Dubrovin, I.M. Krichever e S.P. Novikov (in Symplectic geometry, 1990) contiene un'esposizione dei molti casi trattati con questa tecnica; bisogna sottolineare le analogie tra la mappa di Lax e l'applicazione momento discussa in precedenza. Come J, anche L può essere pensata come una mappa dallo spazio delle fasi nel duale di un'algebra di Lie. La differenza è nella legge di evoluzione temporale. Mentre a J si impone di essere costante nel tempo (equazione [1]), a L si concede di variare secondo la legge preassegnata (equazione [2]). Questa generalizzazione ha dato origine a una nuova tecnica di integrazione chiamata integrabilità algebrico-geometrica in cui confluiscono e si integrano in maniera proficua molte idee di geometria simplettica e di geometria algebrica. Le radici di questa tecnica risalgono molto indietro nel tempo, ai lavori di Jacobi sulla separabilità dell'equazione di Hamilton-Jacobi, ma le sue forme sono completamente nuove. Spesso ci si riferisce a essa come alla costruzione di Jacobi-Mumford. Ci limiteremo qui a dare un breve cenno dello spirito del metodo (Symplectic geometry, 1990).

Condizione preliminare per il successo dell'integrabilità algebrico-geometrica è che le equazioni del moto ammettano una rappresentazione alla Lax con matrici L e P che dipendono da un parametro complesso λ, detto parametro spettrale. In molti esempi L(λ) dipende polinomialmente da λ e in maniera complicata dalle coordinate sullo spazio delle fasi. Per ipotesi, durante il moto del sistema, la matrice L(λ) verifica l'equazione [2]. Essa non è perciò costante ma la sua legge di evoluzione temporale è certamente di tipo particolare. Per metterne in evidenza il significato si concentri l'attenzione sugli autovalori della matrice L(λ), uguagliando a zero il polinomio caratteristico det(L(λ)−μI)=0. Quest'equazione definisce una curva algebrica nel piano complesso, detta curva spettrale. I coefficienti di questa curva dipendono, tramite la matrice di Lax, dalle coordinate del punto nello spazio delle fasi. Ci si potrebbe quindi attendere che durante il moto del sistema la curva si sposti nel piano complesso: così non è. L'equazione [2] impone alla curva spettrale di rimanere fissa nel piano complesso e agli autovalori della matrice di Lax di essere delle costanti del moto. L'equazione [2] rappresenta perciò la condizione di isospettralità della matrice di Lax.

Altre preziose informazioni sulle equazioni del moto possono essere dedotte dallo studio dell'evoluzione temporale degli autovettori della matrice di Lax. Qui la teoria si fa complicata e ancora parzialmente incompleta. Il metodo si basa sullo studio delle singolarità degli autovettori definiti nei punti della curva spettrale. Tramite considerazioni di geometria algebrica, si estraggono dalla matrice di Lax due polinomi particolari che descrivono le singolarità degli autovettori. La scelta di questi polinomi è ancora un'arte piuttosto che un algoritmo. Di uno di questi polinomi si considerano gli zeri; dell'altro si considerano i valori assunti in corrispondenza degli zeri precedenti. Gli zeri del primo polinomio e i valori del polinomio coniugato definiscono un sistema di coordinate privilegiate sullo spazio delle fasi. Si dimostra che in tali coordinate l'integrazione delle equazioni differenziali del moto si riduce al calcolo di opportuni integrali abeliani sulla curva spettrale della matrice di Lax. La procedura indicata rappresenta una nuova tecnica di integrazione delle equazioni che ammettono rappresentazione alla Lax con parametro spettrale. I s. d. descritti da tali equazioni sono detti sistemi algebricamente completamente integrabili.

Sistemi bihamiltoniani e coppie di Poisson

L'ultimo sviluppo della moderna teoria dei s. d. integrabili che viene illustrato ha la sua origine nell'evoluzione del concetto di s. d. hamiltoniano. Già alla fine del 19° sec. Lie aveva proposto una generalizzazione della nozione di sistema hamiltoniano basata sull'uso delle parentesi di Poisson. Ricordiamo che la derivata temporale di una funzione scalare F lungo le traiettorie di un usuale campo hamiltoniano è data dalla parentesi di Poisson

delle funzioni F e H, che, è noto, verifica l'identità ciclica di Jacobi

Lie propose di estendere la nozione di campo hamiltoniano sostituendo le usuali equazioni di Hamilton con un sistema differenziale

dove la matrice dei coefficienti sia antisimmetrica ma non necessariamente costante né invertibile. Diremo che tale s. d. è hamiltoniano se la nuova parentesi di Poisson, definita dalla relazione

verifica ancora l'identità ciclica di Jacobi. In questo caso alla matrice dei coefficienti P_jk (x₁,...,x_n) si dà il nome di bivettore di Poisson.

Questa è la definizione più generale, oggi conosciuta, di s. d. hamiltoniano. Essa evidenzia che un campo vettoriale è hamiltoniano solo se può essere fattorizzato nel prodotto di un bivettore di Poisson e di una forma differenziale esatta. Nulla vieta che questa fattorizzazione non sia unica, cioè che esistano campi vettoriali che si decompongono in forme hamiltoniane rispetto a due diversi bivettori di Poisson. Tali campi sono detti bihamiltoniani. Sperimentalmente si verifica che molti sistemi che ammettono rappresentazione alla Lax sono bihamiltoniani. Questa constatazione rafforza l'idea che esista uno stretto legame tra i sistemi integrabili e quelli bihamiltoniani. Lo sviluppo di quest'idea deve molto all'opera di I.M. Gel´fand (Gelfand, Zakharevich 1993).

Consideriamo un campo bihamiltoniano

formula [

3]

Si dice che i bivettori P_jl e Q_jl formano una coppia di Poisson se il fascio lineare dei bivettori

formula [

4]

verifica l'identità di Jacobi per ogni valore del parametro λ (che svolge lo stesso ruolo del parametro spettrale nella teoria di Lax). Gel´fand ha scoperto un modo per integrare le equazioni del moto [3] utilizzando la coppia di Poisson. Per far questo bisogna costruire la funzione di Casimir C(λ) del fascio di Poisson [4]. Tale funzione verifica l'equazione

in ogni punto x dello spazio delle fasi oltre che per ogni valore del parametro spettrale λ. Se la dimensione dello spazio delle fasi è dispari, diciamo dim H=2n+1, si può scegliere C(x,λ) nella forma di un polinomio di grado n in λ:

In questo modo il fascio di Poisson fornisce una famiglia di n +1 funzioni (C₀(x),...,C_n(x)). Fissiamo una superficie di livello S della funzione C₀(x). Gel´fand ha mostrato che S è una varietà simplettica a cui il campo hamiltoniano è tangente e che le funzioni (C₁(x),..., C_n(x)), ristrette a S, costituiscono una famiglia di funzioni in involuzione rispetto alla struttura simplettica di S. Ritorniamo così alla situazione delineata all'inizio nel caso della teoria di Arnol´d-Liouville. Se le funzioni (C₀(x),..., C_n(x)) sono delle costanti del moto del campo bihamiltoniano dato dall'uguaglianza [3], come capita usualmente, i moti sono dei flussi di Kronecker su dei tori invarianti. L'idea suggestiva alla base della teoria di Gel´fand è che questa procedura possa essere in qualche modo rovesciata, nel senso che si possa risalire a un fascio di Poisson ogni volta che si ha una famiglia massimale di funzioni in involuzione. Se così fosse, si aprirebbero nella teoria dei sistemi integrabili degli scenari completamente inesplorati sicuramente materia di studi futuri.

bibliografia

E.T. Whittaker, A treatise on the analytical dynamics of particles and rigid bodies, Cambridge 1904, 1988⁴.

V.I. Arnold, Matematičeskie metody klassičeskoj mechaniki, Moskva 1974 (trad. it. Metodi matematici della meccanica classica, Roma 1979).

R. Abraham, J. Marsden, Foundations of mechanics, Reading (Mass.) 1978.

Symplectic geometry and its applications, in Encyclopaedia of mathematical sciences, ed. V.I. Arnold, S.P. Novikov, 4° vol., Berlin-New York 1990.

I.M. Gelfand, I.Zakharevich, On the local geometry of a bihamiltonian structure, in The Gelfand mathematical seminars 1990-1992, Boston 1993.

V. Chari, A. Pressley, A guide to quantum groups, Cambridge-New York 1994.

Sistemi dinamici e geometria simplettica

di Dmitrij Anosov

La teoria dei s. d. - ivi comprese questioni affini della teoria delle equazioni differenziali ordinarie e di altre discipline matematiche - si può suddividere in quattro settori principali che sono caratterizzati dalla presenza e dall'utilizzo di una certa struttura nello spazio delle fasi: la dinamica differenziale (teoria dei s. d. lisci o smooth), la dinamica topologica (teoria dei s. d. topologici), la teoria ergodica (in cui lo spazio delle fasi è ipotizzato misurabile, spesso, con misura assegnata) e la teoria analitica (in cui lo spazio delle fasi e il tempo - variabile indipendente - si ipotizzano complessi). Evidentemente un s. d., in generale, presenta contemporaneamente più di una fra le suddette strutture, per es., i s. d. hamiltoniani (v. sopra) hanno delle peculiarità legate alla struttura simplettica, e tuttavia il loro studio è stato sempre considerato come parte integrante della teoria dei s. d. lisci. Tradizionalmente questa suddivisione è stata comunque ritenuta significativa e sostanzialmente rispettata. A questi settori ormai classici si è aggiunta una nuova disciplina, la geometria simplettica (o topologia simplettica), sviluppatasi soprattutto a partire dagli anni Ottanta, che ha per lo meno lo stesso livello dei suddetti quattro settori tradizionali della teoria dei s. d., e, in parte, va anche oltre quest'ultima. Poiché non è frequente la formazione di nuove discipline di tale importanza, quest'evento merita una particolare attenzione anche se, certamente, eventi di minor importanza 'tassonomica' possono essere altrettanto significativi per il loro contenuto: basti ricordare la creazione della teoria KAM (v. fisica matematica: Il teorema KAM, in questa Appendice) e la 'rivoluzione iperbolica' degli ultimi vent'anni (v. oltre). In precedenza gli argomenti e i risultati 'simplettici' venivano considerati come parte della dinamica differenziale o della geometria differenziale. È merito di V. I. Arnol´d aver sottolineato insistentemente, a partire dalla metà degli anni Sessanta, che si era in presenza di un complesso di nozioni e metodi relativamente autonomo e coerente. Egli si è occupato di questi temi in profondità, esaminandoli - cosa di particolare rilievo - in svariati contesti: sistemi hamiltoniani, metodi asintotici per le equazioni differenziali alle derivate parziali e così via.

È chiaro a posteriori come la teoria delle singolarità lagrangiane (dovuta ad Arnol´d e alla sua scuola) e la teoria delle intersezioni delle varietà lagrangiane (dovuta ad A. Weinstein), nate nel ventennio precedente, fossero una sorta di 'messaggeri' della nuova disciplina, nella quale successivamente sono entrate in modo organico. Le suddette nozioni, così come anche una serie di nozioni affini, erano presenti in modo implicito nell'apparato matematico della meccanica analitica classica; la loro individuazione ed evidenziazione è dovuta a V.P. Maslov e ad Arnol´d. Uno stimolo importante per la sviluppo della geometria simplettica è venuto dalle ricerche di Ch. Conley ed E. Zehnder, volte a provare, per il toro n-dimensionale, la congettura di Arnol´d sui punti fissi dei diffeomorfismi simplettici 'esatti'. Nella dimostrazione si combinavano due idee introdotte precedentemente e che erano già state applicate in altri tipi di problemi: il nuovo approccio variazionale alle soluzioni periodiche dei s. d. hamiltoniani (dovuto a P. Rabinowitz) e l'idea di Conley sulla caratterizzazione topologica del comportamento delle traiettorie in prossimità di alcuni insiemi invarianti (gli insiemi 'localmente massimi' o 'isolati') mediante una certa generalizzazione dell'indice classico di Morse relativo alle posizioni di equilibrio del flusso gradiente (M. Morse, in effetti, parlava dei punti critici della funzione, il che è equivalente). La congettura di Arnol´d è stata provata nel seguito anche in altri casi, e vari autori hanno annunciato recentemente di aver ottenuto dimostrazioni nel caso generale. Vi sono anche altre applicazioni della geometria simplettica ai s. d., innanzitutto ai problemi relativi alle soluzioni periodiche (Hofer, Zehnder 1994).

Un contributo fondamentale, che segna l'esordio della topologia simplettica come disciplina autonoma, è il lavoro di M. Gromov (1985) sulle curve pseudo-olomorfe in varietà quasi-complesse. È noto che su una varietà kahleriana le strutture complesse e riemanniane sono date e inoltre, associata a queste (e ben collegata), si ha la struttura simplettica. Viceversa si verifica che, se viene data una struttura simplettica su una varietà differenziale, allora esistono più strutture quasi-complesse e riemanniane le quali, in un certo senso, sono compatibili con la struttura simplettica come nel caso più familiare delle varietà kahleriane (o algebriche). Si deve tener presente che in questo caso però non esiste una struttura complessa e riemanniana 'preferenziale': esiste invece un'intera classe di strutture le quali sono compatibili con la struttura simplettica iniziale. Ciononostante, per alcuni importanti risultati di geometria complessa esistono degli analoghi nella teoria simplettica. Lo studio di questi problemi, nonché l'impostazione generale, si allontana dalla teoria dei s. d., poiché Gromov utilizza alcuni sistemi di equazioni alle derivate parziali e i suoi risultati si applicano anche a problemi estranei alla teoria dei sistemi dinamici. I migliori risultati sulle soluzioni periodiche dei s. d. di Hamilton (dovuti a C. Viterbo, H. Hofer ed E. Zehnder) sono stati ottenuti seguendo questa via. Segnaliamo infine altri due gruppi di lavori collegati. Arnol´d ha iniziato lo studio di un gruppo di problemi, noti come teoria non lineare di Sturm. J. Franks, V. Bangert e N. Hingstön hanno provato che su una sfera bidimensionale con un'arbitraria metrica riemanniana esiste un numero infinito di geodetiche chiuse (un risultato precedente, che risale principalmente ai lavori di L.A. Ljusternik e L.G. Šnirel´man della fine degli anni Venti, ma portato successivamente fino alle ultime conseguenze, è quello di tre geodetiche chiuse caratterizzate dall'assenza di autointersezioni). Franks ha dimostrato un risultato analogo per le metriche con curvatura positiva, e in seguito Bangert si è occupato del caso generale. La dimostrazione dipendeva all'inizio da alcuni risultati inediti di M. Handel, ma Hingstön ha dimostrato come liberarsi da questa dipendenza. Un secondo indirizzo di ricerca che si è sviluppato negli ultimi anni, in questo caso senza uscire dall'ambito della dinamica differenziabile, è la dinamica conforme, vale a dire lo studio delle iterazioni delle funzioni analitiche nel dominio complesso (per una suggestiva introduzione geometrica a questi studi, v. Peitgen, Richter 1986).

Soluzioni moderne ad alcuni problemi classici

di Dmitrij Anosov

Stabilità strutturale e 'rivoluzione iperbolica'

Il primo problema consiste nella caratterizzazione qualitativa del comportamento delle traiettorie dei sistemi strutturalmente stabili. Questo problema risale al lavoro di A.A. Andronov e L.S. Pontrjagin, che hanno introdotto la nozione stessa di sistema strutturalmente stabile e caratterizzato i flussi strutturalmente stabili sul piano (precisamente sulla sfera a due dimensioni). Nel corso della 'rivoluzione iperbolica', S. Smale formulò la seguente congettura: per la stabilità strutturale è condizione necessaria e sufficiente che l'insieme dei punti non vaganti sia iperbolico e che le rispettive varietà stabili e instabili abbiano solo intersezioni trasversali. La sufficienza è stata dimostrata in completa generalità da R.C. Robinson, mentre la necessità è stata provata solo più tardi, benché un passo molto importante fosse stato già fatto da Ch. Pugh che aveva dimostrato un lemma, a prima vista semplice, in realtà molto difficile, sulla chiusura. Esso afferma che, se il dato sistema liscio ha un punto non vagante x, con una perturbazione di classe C¹ arbitrariamente piccola, si può garantire che x sia periodico. Un lemma analogo non vale nella classe dei s. d. hamiltoniani. In quest'ultimo caso M. Herman e J. Xia hanno dimostrato che l'analogo C² del suddetto lemma non è valido. La necessità è stata provata per s. d. a tempo discreto da R. Mañé, e per i flussi da Sh. Hayashi (1997). È opportuno notare che è stato necessario aggiungere al lemma di chiusura altre asserzioni simili (ugualmente 'evidenti').

Il ventunesimo problema di Hilbert

In questo problema si chiede di dimostrare che esiste sempre un'equazione differenziale lineare (in realtà s'intende non un'equazione, ma un sistema) di tipo fuchsiano con punti singolari e gruppo di monodromia dati (correntemente si parla più precisamente di rappresentazione della monodromia).

Quando D. Hilbert propose il quesito nel 1900 forse si riferiva esclusivamente ai sistemi modernamente chiamati fuchsiani (tutte le singolarità di tali sistemi sono poli di primo ordine), ma potrebbe in realtà aver considerato quelli che nella terminologia odierna, più precisa, vengono detti sistemi regolari, che sono più 'abbondanti', ma le cui proprietà sono per molti versi analoghe alle proprietà di sistemi fuchsiani. Indipendentemente dalle possibili ambiguità della terminologia degli inizi del Novecento, esistono, effettivamente, due problemi: quello 'fuchsiano' e quello 'regolare'. Quest'ultimo fu risolto da J. Plemelj; fra l'altro si trattava della prima applicazione riuscita della teoria delle equazioni integrali singolari, le cui basi erano state poste da Plemelj proprio a questo proposito. Egli tentò di dedurre dal suo risultato positivo per il caso regolare anche quello per il caso fuchsiano. Solo verso il 1980 si è capito che in realtà la sua riduzione dipendeva da una condizione supplementare sulla rappresentazione della monodromia, vale a dire che egli aveva ottenuto soltanto una certa condizione sufficiente per la risolubilità positiva del ventunesimo problema nell'ambito fuchsiano. Rimaneva comunque la speranza che anche per sistemi fuchsiani la risposta fosse sempre positiva: la scoperta di un controesempio da parte di A.A. Bolibruch è stata una grande sorpresa. Continuando a lavorare in questa direzione, Bolibruch ha costruito, da una parte, una serie di controesempi di vario genere, dall'altra ha trovato alcune nuove condizioni sufficienti che garantiscono la risposta positiva (Anosov, Bolibruch 1994). I metodi da lui sviluppati hanno trovato applicazione anche in alcuni problemi della teoria analitica dei s. d. (per es. il problema di Birkhoff sulla forma normale di un sistema in prossimità di un punto singolare). È importante sottolineare che nei suoi lavori al posto delle equazioni integrali vengono spesso usate decomposizioni vettoriali, seguendo un approccio geometrico che è apparso per la prima volta negli anni Settanta in un lavoro di H. Rohrl dove si usa anche un raffinamento della teoria locale classica suggerita da A. Levelt in quegli stessi anni.

La congettura di Dulac

Sempre verso il 1980 è stato riesaminato un altro risultato classico: si tratta della congettura di Dulac, secondo la quale un sistema di due equazioni in R²

in cui f e g sono polinomi (di grado n), può avere solo un numero finito di cicli limite. H. Dulac stesso considerava la suddetta asserzione non una congettura ma un teorema, di cui fornì una dimostrazione nel 1923 seguendo un ragionamento poi rivelatosi incompleto. In realtà Dulac aveva capito bene che la dimostrazione si riduce all'analisi della trasformazione di una successione lungo il ciclo separatore e che la difficoltà del problema è legata alla non analiticità di questa trasformazione, della quale egli stabilì alcune proprietà che però non sono sufficienti per la deduzione richiesta. In seguito la congettura è stata dimostrata da R. Bamon per n=2; infine J. Écalle e Ju.S. Il´jašenko sono riusciti a provarla nel caso generale (Il´jašenko 1991; Écalle 1992). I metodi di questi due autori sono diversi, ed entrambi sono stati utilizzati anche in altri problemi: la teoria di Il´jašenko si dice geometrica, mentre l'approccio di Écalle è associato a un nuovo metodo di somma di serie divergenti, che si è rivelato utile per le equazioni differenziali ordinarie nella teoria analitica.

La congettura di Raghunathan

Un considerevole successo nella teoria dei s. d. di origine algebrica, ovvero dei cosiddetti flussi omogenei, è stata la dimostrazione, ottenuta da M. Ratner, sia della congettura di Raghunathan sia del suo analogo in teoria della misura, proposto da Sh. Dani (Ratner 1995; difatti in senso stretto non è corretto parlare di 'congettura di Raghunathan' in teoria della misura). Sia G un gruppo di Lie, queste congetture si riferiscono a un flusso unipotente (con 'tempo' multidimensionale) sullo spazio quoziente di volume finito G/D; il flusso è definito dall'azione di un sottogruppo unipotente U⊂G sulle classi laterali tramite la traslazione sinistra.

La prima congettura afferma che la chiusura di ogni traiettoria di tale flusso è un sottospazio omogeneo di volume finito; la seconda che qualsiasi misura ergodica per questo flusso (la quale sia finita sui compatti) è concentrata su qualche sottospazio di quel tipo e ammette una semplice descrizione algebrica, che deriva dalla misura di Haar sul sottogruppo, al quale è associato il sottospazio omogeneo. Nella dimostrazione svolge un ruolo importante una certa proprietà dei sottogruppi unipotenti a un parametro, chiamata proprietà di Ratner e da lui rilevata nel corso dei suoi precedenti lavori sui flussi omogenei, dedicati a questioni affatto diverse. Prima di questo notevole risultato erano stati provati vari casi particolari di entrambe le congetture. La maggior parte di essi concerne il flusso orociclico. G.A. Hedlund ottenne il primo risultato di questo genere già nel 1936. Secondo i criteri moderni, però, per il flusso orociclico la situazione è troppo semplice; in effetti, questi lavori non erano rivolti direttamente a dimostrare le congetture di Raghunathan e Dani, bensì a studiare in profondità le proprietà topologiche e metriche dei flussi considerati. G.A. Margulis ha dimostrato le suddette congetture nel caso molto più difficile di flussi unipotenti non orisferici nel quoziente SL(3,R)/SL(3,Z). Lo studio di tali flussi, effettuato da Margulis e Dani, ha condotto alla dimostrazione di una congettura della teoria dei numeri, e cioè la congettura di Oppenheim-Davenport sulle forme quadratiche. L'impressione diffusa è che nei lavori di Margulis e altri emerga un nuovo ramo della teoria geometrica dei numeri, in cui lo 'scenario' non sia più dato dallo spazio euclideo e dal toro, ma dai gruppi Lie e dai loro spazi omogenei. I più vicini al caso dello spazio euclideo sono i gruppi nilpotenti, i quali avevano cominciato a svolgere un ruolo particolare ancor prima di Margulis; bisogna però sottolineare che in precedenza, più che ottenere nuovi risultati in teoria dei numeri tramite queste tecniche, si era data un'interpretazione 'gruppale e dinamica' di fatti già noti.

La congettura di Seifert

Secondo la congettura di Seifert ogni flusso liscio sulla sfera tridimensionale S³ privo di punti di equilibrio (cioè punti dove la velocità di fase sia nulla) possiede necessariamente una traiettoria chiusa. La formulazione di questa congettura prende spunto da un teorema di G. Seifert, secondo il quale una traiettoria chiusa esiste per tutti i flussi ottenuti con una piccola perturbazione del flusso di Hopf, che sarà descritto nel seguito. Si consideri la sfera tridimensionale S³ come l'insieme di punti (z,w) del piano complesso bidimensionale C² per i quali |z|²1|w|²=1 (C² è quadrimensionale come spazio vettoriale su R). La velocità di fase del flusso di Hopf è un campo vettoriale che fa corrispondere al punto (z,w) il vettore (iz,iw). Le traiettorie del flusso di Hopf sono circonferenze della forma He^itz,e^itwJ; la scomposizione di S³ in queste circonferenze è nota in topologia come fibrato di Hopf. Oltre alla dimostrazione data da Seifert stesso, ci sono almeno altre due dimostrazioni del suo teorema, appartenenti a M. Bottkol e a F.B. Fuller. Quest'ultimo ha introdotto un indice (noto come indice di Fuller) che caratterizza il comportamento topologico delle traiettorie in prossimità della traiettoria chiusa; Bottkol ha usato una variante particolare della teoria delle perturbazioni (proposta da J. Moser in un lavoro sulle soluzioni periodiche in prossimità dei punti di equilibrio). I metodi di questi lavori hanno un significato più ampio, non individuabile nella dimostrazione di Seifert, ma anche questi riguardano solo le piccole perturbazioni del flusso di Hopf. Alla congettura di Seifert è associata la congettura del toro solido, il cui enunciato è il seguente: se in ogni punto della frontiera del 'toro solido' D²3S¹ il campo vettoriale della velocità di fase è indirizzato verso l'interno del toro solido (oppure ovunque verso l'esterno) e non ci sono punti di equilibrio nel toro, allora esiste una traiettoria chiusa. Intuitivamente sembra che quest'ultima debba fare, per così dire, un giro intorno al toro solido.

Grazie all'intensa attività di ricerca di molti autori, entrambe le congetture sono state smentite, anche per flussi analitici. F.W. Wilson ha costruito dei controesempi per gli analoghi multidimensionali della congettura di Seifert. Si tratta di un risultato che non può sorprendere (è abbastanza chiaro che nel caso multidimensionale le traiettorie quasiperiodiche possano del tutto 'sostituire' quella periodica, proprio ciò che accade nel lavoro di Wilson); è comunque un risultato importante in quanto una parte dei suoi accorgimenti tecnici è servita ad autori successivi. Sorprendente invece il controesempio di P. Schweizer (questo sì 'genuinamente' tridimensionale) proposto nel 1974, dato da un flusso differenziabile di classe C¹. Benché dopo tale esempio si fosse persa la fiducia per quel che riguardava le varianti più lisce di entrambe le congetture, non si è riusciti immediatamente ad alzare la proprietà di differenziabilità nei controesempi, e si è dovuto aspettare il contributo di J. Harrison. Infine K. Kuperberg (1994) ha proposto un controesempio differenziabile di classe C^`; E. Ghys e W. Thurston hanno indicato come ottenere un controesempio analitico tramite una modifica dell'esempio di Kuperberg.

bibliografia

M. Gromov, Pseudo-holomorphic curves on almost complex manifolds, in Inventiones mathematicae, 1985, 82, pp. 307-47.

H.-O. Peitgen, P.H. Richter, The beauty of fractals, images of complex dynamical systems, Berlin-New York 1986.

Yu.S. Il´jaèenko, Finiteness theorems for limit cycles (trad. dal russo), Providence (R.I.) 1991.

J. Écalle, Introduction aux fonctions analysables et preuve constructive de la conjecture de Dulac, Paris 1992.

D.V. Anosov, A.A. Bolibruch, The Riemann-Hilbert problem, Wiesbaden 1994.

H. Hofer, E. Zehnder, Symplectic invariants and Hamiltonian dynamics, Basel 1994.

K. Kuperberg, A smooth counterexample to the Seifert conjecture, in Annals of mathematics, 1994, 140, pp. 723-32.

D. McDuff, D. Salamon, Introduction to symplectic topology, Oxford-New York 1995.

M. Ratner, Interactions between ergodic theory, Lie groups and number theory, in Proceedings of the International congress of mathematicians, Zürich August 3-11, 1994, Basel-Boston 1995, pp. 157-82.

J.-Chr. Yoccoz, Recent developments in dynamics, in Proceedings of the International congress of mathematicians, Basel-Boston 1995, pp. 246-65.

Sh. Hayashi, Connecting invariant manifolds and the solutions of the C¹ stability and ø stability conjectures for flows, in Annals of mathematics, 1997, 145, pp. 81-137.

R. Berndt, Einführung in die symplektische Geometrie, Braunschweig 1998.

D. McDuff, Recent developments in symplectic topology, in 2^nd European congress of mathematics, Budapest July 22-26, 1996, ed. A. Balog et al., Boston 1998, 2° vol., pp. 28-42.