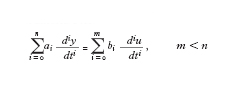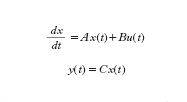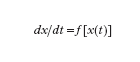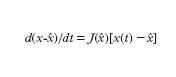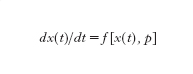COMPLESSITA'

Complessità

Il termine complessità è oggi frequentemente usato, in campo scientifico, in contesti diversi. In quello dell'informatica, dell'analisi numerica e dell'ottimizzazione, corrisponde alla caratteristica quantitativa di un algoritmo di calcolo, che determina la convenienza o la stessa possibilità di giovarsene per la soluzione pratica (automatica o anche manuale) di un problema, al quale viene attribuita la c. dell'algoritmo che lo risolve (v. informatica, App. V, ii, p. 704; e informatica: Scienze dell'informazione, in questa Appendice). Nel contesto dell'organizzazione e delle applicazioni tecnico-economiche corrisponde ad alcune caratteristiche strutturali del sistema. Nel contesto dei sistemi dinamici, la c. è generalmente considerata una caratteristica qualitativa di un sistema, concepito come un aggregato organico e strutturato di parti fra loro interagenti, la quale fa assumere al sistema stesso proprietà di comportamento non immediatamente riconducibili a quelle delle singole parti. Qui ci si occuperà soltanto di questo significato legato all'emergenza di nuovi aspetti del comportamento del sistema, non rilevabili al livello delle singole parti componenti, ma legati al modo in cui esse interagiscono. Con riferimento a questo significato del termine viene quindi spontaneo considerare stadi diversi e successivi di c. a partire da situazioni ancora abbastanza elementari.

I sistemi complessi presentano vari motivi d'interesse: per le implicazioni di natura pratica, come nel caso degli schemi di controllo a retroazione che si impiegano nel campo della tecnica (v. sistemi, App. IV, iii, p. 347 e V, iv, p. 802; controlli automatici, App. III, i, p. 430; IV, i, p. 523; V, i, p. 721); per gli aspetti concettuali degli strumenti matematici coinvolti, alcuni dei quali, come la teoria delle catastrofi o la geometria frattale, hanno ricevuto una notevole attenzione anche da parte dei mezzi di comunicazione di massa (v. caos e complessità, App. V, i, p. 490; catastrofi, teorema delle, App. V, i, p. 522; frattali, App. V, ii, p. 329; sistemi dinamici, in questa Appendice); per i concreti successi, oltre che per le speranze (talora eccessive), di utilizzare questi sistemi come modelli matematici utili per comprendere e governare fenomeni non facilmente rappresentabili con gli strumenti tradizionali, non solo nel campo delle scienze fisiche e delle loro applicazioni tecnologiche, ma anche in quelli delle scienze della vita, dell'uomo e della società (v. modellistica matematica, in questa Appendice); e inoltre per gli aspetti, di natura per certi versi filosofica, quali la capacità di molti sistemi a retroazione di dar conto di comportamenti (almeno apparentemente) orientati al conseguimento di un fine mediante il collegamento di parti ciascuna delle quali si comporta in modo rigidamente meccanicistico (e cioè, per usare la terminologia tradizionale, è influenzata solo da cause efficienti e non da cause finali), oppure la caratteristica del caos deterministico di associare (nel suo stesso nome, che a molti suona come un ossimoro) leggi rigorosamente deterministiche a comportamenti imprevedibili.

Tutto ciò spiega l'attenzione che i sistemi complessi hanno raccolto anche al di fuori degli ambiti specialistici, e spiega altresì le perplessità che eccessi ingenui di tale attenzione sollevano e che hanno determinato posizioni anche molto critiche nei riguardi della cosiddetta 'complessologia'. Per valutare queste diverse posizioni è opportuno tenere separati i diversi aspetti della questione. Nel seguito vengono esaminati gli aspetti matematici dei metodi di studio dei sistemi complessi, benché sia necessario usare prudenza riguardo alle speranze (spesso ingiustificate) di pervenire a formulazioni di tali metodi che risultino accessibili a un vasto pubblico di preparazione non specialistica. Per quanto riguarda invece le prospettive dell'impiego di tali metodi per la formulazione di modelli predittivi di fenomeni difficilmente rappresentabili con altri metodi matematici tradizionali, o quanto meno la possibile utilità della formulazione di modelli di tipo solo interpretativo (e cioè atti a dar conto in modo qualitativo di come il sistema si comporta e del perché si comporta in quel modo, ma non a prevederne quantitativamente il comportamento), si descrive il significato della c. in biologia. Infine vengono illustrati alcuni aspetti del problema della c. emersi nel dibattito filosofico recente a partire dalle idee sviluppate in ambito scientifico e tecnologico. L'impiego dei metodi in questione per lo studio di problemi diversi da quelli per i quali hanno già dato buon esito, anche se previsto e auspicato, è spesso ben lontano dall'attuazione e messo in discussione da taluni studiosi; difatti i mezzi di comunicazione di massa hanno contribuito, presso un largo pubblico, ad attribuire a tali prospettive un credito maggiore di quanto la prudenza consentisse. *

Sistemi complessi

di Antonio Lepschy

fig. 1

Al fine di valutare la c. di un sistema non sembra essenziale tanto il numero delle parti che lo compongono quanto invece il modo, più o meno organico, in cui queste interagiscono. Spesso, in proposito, si ricorre a diagrammi di tipo qualitativo, come quello di fig. 1, nel quale le coordinate corrispondono ai valori di due parametri, indicati con K e con C.

Il parametro K dà conto di come il sistema evolve nel tempo e, in particolare, della possibilità o meno di prevedere tale evoluzione su intervalli più o meno lunghi, partendo da dati affetti da qualche incertezza. Per K=0 il comportamento del sistema è perfettamente prevedibile (caso dei sistemi statici o, meno banalmente, di sistemi che evolvono secondo leggi deterministiche semplici); per valori di K molto elevati l'informazione sullo stato delle singole parti si perde molto rapidamente e ciò rende impossibile, se non in termini statistici, la previsione dello stato di tali parti, noto quello all'istante t₀, anche in un istante t₁ che disti da t₀ di un intervallo molto breve. Nel diagramma di fig. 1, il punto a, caratterizzato da un valore di K prossimo a 0, può corrispondere al sistema Sole-Terra, nel quale la posizione e la velocità della Terra sono agevolmente determinabili, a partire dai valori che tali grandezze hanno nell'istante t₀, anche per valori di t₁ tali che t₁-t₀ sia da considerare piuttosto grande, pur in presenza di incertezze sui valori in t₀. Invece il punto c, caratterizzato da un valore elevato di K, può corrispondere a un gas perfetto in situazione di massima entropia, nel quale minime incertezze sui valori di posizione e di velocità delle singole molecole in un istante t₀ rendono inaccettabili le stime di tali valori dopo un intervallo anche brevissimo, a causa degli urti fra molecole, che hanno luogo in corrispondenza a certe condizioni iniziali e non avvengono, invece, per condizioni iniziali anche pochissimo diverse. Valori intermedi di K possono corrispondere ai fenomeni del caos deterministico, di cui si parlerà più innanzi.

Il parametro C dà invece conto dell'organizzazione del sistema, e cioè della struttura secondo la quale le varie parti componenti si influenzano reciprocamente, consentendo un comportamento caratterizzato da scelte funzionali al conseguimento di obiettivi, anche in presenza di più obiettivi incompatibili. Il valore più elevato di C, fra i sistemi a noi noti, si ha nel caso del cervello umano, rappresentato convenzionalmente, nella fig. 1, dal punto b.

A proposito del diagramma si può notare che né a K né a C è agevole attribuire, per un singolo sistema, un ben preciso valore (e per tale motivo si è parlato di diagramma qualitativo) ancorché sia ragionevolmente possibile, confrontando due sistemi, dire se il valore di C (o di K) di uno di essi sia superiore o inferiore al valore dello stesso parametro per l'altro sistema. Per es., una galassia, il sistema immunitario del sangue, un batterio sono caratterizzati da valori crescenti sia di C sia di K che ne collocano i punti rappresentativi sul diagramma di fig. 1 fra il punto a e il punto b (nell'ordine in cui li si è nominati). In definitiva si può dire che è soprattutto il parametro C che appare particolarmente idoneo a caratterizzare la c., nel senso in cui la si considera in questa sede.

All'aumentare del numero delle parti che compongono un sistema, generalmente K aumenta, mentre si può avere un incremento di C, a parità di numero di parti componenti, in conseguenza di una modifica della struttura del sistema che lo porti a un'organizzazione meglio articolata; peraltro valori elevati di C possono essere conseguiti solo se il numero delle parti componenti non è troppo basso.

Si può dunque concludere che è il carattere organico dei collegamenti fra le varie parti del sistema, più che il numero di queste, a dar conto della possibilità che emergano aspetti del comportamento nuovi rispetto a quelli di sistemi formati da uno stesso numero di componenti (dello stesso tipo) ma collegati fra loro in modi diversi e meno organici. Ciò suggerisce di utilizzare la nozione di emergenza per caratterizzare la c., dando così un significato concreto alla nota frase che compendia il punto di vista olistico nella formula "il tutto è più della somma delle parti". Già B. Bolzano (1851; trad. it. 1965, pp. 134, 135), nei Paradoxien des Unendlichen, si chiedeva: "Una proprietà che manca in tutte le parti deve anche non appartenere al tutto?", affermando, in risposta: "È piuttosto esattamente il contrario! Ogni tutto ha e deve avere molte proprietà che mancano alle parti".

Complessità e retroazione

Un primo livello, certamente molto elementare, di c. si manifesta nei sistemi che presentano un anello di retroazione (feedback).

Per illustrare questo concetto si farà riferimento a semplici sistemi orientati (e cioè sollecitati da 'ingressi', in risposta ai quali variano grandezze, dette 'uscite', che caratterizzano il comportamento del sistema dal punto di vista che interessa). Se il valore assunto dall'uscita in ciascun istante dipende solo dal valore dell'ingresso in quello stesso istante, il sistema viene detto non dinamico (o anche statico, o istantaneo); se invece quel valore dell'uscita dipende dall'andamento dell'ingresso anche in altri istanti, il sistema si dice dinamico (e, in particolare, causale, se l'uscita dipende solo dall'andamento passato dell'ingresso e, corrispondentemente, il valore assunto dall'ingresso in un dato istante influenza soltanto il valore futuro dell'uscita e non quello passato).

Nel caso dei sistemi dinamici, a tempo continuo, lineari e a parametri costanti nel tempo (o tempo-invarianti), detta y(t) l'uscita e u(t) l'ingresso - che qui si considereranno per semplicità scalari - il comportamento del sistema può essere descritto, in termini di legami ingresso-uscita, dall'equazione differenziale (lineare, ordinaria e non omogenea):

formula [

1]

o, in termini di rappresentazione di stato, dalle:

formula [

2]

dove x(t) è il 'vettore di stato' (di n componenti), A è una matrice, B è un vettore colonna e C è un vettore riga (da non confondere con il parametro C usato in precedenza). Sostanzialmente le [2] mostrano come il valore assunto dallo stato nell'istante t e il valore dell'ingresso nello stesso istante influenzino la tendenza a variare dello stato (e cioè il valore della sua derivata rispetto al tempo) e come l'uscita y(t) dipenda, tramite il vettore C, dal valore assunto nello stesso istante dallo stato x.

Ai fini delle considerazioni che seguono ci si può limitare allo studio della 'evoluzione libera' (a partire da condizioni iniziali non tutte nulle), e cioè al caso in cui u(t)=0, e si ha una sola situazione di equilibrio: quella in cui, nella [1], i valori della y e di tutte le sue derivate sono nulli e, nelle [2], sono nulle tutte le componenti di x. La situazione è detta 'di equilibrio' perché il sistema, se vi si trova, può permanervi indefinitamente.

L'evoluzione libera a partire da un punto diverso da quello di equilibrio è una combinazione di 'modi' del tipo e^αit corrispondenti alle radici reali α_i dell'equazione caratteristica del sistema det(sI-A)=0 e di coppie di modi e^αit sinβ_it e e^αit cosβ_it corrispondenti alle coppie di radici complesse α_i±jβ_i della stessa equazione (eventualmente moltiplicati per un polinomio in t, in caso di radici multiple).

fig. 2

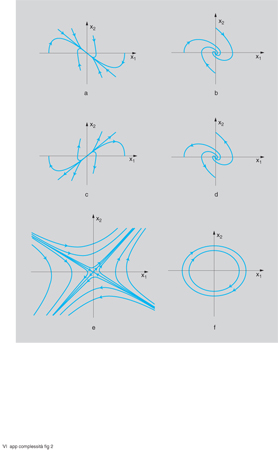
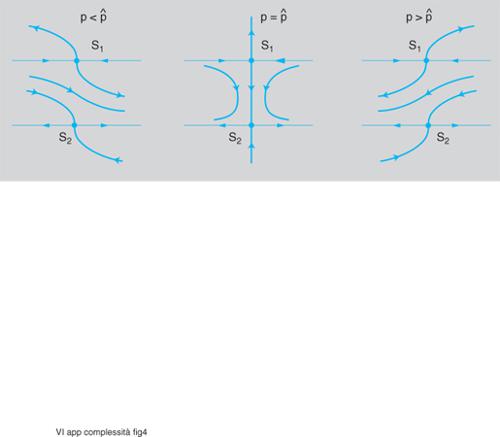
All'aumentare del valore di n (ordine del sistema) aumenta il numero dei modi, che però rimangono sempre dei due tipi considerati (i quali si possono manifestare anche in un sistema del secondo ordine: n=2). Tali modi (oltre che con il loro diagramma in funzione del tempo) sono spesso rappresentati nel quadro di fase, e cioè sul piano di coordinate x₁=y e x₂=dy/dt, il cui andamento qualitativo è riportato in fig. 2 per le sei configurazioni tipiche di nodo stabile e instabile, fuoco stabile e instabile, sella e centro.

fig. 3

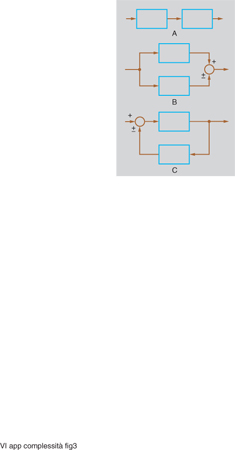
Se si collegano fra loro due (sotto)sistemi lineari a un ingresso e a un'uscita in modo da formare un nuovo sistema lineare (anch'esso a un solo ingresso e a una sola uscita), consentendo di sommare o sottrarre grandezze di ingresso e/o di uscita (ma non di moltiplicarle o dividerle fra loro), gli schemi possibili risultano quelli di fig. 3.

Nei primi due (combinazione in cascata e in parallelo o antiparallelo) i modi del sistema risultante rimangono quelli dei due sistemi componenti. Eventualmente qualche modo può sparire per cancellazione o compensazione; inoltre nella combinazione in cascata, se una radice dell'equazione caratteristica relativa a uno dei due sottosistemi coincide con una radice relativa all'altro sottosistema, nel sistema complessivo la molteplicità della radice in questione risulta uguale alla somma delle molteplicità relative ai singoli sottosistemi, e quindi il modo complessivo non coincide esattamente con quelli delle singole parti, dato che il fattore trascendente, che rimane lo stesso, è moltiplicato per un polinomio di grado diverso.

Invece nel terzo tipo di collegamento (in cui è presente un anello di retroazione positiva o negativa) i modi del sistema complessivo risultano diversi da quelli dei sottosistemi componenti: siamo allora in presenza di un anello di retroazione. Anche se le parti componenti presentano dinamiche molto semplici, addirittura tutte dello stesso tipo (come quelle legate a fenomeni di accumulo, per i quali l'uscita è l'integrale dell'ingresso), ciò non di meno il sistema complessivo presenta modi diversi da quelli delle singole parti e di tutti i tipi illustrati in fig. 2 (cioè con punti di equilibrio a nodo stabile o instabile, a fuoco stabile o instabile, a sella o a centro). In questo senso si può dire quindi che emerge un comportamento del sistema complessivo che si può considerare nuovo rispetto a quello delle parti componenti, a differenza di quanto avviene, invece, in configurazioni nelle quali non siano presenti anelli di retroazione. Ci si trova dunque di fronte a un primo livello di c., come del resto aveva già intuito nel 1948 N. Wiener individuando nel controllo a retroazione uno degli aspetti fondamentali della cibernetica, da lui definita, appunto, come la scienza che si occupa del controllo e della comunicazione non soltanto nelle macchine ma anche negli esseri viventi (caratteristica tipica dei quali è indubbiamente la c.); analogamente J.W. Forrester, in un suo noto saggio (1971) sul comportamento anti-intuitivo dei 'sistemi complessi', attribuisce questa loro caratteristica appunto alla presenza di anelli di retroazione.

Gli schemi a retroazione hanno trovato i loro impieghi pratici più tipici nella tecnica, soprattutto per scopi di controllo automatico (che determinano l'azione da esercitare sull'uscita in base allo scostamento che essa presenta rispetto a un ingresso di riferimento); vale però la pena di ricordare anche quelli nel campo della matematica applicata, per il potenziamento delle possibilità di calcolo automatico consentito dalla presenza di anelli di retroazione nel diagramma di flusso di un algoritmo (e anche, per lungo tempo, negli schemi per la soluzione 'analogica' di un'equazione differenziale). Notevole interesse presenta anche il ricorso a schemi a retroazione per lo sviluppo di modelli esplicativi (e talora anche di modelli predittivi) in varie scienze della natura, dell'uomo e della società. Prescindendo da ovvie considerazioni sul carattere 'a retroazione' di leggi fisiche, quali la legge di Lenz dell'elettromagnetismo e quella di Le Chatelier della chimica fisica, ci si limiterà qui a ricordare i modelli a retroazione relativi all'omeostasi degli esseri viventi e quelli relativi alla dinamica delle popolazioni (v. oltre), nonché i modelli macroeconomici di Samuelson-Hicks e di Phillips e quelli di Lanchester e di Richardson sui conflitti militari e sulla corsa agli armamenti.

Gioverà tuttavia tener presente che modelli puramente lineari hanno possibilità intrinsecamente limitate e che, per dar conto di alcuni aspetti importanti dei fenomeni da rappresentare, è giocoforza introdurre alcune non linearità (come, di fatto, avviene già in alcuni dei modelli ora citati o, quanto meno, in loro versioni più sofisticate).

Complessità e non linearità

Si passerà quindi a prendere in considerazione un'ulteriore possibile causa dell'emergere di nuovi tipi di comportamento, qual è quella che si ha con il manifestarsi di fenomeni non lineari, e cioè nel caso in cui quanto meno la prima delle equazioni [2] (con u(t)=0) va sostituita con un'equazione del tipo

formula [

3]

In questa sede ci si limiterà a considerare funzioni f sufficientemente regolari, in particolare continue assieme alle loro derivate fino a quella di ordine k, con k ed n (dimensione di x) piuttosto modesti.

Nel caso lineare (con la matrice A non singolare) si aveva un solo punto di equilibrio in x=0 e questo, in un sistema del secondo ordine, poteva essere soltanto dei tipi indicati in fig. 2. La [3], invece, può avere più punti di equilibrio. Detto ˆx uno di essi (per il quale si ha f(ˆx)=0), in luogo della [3] si può considerare l'equazione linearizzata (valida in un intorno di ˆx):

formula [

4]

in cui J(ˆx) è la matrice jacobiana della f(x), calcolata per x=ˆx e svolge una funzione analoga a quella della matrice A in [2]; per altro non tutte le informazioni che la A fornisce in maniera univoca sul comportamento di un sistema lineare possono essere ottenute dalla J(ˆx) per quanto riguarda il comportamento del sistema non lineare, sia pure limitatamente all'intorno di ˆx; infatti se tutti gli autovalori di J(ˆx) hanno parte reale negativa o se, viceversa, almeno uno di essi ha parte reale positiva, anche il punto di equilibrio del sistema non lineare presenterà caratteristiche di stabilità (tutte le traiettorie convergono su ˆx) o, rispettivamente, di instabilità (vi sono traiettorie che divergono da ˆx, anche se prendono origine da un punto molto vicino a quello di equilibrio); se però, per es., in un sistema del secondo ordine, si ha una coppia di autovalori di J(ˆx) con parte reale nulla (nel qual caso il sistema linearizzato presenta un centro in ˆx), il sistema non lineare, nell'intorno di ˆx, esibisce un quadro di fase che può corrispondere a quello di un centro, ma può altresì avere le caratteristiche di un fuoco stabile oppure di un fuoco instabile.

Un altro aspetto di comportamento nuovo, che emerge in presenza di non linearità (anche non drastiche), consiste nell'esistenza di insiemi limite diversi dai punti di equilibrio. Gli insiemi limite più comuni sono i cicli e i tori; accanto a questi si possono considerare anche le linee omocline, che escono da un punto sella e vi ritornano seguendo una traiettoria diversa da quella del modello linearizzato a causa della deformazione di una delle due traiettorie che escono dal punto sella (cfr. fig. 2); tale deformazione, dovuta alla non linearità della f(x), produce un ripiegamento della traiettoria, fino a farla diventare una delle due traiettorie che, nel modello linearizzato, entrano nel punto sella.

I cicli limite si possono avere in sistemi almeno del secondo ordine (n∙2) e corrispondono a traiettorie chiuse (e quindi a oscillazioni persistenti) di forma non necessariamente ellittica e, pertanto, la corrispondente evoluzione nel tempo è periodica ma non necessariamente sinusoidale. Il ciclo limite si distingue in modo essenziale dalle oscillazioni che si hanno intorno a un centro, perché queste ultime possono essere di qualsiasi ampiezza mentre i cicli limite sono traiettorie chiuse isolate: nel caso di cicli stabili le traiettorie che partono da punti non appartenenti al ciclo (in un suo conveniente intorno) convergono su di esso, mentre in quello dei cicli instabili ne divergono.

Da un punto di vista 'fisico', l'insieme delle infinite curve chiuse intorno a un centro corrisponde al comportamento (ideale) di un pendolo senza attriti (o, in campo elettrico, di un circuito risonante LC di resistenza nulla); un ciclo limite, invece, corrisponde a fenomeni più complessi in cui una sorgente di potenza fornisce, in ciascun periodo, l'energia dissipata (come avviene, per il contributo della molla o dei pesi, in un orologio a pendolo o, per quello dei componenti attivi, in un oscillatore elettronico); in tal caso l'oscillazione generata (almeno a regime) è di ampiezza (oltre che di frequenza) costante e può avere varie forme (per es., quelle di un'onda quadra o di un'onda 'a dente di sega', fino a quelle, assai complesse, del battito cardiaco e del segnale elettrocardiografico, anche se, per questi ultimi segnali, sembrano meglio adatti modelli più sofisticati di un ciclo limite; v. oltre).

In un sistema con n uguale almeno a 4 si possono avere due oscillazioni; se il loro rapporto è razionale, si ha ancora un ciclo limite (una curva unidimensionale chiusa che si sviluppa nello spazio a quattro dimensioni); se però il loro rapporto è irrazionale, l'insieme limite diventa una curva aperta dello spazio a quattro dimensioni, i cui punti possono essere messi in corrispondenza biunivoca con quelli di una superficie torica di uno spazio a tre dimensioni; lungo tale superficie torica l'immagine della traiettoria considerata si avvolge a elica, ricoprendola densamente, senza ripassare mai una seconda volta per un punto già toccato.

Punti di equilibrio, cicli limite e tori costituiscono, come si è detto, le forme più semplici e comuni di insieme limite. Se tutte le traiettorie che escono da punti del loro intorno tendono a essi, tali insiemi limite si dicono attrattori; se invece le traiettorie tendono ad allontanarsi dall'insieme limite, pur partendo da punti molto prossimi a esso, l'insieme limite è detto repulsore; chiaramente l'attrattore di un dato sistema non lineare coincide con un repulsore per il sistema non lineare che funziona 'a tempo invertito' rispetto al sistema considerato. Vi sono poi anche insiemi limite che non sono né attrattori né repulsori, com'è, per es., il caso di un ciclo limite (appartenente a un piano) in cui le traiettorie che partono da punti al suo interno tendono a esso, mentre quelle che partono da punti esterni se ne allontanano (o viceversa). Uno stesso sistema non lineare può presentare più attrattori e repulsori; tipico è il caso, in un sistema del secondo ordine, di un punto di equilibrio stabile circondato da un ciclo limite instabile, a sua volta circondato da un ciclo limite stabile, e così via. Il primo ciclo limite instabile racchiude il 'bacino di attrazione' del punto di equilibrio stabile; la regione anulare compresa fra due cicli limite instabili consecutivi costituisce il bacino di attrazione del ciclo limite stabile compreso fra di essi.

Fenomeni complessi legati all'influenza di parametri

Ulteriori aspetti del comportamento del sistema emergono se, in luogo della [3], si considera l'espressione

formula [

5]

dove p è un vettore le cui componenti possono essere interpretate come parametri che influenzano i coefficienti delle equazioni del sistema. Si noti che p, nella [5], non è una funzione del tempo (come lo è invece la u(t) nella [1] o nelle [2]), e infatti l'analisi della [5] viene condotta valutando, nello spazio dei parametri, cioè per ogni valore (vettoriale) di p, non tanto l'evoluzione nel tempo dello stato x, quanto gli aspetti complessivi del comportamento del sistema, quali la presenza o meno di determinati insiemi limite e le loro caratteristiche di attrattori o repulsori (anche se, in caso di variazioni di p che risultino 'lente' in rapporto ai tempi caratteristici che compaiono nella dinamica del sistema, l'analisi considerata può essere valida anche per lo studio dell'evoluzione temporale dello stato x, dal momento che, nelle ipotesi fatte, in ciascun intervallo di durata significativa per l'evoluzione di x(t) il parametro p subisce variazioni modeste e può essere ragionevolmente approssimato con il suo valore medio nell'intervallo stesso).

Lo spazio che ha come coordinate sia i valori di ciascuna componente di x sia quelli di ciascuna componente di p viene detto spazio di controllo; un esempio particolarmente semplice è quello dello spazio di controllo a tre dimensioni relativo a un sistema del secondo ordine (n=2), che dipende da un parametro scalare; in ogni piano ortogonale all'asse corrispondente ai valori di tale parametro si sviluppano le traiettorie (quadro di fase) del sistema (a parametri costanti) nelle cui equazioni il valore del parametro p coincide con la 'quota' del piano considerato.

La denominazione di spazio di controllo è relativa all'interpretazione che se ne dà in rapporto alla possibilità di far variare i coefficienti dell'equazione (e, quindi, la dinamica del sistema) modificando il parametro p, per es. secondo una funzione del tempo costante a tratti: se, con p=p₀ , il sistema evolve a partire dallo stato x₀ e all'istante t₁, in cui lo stato ha assunto il valore x₁, si modifica il valore del parametro da p₀ a p₁, nell'intervallo successivo lo stato evolve, a partire dal valore x₁, secondo una legge diversa da quella che sarebbe stata seguita se il parametro avesse conservato il valore p₀. Si può così imporre alla traiettoria dello stato la forma di una spezzata di archi consecutivi che approssimi un andamento desiderato, non compatibile con l'evoluzione libera del sistema per nessun valore (costante) di p.

Si noti che il termine 'controllo' è usato anche, con riferimento alle equazioni [1] e [2], per designare l'ingresso u(t), che pure modifica l'evoluzione dello stato rispetto a quella che si avrebbe per u(t)=0. Una certa analogia fra gli effetti dei due modi di influire sull'andamento di x(t) e, quindi, anche dell'uscita y(t), giustifica l'uso della parola 'controllo' per entrambi i casi e, tuttavia, se di tale analogia si desse un'interpretazione troppo estensiva, la cosa potrebbe essere fonte di equivoci.

Con riferimento allo spazio dei parametri si parla di stabilità strutturale (di una data regione di tale spazio) se all'interno di essa il comportamento del sistema rimane qualitativamente dello stesso tipo (per es., un nodo stabile rimane un nodo stabile, un ciclo rimane un ciclo ecc.). All'interno di ciascuna di tali regioni di stabilità strutturale, quindi, il comportamento del sistema non presenta alcun aspetto sostanzialmente nuovo rispetto a quanto emerge dall'analisi della [3] attribuendo ai suoi coefficienti valori corrispondenti a un qualsiasi punto della regione considerata dello spazio dei parametri.

Novità sostanziali emergono invece nei punti di frontiera di tali regioni, detti punti di biforcazione, perché nel loro intorno si hanno punti dello spazio dei parametri arbitrariamente vicini fra loro, cui corrispondono sistemi dinamici, descritti da equazioni del tipo della [3] con caratteristiche essenzialmente diverse fra loro (per es., in uno dei due sistemi si manifesta un ciclo limite che nell'altro non appare, oppure si modifica la natura di un punto di equilibrio).

Le biforcazioni possono essere locali o globali. Le biforcazioni locali si possono avere anche in sistemi lineari, descritti da equazioni del tipo della [2] per u(t)=0; esse corrispondono a valori critici degli autovalori della matrice A (o di quelli della matrice Jacobiana J(ˆx) nel caso della [3]): per es., se, per un certo valore del parametro, la parte reale di due autovalori complessi coniugati è nulla, per valori del parametro vicinissimi a quello considerato gli autovalori possono avere parte reale negativa e, rispettivamente, positiva e in tal caso il punto di equilibrio passa da fuoco stabile, a centro, a fuoco instabile. Nel caso di sistemi non lineari, inoltre, si possono avere collisioni di insiemi limite (per es., in corrispondenza a un ben definito valore di p, un ciclo limite stabile e un ciclo limite instabile collidono in un solo ciclo, tale che le traiettorie uscenti da punti molto prossimi a tale ciclo convergono su di esso nel caso dei punti interni e se ne allontanano in quello dei punti esterni, o viceversa).

fig. 4

Le biforcazioni globali, invece, corrispondono non a valori critici degli autovalori della matrice jacobiana ma a un'alterazione complessiva del quadro di fase; ne è un esempio la fig. 4, che rappresenta, per il caso di un parametro scalare p, l'andamento delle traiettorie per p〈ˆp, p=ˆp e p>ˆp: in tutti e tre i casi si hanno sempre due punti sella S₁ ed S₂, nell'immediato intorno dei quali la situazione non si modifica in modo sostanziale; però per p=ˆp si ha un'eteroclina che collega i due punti sella, separando drasticamente la regione alla sinistra e quella alla destra dell'eteroclina stessa, mentre negli altri due casi si ha una sorta di 'corridoio' nel quale le traiettorie vanno da sinistra verso destra se p〈ˆp e da destra verso sinistra per p>ˆp (i tre quadri di fase possono essere interpretati, come si è detto, come tre sezioni ortogonali all'asse p nello spazio di controllo di coordinate x₁, x₂, p).

Tra le biforcazioni locali più note si citano quelle di collisione fra punti di equilibrio (per es., nodo-sella), quella di Hopf (collisione fra un punto di equilibrio e un ciclo), quella 'tangente' e quella di flip (collisioni fra cicli), quella di Naimark-Sacker (collisione fra un ciclo e un toro). Tra le biforcazioni globali la più significativa è quella già citata di collisione tra una traiettoria uscente da una sella e una traiettoria entrante in un'altra sella (o anche nella stessa sella: omoclina).

La perdita di stabilità strutturale caratteristica delle biforcazioni ha suggerito di utilizzarle come modelli (esplicativi o anche predittivi) per molti fenomeni della fisica e della tecnica (interpretazione del carico di punta della scienza delle costruzioni come una biforcazione 'a forcone'), della biologia, dell'ecologia (il modello 'predatore-preda' di Rosenzweig utilizza la biforcazione di Hopf), dell'economia; una situazione particolarmente semplice (in quanto si presenta anche in uno spazio di controllo bidimensionale: n=1, p scalare) è quella legata all'interpretazione dei fenomeni di isteresi (essa, fra l'altro, consente un'interpretazione soddisfacente del battito cardiaco).

Nello studio dei fenomeni di perdita della stabilità strutturale si è fatto largo impiego di nozioni della teoria delle catastrofi (v. catastrofi, Teorema delle, App. V). Una biforcazione è infatti catastrofica (cioè comporta una ristrutturazione sostanziale dell'equilibrio: si ricorda che nella letteratura scientifica in lingua russa è spesso usata la parola perestrojka, nel senso di ristrutturazione o metamorfosi) quando, nel caso di un parametro scalare p, se si passa da un valore p_a a un valore p_b, ad esso arbitrariamente 'vicino' ma separato da un valore critico p₀, da ogni punto x₀ di un opportuno insieme si evolve verso un attrattore macroscopicamente 'lontano' da quello verso il quale si evolveva per p=p_a. Ovviamente non tutte le biforcazioni sono catastrofiche; in quelle non catastrofiche l'attrattore cui si tende per p=p_b è vicino a quello cui si tende per p=p_a; si hanno, inoltre, anche biforcazioni indeterminate, nelle quali da alcuni x₀ dell'intorno considerato si tende a un attrattore 'vicino' e da altri a un attrattore 'lontano' da quello cui si tende (per tutti i valori di x dell'insieme considerato) per p=p_a.

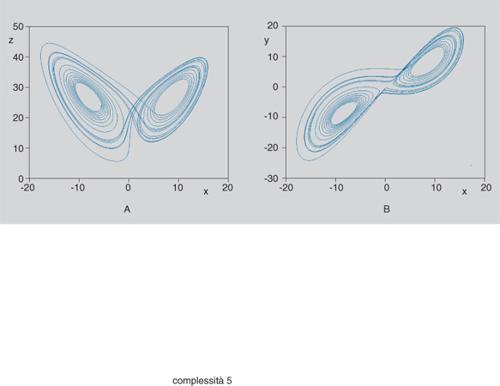
Attrattori strani. - All'aumentare dell'ordine n del sistema (e cioè delle dimensioni del vettore di stato) emergono nuovi fenomeni di caratteristiche più complesse in corrispondenza all'apparire di attrattori strani, cioè di insiemi limite 'attrattivi' sostanzialmente diversi dai punti di equilibrio, dai cicli e dai tori stabili. Per tale tipo di attrattori non si dispone di una definizione precisa che sia, nel contempo, accettata da tutti: troppo vaga è, probabilmente, quella negativa di cui si è fatto uso (basata sulla loro sostanziale differenza rispetto ai punti di equilibrio, ai cicli o ai tori); certamente suggestive ma, sotto qualche aspetto, forse troppo limitative sono quelle che li caratterizzano in base alla forte sensibilità alle condizioni iniziali e alla dimensione frattale.

fig. 5

Un attrattore strano (uno dei più semplici e più noti è l'attrattore di Lorenz, schematizzato in fig. 5) è generalmente confinato in una regione limitata dello spazio di stato, mentre il suo bacino di attrazione occupa una regione assai più estesa (talora l'intero spazio). Dai punti del bacino di attrazione esterni alla regione dell'attrattore evolvono traiettorie che si dirigono verso di esso in modo non troppo diverso da quello con il quale tenderebbero a un attrattore di tipo più semplice; quando però la traiettoria entra nella regione dell'attrattore, essa evolve in modo sostanzialmente diverso da quello che caratterizza i cicli e i tori.

Più precisamente, due traiettorie passanti per punti molto vicini (per es., tali che la loro distanza sia inferiore all'inevitabile errore di misura) continuano a essere vicine fuori dalla regione dell'attrattore ma, una volta giunte in essa, si allontanano ben presto notevolmente l'una dall'altra, tanto che il punto di una di esse, in un dato istante, può trovarsi prossimo alla frontiera della regione che include l'attrattore mentre il punto dell'altra, nello stesso istante, si può trovare al centro della regione o anche in un punto diametralmente opposto a quello del primo. Poiché la regione dell'attrattore è limitata, i punti corrispondenti a uno stesso istante sulle due traiettorie dovranno poi inevitabilmente riavvicinarsi, e poi allontanarsi di nuovo ma senza dar luogo a un comportamento periodico o quasi periodico.

fig. 6

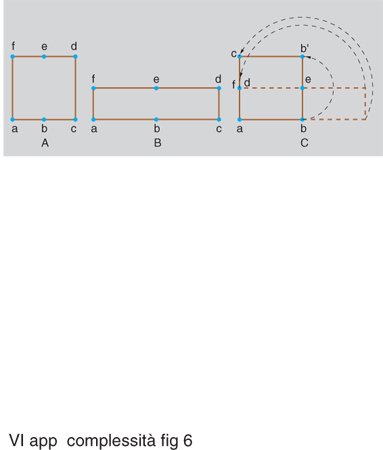
Questa caratteristica delle traiettorie viene spesso interpretata come effetto dell'alternarsi delle due azioni di stretching (stiratura) e di folding (ripiegamento), a proposito delle quali si usa spesso l'espressione di 'trasformazione del fornaio', perché ricordano le operazioni compiute sulla farina con l'acqua (e gli eventuali altri ingredienti) per formare l'impasto da destinare alla cottura. La fig. 6 illustra, per il caso bidimensionale, gli effetti successivi delle due operazioni eseguite su un insieme di punti di forma iniziale quadrata (precisamente un quadrato aperto, privo del suo perimetro): lo stretching deforma il quadrato in un rettangolo (nel caso del disegno, di base doppia e altezza dimezzata); il folding ripiega la metà destra del rettangolo sopra la metà sinistra, facendola ruotare intorno al punto e. Si arriva così di nuovo a un quadrato in cui però punti inizialmente 'lontani' come quelli prossimi ad a e, rispettivamente, a f divengono molto 'vicini', mentre punti inizialmente 'vicini' (come quelli prossimi ad a e, rispettivamente, a b) vengono allontanati.

Nel caso di comportamenti di questo tipo si parla abitualmente di caos deterministico (v. anche caos e complessità, App. V): infatti il sistema è rigidamente deterministico (in quanto retto da equazioni del tipo della [3], senza alcun elemento stocastico legato a variazioni di parametri o a sollecitazioni esterne descrivibili in termini probabilistici) e, ciò non di meno, il comportamento del sistema appare 'caotico' (nel senso di imprevedibile) in quanto minime incertezze nella valutazione dello stato presente si traducono ben presto in differenze molto elevate dello stato futuro (pur in assenza di divaricazioni crescenti delle traiettorie, quali si hanno nei sistemi instabili, dato che l'attrattore è racchiuso in una regione limitata).

I principali meccanismi di passaggio al caos per modifiche graduali dei valori di parametri di sistemi non caotici sono, fondamentalmente, una cascata di biforcazioni locali (detta cascata di Feigenbaum) oppure una sola biforcazione, ma di carattere globale (caos omoclino, nel caso si abbia una sola sella, caos eteroclino, se si hanno almeno due selle).

Per quanto riguarda la geometria frattale degli attrattori strani, questa si rivela, fondamentalmente, in due aspetti: mentre gli attrattori 'tradizionali' hanno dimensione intera (il cui valore è 0 per i punti di equilibrio, 1 per i cicli limite, 2 per i tori), molti attrattori strani presentano una dimensione espressa da un numero non intero; inoltre, in molti casi, si ha anche il ripetersi di caratteristiche qualitative simili a vari livelli di scala.

Come si è visto, si manifestano fenomeni sostanzialmente nuovi e, quindi, emergono aspetti di comportamento che autorizzano a parlare di successivi livelli di c.: quando si ricorre a combinazioni in retroazione (feedback) con le quali gli autovalori del sistema lineare complessivo risultano diversi da quelli delle parti componenti; quando si sostituiscono, a relazioni lineari, relazioni non lineari per effetto delle quali si manifestano insiemi limite, attrattori o repulsori, diversi dai classici punti di equilibrio dei sistemi dinamici lineari; quando variazioni di parametri provocano la comparsa di fenomeni di biforcazione alle frontiere delle regioni di stabilità strutturale; infine quando si manifestano le tipologie più complesse di attrattori che danno luogo alla comparsa del caos deterministico.

bibliografia

B. Bolzano, Paradoxien des Unendlichen, Leipzig 1851 (trad. it. Milano 1965).

L. von Bertalanffy, General system theory, New York 1968 (trad. it. Milano 1983).

J.W. Forrester, Principles of systems, Cambridge (Mass.) 1968.

J.W. Forrester, Counterintuitive behavior of social systems, in Technology review, 1971, pp. 52-68.

V.I. Arnol´d, Geometrical methods in the theory of ordinary differential equations, New York 1983, 1988².

J. Guckenheimer, P. Holmes, Nonlinear oscillations, dynamical systems, and bifurcations of vector fields, New York 1983.

La sfida della complessità, a cura di G. Bocchi, M. Ceruti, Milano 1985.

G. Nicolis, I. Prigogine, Die Erforschung des Komplexen: auf den Weg zu einem neuen Verständnis der Naturwissenschaften, München 1987 (trad. it. La complessità - esplorazione di nuovi campi della scienza, Torino 1991).

R.Calimani, A. Lepschy, Feedback, Milano 1990.

S. Wiggins, Introduction to applied nonlinear dynamical systems, and chaos, New York 1990.

S. Rinaldi, Stabilità strutturali e biforcazioni e Il caos deterministico, in Biosistemi e complessità, a cura di E. Berardinelli, S. Cerruti, Bologna 1993.

Complessità biologica

di Saverio Forestiero

I sistemi viventi della biosfera vengono di norma ordinati in una gerarchia di entità, ciascuna delle quali vuole rappresentare un livello di organizzazione della materia vivente. Cellula, organismo pluricellulare, popolazione, comunità ecologica sono oggetti biologici tipicamente graduati secondo un criterio di complessità crescente.

Per molti anni la c. è sembrata essere un attributo, seppure non esclusivo, tuttavia così inerente i sistemi viventi da venire percepito come un fatto talmente ovvio, come un dato di osservazione talmente evidente da non meritare un'attenzione teorica particolare. Questa assunzione acritica dell'autoevidenza della c. dei viventi ha avuto come principali conseguenze, da una parte, l'ontologizzazione della c. biologica e, dall'altra, la mancanza di una definizione chiara ed esaustiva di c. biologica che fosse fondata sui risultati di ricerche specifiche, sperimentali o teoriche.

Negli ultimi anni Novanta, più cautamente, pur rimandando al futuro il compito di formulare una definizione scientifica di c. biologica, si è cominciato a guardare a essa come a un attributo non tanto dei sistemi viventi in se stessi, quanto, piuttosto, delle rappresentazioni che dei sistemi viventi dà la scienza. Intrinsecamente complessi sarebbero perciò i modelli della conoscenza biologica e non gli oggetti del mondo biologico. Tra le tante conseguenze collegabili a questo mutamento di ottica se ne indicano in questa sede due sole. In primo luogo l'attribuire la c. ai modelli di rappresentazione, sottesi dalla relazione osservatore-osservato, piuttosto che agli oggetti in se stessi, rimuove dall'attività di ricerca le eventuali preclusioni di ordine metafisico, rendendo i sistemi viventi conoscibili anche in via di principio. In secondo luogo, la c. pone i modelli biologici come in larga misura irriducibili alle spiegazioni classiche nell'ambito delle scienze fisiche, formulate in termini matematici, in cui la c. sembra essere invece marginale.

Rimanendo nel solco di una visione tradizionale, epistemologicamente discutibile, ma ancora largamente condivisa sul piano linguistico-comunicativo, visione che attribuisce la c. ai sistemi viventi piuttosto che alla modellizzazione che di loro dà la scienza, potremmo dire che il carattere intrinsecamente complesso dei sistemi viventi concorre a fondare l'autonomia della biologia e a mutare i caratteri definitori della conoscenza scientifica. L'idea di scienza basata sul modello proprio delle scienze quantitative, nomologiche e assiomatizzabili, sembra oggi in via di revisione: essa si modifica e si amplia per accogliere quei metodi e quelle procedure proprie della conoscenza imperfetta, solitamente non matematizzabile e assai raramente predittiva che caratterizza le scienze della vita.

Fondamenti della complessità biologica

L'organizzazione, l'individualità, la diversità, la relazionalità sono quattro caratteristiche comuni ai sistemi viventi e ne determinano la complessità.

Organizzazione. - Una proprietà fondamentale di tutti i viventi è quella di essere sistemi organizzati. Possedere un'organizzazione significa presentare un certo insieme di relazioni che assicurano la coerenza interna del sistema. Queste relazioni sono responsabili dell'unitarietà di ogni sistema vivente e della sua tenuta.

L'organizzazione dei viventi mostra di avere una natura gerarchica per cui gli organismi unicellulari, quelli pluricellulari, le popolazioni e le biocenosi si presentano come entità fenomeniche caratterizzate da configurazioni strutturali e da dinamiche processuali differenti a ciascun livello e dotate di proprietà né immediatamente deducibili né prevedibili. Oltre che gerarchica tale organizzazione è anche chiusa, grazie all'innesco di un processo di circolarità in meccanismi altrimenti lineari di causa ed effetto. La logica circolare (ben esemplificata dal rapporto causale: gameti-zigote-gameti) percorre tutti i livelli della gerarchia, dalla cellula all'ecosistema. I sistemi viventi sono sistemi chiusi rispetto alla loro organizzazione interna ma sono sistemi aperti sull'esterno, con il quale scambiano materia, energia, informazione. Ogni organismo è necessariamente connesso con l'ambiente, e tale connessione è a tal punto obbligata che diventa impossibile anche solo concepire l'esistenza di un organismo isolato oppure isolabile dal proprio ambiente.

Individualità. - I sistemi viventi non sono ripetitivi: l'eterogeneità è la norma. Tanto sul piano strutturale che su quello funzionale, i sistemi viventi sono distinguibili dai sistemi naturali non viventi sulla base della loro individualità.

Di norma ogni vivente possiede una propria individualità (una unicità originariamente dovuta alle proprietà stocastiche della sorgente di variazione) che viene codificata nei geni, viene costruita epigeneticamente e viene trasmessa alle generazioni successive. All'interno di ciascun deme (popolazione locale), la somma delle individualità si traduce nell'assetto di variazione genetica mediante cui la popolazione nel suo insieme fronteggia le pressioni dell'ambiente. L'unicità degli individui diventa essenziale per l'adattamento della popolazione a un ambiente perennemente mutevole.

La stragrande maggioranza dei sistemi viventi può essere costituita non solo da entità tra loro intrinsecamente, cioè genotipicamente, diverse, ma può anche essere formata da subunità strutturalmente eterogenee, che hanno quindi comportamenti che seguono leggi differenti l'una dall'altra. È il caso del corredo di proteine enzimatiche di una cellula (che catalizzano particolari reazioni biochimiche regolate da particolari meccanismi di controllo), o quello dei diversi tipi di cellule costitutive del corpo dei vertebrati. In sostanza la c. biologica deve essere riferita a sistemi di tipo individuale, cioè non ripetitivo, per i quali valgono dunque leggi specifiche. Da ciò deriva un'importante conseguenza di ordine teorico generale: la non universalità delle leggi ricavabili dalle descrizioni dei sistemi biologici ha reso estremamente difficile l'applicabilità dei metodi matematici di tipo deterministico ai fenomeni biologici. Un'ulteriore osservazione riguarda il fatto che l'individualità dei sistemi biologici ha duplice natura: essa è concausa di evoluzione e prodotto storico dell'evoluzione.

Diversità. - Differenze di vario ordine e grado sottostanno alla complessità. Indipendentemente dagli effetti di scala, la diversità dei sistemi viventi deriva dal-la loro individualità e concorre a definire la loro complessità. Globalmente, la diversità biologica è costituita dall'insieme delle differenze osservabili tra gli esseri viventi. Tali differenze possono essere descritte in termini di quantità, di variazione e di variabilità degli organismi; nonché, semplificando, in rapporto ai geni, alle specie e agli ecosistemi. In particolare, la diversità genetica è rappresentata da tutte le differenze ereditabili esistenti tra gli individui in una popolazione e tra le diverse popolazioni, che sono riconoscibili a livello genico.

La diversità genetica è riconducibile, in ultimo, alle differenze di sequenza nelle coppie di basi degli acidi nucleici. Negli organismi dotati di sessualità, le novità genetiche comparse per mutazione possono diffondersi nella popolazione mediante ricombinazione, cioè attraverso un dispositivo capace di generare un immenso numero di differenze. La struttura e il numero dei cromosomi, come pure la quantità di DNA contenuto in una cellula, sono esempi di diversità genetica. In particolare, la quantità di DNA contenuta in una cellula (dimensione del genoma) permette di confrontare organismi di taxa di livello anche molto superiore a quello di specie. Nei batteri, per es., le dimensioni dei genomi variano ampiamente da 6×10⁵ bp a più di 10⁷ bp. Il genoma del micoplasma è formato da circa 400 geni, mentre negli altri batteri il numero di geni varia tra 500 e 8000. La maggioranza degli eucarioti possiede, invece, qualcosa come 50.000 geni e un contenuto di DNA estremamente differente, variabile tra 8,8×10⁶ bp e 6,9×10¹¹ bp. Evolutivamente, la comparsa della sessualità ha provocato un incremento della diversità genetica e della c. dei sistemi viventi. La sua enorme diffusione tassonomica viene associata a meccanismi di riparazione del DNA e di differenziamento cellulare, e viene interpretata come meccanismo base per la produzione di varianti genetiche adattabili ai cambiamenti ambientali per via fenotipica, per l'incremento della cladogenesi e il decremento dei tassi di estinzione: in sostanza la sessualità sembra essere importante perché può agire ed essere favorita a molti livelli di organizzazione dei sistemi viventi, da quello di gene a quello di popolazione-specie.

8

9

10

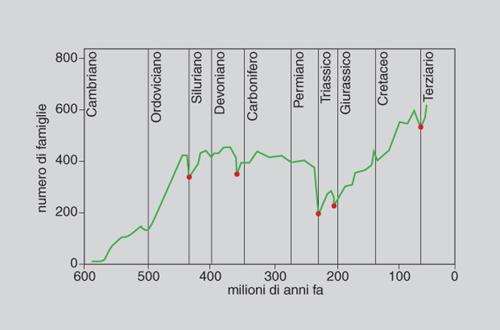
La diversità tassonomica di specie, oltre alla componente spaziale e geografica, ha una componente temporale. La diversità oggi osservabile è il risultato di un processo storico lunghissimo iniziato tra 3900 e 3400 milioni di anni fa con la comparsa della vita sul nostro pianeta. Tale processo di produzione delle differenze tra i viventi ha natura irreversibile. La ricostruzione paleontologica dimostra il fatto che la diversità macrotassonomica (intesa come ricchezza di tipi organizzativi) raggiunse il suo apice nel Cambriano, e che la diversità di famiglie e di specie è andata aumentando dal Cambriano al Pleistocene con poche battute d'arresto, in corrispondenza delle fasi, brevi e isolate, di estinzione di massa (figg. 8, 9 e 10).

Le differenze ecologiche, e quindi la complessità ecologica degli ecosistemi, sono le più difficili da definire perché di norma le comunità e gli ecosistemi sono entità dai contorni sfumati, perché gli ecosistemi non sono entità esclusivamente biologiche ma includono anche la componente abiotica, e infine perché esiste un fattore di scala spazio-temporale che influenza pesantemente l'osservazione, la misurazione e l'interpretazione delle differenze sia intra- sia inter-ecosistemiche. Spesso la diversità ecologica viene articolata su più livelli gerarchici, da quello di biocenosi a quello di ecosistema, di paesaggio, anche se vi sono dubbi che a ognuno di questi livelli corrisponda effettivamente un'entità strutturalmente e funzionalmente autonoma. Tipicamente la diversità ecologica viene caratterizzata con riferimento a tre principali componenti. La diversità alfa (α) e la diversità gamma (γ) riguardano il numero di taxa presenti, rispettivamente, alla scala locale e a quella regionale; la diversità β rappresenta l'intensità del cambiamento in specie osservato in zone di transizione tra due tipi diversi di sistemi lungo un gradiente fisiografico. La diversità β misura, attraverso indici, il livello di somiglianza tra aree prossime, la diversità ecologica tra biotopi contigui. La più semplice relazione tra queste tre componenti è tale per cui la diversità β è uguale al rapporto tra la diversità γ e la diversità α.

Il fatto che le specie di una comunità non abbiano tutte lo stesso numero di individui ma presentino differenti abbondanze è uno degli aspetti più cospicui degli ecosistemi. Per lungo tempo si è creduto che la c. strutturale degli ecosistemi potesse essere ridotta, o almeno sintetizzata, in un indice quantitativo che ne misurasse la diversità di specie, ma indagini più approfondite hanno messo in luce il fatto che così intesa la diversità non è una proprietà esclusiva delle biocenosi, ma di qualsiasi collezione di tipi eterogenei caratterizzata da abbondanze differenti. C'è invece concordanza sul fatto che nel tempo la diversità complessiva di una biocenosi cresca (anche nel caso che il numero assoluto di specie rimanga costante), a mano a mano che le abbondanze delle specie tendono a equivalersi. La c. ecologica ha anche manifestazioni funzionali coincidenti con i tipi di relazioni che intercorrono tra gli organismi di un ecosistema e i suoi processi; sono processi ecosistemici lo stoccaggio e il flusso di materiali e di energia, il mantenimento della stabilità ecologica, la ripartizione delle risorse tra le specie, nonché molti diversi comportamenti delle specie (tra i tanti, quelli collegati alla competizione, alla predazione, al parassitismo, all'impollinazione). La diversità ecologica funzionale riguarda i vari modi con cui si possono realizzare le funzioni ecologiche degli ecosistemi: a ognuno di questi differenti modi corrisponderà il tipo di organizzazione proprio di uno specifico ecosistema.

Relazionalità. - Dall'azione di forze si passa alle relazioni attraverso segnali. La possibilità, comprovata per certi sistemi non viventi (per es., il sistema fisico di H. Benard o la reazione di V.V. Belousov e A.M. Zhapotinski), di passare spontaneamente da condizioni di tipo caotico a stati di tipo ordinato ha indotto molti ricercatori a ritenere che processi analoghi fossero responsabili della c. dei sistemi viventi e del suo incremento. L'analogia tra i sistemi complessi di tipo fisico o chimico e quelli biologici è però solo superficiale. In effetti, l'azione delle forze fisiche esterne che tendono a strutturare le unità caotiche di un sistema chimico molecolare viene a mancare nei sistemi biologici. Qui, invece, l'elemento di ordine, capace di organizzare le componenti eterogenee del sistema, è rappresentato da relazioni che promuovono l'interconnessione tra le parti. Tali relazioni hanno la forma di un segnale.

Attraverso segnali le cellule di una coltura batterica o le componenti di un sistema pluricellulare trasferiscono informazioni dall'una all'altra, coordinando i processi interni con quanto accade all'esterno di ciascuna di esse. A livello degli organismi pluricellulari, il sistema costituito dal segnale e dal suo recettore non solo assicura l'integrazione tra le varie cellule, per es. durante i processi di sviluppo, ma negli animali può anche consentire l'integrazione sociale degli individui vuoi attraverso l'azione degli ormoni, vuoi attraverso quella dei neurotrasmettitori. In tutti i gruppi di organismi si assiste a una diversificazione della coppia segnale-recettore. Tale diversificazione evolutiva produce sia una complicazione del sistema, sia una sua divisione in compartimenti, con la localizzazione, in alcune regioni del corpo, delle cellule contenenti i differenti recettori. Inoltre, se da una parte l'evoluzione filogenetica della coppia segnale-recettore ha la funzione di rendere più efficiente e affidabile l'integrazione tra gli individui (con ciò aumentando la diversità interna, intrasistemica, dei sistemi viventi), dall'altra essa serve a mantenere isolati sistemi tra loro incompatibili e in competizione (favorendo così la diversità esterna, intersistemica). I segnali coinvolti nel comportamento, e responsabili della produzione delle barriere interspecifiche di isolamento riproduttivo precopula, esemplificano puntualmente la funzione di mantenimento e incremento della diversità intersistemica, e illustrano, a un livello assai elevato di c., quale sia la natura delle 'forze' che determinano la dinamica dei sistemi viventi. Negli animali dotati di un sistema nervoso e di un cervello sufficientemente complesso, il sistema segnale-recettore è ancora all'opera nel consentire l'apprendimento e dunque la generazione di più sofisticati meccanismi di produzione di diversità e di complessità. Infine, riferendosi a un altro ambito fenomenologico, è sempre la capacità relazionale dei sistemi viventi che è chiamata in causa nell'elaborazione epigenetica dell'informazione genomica nei processi di riconoscimento immunitario, nella morfogenesi, nell'ontogenesi del comportamento.

Tendenze evolutive e complessità

L'ordinamento di c. crescente, cioè cellula procariotica, cellula eucariotica, organismo pluricellulare, popolazione, comunità, ecosistema, di solito si accompagna all'idea che nella storia della vita sul pianeta sia riconoscibile una tendenza storica verso la crescita della c. dei sistemi viventi. Per quanto suggestiva, questa convinzione si dimostra errata perché se è indiscutibile che le forme organizzative più semplici hanno preceduto di norma quelle più complesse, tuttavia la coesistenza temporale di forme poco complesse accanto a forme molto complesse testimonia non la sostituzione di sistemi meno complessi con sistemi più complessi, ma la coesistenza di sistemi a vario grado di complessità. Inoltre è anche noto che nel corso dell'evoluzione vi sono stati non pochi casi in cui i sistemi viventi sono andati incontro a processi di drastica semplificazione di alcune subunità, dunque a una riduzione della loro c. generale. È il caso, assai popolare, della semplificazione anatomica dell'occhio, fino alla sua scomparsa totale e definitiva negli animali ciechi e anoftalmi che vivono negli ambienti cavernicoli. Un'evoluzione regressiva analoga è presentata dai parassiti intestinali nei quali si assiste, tra l'altro, alla perdita dell'apparato digerente.

Informazione e complessità

Nei sistemi viventi l'informazione è conservata e trattata negli acidi nucleici che specificano in maniera non lineare i vari fenotipi; i quali, a loro volta, manifestano c. gerarchizzata. Nel decennio successivo al 1953, dopo che J. Watson e F. Crick ebbero scoperto la struttura a doppia elica del DNA, alcuni ricercatori formularono in maniera rigorosa il problema dell'esistenza di un 'codice genetico' (l'insieme delle regole con cui una sequenza di nucleotidi di un gene viene tradotta nella sequenza di amminoacidi di una proteina). La prossimità temporale tra la scoperta dell'esistenza di un tale codice e l'elaborazione teorica della nozione di informazione, sviluppata nel contesto di problemi tecnologici di ingegneria delle comunicazioni a opera di C.E. Shannon e W. Weaver nel 1949, concorsero a suggerire l'accostamento tra l'informazione biologica e l'informazione quale è intesa nella teoria omonima. Precisamente, vennero cercate correlazioni e analogie sulla misura del contenuto di informazione di sequenze (normali e mutanti per una o più variazioni) e sulla misura dell'entropia di informazione.

In questo approccio, le sequenze nucleotidiche vengono considerate sequenze di simboli dell'alfabeto a quattro lettere proprie degli acidi nucleici. La formazione di una data sequenza Ik di lunghezza n avviene allora con probabilità pk=4⁻ⁿ, e il contenuto di informazione, espresso in bit, della sequenza è Ik=2n , indipendentemente dalla particolare sequenza considerata. In effetti l'informazione di Shannon considera solo la componente statistica dell'informazione senza riferimento al suo contenuto, dunque al significato, che è invece estremamente importante per i sistemi viventi, dato che è il significato del messaggio a determinare le conseguenze dell'informazione erogata. Approcci successivi dovuti a A.N. Kolmogorov e G.J. Chaitin considerarono la struttura interna delle sequenze. Nella teoria algoritmica dell'informazione il contenuto informativo di un messaggio è pari alla lunghezza del più piccolo programma di computer che, una volta eseguito, è in grado di produrre l'oggetto. Ne deriva che messaggi periodici o molto ridondanti possiedono basso rapporto di informazione algoritmica/c., mentre sequenze casuali hanno un alto rapporto di informazione algoritmica/c., non potendo essere create attraverso un programma che sia più breve delle sequenze stesse. Tuttavia il fatto che una sequenza casuale sia dotata di alta c. contraddice la realtà biologica, nella quale i sistemi altamente complessi non hanno strutture e comportamenti governati dal caso, ma sono invece altamente organizzati al loro interno. Anche se la nozione di c. algoritmica, essendo interessata alla struttura interna del messaggio, risponde meglio alle esigenze dei biologi, tuttavia non consente di affrontare il problema cruciale del significato. Quanto sia importante questo punto è chiaro considerando per es. che i geni strutturali dell'uomo e dello scimpanzé sono identici al 99% e che basta solo una frazione piccola, ma altamente significativa, di geni diversi per determinare differenze biologiche di grande rilievo. Le differenze di sequenza nel DNA tra uomo e scimpanzé consistono prevalentemente di differenze nell'uso del codice per quanto riguarda le sequenze tradotte e di variazioni nelle sequenze non trascritte. La distanza genetica media tra le due specie, stimata su circa cinquanta geni strutturali, è risultata essere addirittura inferiore a quella tra specie sorelle, che sono per definizione anatomicamente poco distinguibili. Tali piccole differenze, capaci però di generare differenze organizzative tra le due specie, vanno quasi certamente ricondotte a cambiamenti a carico di pochi geni regolatori.

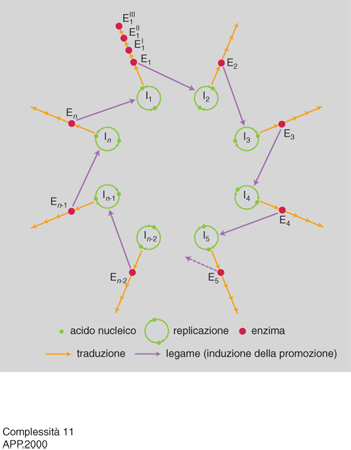
Il passaggio critico nella gerarchia della c. corrisponde ovviamente all'incremento di c. dei sistemi viventi, particolarmente intenso durante le transizioni evolutive più importanti (per es. il passaggio da cellula procariotica a cellula eucariotica, da sistema unicellulare a sistema pluricellulare, da individuo a colonia). Pur in mancanza di una teoria generale dell'incremento di c., questo fenomeno ha iniziato ad avere una sua spiegazione circoscrivendo l'analisi a sistemi molto semplici come i virus. A cavallo tra la fine degli anni Settanta e i primi anni Ottanta M. Eigen e P. Schuster hanno proposto un modello teorico, detto dell'iperciclo, di notevole interesse euristico, in cui sono specificate le condizioni minime che permettono di conservare e accumulare informazione biologica: un passo indispensabile per l'aumento di c. di un sistema.

11

12

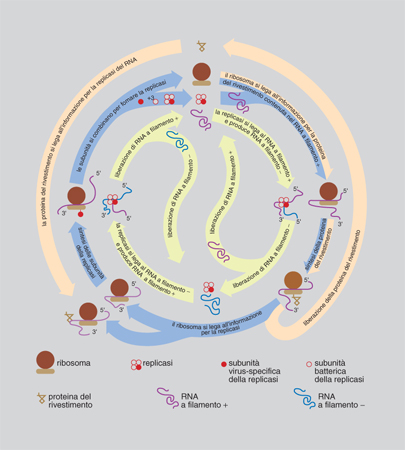
L'iperciclo di Eigen e Schuster è un concatenamento chiuso di cicli di reazioni in cui enzimi e acidi nucleici promuovono reciprocamente le loro sintesi (fig. 11 e 12). Dato che le molecole replicanti sono dipendenti le une dalle altre (c'è cooperazione), cambia la dinamica di popolazione e gli individui molecolari non competono (come invece accade con la replicazione indipendente delle molecole, che provoca competizione e produzione di 'quasispecie': una distribuzione di individui mutanti centrata su una o più sequenze dominanti, analoga al tipo selvatico della genetica classica) ma si integrano a un livello più elevato. Nel modello dell'iperciclo la transizione al gradino superiore avviene in più fasi: i replicatori indipendenti competono per le risorse e ottimizzano la propria fitness individuale; l'interdipendenza riproduttiva riduce, fino a eliminarla, la competizione tra replicatori; la riproduzione fra replicatori cooperanti ha come effetto la formazione di un'unità funzionale dove sono integrate le diverse funzioni di fenotipi differenti; la compartimentalizzazione dei replicatori crea, attraverso l'integrazione spaziale, una nuova unità di selezione; l'integrazione dei replicatori produce una nuova classe di individui replicatori passibili di evoluzione autonoma: i genotipi dei replicatori inizialmente autonomi formano un genoma unico, più grande. Tra l'altro, il modello prevede l'interazione con individui molecolari 'parassiti', che traggono vantaggio temporaneo dalla nuova organizzazione senza integrarvisi, e individua nell'abbondanza di risorse la condizione più favorevole all'integrazione.

L'incremento della c. di un sistema può avvenire anche per altre vie. La duplicazione genica e genomica, per es., è un meccanismo che consente ai geni duplicati di sviluppare eventuali nuove funzioni. In condizioni ambientali favorevoli (risorse abbondanti e di basso costo energetico) le varianti nuove con genoma accresciuto competono con successo contro le varianti più piccole ma ottimizzate.

Le condizioni da soddisfare perché vi sia incremento di informazione e di c. nell'evoluzione riguardano la componente relazionale della c. e sono: l'esistenza di un meccanismo per la 'simbiosi' (come nel caso della produzione della cellula eucariote, che sotto questo aspetto può essere vista come una cellula 'pluricellulare') e l'esistenza di un meccanismo per l'epigenesi.

Selezione naturale. - In larga misura la storia dei sistemi viventi è storia dei passaggi da un livello di c. all'altro, ovvero, analogamente secondo molti ricercatori, da un'unità di selezione all'altra. L'avvio del processo evolutivo ha coinciso con l'originarsi di molecole capaci di autoreplica; queste vengono poi incorporate in unità cellulari assai ben delimitate, capaci successivamente di integrare al loro interno i genomi di organelli dotati di autoreplicabilità, e poi in grado di sfruttare (come popolazioni non come individui), grazie alla sessualità, l'enorme vantaggio della ricombinazione genetica, con l'incorporazione e la rapida diffusione delle combinazioni più vantaggiose. A questo punto del processo evolutivo, con la comparsa del sesso e delle specie, la selezione naturale assume la forma, che è più familiare ai biologi, di riproduzione differenziale di genotipi.

Il modello esplicativo elaborato con la 'teoria sintetica dell'evoluzione' è appunto centrato sulla riproduzione differenziale di varianti individuali all'interno di una variazione intrapopolazionale di caratteri ereditabili. Tuttavia, è opinione diffusa che questo modello esplicativo vada ora modificato per accogliere le moderne acquisizioni della biologia a livello molecolare, cellulare e dello sviluppo. I dati sperimentali portati da queste discipline hanno cominciato a chiarire, individuandone in molti casi i meccanismi, le fasi del processo di incremento di c. precedente la comparsa del livello di popolazione-specie. Sebbene tutte queste conoscenze mancassero all'epoca della formulazione della teoria sintetica (1936-47), e siano continuate a mancare ancora per alcuni decenni, molti biologi sulla base di risultati di ricerche condotte con metodi tradizionali avevano sollevato già negli anni Sessanta (venti, trent'anni dopo i primi pronunciamenti di autori come J.B.S. Haldane, S. Wright, W.C. Allee ecc.) la questione della probabile esistenza di livelli di azione multipli della selezione naturale, sia al di sopra sia al di sotto del livello individuale.

Il quadro generale che sta dietro all'idea della molteplicità delle unità di selezione è che al nascere di un nuovo livello organizzativo si verifica un cambiamento nel bersaglio e nella forma della selezione. In un primo momento la selezione viene esercitata soltanto dall'ambiente esterno; con la nascita del nuovo livello strutturale (se esso contiene fisicamente il livello strutturale più antico), l'ambiente esterno agisce direttamente solo sull'unità di questo nuovo livello: la selezione sull'unità gerarchicamente inferiore non è più esercitata dallo stesso ambiente di prima (quello che precedentemente era esterno) ma dall'unità neoformata, che pertanto funzionerà come ambiente per l'unità più vecchia e gerarchicamente inferiore. Questa concezione prevede un controllo verticale, dall'alto, dell'unità maggiore sull'ambito delle possibili variazioni dell'unità minore. E anche se, in effetti, i cambiamenti dell'unità di livello inferiore possono arrivare a influenzare la replica dell'unità del livello immediatamente superiore, tale azione dal basso è consentita nella misura in cui questi cambiamenti non sono svantaggiosi per l'unità maggiore che interagisce con l'ambiente esterno. In questa visione, all'incremento di c. è associato lo slittamento della selezione dal vecchio al nuovo livello di organizzazione, che quindi perde gradi di libertà trasformandosi in vincolo interno al sistema.

Un esempio convincente di incremento della c. biologica strutturale con importanti effetti di regolazione funzionale è offerto dal fenomeno del linkage disequilibrium (disequilibrio da associazione). Si è constatato che geni strettamente associati sul cromosoma tendono a trovarsi in uno stato di disequilibrio da associazione. In questo caso l'organizzazione del cromosoma riduce la probabilità che, dentro i gameti, alleli di siti variabili si trovino associati a caso: tale organizzazione rappresenta un vincolo per questo fenomeno. Questo controllo può essere esercitato dall'alto come risultato di una storia evolutiva con una forte componente deterministica: è il caso delle inversioni paracentriche polimorfiche del terzo cromosoma di Drosophila pseudoobscura. Tali inversioni cromosomiche, ben note ai genetisti, opponendosi ai normali meccanismi di ricombinazione, rappresentano una forma di organizzazione spaziale del cromosoma, selettivamente premiata, nella quale si trovano riuniti alleli che di per sé possono non fornire elevatissimi vantaggi, ma che nella forma associata interagiscono tra loro conferendo un vantaggio selettivo all'individuo portatore. L'inversione paracentrica conferisce vantaggio al gruppo perché, riducendo la frequenza dei genomi ricombinanti, protegge gli assortimenti aploidi vantaggiosi. Il fatto che qui interessa è che, se l'inversione fornisce un vantaggio selettivo al suo portatore, non è necessario che la selezione su ogni singolo locus genico sia forte (con bassa ricombinazione, infatti, il coefficiente di accoppiamento tra geni può essere molto grande, senza che vi siano grosse differenze negli effetti medi degli alleli ai loci separati, detti fitness marginali).

Fenomeni come quello descritto dimostrano che i singoli geni non evolvono indipendentemente. Da qui, ancora una volta, l'impossibilità di prevedere la dinamica evolutiva di singoli geni se questi sono organizzati in un'unità evolutiva di ordine superiore. Nel caso del coadattamento genetico, quindi, l'unità di selezione non coincide con singoli geni ma con più ampie frazioni di genoma. Più in generale nei sistemi viventi l'unità di selezione dovrebbe essere identificabile, almeno in linea di principio, a diversi livelli purché essa si replichi e conservi la propria identità col passare delle generazioni.

Complessità biologica e storia

Uno degli aspetti più ricchi di conseguenze, sebbene immediatamente non appariscente, dei sistemi viventi è quello di essere sistemi non universalmente necessitati, nel senso che le loro strutture e i loro comportamenti non sono descrivibili con leggi universali, bensì con enunciati validi caso per caso, o tutt'al più validi per una casistica assai limitata. Da cosa derivi questa caratteristica è facilmente comprensibile, considerando i seguenti esempi quantitativi che illustrano un peculiare aspetto dei sistemi viventi: l'enorme discrepanza tra quanto è teoricamente possibile su base combinatoria e quanto invece si è storicamente realizzato.

Diversità molecolare. - Una proteina di piccolo peso molecolare è costituita da circa 300 amminoacidi, ognuno dei quali è codificato da tre nucleotidi; perciò i geni che specificano la proteina sono costituiti da circa 1000 nucleotidi. All'interno di ciascuna catena, ogni nucleotide rappresenta una sola tra quattro possibilità. Il numero di tutte le possibili catene è allora eguale a 4¹⁰⁰⁰, ovvero circa 10⁶⁰⁰. Il numero di sequenze amminoacidiche immaginabili è quindi 10⁶⁰⁰, ma solo una frazione piccolissima possiede la stabilità e l'attività enzimatica necessarie a garantire il funzionamento cellulare. La probabilità che l'ottimalità di queste sequenze amminoacidiche sia nata per caso è praticamente zero ed è necessario ipotizzare l'esistenza di una causa, di un fattore deterministico sotto forma di selezione. Inoltre, considerando anche che la vita sul pianeta ha meno di 4 miliardi di anni, un lasso di tempo breve rispetto alla potenziale produzione di combinazioni di amminoacidi, si deve concludere che deve esservi stata un'azione selettiva particolarmente intensa.

Polimorfismo. - Partendo da 6000 geni strutturali (numero medio stimato per Drosophila) e ammettendo verosimilmente che la metà sia polimorfica, avremo 3000 geni. Assumendo una media di 2 alleli per locus elettroforetico, avremo 3 possibili combinazioni alleliche per locus, che per tutti i loci dà un numero totale di combinazioni alleliche pari a 3³⁰⁰⁰ (6³⁰⁰⁰ nel caso diploide). Questa è una cifra strabiliante, non solo assolutamente superiore al totale dei genotipi aploidi già prodotti e producibili in futuro, ma anche di gran lunga superiore al numero stimato di tutte le particelle elementari del nucleo atomico (protoni, elettroni ecc.) presenti nell'universo (circa 10⁷⁹). La massa di questi genotipi supererebbe, se tutti fossero prodotti, la massa dei nucleoni.

Il fatto, invece, che di tutte le possibili combinazioni genotipiche solo alcune effettivamente si siano realizzate, e solo alcune altre si realizzeranno, rappresenta una chiara evidenza della natura relativa e contingente dei sistemi biologici. È questa contingenza a fondare la natura storica dei viventi: la c. osservabile deriva da vincoli strutturali e funzionali preesistenti, che a loro volta determinano la dinamica futura dei sistemi. Non tutti i cammini evolutivi sono dunque possibili ma solo quelli compatibili con il regime di vincoli esterni e interni al sistema. I sistemi viventi sono dunque entità storicamente determinate e la biologia assume anch'essa carattere storico ogni volta che si pone problemi che vanno oltre il comportamento delle molecole.

Ci si potrebbe chiedere infine se sia opportuna un'indagine 'al di là delle molecole' e dei loro comportamenti. La risposta è affermativa perché la natura dei vincoli che determinano le condizioni di possibilità dei sistemi viventi è esplicitabile solo in termini evolutivi. La ricerca ha iniziato a fare luce sulla natura di questi vincoli. Si tratta dei vincoli adattativi, sincronici, che strutturano il collegamento con i fattori ambientali, e dei vincoli di sviluppo che specificano diacronicamente il modo d'essere di ciascun individuo e di ciascuna specie. La natura di questi vincoli legittima, inoltre, gli interrogativi teleonomici sui perché di certe manifestazioni dei viventi. Il nucleo delle risposte alle domande sui perché non è niente altro che la descrizione della comparsa e dell'affermazione nel tempo dei vincoli capaci di conferire identità agli organismi, oppure di trasformarla. Le domande sui perché non sembrano riducibili a domande sul come. Piuttosto si hanno spiegazioni di due ordini distinti: una funzionale, finalizzata all'esplicitazione delle cause prossime, dei meccanismi in gioco; l'altra tesa a elaborare una spiegazione che è storia delle vicende responsabili del fenomeno indagato. Sul piano della generalizzazione, questa storia funziona come modello esemplare, esplicativo per tutta la serie di eventi assimilabili a quello studiato.

bibliografia

M. Eigen, P. Schuster, The hypercycle. A principle of natural self-organization, Berlin-New York 1979 (trad. it. Iperciclo, Rovigo 1982).

M. Ageno, Le radici della biologia, Milano 1986.

L.W. Buss, The evolution of individuality, Princeton (N.J.) 1987.

J.T. Bonner, The evolution of complexity by means of natural selection, Princeton (N.J.) 1988.

P.W. Signor, The geologic history of diversity, in Annual review of ecology and systematics, 1990, 21, pp. 509-39.

Biodiversity and ecosystem function, ed. E.-D. Schulze, H.A. Mooney, Berlin-New York 1993.

V.H. Heywood, R.T. Watson, Global biodiversity assessment, Cambridge-New York 1995.

J. Maynard Smith, E. Szathmary, The major transitions in evolution, Oxford-New York 1995.

Defining life. The central problem in theoretical biology, a cura di M. Rizzotti, Padova 1996.

E. Mayr, This is biology. The science of the living world, Cambridge (Mass.) 1997 (trad. it. Il modello biologico, Milano 1998).

Il pensiero della complessità

di Edgar Morin

Ordine, separabilità e 'ragione assoluta' costituiscono i tre pilastri su cui si è edificato il pensiero scientifico classico. Ma oggi le loro basi sono in crisi, proprio in conseguenza dello sviluppo di quelle scienze che in origine si erano fondate su questi tre pilastri. L'emergere delle idee sulla c. rende necessario riformulare il nostro modo di pensare e costituisce una sfida importante per la filosofia contemporanea.

Il pensiero complesso inizia a svilupparsi nel punto di confluenza di due rivoluzioni scientifiche. La prima rivoluzione - con la termodinamica, la fisica quantistica e la cosmofisica - ha introdotto l'incertezza. Questa rivoluzione scientifica ha avviato le importanti riflessioni epistemologiche di K.R. Popper, T.S. Kuhn, G. Holton, I. Lakatoš, P.K. Feyerabend, i quali hanno dimostrato che la scienza non è certezza ma ipotesi, che una teoria provata non lo è mai in modo definitivo e che resta 'falsificabile', che la scientificità stessa contiene al proprio interno qualcosa di non-scientifico (postulati, paradigmi, themata). La seconda rivoluzione scientifica, più recente e ancora molto ricca di zone d'ombra, è la rivoluzione sistemica, la quale però non ha ancora molto trovato il suo prolungamento epistemologico, per quanto alcuni autori cerchino di muoversi in questa prospettiva.

La nozione di ordine nasceva da una concezione deterministica e meccanicistica del mondo. Ogni disordine apparente era considerato il frutto della nostra 'provvisoria' ignoranza. Dietro questo disordine apparente c'era un ordine nascosto che doveva essere scoperto. Questa idea di un ordine universale è stata messa in discussione innanzitutto dalla termodinamica, che ha riconosciuto nel calore un'agitazione molecolare disordinata, quindi dalla microfisica, dalla cosmofisica, e ai nostri giorni dalla fisica del caos. Le idee di ordine e di disordine hanno smesso di escludersi a vicenda in modo assoluto: per un verso un ordine organizzatore può nascere in condizioni che rasentano la turbolenza, per un altro verso processi disordinati possono nascere a partire da iniziali stati deterministici.

Il pensiero complesso, lungi dal sostituire l'idea di ordine con quella di disordine, mira a porre in rapporto dialogico l'ordine, il disordine e l'organizzazione.

Il secondo pilastro del pensiero classico è la nozione di separabilità. Essa corrisponde al principio cartesiano secondo cui, per studiare un fenomeno o risolvere un problema, è necessario scomporli in elementi semplici. In campo scientifico questo principio si è tradotto per un verso nella specializzazione e, quindi, nella iperspecializzazione disciplinare, per un altro verso nell'idea che la realtà oggettiva possa essere considerata indipendentemente dall'osservatore. Nell'ultimo quarto del 20° sec., si sono sviluppate alcune 'scienze sistemiche' che concatenano ciò che le discipline tradizionali separano, e che hanno come oggetto le interazioni tra elementi e non più la loro separazione. L'ecologia in quanto scienza ha come oggetto gli ecosistemi e la biosfera, insiemi di costituenti interdipendenti che, isolati, rientrano nel campo della zoologia, della botanica, della microbiologia, della geografia, delle scienze fisiche e così via (v. sopra). Le scienze della Terra concepiscono il nostro pianeta come un sistema complesso che si autoproduce e si autoorganizza; esse articolano tra loro discipline - un tempo separate - come la geologia, la meteorologia, la vulcanologia, la sismologia. Un altro aspetto della separabilità - quello della disgiunzione tra l'osservatore e ciò che viene osservato - è ugualmente stato messo in discussione dalla fisica contemporanea. In microfisica, da W. Heisenberg in poi, sappiamo che l'osservatore interferisce con l'oggetto della sua osservazione. Nelle scienze umane e sociali, è ormai sempre più evidente che nessun sociologo o nessun economista potrebbe troneggiare - come la stella Sirio - al di sopra della società. Ciascuno costituisce un frammento di questa società, e la società, in quanto tutto, è al suo interno.

Il pensiero complesso non sostituisce l'inseparabilità alla separabilità, esso fa appello a una modalità dialogica che utilizza il separabile inserendolo nell'inseparabile.

Il terzo pilastro del nostro modo di pensare è rappresentato dalla logica induttiva-deduttiva-identitaria che si identifica in una 'ragione assoluta'. La 'ragione classica' poggiava sui tre principi di induzione, deduzione e identità (sul rifiuto cioè della contraddizione). Da Popper è stata mossa la prima critica violenta all'induzione, con la quale si presumeva di trarre leggi generali da esempi particolari. Popper ha giustamente fatto notare che, a rigor di termini, non era possibile inferire un'affermazione universale come "Tutti i cigni sono bianchi" dal semplice fatto di non averne mai visti di neri. L'induzione ha incontestabilmente un valore euristico, ma non ha valore di prova assoluta.

Il teorema di incompletezza di K. Gödel mostra, d'altronde, che un sistema deduttivo formalizzato non può trovare in se stesso la dimostrazione assoluta della propria validità. È quanto è stato mostrato anche da A. Tarski nella sua logica semantica: nessun sistema dispone di mezzi sufficienti per autodimostrare se stesso. È possibile, talvolta, trovare prove o spiegazioni in alcuni metasistemi, ma anche questi ultimi presentano comunque dei limiti. Indubbiamente si possono elaborare dei 'meta-punti di vista': per es., per conoscere la società in cui vivo posso comparare tra loro le società contemporanee, studiare per contrasto le società antiche, o anche immaginare società 'possibili'. Ciò mi consente di costruire una sorta di osservatorio a partire dal quale posso osservare altre società esterne pur continuando a rimanere all'interno della mia. Ma in ogni caso non esiste un metasistema teorico in grado di farci andare oltre la nostra condizione sociale o la nostra condizione umana, di trasformarci cioè in esseri metasociali o metaumani. Infine, le acquisizioni di alcune scienze, come la microfisica o la cosmofisica, sono pervenute in modo empirico-razionale a contraddizioni insormontabili, come quella che riguarda l'apparente doppia natura contraddittoria della particella (onda-corpuscolo), o quelle che concernono l'origine dell'universo, della materia, del tempo, dello spazio.

Così, se non si può fare a meno della logica induttiva-deduttiva-identitaria, essa non può costituire lo strumento della certezza e della prova assoluta. Il pensiero complesso non comporta l'abbandono di questa logica, bensì una combinazione dialogica tra la sua utilizzazione, segmento per segmento, e la sua trasgressione nei buchi neri in cui essa cessa di essere operativa.

Le tre teorie

Ordine, separabilità e ragione assoluta - i tre pilastri del nostro modo di pensare - sono stati dunque profondamente scossi dagli sviluppi delle scienze contemporanee. Ciò dato, come è possibile inoltrarsi in un universo in cui l'ordine non è più assoluto, in cui la separabilità è limitata e in cui la logica stessa appare vacillare? È questo il problema fondamentale che il pensiero della c. vuole affrontare. Una prima via di accesso è quella che possiamo definire delle 'tre teorie': la teoria dell'informazione, la cibernetica e la teoria dei sistemi. Queste tre teorie, strettamente connesse e inseparabili, hanno fatto la loro comparsa all'inizio degli anni Quaranta e si sono ampiamente fecondate a vicenda.

La teoria dell'informazione è uno strumento con cui è possibile trattare l'incertezza, la sorpresa e l'imprevisto (v. informazione, teoria della, App. III, ed entropia: Entropia e informazione, App. V). Così l'informazione che indica chi è il vincitore di una battaglia risolve un'incertezza, e quella che annuncia la morte improvvisa di un tiranno introduce l'imprevisto oltre che la novità. Questo concetto di informazione permette di accedere a un universo in cui esistono sia l'ordine (la ridondanza) sia il disordine (il rumore), e di estrarne il nuovo (l'informazione). Inoltre, l'informazione può assumere forma organizzatrice (programmatrice) all'interno di una macchina cibernetica. L'informazione diventa allora ciò che controlla l'energia e ciò che dà autonomia a una macchina.

La cibernetica è in se stessa una teoria delle macchine autonome (v. cibernetica, App. III e IV). L'idea di retroazione, introdotta da N. Wiener (1950), rompe col principio di causalità lineare introducendo l'idea di causalità circolare. A agisce su B e B agisce a sua volta su A. La causa agisce sull'effetto e l'effetto sulla causa, come in un sistema di riscaldamento in cui il termostato regola il funzionamento della caldaia. Questo meccanismo, detto di regolazione, è ciò che permette l'autonomia di un sistema, in questo caso l'autonomia termica di un appartamento rispetto al freddo esterno. Come W.B. Cannon ha mostrato molto bene in The wisdom of the body (1932), nel caso di un organismo vivente l'omeostasi è un insieme di processi di regolazione fondati su molteplici retroazioni. Il circuito di retroazione (chiamato feedback) permette - nella sua forma negativa - di stabilizzare un sistema, di ridurre la devianza, come accade appunto nel caso dell'omeostasi. Nella sua forma positiva il feedback è un meccanismo di amplificazione, come per es. nella situazione di estremizzazione di un conflitto armato. La violenza di un protagonista comporta una reazione violenta che, a sua volta, comporta una reazione ancora più violenta. Simili retroazioni, di tipo inflazionistico o stabilizzatore, sono miriadi nei fenomeni economici, sociali, politici o psicologici. L'idea di retroazione era stata intuita da K. Marx quando affermava che l'infrastruttura materiale di una società produce la sovrastruttura (sociale, politica, ideologica), ma che, a sua volta, la sovrastruttura retroagisce sull'infrastruttura materiale.

Anche la teoria dei sistemi pone le basi per un pensiero dell'organizzazione. Il concetto di base di questa teoria è che "il tutto è più della somma delle parti". Ciò significa che esistono qualità emergenti che nascono dall'organizzazione di un tutto e che possono retroagire sulle parti. Così l'acqua ha qualità emergenti rispetto all'idrogeno e all'ossigeno che la compongono. E si potrebbe aggiungere anche che il tutto è meno della somma delle parti, visto che le parti possono avere qualità che sono inibite dall'organizzazione dell'insieme. La teoria dei sistemi ci aiuta anche a pensare le gerarchie dei livelli di organizzazione, i sottosistemi e le loro embricazioni.

L'insieme di queste tre teorie - teoria dell'informazione, cibernetica e teoria dei sistemi - ci introduce in un universo di fenomeni organizzati in cui l'organizzazione avviene con e contro il disordine.

L'autoorganizzazione

A queste tre teorie bisogna aggiungere gli sviluppi concettuali introdotti dall'idea di autoorganizzazione. A questo proposito vanno ricordati i nomi di J. von Neumann, H. von Foerster, H. Atlan e I. Prigogine. Nella sua teoria degli automi auto-organizzatori von Neumann si è posto il problema della differenza tra macchine artificiali e 'macchine viventi'. Egli ha messo in evidenza questo paradosso: gli elementi delle macchine artificiali sono di ottima fattura, molto perfezionati, ma cominciano a degradarsi nel momento stesso in cui la macchina inizia a funzionare. Le macchine viventi, al contrario, sono composte da elementi scarsamente affidabili - come le proteine, che si degradano di continuo - ma queste macchine possiedono singolari proprietà di svilupparsi, di riprodursi, e di autorigenerarsi, rimpiazzando le molecole degradate con nuove molecole e le cellule morte con nuove cellule. La macchina artificiale non è in grado di ripararsi da sola, di autoorganizzarsi e di svilupparsi, mentre la macchina vivente si rigenera in permanenza via via che le sue cellule muoiono.

Il contributo di von Foerster consiste nella scoperta del principio dell'ordine dal rumore (order from noise). Così, dei cubi magnetizzati su due facce organizzano un insieme coerente per assemblaggio spontaneo sotto l'effetto di un'energia non direzionale, a partire da un principio d'ordine (la magnetizzazione). Si assiste dunque alla creazione di un ordine a partire dal disordine. A questo punto Atlan (1979) ha potuto concepire la sua teoria del 'caso organizzatore'. Una relazione dialogica ordine/disordine/organizzazione è presente al momento della nascita dell'universo a partire da un'agitazione calorifica (disordine), quando in determinate condizioni (incontri casuali) alcuni principi d'ordine favoriscono la costituzione dei nuclei, degli atomi, delle galassie e delle stelle. Questa stessa relazione dialogica è presente anche nel momento in cui la vita emerge a seguito dell'incontro tra macromolecole all'interno di una sorta di circuito autoproduttore che finirà per diventare autoorganizzazione vivente. Sotto le più svariate forme, la relazione dialogica tra l'ordine, il disordine e l'organizzazione - tramite innumerevoli inter-retroazioni - agisce di continuo nel mondo fisico, in quello biologico e in quello umano.

Prigogine, con la sua termodinamica dei processi irreversibili, ha introdotto in altri termini l'idea di organizzazione a partire dal disordine. Nell'esempio dei vortici di H. Benard possiamo vedere come strutture coerenti si costituiscano e si autoalimentino, a partire da una certa soglia di agitazione e al di qua di un'altra soglia, in condizioni di crescente disordine. Beninteso, queste organizzazioni hanno bisogno di essere alimentate tramite energia, e di consumare, 'dissipare', energia per mantenersi. Nel caso dell'essere vivente, esso è abbastanza autonomo da poter attingere energia nel suo stesso ambiente e anche da poterne ricavare informazioni e da integrarne l'organizzazione. È ciò che può essere chiamato l'auto-eco-organizzazione.

Il pensiero della c. si presenta dunque come un edificio a più piani. La base è costituita dalle tre teorie dell'informazione, della cibernetica e dei sistemi, e contiene gli strumenti necessari per una teoria dell'organizzazione. Segue un secondo piano in cui troviamo le idee di von Neumann, von Foerster e Prigogine sull'autoorganizzazione. A questo edificio si possono aggiungere alcuni elementi supplementari, e cioè il principio dialogico, il principio di recursione e il principio ologrammatico (Morin 1990).

Il principio dialogico unisce due principi o nozioni antagonistiche, che apparentemente dovrebbero respingersi a vicenda, ma che sono indissociabili e indispensabili per comprendere una stessa realtà. Il fisico N. Bohr, ha per esempio, riconosciuto la necessità di pensare le particelle della fisica sia come corpuscoli sia come onde. Come dice B. Pascal: "Il contrario di una verità non è l'errore, ma una verità contraria". Bohr rielabora questo concetto a suo modo: "Il contrario di una verità banale è un errore stupido, ma il contrario di una verità profonda è sempre un'altra verità profonda". Il problema fondamentale è dunque quello di unire nozioni antagonistiche per pensare i processi di organizzazione, produzione e creazione nel mondo complesso della vita e della storia umana.

Il principio di recursione organizzatrice va al di là del principio di retroazione (feedback); esso va oltre la nozione di regolazione per introdurre quella di autoproduzione e di autoorganizzazione. Si tratta di un circuito generatore in cui i prodotti e gli effetti sono essi stessi produttori e causa di ciò che li produce. Così, ogni individuo è il prodotto di un sistema di riproduzione che risale a tempi antichissimi, ma questo sistema può riprodursi solo se gli individui ne divengono i produttori accoppiandosi. Gli esseri umani producono la società 'nelle' e 'attraverso' le interazioni, ma la società, in quanto tutto emergente, produce l'umanità di questi individui fornendo loro il linguaggio e la cultura.

Il principio ologrammatico, il terzo principio, mette infine in evidenza l'apparente paradosso di alcuni sistemi in cui non soltanto la parte è nel tutto, ma il tutto è nella parte. Così, ogni cellula è una parte di un tutto - l'organismo globale - ma il tutto è esso stesso nella parte: la totalità del patrimonio genetico è presente in ogni cellula individuale. Analogamente, l'individuo è una parte della società, ma la stessa società è presente, nella sua globalità, in ogni individuo, attraverso il linguaggio, la cultura, le norme ecc.

Come si può vedere, il pensiero della c. propone un certo numero di strumenti concettuali che derivano dalle tre teorie e dalle concezioni dell'autoorganizzazione, ma esso sviluppa anche strumenti propri. Non è affatto un pensiero che respinge la certezza per introdurre l'incertezza, né respinge la separazione per sostituirla con l'inseparabilità, né ripudia la logica per rendere legittime tutte le trasgressioni: il procedimento consiste, al contrario, nell'operare un continuo andirivieni tra certezze e incertezze, tra elementare e globale, tra separabile e inseparabile. Nello stesso tempo, si continua a utilizzare la logica classica così come i principi di identità, di non-contraddizione, di deduzione e di induzione, ma si è consapevoli dei loro limiti e in alcuni casi è possibile, anzi è necessario, trasgredirli. Non si tratta dunque di abbandonare i principi della scienza classica - ordine, separabilità e logica - ma di integrarli in uno schema che è nello stesso tempo più ampio e più ricco. Non si tratta di opporre un olismo globale imperfetto a un riduzionismo sistematico; si tratta piuttosto di connettere il concreto delle parti alla totalità. È necessario articolare i principi di ordine e di disordine, di separazione e di unificazione, di autonomia e di dipendenza, i quali sono in relazione dialogica (complementari, concorrenti e antagonistici) in seno all'universo. Insomma, il pensiero complesso non è il contrario del pensiero semplificante, ma una sua integrazione; esso opera l'unione della semplicità e della c., e inoltre, nel metasistema a cui dà origine, rende evidente la sua semplicità. Il paradigma della c. può essere enunciato in modo altrettanto semplice di quello di semplificazione: quest'ultimo impone di disgiungere e di ridurre; il paradigma della c. ingiunge di collegare pur distinguendo.

Il pensiero complesso è, in sostanza, il pensiero che prende in considerazione l'incertezza e che è capace di concepire l'organizzazione. È il pensiero capace di collegare (complexus), di contestualizzare, di globalizzare; ma è capace nello stesso tempo di riconoscere il singolare, l'individuale, il concreto.

bibliografia

A.N. Whitehead, Science and the modern world, Cambridge (Mass.) 1926 (trad. it. Torino 1979).

K. Gödel, Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme, in Monatshefte für Mathematick und Physik, 1931, pp. 173-198.

A.E. Schrödinger, What is life?, Cambridge-New York 1945.

A. Rosenblueth, N. Wiener, Purposeful and non purposeful behavior, in Philosophy of science, 1950, 17, pp. 318-26.

N. Wiener, The human use of human beings: cybernetics and society, Boston (Mass.) 1950.

L. Brillouin, Science and information theory, New York 1956.

N.H.D. Bohr, Atomfysik og menneskelig erkendelse, København 1957 (trad. it. sull'ed. ingl. 1958, Teoria dell'atomo e conoscenza umana, Torino 1961).

J. Ladrière, Les limitations internes des formalismes. Étude sur la signification du théorème de Gödel et des théorèmes apparentés dans la théorie des fondements des mathématiques, Louvain-Paris 1957.

Th.S. Kuhn, The structure of scientific revolutions, Chicago (Ill.) 1962 (trad. it. Torino 1969).

Principles of self-organization, ed. H. von Foerster, G.W. Zopf, New York 1962.

M. Maruyama, The second-cybernetics: deviation amplifying mutual causal processes, in American scientist, 1963, 51, pp. 164-79, 250-56.

J. von Neumann, Theory of self-reproducing automata, Urbana (Ill.) 1966.

J.B. Grize, Logique et connaissance scientifique, Paris 1967.

Logique et connaissance scientifique, sous la direction de J. Piaget, Paris 1967 (Encyclopédie de la Pléiade, 22).

G. Bachelard, Le nouvel esprit scientifique, Paris 1968 (trad. it. Roma-Bari 1978).

L. von Bertalanffy, General systems theory. Foundations, development, applications, New York 1968 (trad. it. Milano 1971).

G. Spencer-Brown, Laws of form, London 1969.

C. Castoriadis, Le monde morcelé, in Encyclopaedia universalis, vol. 17°, 1971, pp. 43-73.

G. Spencer-Brown, Only two can play this game, ed. J. Keys, New York 1972.

J. Ladrière, Système, in Encyclopaedia universalis, Paris 1973, ad vocem.

E. Morin, Le paradigme perdu. La nature humaine, Paris 1973, 1979² (trad. it. Milano 1974).

R. Chauvin, Les sociétés les plus complexes chez les insectes, in Communication, 1974, 22, pp. 63-72.

M. Maruyama, Paradigmatology and its application to cross-disciplinary, cross-professional and cross-cultural communication, in Cybernetica, 1974, 17, pp. 136-56, 237-81.

G.J. Chaitin, Randomness and mathematical proof, in Scientific American, 1975, 5, pp. 47-52.

J.-L. Le Moigne, La théorie du système général. Théorie de la modélisation, Paris 1977, ed. rivista e ampliata 1994⁴.

E. Morin, La méthode, Paris 1977-93 (trad. it. Milano 1983-1991, 4 voll.).

H. von Foerster, Selected papers, Amsterdam 1978.

H. Atlan, Entre le cristal et la fumée. Essai sur l'organisation du vivant, Paris 1979 (trad. it. Firenze 1987).

D.R. Hofstadter, Gödel, Escher, Bach. An eternal golden braid, New York 1979 (trad. it. Milano 1984).

I. Prigogine, I. Stengers, La nouvelle alliance. Métamorphoses de la science, Paris 1979 (trad. it. Milano 1979).

H.von Foerster, Observing systems, Seaside (Calif.) 1982 (trad. it. Roma 1987).

E. Morin, Science avec conscience, Paris 1982, 1990² (trad. it. Milano 1984).ù

E. Morin, Sociologie, Paris 1984, 1994².

La sfida della complessità, a cura di M. Ceruti, G. Bocchi, Milano 1985.

M. Ceruti, Il vincolo e la possibilità, Milano 1986.

E. Morin, Introduction à la pensée complexe, Paris 1990 (trad. it. Milano 1993).

J.-L. Le Moigne, Les épistémologies constructivistes, Paris 1995.