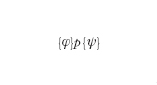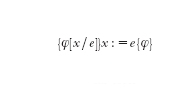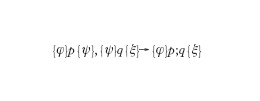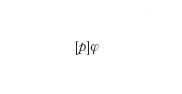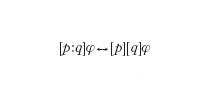Informatica
Informatica
(App. IV, ii, p. 189; V, ii, p. 704)
Mentre negli anni 1937-38 venivano pubblicati l'ultimo volume della Enciclopedia Italiana e l'App. I, alcuni ricercatori (K. Zuse in Germania, G. Stibitz e H.H. Aiken negli Stati Uniti) lavoravano intensamente alla progettazione di macchine calcolatrici elettromeccaniche, in grado di soddisfare la crescente esigenza di potenza di calcolo e di elaborazione automatica dell'informazione numerica, che era registrata nei volumi dell'Enciclopedia (v. calcolatrici, macchine, VIII, p. 352 e App. I, p. 339; statistica: Macchine per contabilità e statistica, App. I, p. 1018). Nel periodo intorno alla Seconda guerra mondiale furono sviluppate le prime macchine calcolatrici elettroniche, nelle quali venivano applicate le tecnologie in uso in radiotecnica e in telefonia: il moderno sviluppo tecnologico veniva così incontro ad aspirazioni molto più antiche relative all'automatizzazione e alla creazione di esseri artificiali in grado di riprodurre le capacità umane, incluso il pensiero (v. automa, V, p. 554). Un ampio ventaglio di ricerche nell'ambito della logica matematica (dall'algebra di G. Boole al concetto teorico di algoritmo di A. Turing, alle idee sull'architettura delle macchine calcolatrici di J. von Neumann) e nel campo delle tecniche di trasmissione dei messaggi (i cui principi di base furono stabiliti da Cl. Shannon) costituiscono il substrato teorico che rese possibile il perfezionamento dei calcolatori elettronici. Questo periodo pionieristico è ben considerato nelle App. II e III, nelle voci calcolatrici, macchine (App. II, i, p. 482; III, i, p. 281), elettronica (App. III, i, p. 532) e informazione, teoria della (App. III, i, p. 874), oltre che nella voce cibernetica (App. III, i, p. 368), che riprende le riflessioni generali e interdisciplinari sul confronto fra i processi di comunicazione o trasmissione dell'informazione nell'animale e nella macchina, sollecitate dai recenti sviluppi tecnologici (v. nell'App. III: automazione, i, p. 178, controlli automatici, i, p. 430 e servosistema, ii, p. 705). Negli anni Quaranta e Cinquanta vengono quindi sviluppate le prime macchine dotate di programmi registrati, in grado di eseguire in modo automatico sequenze prefissate di istruzioni. Queste macchine sono dette elaboratori elettronici (in francese il nuovo termine è ordinateur; ma internazionalmente si preferisce usare il termine inglese per 'calcolatore', computer). Dalle prime applicazioni militari si passa, negli anni successivi, alle applicazioni industriali su vasta scala, con la creazione dei grandi sistemi informativi; e si assiste a un'esplosione dei perfezionamenti tecnici. Si sviluppa di conseguenza un nuovo settore di ricerche per il quale Ph. Dreyfus ha coniato nel 1962 un nuovo termine, informatique (composto di information e automatique), il quale, rispetto alla locuzione inglese computer science, sposta l'accento dallo strumento, l'elaboratore elettronico, all'oggetto immateriale da esso trattato, l'informazione; l'i., nella sua accezione più ampia concerne, oltre le discipline che forniscono la base scientifica e formale (scienze dell'informazione), anche aspetti tecnologici, sistemistici e applicativi. Questa fase di espansione dell'i. è trattata nelle Appendici tra gli anni Settanta e l'inizio dei Novanta, oltre che sotto il lemma informatica, anche nelle voci elettronica (App. IV, i, p. 669 e V, ii, p. 73), elaboratori elettronici (App. IV, i, p. 650 e V, ii, p. 44) oltre che circuito logico (App. IV, i, p. 454), linguaggi programmativi (App. V, iii, p. 215), logica e informatica (App. V, iii, p. 238), intelligenza artificiale (App. V, ii, p. 735). Gli aspetti industriali legati a questo nuovo settore di attività sono descritti nell'App. V nelle voci elettronica, industria (ii, p. 80) e informatica, industria (ii, p. 707).
L'i. ha assunto nel panorama scientifico della fine del 20° sec. una notevole rilevanza, legata alla diffusione dei sistemi di elaborazione nei più svariati ambiti dell'attività umana, dal mondo scientifico, militare, industriale e finanziario, sino al commercio, alla casa, al tempo libero, grazie allo sviluppo della tecnologia digitale dei circuiti integrati (v. microelettronica in questa Appendice), che ha determinato la definitiva affermazione dei computer nella vita quotidiana. Negli ultimi anni sono emerse nuove possibilità di supporto degli strumenti informatici in campo scientifico (v. computazionali, metodi; fisica: Calcolatori nella fisica teorica, e simulazione, in questa Appendice) e umanistico (v. beni culturali: Beni culturali e informatica, e informatica umanistica, in questa Appendice); in particolare hanno avuto notevole sviluppo alcuni settori di i. applicata alla ricerca scientifica (v. informatica medica, App. V, ii, p. 709, ripresa sotto il lemma ingegneria biomedica, e informatica musicale, in questa Appendice; per l'i. giuridica, v. oltre Informatica e diritto). Continuano a estendersi le applicazioni all'ingegneria e all'architettura, anche attraverso lo sviluppo di metodi di rappresentazione numerica dell'informazione applicabili a qualsiasi tipo di segnale. Inoltre, il trattamento di immagini e suoni, anche in forma integrata, ha portato allo sviluppo dell'idea di multimedialità (v. multimedialità; produzione; progettazione; robotica, in questa Appendice). Insieme alla diffusione delle telecomunicazioni, l'onnipresenza degli elaboratori e delle loro applicazioni ha determinato una svolta epocale nei sistemi socioeconomici dei paesi tecnologicamente avanzati, con il passaggio da una società basata sulla produzione industriale e sul consumo di energia a una basata sulla produzione di beni immateriali e di servizi, che viene suggestivamente definita 'società dell'informazione'. In questa voce vengono considerate le sfide teoriche che sono di fronte alle scienze dell'informazione, che forniscono i principi di base dello sviluppo dell'i., oltre che le prospettive del complesso delle tecnologie dell'informazione (v. anche elaboratori elettronici, in questa Appendice). La pervasività dei sistemi informatici ha importanti implicazioni giuridico-sociali, che sono illustrate in conclusione della voce attraverso il rapporto fra i. e diritto. Notevoli sono inoltre le implicazioni socio-culturali della simbiosi fra i. e telecomunicazioni, che ha portato alla nascita delle reti di informazioni e della rete globale Internet (v. rete, in questa Appendice; e nell'App. V le voci telematica, v, p. 417 e spazio informatico, v, p. 94). *
Scienze dell'informazione
di Giorgio Ausiello
Con la locuzione scienze dell'informazione (coniata intorno al 1970 in occasione dell'istituzione presso l'università di Pisa del primo corso di laurea italiano in i.) ci si riferisce a un complesso di discipline scientifiche aventi per oggetto lo studio formale degli strumenti, dei metodi e dei processi per la rappresentazione dell'informazione e per la sua elaborazione. Favorendo la comprensione dei diversi aspetti e delle diverse fasi dell'elaborazione elettronica, le scienze dell'informazione creano le basi concettuali e culturali dello sviluppo tecnologico e contribuiscono a migliorare l'affidabilità, l'efficienza e la facilità d'uso dei sistemi.
Tuttavia, anche se le scienze dell'informazione si occupano prevalentemente di elaborazione dell'informazione realizzata mediante calcolatore elettronico, e si sono sviluppate in relazione all'evoluzione dei calcolatori stessi, va sottolineato che molte problematiche da esse studiate sono indipendenti dallo strumento utilizzato per l'elaborazione. Da un lato queste discipline riguardano temi oggetto di studio anche prima dell'avvento degli elaboratori elettronici (per es., il concetto di algoritmo); dall'altro esse devono affrontare anche aspetti di elaborazione dell'informazione realizzata con tecnologie diverse da quella elettronica (per es., l'elaborazione realizzabile con materiale genetico o con una struttura neuronale). È dunque riduttivo considerare le scienze dell'informazione come le discipline scientifiche alla base dello studio dell'elaboratore elettronico. Esse investono un più vasto ambito culturale; fanno proprie metodologie della fisica (nell'analisi e nella misura dei fenomeni computazionali), della matematica (nella creazione di sistemi formali, modelli, teorie per rappresentare le diverse realtà che si vogliono automatizzare), della psicologia (nella ricerca sui processi cognitivi e sulla loro simulazione).
Due aspetti mettono in evidenza, in particolare, il legame tra le scienze dell'informazione, la matematica e la logica. Per analizzare e affrontare in modo scientifico i problemi relativi all'elaborazione dell'informazione nei vari campi applicativi, è necessario seguire procedimenti di astrazione e di formalizzazione concettualmente non dissimili da quelli seguiti dai matematici ma basati su nuove strutture formali, diverse da quelle utilizzate nei campi classici della matematica. Così, per es., per descrivere e ottimizzare i sistemi di produzione industriale è stata utilizzata la teoria delle reti di Petri, per il controllo di sistemi in condizioni di incertezza sono stati introdotti gli insiemi sfumati (fuzzy sets), per garantire la sicurezza delle transazioni elettroniche è stata sviluppata la teoria dei protocolli crittografici ecc. In questo senso, dunque, le scienze dell'informazione costituiscono un'estensione della matematica per modellare la realtà delle tecnologie informatiche e delle loro applicazioni. Inoltre, si deve tenere presente che le scienze dell'informazione hanno come oggetto di studio anche, o soprattutto, attività caratteristiche della sfera intellettuale dell'uomo: il calcolo, l'analisi di strutture linguistiche, la rappresentazione simbolica della realtà, il ragionamento ecc. Lo studio dei principi logico-matematici che regolano tali attività è dunque un obiettivo non secondario delle scienze dell'informazione, di grande interesse culturale ed epistemologico. Esso costituisce di fatto una prosecuzione e un arricchimento dell'opera dei logici che negli anni Trenta hanno affrontato e risolto i primi importanti interrogativi riguardanti la completezza e la consistenza delle teorie logiche e il potere computazionale dei sistemi formali di calcolo, a partire dalla definizione formale di A.M. Turing del concetto di algoritmo mediante un modello di calcolo astratto (v. informatica, App. IV; logica e informatica, App. V).
In prosecuzione di questa linea di studi a carattere metateorico, lo sviluppo dell'i. ha determinato ulteriori approfondimenti dei concetti e delle proprietà del calcolo, delle macchine, dei linguaggi ecc. Esempi di problematiche affrontate nell'ambito delle scienze dell'informazione e poste su questo piano fondazionale sono: la definizione del concetto di trattabilità computazionale (come raffinamento del concetto di calcolabilità), l'analisi del potere computazionale di nuovi modelli di calcolo (non deterministici, probabilistici, quantistici), la caratterizzazione dei problemi risolvibili vantaggiosamente con calcolatori paralleli, l'analisi delle relazioni esistenti tra costi di elaborazione e costi di comunicazione nel calcolo distribuito ecc.
Aree metodologiche
In relazione ai diversi obiettivi di studio e alle diverse problematiche citate, si sono sviluppate, nell'ambito delle scienze dell'informazione, varie discipline. Lo Handbook of theoretical computer science, opera enciclopedica che al volgere degli anni Novanta ha inteso fornire un quadro aggiornato delle scienze dell'informazione, cita, in proposito, le seguenti aree fondamentali: complessità di calcolo, complessità di descrizione, algoritmi e strutture di dati, geometria computazionale, crittografia, teoria delle reti di comunicazione, teoria dei circuiti ad alta integrazione, architetture e algoritmi paralleli, teoria degli automi e dei linguaggi formali, automi su strutture infinite, sistemi di riscrittura, λ-calcolo e programmazione funzionale, programmazione logica, teorie logiche della programmazione, correttezza dei programmi, logiche modali e temporali, teoria delle basi di dati, teoria dei sistemi distribuiti, teoria dei processi concorrenti. Si tratta, come si vede, di una pluralità estremamente ampia (e peraltro non esaustiva) di tematiche, nell'ambito di ciascuna delle quali si sono sviluppate delle vere e proprie teorie scientifiche, dotate di complessi apparati concettuali, di tecniche di analisi, di strumenti deduttivi logico-formali, di risultati fondamentali, di applicazioni. Nell'impossibilità di fornire, in questa sede, un quadro così ampio, ci limitiamo a presentare alcune delle più importanti tra le suddette tematiche, raccogliendole in due filoni culturali, uno riguardante gli aspetti relativi alla complessità dei problemi e alla progettazione di algoritmi efficienti, l'altro riguardante gli aspetti relativi al comportamento dei programmi e dei processi, che possiamo denominare, rispettivamente, teoria degli algoritmi e della complessità di calcolo e teoria dei programmi e dei processi di calcolo.
Un filone importante nell'ambito delle scienze dell'informazione (già trattato in App. IV: v. informatica: Informatica matematica, teoria dei linguaggi) è costituito dalla teoria degli automi e dei linguaggi formali, che si occupa delle proprietà sintattiche dei linguaggi, intesi come insiemi di sequenze di simboli definite su un dato alfabeto (chiamate stringhe o parole), dei sistemi formali per la loro caratterizzazione e generazione (grammatiche), della struttura e del potere computazionale di modelli elementari di macchine (automi) che consentono di decidere se una stringa appartiene a un dato linguaggio, cioè se essa rispetta determinate proprietà sintattiche. Tale teoria è alla base degli studi relativi alla sintassi dei linguaggi di programmazione, in particolare dei linguaggi detti ad alto livello, cioè dotati di un repertorio concettuale più composito, e ai metodi di verifica della correttezza sintattica dei programmi e di traduzione di essi in sequenze di istruzioni più semplici direttamente eseguibili dal calcolatore.
Teoria degli algoritmi e della complessità di calcolo
In molte applicazioni dell'i. (controllo di impianti, applicazioni aerospaziali, gestione di reti di telecomunicazione, sistemi di grafica interattiva e di realtà virtuale) la tempestività della risposta del sistema di elaborazione è una condizione vincolante per il funzionamento dell'applicazione stessa. Peraltro, anche nei casi in cui non si richiedono tempi di risposta particolarmente stringenti, come per es. nei sistemi di previsione finanziaria o meteorologica, l'efficienza dei programmi è resa necessaria dalla grande mole di dati che devono essere elaborati in breve tempo.
Per accelerare la soluzione di un problema è sempre possibile accrescere la potenza dei mezzi di calcolo utilizzati. L'evoluzione tecnologica ha determinato, nella seconda metà del Novecento, un costante raddoppio della velocità degli elaboratori ogni diciotto mesi, e ciò consente di gestire in tempi più rapidi applicazioni notevolmente più complesse di quelle affrontate in passato. Inoltre, molte applicazioni si possono giovare dell'utilizzazione di calcolatori paralleli in cui il compito elaborativo è suddiviso tra più unità di elaborazione interconnesse in modo più o meno stretto e operanti simultaneamente (v. elaboratori elettronici, in questa Appendice). D'altra parte queste evoluzioni non riducono l'importanza dell'efficienza degli algoritmi, poiché la complessità e la dimensione delle applicazioni richieste è anch'essa aumentata negli ultimi decenni del secolo, accrescendo vieppiù, anziché ridurla, la forbice tra prestazioni offerte dai sistemi e prestazioni desiderate dagli utenti. Infine, come vedremo oltre, problemi di elevata complessità possono trarre poco vantaggio da aumenti anche cospicui della potenza degli elaboratori.
La necessità di garantire, nelle applicazioni informatiche, la maggiore efficienza possibile, compatibilmente con l'intrinseca complessità delle applicazioni, ha portato allo sviluppo di una serie di metodologie volte a studiare tecniche per il progetto di algoritmi efficienti e per l'analisi delle loro prestazioni (anche con riferimento a elaboratori di diversa tecnologia, come i calcolatori paralleli), nonché a individuare la complessità intrinseca dei problemi e a classificare questi ultimi in relazione al costo (quantità di tempo di calcolo o quantità di memoria) necessario per la loro risoluzione.
Analisi del costo di esecuzione di algoritmi
Per analizzare il costo di esecuzione di un algoritmo e la complessità dei problemi è necessario fare riferimento a modelli di calcolatori astratti, semplificati, che consentano di prescindere dalle caratteristiche tecnologiche dei calcolatori utilizzati in pratica e dai dettagli realizzativi con cui l'algoritmo può essere scritto in un reale linguaggio di programmazione.
Il modello astratto utilizzato più frequentemente a questo scopo è la macchina a registri (chiamata anche RAM, Random Access Machine, cioè macchina con memoria ad accesso casuale). Tale modello (direttamente ispirato al modello strutturale dei normali calcolatori, detto anche modello di von Neumann) è dotato di un nastro di ingresso, di un nastro di uscita, di una memoria costituita da un numero potenzialmente illimitato di celle (chiamate registri), ciascuna delle quali capace di contenere numeri interi arbitrariamente grandi, e di un'unità di elaborazione capace di eseguire semplici istruzioni logico-aritmetiche sugli interi contenuti nei registri (non molto dissimili da quelle previste dai calcolatori reali: trasferimento di dati, somma, sottrazione, prodotto, verifica di uguaglianza a zero ecc.).
Per studiare il costo di esecuzione di un algoritmo si può redigere un programma che lo realizza utilizzando le istruzioni elementari previste dalla RAM e valutare poi il costo di esecuzione di tale programma da parte della macchina, contando le istruzioni che vengono eseguite in funzione dei dati in ingresso. Attribuendo opportunamente i costi alle singole istruzioni (in particolare assumendo che il costo di ogni istruzione sia linearmente proporzionale al numero di cifre degli operandi) si può fare in modo che il costo complessivo di esecuzione dell'algoritmo da parte della RAM corrisponda, a meno di costanti moltiplicative, al tempo di esecuzione dell'algoritmo su una macchina reale.
Un altro modello astratto frequentemente utilizzato negli studi di complessità computazionale è la macchina di Turing. Tale macchina dispone di una memoria interna con un numero finito di stati e di un nastro (memoria esterna) suddiviso in celle, e potenzialmente illimitato, su cui la macchina può leggere e scrivere caratteri mediante un'apposita testina di lettura e scrittura. Un passo elementare di calcolo consiste nella lettura di un carattere sul nastro e, in base al carattere letto e allo stato interno in cui la macchina si trova, nell'effettuazione delle seguenti ulteriori operazioni (transizioni di stato): scrittura di un nuovo carattere, passaggio a un altro stato interno e spostamento a destra o a sinistra della testina. Nonostante questo modello sia alquanto lontano dai reali elaboratori, esso è stato ed è tuttora molto utilizzato, sia nella teoria degli automi e dei linguaggi formali, sia nella teoria degli algoritmi per la sua grande semplicità formale e perché, rispetto alla RAM, si presta, in modo più naturale, all'analisi di algoritmi per linguaggi formali.
Lo scopo dell'analisi di algoritmi è di valutare come evolve il costo di esecuzione di un algoritmo per la soluzione di un problema dato, al crescere della quantità e della dimensione dei dati in ingresso (numero di cifre che costituiscono, in notazione decimale o binaria, i dati in ingresso o altre grandezze analoghe: numero di elementi di un vettore, lunghezza di una stringa di caratteri ecc.), e per confrontarne le prestazioni con quelle di altri algoritmi. In casi particolarmente semplici essa può essere effettuata anche esaminando un programma scritto in linguaggio ad alto livello e limitandosi a contare le istruzioni più significative che vengono eseguite durante il calcolo, sempre in funzione della dimensione dei dati in ingresso. L'analisi può fare riferimento sia al comportamento dell'algoritmo in corrispondenza di quei dati per cui l'esecuzione è più laboriosa (analisi del caso peggiore), sia alla media dei costi di elaborazione, assumendo opportune ipotesi di distribuzione dei dati (analisi del caso medio). Per esprimere il comportamento asintotico del costo di esecuzione si utilizza la seguente notazione matematica: si dice che il costo nel caso peggiore (o nel caso medio) è O(f(n)) se esistono due costanti c e n' tali che per ogni n>n', per ogni dato (o, rispettivamente, in media sui dati) di dimensione n, l'algoritmo ha un costo limitato da c f(n).
Per effettuare l'analisi degli algoritmi, in particolare per l'analisi del caso medio, è necessario affrontare, a volte, problemi di natura matematica e combinatoria alquanto complessi (risoluzione di relazioni di ricorrenza mediante funzioni generatrici, espansione delle soluzioni in serie formali, determinazione di approssimazioni asintotiche mediante metodi di analisi complessa ecc.). Tra i ricercatori che hanno maggiormente contribuito a questo campo segnaliamo D.E. Knuth (cui si devono i primi studi e la nozione stessa di analisi di algoritmi), P. Flajolet, R. Sedgewick.
Esempio. Consideriamo il problema dell'ordinamento di un vettore di n interi (per es. in modo crescente). Un metodo banale, chiamato ordinamento mediante selezione, consistente nel cercare via via il minimo tra gli elementi non ancora ordinati e disporlo progressivamente nel vettore, richiede in ogni caso O(n²) confronti tra elementi. Un metodo decisamente preferibile (almeno da un punto di vista asintotico) è quello chiamato ordinamento mediante fusione che consiste nel suddividere il vettore in due parti uguali, nell'ordinare separatamente con lo stesso metodo le due metà e nel fondere i vettori ordinati così ottenuti. Il costo C(n) di questo metodo è O(n logn), dove logn indica il logaritmo in base 2 di n, e si ottiene risolvendo la semplice relazione di ricorrenza C(n)=2 C(n/2)+n, direttamente ricavabile dalla struttura ricorsiva dell'algoritmo. Un altro metodo ricorsivo, che però ha prestazioni diverse nel caso peggiore e nel caso medio, è il metodo chiamato ordinamento rapido. Esso consiste nello scegliere un elemento, individuare la posizione h che gli compete nell'ordinamento finale, e procedere a ordinare con lo stesso metodo i due sottovettori costituiti da elementi in posizione minore e maggiore di h. Questo metodo ha un costo O(n²) nel caso peggiore e O(n logn) nel caso medio. L'analisi del costo nel caso medio per questo algoritmo porta alla relazione di ricorrenza C(n)=n+1+2/n Σj≤nC(j−1), molto più complessa della precedente, e la cui soluzione si basa su un'approssimazione dei numeri armonici.
Tecniche di progetto di algoritmi efficienti. - La necessità di risolvere problemi con metodi efficienti non è emersa solo nell'ambito delle scienze dell'informazione. Da quando hanno cominciato a essere utilizzati i primi calcolatori, tecniche algoritmiche di grande rilevanza sono state sviluppate nell'ambito del calcolo numerico (per la risoluzione di sistemi di equazioni differenziali e integrali) e della ricerca operativa (per la risoluzione di problemi di ottimizzazione). Tuttavia, nell'ambito delle scienze dell'informazione sono state sviluppate, negli ultimi decenni del 20° sec., tecniche di progetto di algoritmi che hanno permesso di migliorare notevolmente le prestazioni degli algoritmi utilizzati in tutti i campi applicativi. In questa sede ci limiteremo a citare alcuni esempi legati a tre importanti tecniche di progetto.
1) Divide et impera. Con questo sintagma è nota la tecnica di risoluzione di problemi basata sulla decomposizione in sottoproblemi. Un elementare esempio di applicazione di questo metodo di progetto è costituito dall'algoritmo di ordinamento mediante fusione, visto precedentemente. L'uso della tecnica divide et impera ha consentito in molti casi di realizzare algoritmi assai efficienti. Ciò si verifica in particolare quando il numero di sottoproblemi in cui il problema viene decomposto è piccolo e quando la ricomposizione delle loro soluzioni per ricostruire la soluzione del problema originario è semplice (per es., di costo lineare). Inoltre il metodo ha il pregio di facilitare l'analisi delle prestazioni poiché (come abbiamo visto nel caso dell'ordinamento mediante fusione) si può esprimere il costo di esecuzione mediante una relazione di ricorrenza che riflette la struttura ricorsiva dell'algoritmo. Esempi storicamente importanti in cui il metodo divide et impera ha consentito di realizzare algoritmi più efficienti di quelli usati in precedenza sono: l'algoritmo di J.M. Cooley e J.W. Tukey (1965) per la trasformata rapida di Fourier, che può essere realizzata in tempo O(n logn) (v. computazionali, metodi: Applicazioni dell'analisi armonica, in questa Appendice); e l'algoritmo per il prodotto di matrici, dovuto a V. Strassen (1969), che ha permesso per la prima volta di battere il classico algoritmo con tempo di esecuzione O(n³) e di effettuare il prodotto di matrici in tempo O(n²,⁸¹), aprendo così la strada a una serie di miglioramenti che hanno portato D. Coppersmith e S. Winograd (1987) alla realizzazione di algoritmi con tempo di esecuzione O(n²,³⁷⁶). Pur non essendo utilizzabile in pratica, l'algoritmo di Coppersmith e Winograd è asintoticamente il miglior algoritmo noto per il prodotto di matrici e non si sa se possa essere ulteriormente migliorato.
2) Bilanciamento. In molte applicazioni in cui si richiede l'accesso rapido a un'ingente quantità di dati immagazzinati nella memoria principale o nella memoria secondaria è necessario organizzare le informazioni in strutture basate sul concetto di albero bilanciato. Se, per es., associamo opportunamente ai nodi di un albero binario n numeri interi (per es., numeri di matricola di impiegati, collegati alle rispettive informazioni anagrafiche) e se tale albero è bilanciato, cioè il sottoalbero destro e il sottoalbero sinistro hanno 'quasi' lo stesso numero di nodi, è possibile reperire le informazioni riguardanti un impiegato in tempo O(log₂ n). Nel caso che si faccia uso di alberi m-ari (cioè tali che ogni nodo interno abbia m figli) si possono ottenere prestazioni ancora migliori perché l'accesso diviene proporzionale al logm n. Nel 1972 è stata proposta da R. Bayer ed E. McCreight una struttura organizzativa delle informazioni basata su alberi m-ari (B-alberi), che consente di effettuare efficientemente la gestione di grandi archivi su memoria secondaria e di ricercare (ed eventualmente inserire o eliminare) un'informazione con un numero molto esiguo di accessi a disco. I B-alberi sono stati utilizzati per realizzare i primi sistemi di basi di dati relazionali e a essi è in gran parte dovuto il successo di tali sistemi. Più recentemente sono state proposte altre strutture di dati, efficienti per la gestione di dati su memoria secondaria, nelle quali il bilanciamento viene garantito realizzando una redistribuzione casuale delle informazioni sulle varie foglie dell'albero (hashing dinamico, hashing lineare ecc.; to hash significa letteralmente 'triturare' e intende suggerire il fatto che un'informazione viene codificata mediante una stringa calcolata da una funzione che tritura e rimescola i caratteri dell'informazione originaria), in modo da eliminare eventuali squilibri esistenti intrinsecamente nell'insieme delle informazioni trattate. Il concetto di bilanciamento si può estendere dal caso della ricerca su archivi a molti altri problemi. In particolare, il bilanciamento tra sottoproblemi è una condizione necessaria per garantire che la decomposizione attuata dal metodo divide et impera dia risultati efficienti.
3) Dinamizzazione. Un numero crescente di applicazioni informatiche richiede la gestione di informazioni con una rapida evoluzione temporale e quindi soggette ad aggiornamenti molto frequenti. Ciò si verifica, per es., nelle reti di telecomunicazioni, nella visione di scene in movimento, nella grafica interattiva ecc. In questi casi, le usuali strutture di organizzazione dei dati nell'elaboratore non offrono le prestazioni richieste. Per tale motivo sono state introdotte strutture di dati dinamiche che possono essere facilmente aggiornate e che garantiscono un buon comportamento, se non a ogni operazione, almeno su un'intera sequenza di operazioni di aggiornamento. Il maggior contributo in questa direzione è stato dato da R.E. Tarjan che, nel corso degli anni Ottanta, ha introdotto varie strutture di dati chiamate autoadattative (in particolare gli 'alberi sghembi', splay trees) che permettono di eseguire efficientemente sequenze di operazioni di interrogazione e di aggiornamento (inserimenti, cancellazioni, fusioni, scomposizioni ecc.). In questi casi si deve utilizzare un metodo di analisi che tenga conto della ripartizione del costo sulle operazioni di una sequenza (analisi ammortizzata). Oltre a rivelarsi un utile paradigma nella gestione di problemi a elevata dinamicità, l'uso di strutture autoadattative ha anche consentito il miglioramento della soluzione di alcuni problemi di ottimizzazione, come per es. il problema della massimizzazione del flusso in una rete, per il quale A.V. Goldberg e lo stesso Tarjan (1986) hanno proposto una soluzione di costo O(nm log(n²/m)) per grafi con n nodi e m archi, trent'anni dopo il classico (ma inefficiente) algoritmo proposto da L.R. Ford e D.R. Fulkerson (1956).
I risultati riguardanti la realizzazione di algoritmi efficienti, ottenuti a seguito dell'intenso sviluppo della ricerca nell'ambito della teoria degli algoritmi e che sarebbero degni di nota per la loro rilevanza pratica, sono innumerevoli. Tra i campi in cui sono stati fatti progressi significativi possiamo ancora citare: la programmazione lineare (un'importante classe di problemi di ottimizzazione, fino a pochi anni fa ritenuta di costo intrinsecamente esponenziale, per la quale sono stati individuati invece algoritmi polinomiali; v. ottimizzazione, in questa Appendice), la gestione ottimale di reti (importante in quest'area è, per es., la realizzazione di un algoritmo lineare per il minimo albero ricoprente di un grafo), la geometria computazionale (per la quale sono stati definiti algoritmi efficienti di localizzazione di punti in regioni dello spazio e di triangolazione di superfici) ecc.
Caratterizzazione della complessità intrinseca dei problemi. - Il concetto di complessità si presenta in varia forma nell'ambito delle diverse discipline scientifiche. In vari contesti, per es., esso viene correlato alle strutture matematiche (equazioni algebriche, differenziali ecc.) necessarie per descrivere sistemi naturali o artificiali. Nel campo delle scienze dell'informazione, con il termine complessità ci si riferisce, usualmente, alla complessità computazionale, cioè al costo computazionale (quantità di tempo o di memoria) necessario e sufficiente per risolvere un problema con un determinato modello di calcolo (per es. RAM o macchina di Turing).
Per determinare esattamente la complessità computazionale di un problema si deve poter asserire che, fatto riferimento a un particolare modello di calcolo (per es., la RAM), esiste un algoritmo che risolve il problema dato con un certo costo, e che nessun algoritmo può risolvere il problema stesso con un costo asintoticamente minore. La conoscenza di un algoritmo risolutivo per un dato problema non è dunque sufficiente per determinare la complessità del problema stesso. Il costo di esecuzione dell'algoritmo, infatti, fornisce una delimitazione superiore della complessità del problema, ma non ci dice nulla sulle intrinseche caratteristiche che rendono più o meno difficile la soluzione del problema stesso e che derivano dalla sua natura combinatoria. È lo studio di queste proprietà che permette di individuare il costo necessario per risolvere il problema, di individuare, cioè, una delimitazione inferiore della sua complessità. Quando tali delimitazioni coincidono vuol dire che abbiamo caratterizzato esattamente la complessità del problema e che, quindi, l'algoritmo risolutivo che possediamo ha, da un punto di vista asintotico, prestazioni ottime. Formalmente, diciamo che la complessità di un problema è:
- O(f(n)) se esiste un algoritmo che lo risolve con un costo O(f(n)),
- Ω(f(n)) se ogni algoritmo comporta almeno un costo dell'ordine di f(n),
- Θ(f(n)) se essa è sia O(f(n)) sia Ω(f(n)).
Esempio. Consideriamo ancora il problema dell'ordinamento. Possiamo mostrare che la sua complessità è Θ(n logn). Infatti essa è Ω(n logn) poiché il numero di possibili ordinamenti di un vettore di n elementi è n! e il numero minimo di confronti necessari per individuare l'ordinamento corretto è log(n!) ≈̳ n logn (ogni confronto può al più suddividere in due semispazi di uguale cardinalità lo spazio degli ordinamenti possibili). D'altra parte, come abbiamo visto, l'algoritmo di ordinamento mediante fusione è in grado di operare con un costo O(n logn). Possiamo dunque concludere che la complessità del problema dell'ordinamento è Θ(n logn) e che l'algoritmo suddetto è ottimo.
In base alla loro complessità, i problemi vengono raggruppati in classi. Per es., i problemi che hanno complessità O(nk) per qualche valore di k costituiscono la classe dei problemi risolubili in tempo polinomiale, denominata classe P. Tipici esempi di problemi appartenenti a P sono l'ordinamento di vettori, la moltiplicazione di matrici, la determinazione di cammini minimi in grafi e reti, la programmazione lineare ecc. Si noti che, poiché RAM e macchine di Turing possono simularsi reciprocamente in tempo polinomiale, se un problema appartiene alla classe P non dobbiamo specificare a quale modello di calcolo facciamo riferimento.
Altre classi significative (fra le molte che sono state studiate) sono le classi di problemi risolubili in tempo esponenziale (EXP), e quelle dei problemi che richiedono una quantità di spazio (memoria) logaritmica (LOGSPAZIO) o polinomiale (PSPAZIO).
Le classi di complessità temporale e spaziale sono parzialmente ordinate rispetto all'inclusione, e lo studio della struttura di tale ordinamento (chiamato complessità strutturale) costituisce uno dei capitoli più importanti delle scienze dell'informazione.
Al centro dell'interesse della complessità strutturale si trova il concetto di trattabilità computazionale. Tale concetto costituisce un rafforzamento del concetto di calcolabilità: un problema si dice trattabile se non solo è possibile risolverlo in modo algoritmico (cioè esso è calcolabile) ma la sua soluzione è realizzabile con un algoritmo che ha un costo di esecuzione polinomiale ed è quindi possibile risolverlo efficientemente in pratica. I problemi la cui soluzione richiede tempo crescente in modo non limitato da un polinomio (per es., in modo esponenziale) vengono considerati intrattabili poiché per essi la crescita asintotica del costo di elaborazione rende proibitiva la risoluzione non appena i dati in ingresso raggiungono una dimensione ragguardevole.
La scelta di identificare la trattabilità computazionale con la complessità polinomiale può apparire arbitraria. Per comprendere tale scelta si può osservare che i benefici derivanti dal potenziamento dei mezzi di elaborazione incidono soprattutto nel caso di problemi risolubili in tempo polinomiale, ma arrecano poco giovamento nella risoluzione di problemi che comportano tempi di risoluzione esponenziali. Infatti, l'utilizzazione di p elaboratori in parallelo (o l'aumento della potenza di un singolo elaboratore di un fattore p) nella migliore delle ipotesi non può che ridurre dello stesso fattore p il tempo di elaborazione complessivo. Sia, per es., p=1024. Supponiamo che in una certa quantità di tempo (diciamo un secondo) sappiamo risolvere un caso di un problema di dimensione k. Ebbene, se il costo della soluzione del problema cresce come n², un calcolatore parallelo con p unità potrà permetterci di affrontare, nella stessa quantità di tempo, un caso di dimensione 32k, ma se il problema richiede tempo dell'ordine di 2n, il calcolatore con p unità permetterà al più di risolvere, sempre nell'intervallo di un secondo, casi di dimensione n+10 e il vantaggio conseguito sarà quindi marginale.
Iniziatori della teoria della complessità computazionale, a metà degli anni Sessanta, si possono considerare J. Hartmanis, H. Stearns e H.R. Lewis, i quali hanno mostrato le condizioni che permettono di provare l'inclusione stretta tra le classi temporali e tra le classi spaziali (teoremi di gerarchia). A tali studi hanno fatto seguito quelli di M. Blum e A. Meyer, aventi per oggetto le proprietà astratte (indipendenti da specifici modelli di calcolo) del concetto di misura di complessità e di classe di complessità, e successivamente, negli anni Settanta, le ricerche di W.J. Savitch, S. Cook, R. Karp, D. Johnson, L. Levin e altri, volte a caratterizzare (anche mediante modelli di calcolo non deterministici, in cui cioè le computazioni non sono costituite da una sequenza univoca di passi ma si diramano con una struttura ad albero) la complessità di problemi di rilevante interesse applicativo e a studiarne la trattabilità. Nonostante i molti risultati conseguiti nell'ambito della teoria della complessità, vari aspetti irrisolti, di interesse sia strutturale che applicativo, pongono all'inizio del nuovo secolo importanti interrogativi agli studiosi. Tali interrogativi investono la natura stessa del calcolo, come, per es., quello riguardante la relazione esistente tra le principali risorse di calcolo, in particolare spazio e tempo: nonostante il primo (a differenza del secondo) sia riusabile, allo stadio attuale non è provato che PSPAZIO contenga funzioni non in P. Anche la relazione tra LOGSPAZIO e P costituisce un interessante problema aperto, poiché non è noto se il contenimento di LOGSPAZIO in P sia stretto o meno.
Una questione di particolare rilevanza riguarda la trattabilità o intrattabilità di un'ampia classe di problemi per i quali si conoscono solo algoritmi di costo temporale esponenziale ma, al tempo stesso, si conoscono solo delimitazioni inferiori di complessità polinomiali. Alcuni esempi di problemi di tale tipo sono la risolubilità di un sistema di equazioni lineari a variabili intere, la soddisfattibilità di un'espressione booleana, la possibilità di sequenziare un insieme di lavori su più macchine in modo da rispettare una data scadenza, la possibilità di stabilire se esiste un percorso che consenta a un commesso viaggiatore di visitare un dato numero di città entro un dato limite di tempo ecc.
Una particolarità comune a tutti questi problemi è che in ogni caso l'insieme delle soluzioni possibili (per es., l'insieme di tutte le possibili assegnazioni di valori di verità alle variabili della formula booleana o l'insieme di tutti i percorsi diversi che possono essere seguiti dal commesso viaggiatore) è esponenziale, mentre la verifica del fatto che una data soluzione soddisfi la proprietà richiesta (cioè che una data assegnazione di valori di verità soddisfi la formula o che il commesso viaggiatore completi il suo viaggio nel tempo richiesto) può essere effettuata in tempo polinomiale. La classe dei problemi che hanno questa natura è chiamata NP (poiché essa coincide con la classe di problemi risolubili in tempo polinomiale con una macchina non deterministica). Chiaramente la classe NP contiene la classe P, ma allo stadio attuale non è noto se qualche problema in NP sia effettivamente di complessità non polinomiale (e quindi sia P≠NP) o se non sia possibile trovare, per tutti i problemi in NP, algoritmi di costo polinomiale (e quindi sia P=NP).
In particolare, tra i problemi appartenenti alla classe NP si trovano i problemi detti NP-completi, la cui struttura combinatoria è sufficientemente ricca da permettere che ogni altro problema in NP sia Karp-riducibile a essi, in tempo polinomiale. Un problema A è Karp-riducibile in tempo polinomiale a un problema B se per risolvere un caso del problema A è sufficiente effettuare un'unica chiamata alla procedura che risolve un caso del problema B costruito in tempo polinomiale. In base a tale proprietà (dimostrata da S. Cook nel 1971 per il problema della soddisfattibilità di formule booleane e successivamente dimostrata da R.M. Karp per numerosi altri problemi combinatori), se anche per un solo problema NP-completo si individuasse un algoritmo di costo polinomiale, tutti i problemi in NP sarebbero risolubili in tempo polinomiale e risulterebbe P=NP. La gran maggioranza dei problemi noti in NP sono in effetti NP-completi; per es., sono NP-completi tutti i problemi che sono stati citati precedentemente, e nuovi problemi NP-completi si incontrano quotidianamente in ogni campo dell'i., della matematica e di altri settori scientifici (inclusa la biologia: recentemente è stato mostrato, per es., che alcuni problemi relativi alla struttura delle proteine sono NP-completi). La grande rilevanza applicativa dei problemi che risultano NP-completi, oltre alla loro abbondanza, rende il tentativo di scoprire se sia possibile risolvere tali problemi in tempo polinomiale o, al contrario, di dimostrare che la loro complessità è intrinsecamente esponenziale, una delle principali questioni aperte delle scienze dell'informazione. In fig. 1 presentiamo la struttura gerarchica delle principali classi di complessità.
Metodi di calcolo approssimato. - L'elevata complessità di molti problemi di rilevante importanza, e quindi l'impossibilità di disporre di algoritmi efficienti per la loro soluzione, implica che, quando è necessario affrontare in pratica la soluzione di tali problemi, si debba ricorrere a metodi di soluzione approssimati. Ciò, in particolare, si verifica nel caso dei problemi di ottimizzazione combinatoria in cui alle diverse soluzioni di un problema è associato un valore (mediante una corrispondenza chiamata, in genere, funzione obiettivo) e la finalità dell'elaborazione consiste nel determinare, nello spazio finito ma estremamente ampio delle soluzioni possibili, una soluzione (non necessariamente unica) che massimizzi o minimizzi tale valore. Problemi di tale natura vengono detti NP-ardui (o NP-difficili) se per essi può esistere un algoritmo risolutivo polinomiale solo se risulta P=NP. Se un problema di ottimizzazione è NP-arduo, a fronte di un algoritmo che fornisce una soluzione ottima ma richiede tempo esponenziale, è in molti casi possibile realizzare un algoritmo che determina in tempo polinomiale una soluzione non ottima ma il cui valore può essere prossimo al valore della soluzione ottima.
La risoluzione esatta e approssimata dei problemi di ottimizzazione è uno dei temi più importanti, sia dal punto di vista teorico sia da quello applicativo, nell'ambito della teoria degli algoritmi e della complessità computazionale. Chiamiamo algoritmo di approssimazione a qualità garantita un algoritmo eseguibile in tempo polinomiale che risolve in modo approssimato un problema di ottimizzazione NP-arduo, fornendo sempre una soluzione il cui valore può presentare, rispetto all'ottimo, un errore di entità limitata.
Esempio. Si consideri il seguente problema: data una rete stradale con m strade, si deve determinare il minimo numero di vigili urbani da disporre agli incroci in modo che ogni strada abbia un vigile ad almeno una delle due estremità. Sfruttando le tecniche di riduzione viste precedentemente si può dimostrare che questo problema è risolubile in modo ottimo in tempo polinomiale se e solo se risulta P=NP. Ebbene, è possibile mostrare che, se ci si accontenta di una soluzione approssimata che fa uso di un numero di vigili (al più) doppio rispetto al minimo possibile, si può determinare una soluzione in tempo O(m). A tal fine si può procedere nel seguente modo: si seleziona una strada qualsiasi e si assegnano due vigili agli incroci che sono alle sue estremità. Poi si cancellano dalla rete tutte le strade che portano a tali due incroci e si seleziona un'altra strada. Si procede in tal modo finché tutte le strade sono servite. Non è difficile convincersi che il numero di vigili utilizzati non sarà mai più del doppio del numero minimo necessario; infatti, in qualunque soluzione ottima, ognuna delle strade via via prese in considerazione, a cui sono stati assegnati due vigili, dovrà avere comunque un vigile ad almeno una delle estremità.
Vari problemi di ottimizzazione NP-ardui ammettono, come quello visto nell'esempio, soluzioni approssimate di qualità garantita. Tra di essi sono particolarmente interessanti il problema di massimizzare il numero di clausole soddisfattibili in un'espressione booleana in forma normale congiuntiva (approssimabile a 1/8 dall'ottimo), quello di determinare il massimo taglio in un grafo (approssimabile a poco più del 10% dall'ottimo) e infine quello del commesso viaggiatore, nel caso in cui i costi di percorrenza delle strade che collegano le varie città soddisfino la disuguaglianza triangolare (in tal caso si possono ottenere soluzioni che non eccedono mai più del 50% il costo minimo).
Per alcuni problemi di ottimizzazione le condizioni di approssimabilità sono ancora più forti: per essi, qualunque sia il grado di approssimazione che vogliamo raggiungere, esiste un algoritmo di approssimazione che garantisce tale comportamento. È il caso, per es., del problema (noto come problema della bipartizione) consistente nel dividere un'eredità, costituita di tanti oggetti di valore, ciascuno dei quali non scomponibile, tra due fratelli, in modo da minimizzare la differenza di valore ottenuto da essi. Un altro esempio è il problema (noto come problema della bisaccia) consistente, intuitivamente, nel massimizzare il valore degli oggetti che possono essere inseriti in una bisaccia senza eccedere la capacità della bisaccia stessa.
Sfortunatamente non tutti i problemi di ottimizzazione NP-ardui ammettono algoritmi di approssimazione a qualità garantita poiché, per molti problemi, la ricerca di una soluzione di qualità garantita è altrettanto complessa della ricerca di una soluzione ottima. Ciò accade, per es., per il problema della colorazione ottima di grafi (consistente nella ricerca del minimo numero di colori applicabili ai nodi di un grafo con il vincolo che a nodi adiacenti, cioè collegati da un arco, vengano assegnati colori diversi), per il problema della ricerca della massima cricca in un grafo (cioè la ricerca del massimo numero di nodi di un grafo mutuamente congiunti da un arco) e anche per il problema, già citato, della ricerca del percorso ottimo per il commesso viaggiatore, nel caso in cui non ci siano restrizioni sui costi di percorrenza delle strade.
I motivi che rendono alcuni problemi di ottimizzazione NP-ardui approssimabili e altri no sono solo parzialmente compresi, e la ricerca in questo campo delle scienze dell'informazione, avviata dai lavori di D.S. Johnson negli anni Settanta, è molto stimolante. In particolare, solo agli inizi degli anni Novanta, dopo un ventennio di inutili tentativi, alcuni studiosi (soprattutto S. Arora, S. Safra, M. Sudan) sono riusciti a dimostrare i limiti di approssimabilità o l'eventuale non approssimabilità di alcuni problemi. Le tecniche sviluppate per dimostrare la non approssimabilità si basano su una singolare proprietà degli insiemi NP-completi (teorema delle dimostrazioni verificabili in modo probabilistico). Questa proprietà stabilisce che per ogni insieme NP-completo S, se un elemento e appartiene a S, esiste una dimostrazione di questo fatto (codificata in una sequenza binaria) che può essere verificata, in tempo polinomiale, da un algoritmo che ne esamina solo un numero prefissato di bit, scelti a caso.
L'introduzione di elementi di casualità nella realizzazione di algoritmi è un altro importante strumento che consente, in alcuni casi, di ottenere efficientemente la soluzione di un problema complesso a patto di accettare un limitato rischio di errore. Intuitivamente, un algoritmo che sfrutta la casualità (algoritmo probabilistico, o anche, con termine di derivazione anglosassone, algoritmo randomizzato) può essere realizzato prevedendo che, in occasione di particolari scelte, anziché procedere deterministicamente ci si affidi al lancio di una moneta e si proceda opportunamente a seconda che il risultato sia 'testa' o 'croce'. In realtà, per effettuare scelte casuali in un algoritmo probabilistico si ricorre a un generatore di valori casuali (un singolo bit zero o uno, o un valore in un certo intervallo). Uno dei primi algoritmi probabilistici volti alla soluzione di un problema complesso è l'algoritmo proposto da M.O. Rabin nel 1980 per decidere se un dato numero è un numero composto o è un numero primo (test di primalità), un problema per il quale non è, ancora oggi, noto alcun algoritmo polinomiale.
Definiamo certificato di non primalità di un intero n un altro intero m, con 1〈m〈n, dotato di proprietà tali da garantire che n non è un numero primo. Ovviamente un divisore di n è un certificato di non primalità di n ma molti altri numeri minori di n, oltre ai suoi divisori, possono essere certificati di non primalità. Per es., si può dimostrare che se mn⁻¹ - 1 non è un multiplo di n, allora n è composto. La teoria dei numeri consente di dimostrare che esistono opportune definizioni di certificato di non primalità tali che se un numero non è primo allora il numero di certificati della sua non primalità è maggiore di n/2. Consideriamo ora un algoritmo probabilistico che, dato n, genera a caso m (1〈m〈n) e verifica se esso è un certificato della non primalità di n. Una risposta positiva si verifica solo se n è composto; una risposta negativa si può verificare se n è primo oppure se n non è primo, ma noi abbiamo generato un numero che non è un suo certificato. Poiché ciò avviene con probabilità minore di 1/2, se l'algoritmo, in caso di risposta negativa, dichiara comunque che n è primo, la risposta è corretta con probabilità maggiore di 1/2. Ripetendo la verifica con k successivi valori m₁, ..., mk, si può ottenere una probabilità di errore minore di 1/2k. La probabilità di errore può essere dunque resa arbitrariamente piccola, per es. minore di 1/2¹⁰⁰, un risultato che, a tutti i fini pratici, è equivalente alla certezza.
Per analogia con la terminologia adottata per indicare un metodo di integrazione numerica basato su un approccio probabilistico, un algoritmo di questa natura viene chiamato algoritmo Monte Carlo. Un algoritmo di tale tipo può dare una risposta errata, ma con una probabilità di errore limitata; per es., l'algoritmo per il test di primalità può, con un margine di errore che può essere reso piccolo a piacere, dichiarare che un intero è un numero primo anche se non lo è. In questo caso l'errore si può verificare solo se la risposta è affermativa, mentre se la risposta è negativa (il numero non è primo) essa è sicuramente corretta (errore unilaterale). Esistono peraltro algoritmi Monte Carlo che possono errare sia nel caso di risposte affermative sia nel caso di risposte negative (errore bilaterale). Altri problemi per i quali sono stati realizzati algoritmi probabilistici sono i problemi di ricerca di occorrenze di stringhe in un testo, i problemi di conteggio, di taglio minimo su grafi ecc.
L'utilizzazione di algoritmi probabilistici, tuttavia, non è limitata a questo tipo di applicazioni. L'uso della casualità può risultare utile anche per velocizzare algoritmi. In molti casi, infatti, una redistribuzione casuale delle informazioni in ingresso può rendere con elevata probabilità la soluzione più efficiente. Solo occasionalmente l'algoritmo continuerà ad avere un costo di esecuzione elevato. Per questo tipo di algoritmo è stato adottato il nome di algoritmo Las Vegas. Un esempio di algoritmo Las Vegas è la versione probabilistica dell'algoritmo di ordinamento rapido, già citato precedentemente, nella quale la casualità consente di ottenere un bilanciamento dei sottoproblemi che non è invece garantito dalla versione deterministica dell'algoritmo.
Il potere computazionale degli algoritmi probabilistici di vario tipo è tuttora oggetto di studio. Chiaramente gli algoritmi probabilistici non sono più potenti delle macchine di Turing (è sempre possibile simulare un qualunque tipo di algoritmo probabilistico con una macchina di Turing). Ciò che non è stato caratterizzato, e rappresenta una delle grandi sfide intellettuali che impegneranno la ricerca nel campo delle scienze dell'informazione all'inizio del 21° sec., è il potere degli algoritmi probabilistici operanti in tempo polinomiale. Se chiamiamo RP la classe dei problemi di decisione risolubili in tempo polinomiale con un algoritmo probabilistico che può errare (ma con probabilità inferiore a 1/2) solo quando dovrebbe rispondere positivamente, si può facilmente osservare che P⊆RP⊆NP. Finora però non esiste alcuna dimostrazione che il primo contenimento sia stretto, che, cioè, esista qualche problema intrattabile che può essere risolto in tempo polinomiale ammettendo una limitata possibilità di errore. In altre parole non si sa se la casualità possa realmente aiutare nella risoluzione di problemi complessi. Si osservi che, in base a questa definizione e all'algoritmo discusso precedentemente, il problema di verificare se un numero è composto o è primo appartiene a RP.
In pratica, gli algoritmi probabilistici hanno consentito importanti progressi in moltissimi campi dell'i., in particolare nel campo dei protocolli crittografici che, a loro volta, hanno influenzato settori applicativi importanti come il commercio elettronico, l'accesso elettronico ai servizi bancari, l'utilizzazione di servizi a pagamento su rete come la televisione a richiesta (video-on-demand).
Uno dei più interessanti e promettenti casi di applicazione di algoritmi probabilistici in quest'area riguarda i protocolli interattivi, e in particolare le cosiddette dimostrazioni a conoscenza nulla. In questo tipo di protocolli si ipotizza un dialogo tra un dimostratore P (avente a disposizione illimitate risorse computazionali) e un verificatore V (che può effettuare una qualunque elaborazione probabilistica in tempo polinomiale) in merito a una determinata asserzione. Se l'asserzione è vera, P riesce a convincere V di ciò, senza peraltro trasmettergli alcuna conoscenza relativa al metodo di prova; se l'asserzione è falsa, anche barando, P non riuscirebbe a convincere V della correttezza dell'asserzione con probabilità maggiore di 1/2. La nozione di dimostrazioni a conoscenza nulla è stata introdotta da S. Goldwasser, S. Micali e C. Rackoff, intorno alla metà degli anni Ottanta; indipendentemente, nello stesso periodo, L. Babai ha introdotto un analogo tipo di protocolli chiamati giochi tra Artù e Merlino.
Esempio. Consideriamo il problema del non isomorfismo di grafi. Dati due grafi G₁ e G₂ ci si chiede se non esista una permutazione π dei nodi tale che se (e solo se) in Gi esiste un arco (ni, nj), in G₂ esiste un arco (nπ(i), nπ(j)). Il protocollo funziona nel seguente modo:
V sceglie a caso i in {1,2} e una permutazione π;
calcola H=π(Gi);
fornisce H a P e chiede a P un indice j in {1,2} tale che H sia isomorfo a Gj;
P restituisce un indice j;
V accetta che G₁ e G₂ sono non isomorfi se j=i, rifiuta altrimenti.
Vediamo, in modo informale, perché l'algoritmo opera correttamente. Supponiamo che V scelga i=1. Supponiamo poi che i grafi non siano isomorfi. Allora P non può che rispondere con j=1 e quindi V deve necessariamente accettare, nel 100% dei casi. Supponiamo, invece, che i grafi siano isomorfi. In tal caso non c'è alcuna possibilità che P risponda 1 con probabilità maggiore del 50%. Ripetendo eventualmente il protocollo si può ottenere che il margine di errore scenda dal 50% a un valore arbitrariamente piccolo.
I protocolli interattivi e gli algoritmi probabilistici che ne sono alla base hanno avuto un ruolo molto importante nell'ambito delle scienze dell'informazione per quanto attiene il problema teorico della caratterizzazione di classi di complessità: per es., abbiamo già visto che la classe NP può essere caratterizzata mediante un tipo particolarmente semplice di protocollo interattivo, le dimostrazioni verificabili in modo probabilistico, e un risultato analogo, con un opportuno protocollo, vale per la classe PSPAZIO. Inoltre essi sono stati decisivi anche da un punto di vista pratico nello sviluppo delle moderne tecniche crittografiche.
Teoria dei programmi e dei processi di calcolo
La soluzione di problemi mediante elaboratore richiede come prima condizione che i programmi utilizzati effettuino correttamente le operazioni per le quali sono stati progettati. Nonostante siano trascorsi più di quarant'anni dall'invenzione dei primi linguaggi di programmazione ad alto livello (v. linguaggi programmativi, App. V), e nonostante i grandi progressi compiuti con la diffusione di metodologie di progetto e sviluppo di programmi, il problema della correttezza funzionale del software rimane un problema aperto. Mentre gli elaboratori si diffondono in tutti i settori, e in particolare in ambito industriale e commerciale, nella generalità dei casi la rilevazione di errori avviene ancora con metodi di verifica empirici, consistenti nel provare il comportamento del programma su particolari sequenze di dati di ingresso; a volte, gli errori presenti vengono individuati solo a seguito dei malfunzionamenti da essi determinati. Ciò, in parte, è dovuto a limitazioni intrinseche evidenziate dalla teoria delle calcolabilità e consistenti nella indecidibilità di molti problemi di verifica delle proprietà di programmi (per es., la terminazione). Tuttavia, questa situazione è anche dovuta al fatto che non sono stati ancora adottati su larga scala i metodi formali di verifica applicabili ai casi decidibili. Infatti, mentre dal punto di vista sintattico i linguaggi di programmazione sono accompagnati, in genere, da una definizione formale che ne consente un uso corretto, dal punto di vista semantico, cioè del significato delle istruzioni, essi sono accompagnati da una descrizione informale, incompleta, a volte inconsistente e, spesso, dipendente dal compilatore utilizzato.
Il problema di definire una precisa semantica di un linguaggio e di garantire la correttezza di funzionamento del software è divenuto ancora più complesso da quando si è affermato l'uso di applicazioni distribuite, da quando cioè, anziché risiedere su un unico elaboratore, le applicazioni hanno cominciato a essere localizzate su più elaboratori, dislocati nei vari reparti di un'azienda o di un ufficio e collegati in 'rete locale'. Più recentemente, per alcune applicazioni in ambito Internet, si è addirittura rinunciato alla località dei programmi a favore dell'uso di codice mobile tra elaboratori dislocati a centinaia o migliaia di chilometri l'uno dall'altro e collegati in reti globali. Uno scenario applicativo che sarà sempre più diffuso nei futuri anni vedrà la realizzazione di compiti (telelavoro, teledidattica, commercio elettronico) da parte di programmi mobili (agenti) che potranno interagire in vario modo con altri agenti mossi da intenti cooperativi od ostili (v. oltre: Le tecnologie per i sistemi distribuiti).
Nell'area che abbiamo denominato teoria della programmazione e dei processi di calcolo esistono vari approcci allo studio del comportamento dei programmi e delle loro possibili interazioni. Tali approcci sono basati sulla definizione formale del comportamento dei programmi mediante modelli astratti e hanno diverse finalità: dotare i linguaggi di programmazione di vario tipo (sequenziali, paralleli, concorrenti) di una semantica formale definita in modo altrettanto rigoroso di quanto è definita la sintassi; consentire prove formali di correttezza dei programmi rispetto alla specifica fornita dall'utente; definire e studiare nuovi concetti e paradigmi di programmazione che agevolino la produzione di software corretto e affidabile. Per questi ultimi aspetti, gli studi nel campo della teoria della programmazione hanno un ruolo significativo nei confronti delle aree più applicative dei linguaggi, delle metodologie e degli ambienti di programmazione che formano la cosiddetta ingegneria del software.
Semantica operazionale. - Un primo approccio allo studio del comportamento di un programma consiste nella definizione di un modello di calcolo astratto (macchina astratta) e nella rappresentazione dei passi di calcolo del programma in tale modello (semantica operazionale). In tal modo è possibile prescindere da quegli aspetti di comportamento che dipendono dalle caratteristiche tecnologiche della macchina utilizzata e concentrarsi, in prima istanza, sugli aspetti del comportamento legati al linguaggio di programmazione. Gli aspetti tecnologici (per es., lunghezza massima delle costanti numeriche prevista dalla dimensione della memoria) potranno poi essere reintrodotti come parametri della semantica formale.
In un approccio molto utilizzato, basato su un punto di vista sintattico, il modello è costituito da tutte le espressioni (termini) costruibili con i simboli di funzione e i simboli di variabile disponibili nel linguaggio. In logica, l'insieme dei termini viene chiamato universo di Herbrand. Formalmente ogni simbolo di variabile x₁,...,xn è un termine e, per ogni simbolo di funzione fi , con mi argomenti, se t₁,...,tmi sono termini, anche l'espressione fi (t₁,..., tmi) è un termine. In particolare, i simboli di funzione con zero argomenti sono chiamati costanti. Per es., se f è una funzione unaria, x è una variabile e O una costante, avremo che i possibili termini sono la costante O, la variabile x e la funzione f applicata a un termine. In tal caso l'universo di Herbrand è costituito dall'insieme: {O, x, f(O), f(x), f(f(O)), f(f(x)),...}. I passi di calcolo corrispondenti alle varie istruzioni del linguaggio sono descritti mediante regole di sostituzione (riscrittura) di termini con altri termini. Per es., le seguenti due regole di riscrittura definiscono il comportamento del costrutto if-then-else:
if true then T₁ else T₂→T₁
if false then T₁ else T₂→T₂
La loro applicazione determina la sostituzione del termine al lato sinistro della freccia con quello al lato destro, indipendentemente dai termini T₁ e T₂. L'esecuzione delle istruzioni di un programma (computazione) corrisponde a una serie di passi di riscrittura che si conclude quando si giunge a un termine che non ammette più sostituzioni (interpretabile come un valore costante nel dominio dei dati: un intero, un valore booleano ecc.), o può non concludersi, se si entra in una serie ciclica di sostituzioni.
Una classica applicazione di questo approccio è volta allo studio dei meccanismi di chiamata di funzione e di esecuzione della ricursione nei linguaggi di programmazione. A seconda delle regole adottate per gestire la valutazione di funzioni (per es., regole di sostituzione che partono dall'interno di un termine o regole di sostituzione che partono dall'esterno) si possono avere, infatti, risultati diversi. Per determinati argomenti, una funzione può essere definita se valutata secondo alcune regole, e non definita se valutata secondo altre.
Semantica denotazionale. - Un inconveniente delle semantiche operazionali è il fatto che esse dipendono dal modello di macchina astratta utilizzato. Un approccio che si prefigge di caratterizzare il comportamento di un programma definendo invece direttamente in termini matematici la funzione che esso calcola nel dominio dei dati, a partire dalla struttura sintattica del programma stesso, è l'approccio chiamato semantica denotazionale (inizialmente chiamato semantica matematica), introdotto da D. Scott e C. Strachey nel 1971.
Nella semantica denotazionale ogni struttura sintattica composta di un programma viene associata a un oggetto matematico, chiamato denotazione (per es., la funzione che quella particolare struttura definisce), che deriva esclusivamente dalle denotazioni delle sottostrutture componenti (proprietà di composizionalità). A strutture elementari corrispondono oggetti matematici primitivi (funzioni base). La funzione definita da un programma viene così individuata con un meccanismo di induzione strutturale. Una delle caratteristiche dell'approccio denotazionale è l'uso del concetto di punto fisso. Come domini dei dati si assumono, anziché insiemi, insiemi parzialmente ordinati completi e, potendosi interpretare i programmi di un linguaggio di programmazione come funzionali continui su tali insiemi, è possibile garantire l'applicabilità del teorema del punto fisso di Knaster-Tarski e individuare le funzioni calcolate da programmi ricorsivi come i punti fissi associati a tali programmi.
L'approccio denotazionale ha il pregio di una notevole eleganza formale ed è particolarmente interessante la sua equivalenza con alcuni degli approcci percezionali citati precedentemente. Inoltre, esso è uno strumento didattico fondamentale nello studio della semantica dei linguaggi di programmazione. Tra coloro che hanno maggiormente contribuito allo sviluppo di questo approccio, nelle sue varie forme, citiamo J. de Bakker, D. Bjœrner, B. Courcelle, M. Gordon, P.D. Mosses, G.D. Plotkin. Esso è stato utilizzato per definire la semantica di importanti linguaggi imperativi (Pascal), funzionali (ML) e concorrenti (Ada).
Semantica algebrica. - Un approccio alla semantica particolarmente adatto a esprimere le proprietà formali dei dati, e che ha avuto un notevole ruolo nell'evoluzione delle metodologie e dei linguaggi di programmazione, è quello denominato semantica algebrica. Esso è sostanzialmente basato sul concetto di tipo astratto di dato. I dati, anziché essere insiemi (come nei linguaggi di programmazione usuali) o insiemi parzialmente ordinati (come nella semantica denotazionale), sono strutture algebriche, cioè insiemi di oggetti dotati di operazioni; in generale si tratta di algebre a più sorti.
Si definisce segnatura Σ una coppia Σ=〈S,F> dove S è un insieme di nomi di insiemi s₁,…,sn (detti sorti di Σ) e F è un insieme di simboli di funzione f₁,…,fm (detti operazioni di Σ) dotati di tipo (corrispondenza tra i simboli in F e l'insieme di stringhe S*→S). Un simbolo di funzione per cui vale tipo(f)=ε→s è detto costante di tipo s. Data una segnatura S, una Σ-algebra è un'interpretazione della segnatura, consiste cioè di una famiglia di insiemi non vuoti As₁,…,Asn (in corrispondenza delle sorti s₁,…,sn di Σ) e una famiglia di funzioni (in corrispondenza delle operazioni f₁,…,fm di Σ).
Esempio. Sia data la segnatura ΣNAT le cui sorti sono: {nat,bool}, le operazioni sono {zero,succ,eq} e il loro tipo è:
zero:→nat; succ:nat→nat; eq:nat,nat→bool.
Associando a nat l'insieme dei naturali e a bool l'insieme {vero, falso} e interpretando le operazioni zero (come la costante 0), succ (come il successore di un naturale), ed eq (come la relazione di uguaglianza tra due interi), si vede che i numeri naturali sono una ΣNAT-algebra.
Il fatto di considerare i dati non come semplici insiemi di valori ma come strutture algebriche ha rappresentato un'importante innovazione nelle teorie e nelle metodologie della programmazione. L'idea, ispirata dal concetto di classe introdotto nel 1970 da O.J. Dahl e K. Nygaard nel linguaggio di programmazione SIMULA (e ripreso in seguito nell'ambito dei linguaggi a oggetti), è stata sviluppata e formalizzata a metà degli anni Settanta per opera di J.V. Guttag, B. Liskov, S.N. Zilles e del gruppo di ricercatori costituito da J.A. Goguen, J.W. Thatcher, E.G. Wagner, J.B. Wright (denominato gruppo ADJ). Essa ha dato luogo, da un lato, allo sviluppo dell'approccio algebrico alla semantica, dall'altro alle metodologie di specifica algebrica del software, basate sul concetto di tipo astratto di dato.
Per definire un tipo astratto di dato è necessario individuare le sorti e le operazioni che lo caratterizzano (cioè la segnatura), nonché le proprietà delle operazioni. Tali proprietà, generalmente espresse in forma di equazioni, caratterizzano la struttura in modo astratto, cioè indipendente dall'implementazione. Perché la struttura sia realizzata correttamente sarà sufficiente che le proprietà fornite nella specifica siano garantite.
Tornando a considerare l'esempio precedente, la specifica dovrà prevedere che l'operazione eq soddisfi le seguenti proprietà:
eq(zero,zero)=vero; eq(x,y)=eq(y,x); eq(zero,succ(x))=
=falso; eq(succ(x),succ(y))=eq(x,y).
Una specifica algebrica consiste in un insieme di tipi astratti di dati, la cui gestione può avvenire solo tramite le operazioni previste nella specifica, in modo che tutti gli aspetti realizzativi siano schermati all'esterno: una concezione modulare non dissimile da quella che caratterizza i moderni linguaggi a oggetti (la cui definizione è stata, in effetti, ampiamente influenzata dalle metodologie di specifica algebrica del software).
La semantica formale dei tipi astratti di dati è formulata mediante il concetto di classe di omomorfismi tra le Σ-algebre che soddisfano le proprietà delle operazioni.
Formalmente, se X è un insieme di nomi di variabili e Σ=〈S,F> è una segnatura, definiamo T(Σ,X) l'insieme dei termini costruiti con le variabili in X e le funzioni in F. Si noti che 〈T(S,X),F> è una Σ-algebra. T(Σ)=T(Σ,∅) è chiamata algebra dei termini di base. Consideriamo l'insieme E di equazioni del tipo t=t′ dove t e t′ sono termini in T(Σ,X). Sia Alg(Σ,E) la famiglia delle Σ-algebre che soddisfano le equazioni in E. Se ≡E è la relazione di equivalenza tra termini indotta dalle equazioni di E e T(Σ)/≡E la partizione in classi indotta su T(Σ) dalla relazione ≡E, definiamo tipo astratto di dato la famiglia di tutte le Σ-algebre isomorfe con T(Σ)/≡E. Si noti che anche 〈T(Σ)/≡E,F> è una Σ-algebra; essa è tale che per ogni algebra A in Alg(Σ,E) esiste un unico omomorfismo 〈T(Σ)/≡E,F> in A. Poiché un'algebra siffatta viene detta iniziale, la semantica dei tipi astratti di dati che abbiamo testé definito viene detta semantica iniziale.
La semantica algebrica e i metodi di specifica algebrica del software hanno avuto negli ultimi anni un notevole sviluppo che ha riguardato vari aspetti (tuttora oggetto di studio) necessari per rendere l'approccio più potente (per es., prevedendo che la specifica utilizzi formule più generali delle equazioni), in grado di esprimere aspetti di programmazione più generali (come la concorrenza), adatto alla specifica formale di sistemi informatici di grandi dimensioni (introducendo meccanismi di specifica gerarchica) e in grado di esprimere la riusabilità del software (mediante il concetto di specifica parametrica). Dal punto di vista dell'evoluzione dei linguaggi di programmazione, oltre al già citato ruolo che il concetto di tipo astratto di dato e altri aspetti di semantica algebrica (polimorfismo, overloading degli operatori ecc.) hanno avuto sullo sviluppo dei linguaggi orientati a oggetti, va segnalato l'impatto dell'approccio algebrico sui linguaggi di specifica. Vari linguaggi di specifica sono stati definiti utilizzando concetti e strutture sviluppati nell'ambito degli studi sulla specifica algebrica del software (CLEAR, OBJ, ACT ONE, ACT TWO, ASL ecc.), e in altri linguaggi, come ML, sono stati aggiunti meccanismi di tipo algebrico per la specifica di tipi di dati e programmi.
Logiche della programmazione e dimostrazione di correttezza. - L'approccio logico allo studio del comportamento dei programmi (v. logica e informatica, App. V) è basato sul principio che un programma sequenziale contenga tutte le informazioni necessarie per determinare il suo comportamento e, pertanto, è possibile definire un sistema deduttivo che consenta di derivare in modo formale, partendo dalla struttura del programma, asserzioni riguardanti le sue proprietà (per es., la terminazione) nonché le proprietà del suo comportamento rispetto allo stato (valore di un insieme di variabili) che esso modifica durante l'esecuzione.
L'esigenza di dimostrare formalmente la correttezza di un programma non era sfuggita a due precursori delle scienze dell'informazione come A.M. Turing e J. von Neumann; tuttavia, solo nella seconda metà degli anni Sessanta sono state proposte adeguate metodologie per opera di R.W. Floyd, P. Naur e, in particolare, di C.A.R. Hoare, che hanno contribuito a porre le basi teoriche dell'i. e a determinare importanti evoluzioni dei linguaggi di programmazione (programmazione strutturata). Nel sistema formale proposto da Hoare (logica di Hoare o semantica assiomatica) viene data particolare enfasi all'analisi della correttezza di un programma rispetto alla specifica delle proprietà che le variabili devono verificare prima e dopo l'esecuzione del programma stesso. Tale logica può essere quindi utilizzata sia come sistema per la verifica a posteriori della correttezza di un programma, sia come metodo di specifica e sviluppo di un programma corretto. Una classica asserzione di correttezza parziale della logica di Hoare si presenta nel seguente modo:
(se prima dell'esecuzione del programma p le variabili soddisfano la proprietà φ, dopo l'esecuzione, se essa termina, esse soddisfano la proprietà ψ). I predicati φ e ψ si chiamano precondizione e postcondizione. Gli assiomi della teoria definiscono il comportamento delle istruzioni elementari di un programma. Per es., l'assioma:
afferma che se prima dell'esecuzione dell'assegnazione vale la proprietà φ in cui ogni occorrenza di x è sostituita dal termine e, dopo l'assegnazione vale la proprietà φ. Nel corso di una dimostrazione di correttezza si propagano le precondizioni e le postcondizioni lungo il programma, sfruttando le regole di inferenza che specificano il comportamento dei costrutti del linguaggio (per es., la regola:
specifica che se per le istruzioni p e q valgono le condizioni φ, ψ, e, rispettivamente, ψ, ξ, per la composizione sequenziale delle due istruzioni valgono le condizioni φ e ξ). In conclusione, se la dimostrazione ha successo, si verificherà che le condizioni sono soddisfatte dall'intero programma.
L'approccio assiomatico alla semantica dei programmi ha portato allo sviluppo di una serie di sistemi formali (logiche della programmazione), per lo più estensioni modali di logiche del prim'ordine. Esempi di tali logiche sono la logica dinamica (Pratt 1976), la logica algoritmica (Salwicki 1977), il calcolo situazionale (Z. Manna, R. Waldinger, 1981), il μ-calcolo (Kozen 1982).
In questi sistemi il linguaggio del prim'ordine viene arricchito introducendo istruzioni e costrutti di un linguaggio di programmazione (per es., composizione sequenziale, iterazione, alternativa in base al valore di verità di un predicato) e uno o più operatori modali che esprimono relazioni tra asserzioni sullo stato del sistema ed esecuzione di programmi. La necessità di utilizzare operatori modali è legata al fatto che mentre nella logica classica si formulano asserzioni in merito a una realtà statica, nel caso delle logiche della programmazione si studia una realtà che evolve dinamicamente durante l'esecuzione di un programma. Una tipica formula modale di questa natura è la seguente:
che appartiene alla logica dinamica ed esprime il fatto che se l'esecuzione del programma p termina, ci si trova in uno stato che soddisfa la proprietà φ. Gli assiomi e le regole di inferenza delle teorie logiche della programmazione contengono, oltre agli assiomi e alle regole di inferenza logiche del prim'ordine, assiomi e regole che stabiliscono relazioni tra programmi e proprietà dello stato. Un tipico esempio, in tal senso, è l'assioma che descrive le proprietà della composizione sequenziale (anch'esso appartenente alla logica dinamica)
Dopo i risultati teorici sviluppati negli anni Settanta e Ottanta, gli anni Novanta hanno visto le prime concrete applicazioni dei metodi formali, basati sugli studi di semantica e logica della programmazione, a casi reali di dimensioni medio-grandi (per es., verifiche di correttezza di microprogrammi per operazioni aritmetiche in processori commerciali). Ciò è avvenuto grazie alla realizzazione di strumenti in grado di effettuare in modo automatico (o semiautomatico) verifiche di correttezza e all'utilizzazione di metodi ibridi capaci di sfruttare le caratteristiche migliori dei diversi sistemi formali.
Semantica di processi concorrenti. - In un reale sistema informatico, l'elaborazione delle informazioni non dà necessariamente luogo a una computazione sequenziale come nei modelli teorici (macchina di Turing, RAM ecc.); al contrario, per vari motivi, nel sistema sono generalmente attive più computazioni (processi). Ciò avviene in diverse circostanze: nei sistemi paralleli o distribuiti, basati cioè su una pluralità di unità di elaborazione (processori) più o meno strettamente interconnesse, che cooperano, comunicando mediante messaggi o mediante unità di memoria condivise, nella risoluzione di un particolare problema o nei sistemi transazionali (casse automatiche, sistemi di prenotazione, sistemi archiviali ecc.), in cui una pluralità di utenti, collegati in rete, accede a una base informativa interrogandola ed eseguendo operazioni che ne modificano il contenuto. Anche nei sistemi monoprocessore e monoutente, la semplice presenza del sistema operativo che interagisce con l'utente per gestire le risorse del sistema dà luogo all'attività simultanea di più processi. Sistemi nei quali siano contemporaneamente presenti più processi vengono detti sistemi concorrenti.
In un sistema concorrente i processi possono interagire tra di loro in modo cooperativo, per il raggiungimento di un obiettivo comune, ma possono anche interagire in modo competitivo contendendosi l'uso delle risorse del sistema e determinando, in caso di errato coordinamento, un'evoluzione scorretta delle singole attività.
Alcuni classici esempi di concorrenza, legati alla necessità di far accedere più processi a risorse condivise, si sono presentati fin dal momento della progettazione dei primi sistemi operativi multiutente. Essi sono stati formulati e analizzati da E. Dijkstra alla fine degli anni Sessanta e pongono tuttora problemi di interesse basilare:
1) aggiornamento del valore di una variabile. Se più processi accedono a una variabile condivisa (si pensi, per es., al saldo di un conto corrente bancario) per leggerne il valore ed eventualmente modificarlo, per garantire la correttezza del sistema è necessario che ogni processo mantenga il controllo della variabile fino a che non ha ultimato l'aggiornamento; è necessario, cioè, che si realizzi la cosiddetta mutua esclusione;
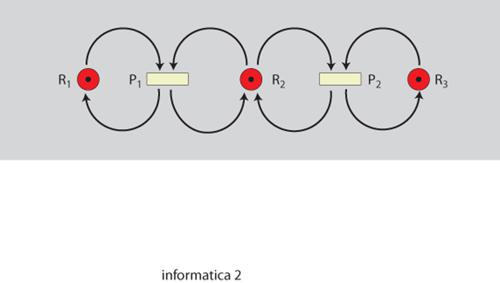
2) condivisione di risorse. Quando più processi necessitano di varie risorse (per es., diverse unità periferiche) per completare il loro compito, si possono verificare situazioni di stallo (nessuno dei processi è in condizione di evolvere perché essi sono reciprocamente in attesa del rilascio di risorse da parte degli altri processi) o di privazione (alcuni processi evolvono ma altri sono permanentemente impossibilitati a procedere), e si devono quindi instaurare opportune politiche di gestione delle risorse stesse che evitino tali inconvenienti;
3) cooperazione tra processi mediante scambio di messaggi. In questo caso siamo in presenza di più processi scrittori e più processi lettori che comunicano lasciando messaggi in una memoria tampone; nel caso che la memoria sia limitata, la correttezza della cooperazione è compromessa se non si fa uso di opportune politiche di gestione.
Per rendere facilmente intuibili i termini del problema della condivisione di risorse, lo studioso olandese E. Dijkstra utilizzò il suggestivo problema dei filosofi a pranzo: cinque filosofi siedono a tavola davanti a un piatto di spaghetti; alla destra di ognuno è disponibile una forchetta. I filosofi alternativamente pensano e mangiano, ma per mangiare hanno bisogno di due forchette (la metafora è legata alla tradizionale difficoltà degli Olandesi nel mangiare gli spaghetti) e devono quindi utilizzare sia quella alla loro destra sia quella alla loro sinistra. Chiaramente ciò dà luogo a una contesa di risorse che dev'essere opportunamente regolamentata per evitare fenomeni di stallo e di privazione.
Molti altri importanti problemi di concorrenza nascono nell'ambito delle basi di dati (per es., per quanto concerne l'esecuzione concorrente di transazioni) e nell'ambito dei sistemi distribuiti e delle reti (per es., il problema della sincronizzazione tra processi, il problema del raggiungimento del consenso circa il valore di una variabile, anche in presenza di alcuni processori inaffidabili, o il problema dell'elezione di un processore che funga da leader tra più processori omogenei). Il problema dei processori inaffidabili è stato chiamato da L. Lamport problema dei generali bizantini, con riferimento alla situazione in cui dei generali bizantini devono concordare l'ora dell'attacco al nemico, anche se tra di essi si annida una minoranza di generali felloni. In tutti questi casi, il problema di garantire il comportamento corretto degli algoritmi è particolarmente complesso e richiede, a sua volta, la correttezza dell'interazione tra processi più elementari. Infine, nel contesto delle reti globali (per es., Internet), complessi problemi di concorrenza nascono dalla mobilità del codice e dal fatto che alcuni dei processi potrebbero intenzionalmente comportarsi in modo ostile.
Rispetto al caso dei sistemi sequenziali, il problema della correttezza del comportamento di sistemi concorrenti è caratterizzato da due fattori: i sistemi concorrenti sono dipendenti dal tempo (il comportamento può essere corretto o scorretto a seconda dell'evoluzione dei processi) e reattivi (in genere sistemi concorrenti, quali un sistema operativo o un sistema di controllo di processi, non hanno un input e un output, ma possono non terminare mai e il loro comportamento è definito in base a come essi interagiscono con l'ambiente). Per questi motivi, per l'analisi e lo studio dei sistemi concorrenti sono stati sviluppati modelli e semantiche diversi e più complessi di quelli utilizzati per i sistemi sequenziali.
Tra i primi modelli definiti per descrivere sistemi concorrenti e sistemi distribuiti sono le reti di Petri (introdotte da A. Petri nel 1962) che, in versioni sempre più sofisticate e ricche di espressività, hanno continuato, con varia fortuna, a essere utilizzate fino a oggi. Nella versione più elementare una rete di Petri è costituita da un insieme finito di posti (che rappresentano condizioni per l'attivazione di processi) e di transizioni (che rappresentano processi) e da archi che li collegano (che rappresentano relazioni di precedenza e/o flussi di risorse). Lo stato di una rete di Petri è caratterizzato dalla presenza di zero, una o più marche (rappresentanti risorse) in corrispondenza dei posti (fig. 2). Poiché un processo consuma risorse quando è attivato e le rilascia al termine, lo scatto di una transizione determina un flusso di risorse e un cambiamento di stato della rete. La fig. 2 rappresenta due processi P₁ e P₂ che vengono eseguiti, non deterministicamente, in mutua esclusione. Se nel posto R₂ fossero disponibili due marche, i processi P₁ e P₂ potrebbero evolvere contemporaneamente.
I modelli formali per descrivere e analizzare sistemi concorrenti si differenziano in base a varie caratteristiche. Innanzitutto, analogamente ai modelli di sistemi sequenziali, essi possono essere di tipo operazionale, cioè orientati a descrivere il sistema in base al suo comportamento interno (modelli intensionali) o di tipo denotazionale, cioè orientati a descrivere il sistema in base al comportamento osservabile dall'esterno (modelli estensionali). Inoltre essi si caratterizzano a seconda del tipo di concorrenza che esprimono: modelli a interposizione (detti, con termine inglese, modelli interleaving), che rappresentano una computazione concorrente come una scelta non deterministica in un insieme di computazioni sequenziali in cui gli eventi si susseguono in tutte le sequenze ammissibili, e modelli di autentica concorrenza, in cui gli eventi sono del tutto asincroni e si svolgono, secondo regole locali di causa ed effetto, in punti diversi del sistema. Le reti di Petri sono un esempio di modello intensionale con autentica concorrenza.
Uno dei primi approcci utilizzati per descrivere sistemi concorrenti e verificarne la correttezza del comportamento è stato proposto da Hoare alla fine degli anni Settanta. Nella sua teoria dei processi sequenziali comunicanti (CSP, Communicating Sequential Processes), che ha ispirato lo sviluppo dei primi linguaggi di programmazione concorrenti (per es., i linguaggi Ada e Occam), Hoare formalizza tre concetti: il parallelismo dei processi, la comunicazione tra processi con appuntamento (rendez-vous), il non determinismo, cui possono essere estesi i metodi di prova sviluppati da Hoare per i linguaggi sequenziali.
Più recentemente i metodi di specifica e verifica di sistemi concorrenti si sono concentrati nelle due direzioni (in un certo senso complementari) delle logiche temporali (introdotte da A. Pnueli sempre alla fine degli anni Settanta) e delle algebre di processi (introdotte da R. Milner nello stesso periodo).
Le logiche temporali sono logiche modali (di tipo proposizionale o predicativo) i cui operatori fondamentali esprimono la validità di un'asserzione p da un certo istante in poi (Gp) o in qualche istante futuro (Fp) o nel prossimo istante (Xp) ovvero la validità di un'asserzione p fino a quando una nuova asserzione q non diventa valida (pUq). Riguardo alla nozione di tempo si può ipotizzare un'unica dimensione temporale su cui tutti gli eventi vengono proiettati (tempo lineare) o situazioni in cui, in alcuni istanti, il tempo si dirama, dando luogo a diverse scale temporali non più confrontabili (tempo ramificato). In quest'ultimo caso la validità di un'asserzione temporale (per es. Gp) potrà verificarsi in tutte le scale temporali future (AGp) o solo in qualche ramo (EGp). L'utilizzazione di logiche temporali ha condotto allo sviluppo di metodi di verifica di correttezza basati su sistemi di dimostrazione o sull'analisi di modelli a stati finiti. Quest'ultimo metodo, nonostante la complessità derivante dalla crescita del numero di stati che può essere esponenziale in funzione del numero di processi presenti nel sistema, si sta rivelando utile, grazie a opportune tecniche, nella realizzazione di strumenti automatici di verifica e nel loro impiego per analizzare la correttezza di sistemi complessi (protocolli di comunicazione a livello hardware e software, sistemi telefonici, sistemi di sicurezza aeroportuali e ferroviari ecc.).
Le algebre di processi sono modelli intensionali nei quali il comportamento di un sistema può essere specificato a diverso livello di astrazione e la correttezza di realizzazione viene espressa come equivalenza operazionale. Il primo approccio algebrico allo studio della concorrenza è stato proposto da R. Milner (1980) con il calcolo di sistemi comunicanti (CCS, Calculus of Communicating Systems), evolutosi poi in una serie di successivi sistemi formali chiamati π-calcolo (ispirato al λ-calcolo) e calcolo delle azioni. Tale approccio assume le stesse nozioni primitive di sincronizzazione e comunicazione mediante scambio di messaggi presenti nei CSP di Hoare ma si caratterizza soprattutto per la rappresentazione di processi mediante espressioni ed equazioni algebriche.
A titolo di esempio mostriamo alcune delle espressioni che possono essere costruite utilizzando gli operatori del linguaggio:
α.E (prefisso): rappresenta il processo che esegue l'azione α e poi si comporta come il processo descritto da E;
ΣiEi (sommatoria): rappresenta un processo che può comportarsi come uno qualsiasi dei processi descritti dalle espressioni Ei;
E₀|E₁ (parallelismo): rappresenta la composizione in parallelo dei due processi descritti da E₀ ed E₁.
Sono inoltre disponibili operatori di punto fisso (ricursione), di ridenominazione di azioni, invio di valori su una porta di uscita e ricezione di valori su una porta di entrata ecc.
La semantica del linguaggio può essere fornita in modo operazionale mediante sistemi di transizioni etichettati (in cui, cioè, le transizioni sono annotate con il nome delle azioni seguite dai processi) o, come si è detto precedentemente, con metodi equazionali.
Un ultimo aspetto relativo alla verifica di sistemi concorrenti riguarda il caso in cui si utilizzino tecniche probabilistiche nella soluzione di problemi di concorrenza, per es. per dirimere contese nell'accesso a risorse (si pensi, per es., a una soluzione probabilistica del problema del pranzo dei filosofi) o per raggiungere più rapidamente il consenso sul valore di una variabile (come nel caso dell'elezione del leader). Un ulteriore esempio che non ammette soluzioni deterministiche e richiede l'adozione di tecniche probabilistiche è quello dell'infrazione della simmetria in una rete di processi identici. Come si può facilmente comprendere, la dimostrazione di correttezza per questo tipo di algoritmi si presenta molto complessa e adeguate logiche modali e probabilistiche sono ancora allo studio.
Gli sviluppi delle tecnologie informatiche lasciano prevedere che i problemi della specifica e della verifica di sistemi concorrenti saranno, in futuro, sempre più centrali nell'ambito delle scienze dell'informazione. Da un lato, infatti, le questioni relative ai sistemi con vincoli temporali stringenti (real time), ai sistemi resistenti, ai malfunzionamenti (fault tolerant), ai sistemi ibridi, in cui sussistono, cioè, componenti digitali e componenti analogiche, richiedono il raffinamento delle metodologie fin qui utilizzate o lo sviluppo di nuovi sistemi formali capaci di rappresentare adeguatamente le realtà di interesse e di consentire efficienti metodi di dimostrazione di correttezza. Dall'altro lato, le applicazioni su rete globale e ad agenti mobili che si stanno diffondendo pongono esigenze di sincronizzazione e comunicazione molto complesse che attualmente i linguaggi a disposizione (Java, Telescript ecc.), dotati di meccanismi di gestione della concorrenza molto rudimentali, non consentono di dominare.
Nuove forme di calcolo
I grandi filoni delle scienze dell'informazione che abbiamo illustrato si sono via via sviluppati avendo come principali punti di riferimento concettuali, da un lato, i primi modelli astratti sviluppati dai logici negli anni Trenta e Quaranta (il modello proposto da Turing, fondato sul concetto di transizione di stato, e quello funzionale sviluppato da A. Church e S.C. Kleene) e, dall'altro, i modelli concretamente realizzati nell'architettura dei calcolatori elettronici, primo fra tutti il modello di von Neumann (che ha direttamente ispirato la macchina a registri), e, successivamente, i vari modelli di architetture distribuite e parallele. Negli anni più recenti, tuttavia, hanno cominciato ad affermarsi, nell'ambito delle scienze dell'informazione, paradigmi di calcolo di notevole interesse, ispirati a meccanismi di elaborazione presenti in vario modo in natura e per tale motivo definiti, a volte, modelli di calcolo naturali (un altro termine con cui ci si riferisce a questi paradigmi di calcolo è soft computing). Rientrano in questa categoria le reti neurali, gli algoritmi genetici, gli elaboratori quantistici e il calcolo biologico o molecolare (v. oltre). L'attenzione rivolta a tali paradigmi, peraltro non tutti di origine recente, è anche da porsi in relazione a sviluppi della tecnologia che hanno permesso (o consentono di ipotizzare) realizzazioni pratiche su di essi basate.
Reti neurali artificiali. - La possibilità di realizzare sistemi di elaborazione capaci di emulare il comportamento del sistema nervoso animale, e in particolare del cervello, ha attratto notevoli energie fin dai primordi dell'informatica. I primi studi di W.S. McCullouch e W. Pitts, e dello stesso von Neumann, volti alla realizzazione di neuroni artificiali risalgono, infatti, al 1943. In un neurone artificiale le quattro componenti fondamentali della struttura neuronale animale (il corpo della cellula, i dendriti, l'assone e le sinapsi) assumono rispettivamente i ruoli, astratti, di: elemento di elaborazione primitivo, canali di ingresso, canale di uscita, interconnessioni.
Secondo questa schematizzazione, quindi, se in ingresso sono presenti i valori (segnali) x₁,…,xn, un neurone artificiale calcola una semplice funzione f(x₁,…,xn). Nelle versioni più elementari la funzione f è, per es., una funzione binaria (soglia) che decide se il valore y=Σiwixi (dove i coefficienti wi sono pesi che vengono attribuiti ai segnali in ingresso xi) supera o meno una certa soglia τ, ovvero una sigmoide, f(y)=1/(1+e⁻cy), che realizza una soglia modulata dal parametro c. Una rete neurale artificiale è costituita da un'interconnessione di neuroni artificiali. La caratteristica fondamentale delle reti neurali come modelli di calcolo è che, in esse, l'informazione non è localizzata in forma simbolica, come in un normale elaboratore, ma è distribuita nei segnali presenti alle interconnessioni fra i diversi neuroni, cioè, intuitivamente, nelle sinapsi. I vari tipi di reti differiscono essenzialmente per il tipo di funzioni realizzate dai neuroni, per la struttura di interconnessione e per le modalità di temporizzazione dei segnali. In particolare, possiamo identificare due tipi fondamentali di reti: quelle di tipo direzionale (feed-forward), chiamate anche sistemi di classificazione, e quelle di tipo bidirezionale (feed-back). Il primo tipo deriva sostanzialmente dal modello introdotto nel 1958 da F. Rosenblatt (chiamato percettrone) e successivamente studiato da M. Minsky e S. Papert alla fine degli anni Sessanta. In una rete direzionale abbiamo che i neuroni sono disposti su livelli (uno di ingresso, uno di uscita e uno o più nascosti) e possono realizzare funzioni di classificazione di oggetti (di grande importanza, per es., nella visione artificiale). In tale modello assume un ruolo fondamentale l'apprendimento che consente (in modo guidato o autonomo) la taratura dei pesi con cui i segnali in ingresso vengono acquisiti ed elaborati dal singolo neurone. Un significativo impulso nell'utilizzazione pratica delle reti neurali è venuto, nel 1985, da D. Rumelhart con l'introduzione del metodo di apprendimento chiamato retropropagazione, un metodo basato su tecniche di minimizzazione dell'errore già utilizzate nel campo del controllo ottimo. Negli stessi anni, per opera di J. Hopfield, si è sviluppata l'altra categoria di reti neurali, le reti bidirezionali. In tali reti (chiamate appunto reti di Hopfield), i segnali si propagano in modo bidirezionale e non sincronizzato tra i neuroni finché la rete non raggiunge uno stato stabile. Poiché tali reti sono affini ai modelli di meccanica statistica (per es. al modello di Ising per il magnetismo) che raggiungono la stabilizzazione ai livelli minimi di energia, esse sono impiegate per risolvere problemi di ottimizzazione (come, per es., il problema del commesso viaggiatore). In tale applicazione, la funzione obiettivo del problema viene utilizzata per definire l'energia del sistema. Per evitare che la rete converga verso ottimi locali di cattiva qualità si utilizzano versioni stocastiche (macchine di Boltzmann) che possono sfuggire agli ottimi locali per giungere a livelli energetici più bassi.
Il motivo per cui le reti neurali hanno avuto un rigoglioso rilancio negli anni Ottanta non è solo legato ai progressi della ricerca modellistica che abbiamo citato ma anche all'evoluzione delle tecnologie hardware che hanno consentito di costruire le prime versioni reali di macchine neurali. Si tratta per lo più di macchine parallele di tipo SIMD (Single Instruction-stream Multiple Data-stream, in cui cioè una singola istruzione opera su molti dati in parallelo) o di tipo sistolico (in cui i dati fluiscono in modo sincrono, analogamente a come il sangue fluisce nelle vene per effetto del battito cardiaco). In considerazione dei positivi risultati conseguiti per la soluzione di specifici compiti (riconoscimento di voce, immagini, scene), la costruzione di macchine neurali è proseguita anche negli anni Novanta. Peraltro, in considerazione del fatto che il principale ostacolo alla realizzazione di circuiti neurali risiede nell'elevato numero di interconnessioni che devono essere previste, si ritiene che le tecnologie ottiche possano essere utilizzate, in futuro, nella realizzazione di reti neurali, meglio delle tecnologie elettroniche.
Algoritmi genetici. - L'idea di adottare un approccio evoluzionistico nella risoluzione di problemi risale anch'essa ai primi decenni dello sviluppo dell'informatica. Diversi autori, tra cui ricordiamo J.H. Holland (1975), hanno considerato, fin dagli anni Sessanta e Settanta, la possibilità di migliorare le prestazioni di un algoritmo (in particolare di un algoritmo di ottimizzazione) adottando un punto di vista genetico. Questo approccio, noto anche come programmazione evolutiva, è stato più recentemente ripreso da D.E. Goldberg e altri nella seconda metà degli anni Ottanta. Esso costituisce sostanzialmente una variante del metodo di ricerca locale, con la differenza che mentre nella ricerca locale si genera una soluzione e si cerca di raggiungere, a partire da essa, la soluzione ottima passando via via a soluzioni localmente migliori, nel caso degli algoritmi genetici si generano popolazioni di soluzioni (distribuite in tutto lo spazio delle soluzioni) le quali, a loro volta, con opportuni metodi di incrocio, generano altre soluzioni; un meccanismo di mutazione e di selezione naturale provvede a far prevalere, nel processo riproduttivo, le soluzioni migliori e a determinare, in definitiva, il successo della specie nella risoluzione del problema dato. Il vantaggio di questo metodo dipende dal fatto che, partendo da una pluralità di soluzioni e operando in modo probabilistico (sia l'incrocio sia le mutazioni sono processi probabilistici), è più difficile che si rimanga intrappolati in ottimi locali. Inoltre è chiaro che il metodo si presta bene a essere implementato in modo efficiente su macchine parallele. Un algoritmo genetico consiste, dunque, in generale, nella ripetizione continua dei tre passi fondamentali: selezione, cioè scelta delle soluzioni (genitori) da incrociare, in base alla loro qualità rispetto alla funzione obiettivo del problema; incrocio, cioè ricombinazione di due soluzioni per generare soluzioni nuove; mutazione, cioè modificazione casuale delle soluzioni ottenute (figli).
Ciascuno dei tre passi può essere realizzato in molti modi e ciò dà luogo a una grande varietà nella tipologia degli algoritmi genetici. Per es., nel meccanismo di selezione si può introdurre il concetto di specie e proibire l'incrocio tra specie diverse (rappresentando così il fatto che certi tipi di incroci possano essere sterili). Per quanto valido in molte applicazioni (in particolare nella risoluzione di problemi inversi, come il disegno dell'ala di un aereo a partire dalla portanza richiesta), l'approccio genetico presenta molti aspetti insoddisfacenti (lentezza della convergenza, fenomeni di deriva genetica ecc.) cui si tenta di ovviare con ulteriori sviluppi della ricerca.
Elaboratori quantistici. - Nonostante la meccanica quantistica sia alla base dei processi che avvengono nei componenti elettronici che costituiscono i calcolatori, essa non ha mai avuto un ruolo nei processi di calcolo che essi eseguono. Recentemente, sulla base di intuizioni di R. Benioff e R.P. Feynman (1986), si è cominciato a studiare il concetto di calcolo quantistico, il suo potere computazionale e le possibilità di una realizzazione fisica. Alla base del modello di calcolo quantistico è il qubit, la versione quantistica del bit. Lo stato di un qubit è espresso dalla sovrapposizione degli stati |0〉 e |1〉, cioè dalla funzione |ψ〉=α|0〉+β|1〉 in cui le ampiezze α e β sono due arbitrari numeri complessi che verificano la condizione α²+β²=1. Per effetto del principio di indeterminazione di Heisenberg, un tentativo di misurare il valore del qubit porta lo stato a collassare sul valore zero o sul valore 1. Un'immediata conseguenza dell'approccio quantistico è, per es., che in particolari circostanze da due qubit si può ricavare una 'quantità di informazioni' superiore al doppio di quella che si ottiene da un singolo qubit. Per analoghi motivi, in un calcolatore quantistico (a differenza di quanto accadrebbe in uno probabilistico, in cui se si intraprende un percorso ciò che sarebbe accaduto seguendo l'altro percorso non produce alcun effetto) più percorsi vengono intrapresi contemporaneamente e il risultato è la sovrapposizione degli stati corrispondenti ai diversi percorsi. In tal modo, due diversi percorsi alternativi possono interferire (in modo costruttivo o distruttivo, esattamente come avviene con le onde luminose), ed è questo effetto che rende potente il calcolo quantistico. Un importante risultato di P.W. Schor (1994) ha recentemente mostrato che, in linea di principio, i calcolatori quantistici potrebbero essere più potenti di quelli deterministici poiché essi consentono di eseguire la fattorizzazione di un intero in tempo polinomiale, cosa che viene ritenuta non possibile con un normale calcolatore. Contemporaneamente sono iniziati gli studi per la realizzazione fisica di calcolatori quantistici (S. Lloyd 1995), un obiettivo certamente stimolante ma la cui fattibilità potrà essere verificata solo nei prossimi anni.
Calcolo molecolare. - È lecito prevedere che, all'inizio del nuovo secolo, grande attenzione verrà anche dedicata al più recente (e sorprendente) dei modelli: il calcolo molecolare. Il paradigma di calcolo chiamato calcolo molecolare (DNA computing o biocomputing) è stato proposto da L. Adleman (1994) e R.J. Lipton (1995). In questo caso non è stata l'evoluzione delle tecnologie elettroniche che ha portato allo sviluppo di questo modello, bensì l'evoluzione delle biotecnologie, in particolare le crescenti capacità acquisite dagli sperimentatori nella manipolazione del materiale genetico, evoluzione che non solo ha ispirato il modello di calcolo astratto ma ne lascia anche prefigurare la possibile realizzazione.
Nel calcolo molecolare, l'informazione è codificata in filamenti di DNA mediante opportune sequenze delle quattro basi fondamentali: adenina, timina, guanina, citosina. I filamenti (corrispondenti quindi a stringhe di caratteri) sono contenuti in provette. Le operazioni che possono essere eseguite sono quelle classiche della manipolazione genetica: per es., individuare e separare dagli altri i filamenti che contengono un particolare carattere in una data posizione, attaccare una sequenza particolare a tutti i filamenti contenuti in una provetta, fondere il contenuto di due provette ecc. Un'operazione di centrifugazione permette inoltre di separare i filamenti anche rispetto al peso. Per realizzare la soluzione di un problema (per es., il problema del commesso viaggiatore) si deve innanzitutto codificare l'istanza del problema con filamenti, poi si eseguono operazioni che trasformano via via i filamenti (generando filamenti che rappresentano tutti i possibili percorsi sul grafo) fino a che un'opportuna fase di filtraggio non consente di estrarre i filamenti che rappresentano soluzioni accettabili (il percorso inizia e termina in una data città e ogni città viene visitata una e una sola volta) e la centrifugazione permette di selezionare le soluzioni migliori (più leggere). Si noti che il modello è intrinsecamente parallelo e non deterministico. Le misure di complessità connaturate con esso sono il numero di operazioni di manipolazione eseguite (tempo) e il numero totale di filamenti utilizzati (spazio). Anche se, nel caso di problemi NP-completi, l'esplosione esponenziale dello spazio delle soluzioni non viene eliminata, la dimensione estremamente piccola della rappresentazione delle informazioni permette di considerare fattibile la generazione di un numero elevatissimo di soluzioni (per es. 2⁷⁰) e quindi di poter risolvere praticamente problemi anche molto complessi.
bibliografia
L.R. Ford, D.R. Fulkerson, Maximal flow through a network, in Canadian journal of mathematics, 1956, 8, pp. 399-404.
J.M. Cooley, J.W. Tukey, An algorithm for the machine calculation of complex Fourier series, in Mathematics of computation, 1965, 19, pp. 297-301.
D.E. Knuth, The art of computer programming, 1° vol. Fundamental algorithms, 2° vol. Seminumerical algorithms, 3° vol. Sorting and searching, Reading (Mass.), 1968-73.
V. Strassen, Gaussian elimination is not optimal, in Numerische Mathematik, 1969, 13, pp. 354-56.
J.H. Holland, Adaptation in natural and artificial systems, Ann Arbor (Mich.) 1975.
V.R. Pratt, Semantical considerations on Floyd-Haare logic, in Proceedings of the 17th IEEE symposium on foundations of computer science, 1976, pp. 109-21.
A. Salwicki, Algorithmic logic: a tool for investigations of programs, in Logics, foundations of mathematics, and computability theory, ed. R.E. Butts, K.J.J. Hintikka, Dordrecht-Boston 1977³, pp. 281-95.
M.R. Garey, D.S. Johnson, Computers and intractability. A guide to the theory of NP-completeness, San Francisco (Calif.) 1979.
M.J.C. Gordon, The denotational description of programming languages. An introduction, New York 1979.
D. Harel, First-order dynamic logic, Berlin-New York 1979.
R. Milner, A calculus of communicating systems, Berlin-New York 1980.
D. Kazen, Results on the propositional μ-calculus, in Automata, languages, and programming. 9th colloquium, Aarhus (Denmark), july 12-16, 1982, ed. M. Nielsen, E.M. Schmidt, Berlin-New York 1982, pp. 348-59.
H.P. Barendregt, The lambda calculus, its syntax and semantics, Amsterdam-New York 1984.
E.C.R. Hehner, The logic of programming, Englewood Cliffs (N.J.) 1984.
G. Ausiello, A. Marchetti Spaccamela, M. Protasi, Teoria e progetto di algoritmi fondamentali, Milano 1985.
H. Ehrig, B. Mahr, Fundamentals of algebraic specifications, EATCS monographs on theoretical computer science, 2 voll., Berlin-New York 1985.
C.A.R. Hoare, Communicating sequential processes, Englewood Cliffs (N.J.) 1985.
R.P. Feynman, Quantum mechanical computers, in Foundations of physics, 1986, pp. 507-31.
A.V. Goldberg, R.E. Tarjan, A new approach to the maximum flow problem, in Proceedings of the 18th annual ACM symposium on theory of computing, 1986, pp. 136-46.
D. Coppersmith, S. Winograd, Matrix multiplication via arithmetic progression, in Proceedings of the 19th annual ACM symposium on theory of computing, 1987, pp. 1-6.
D. Harel, Algorithmics. The spirit of computing, Wokingham-Reading (Mass.) 1987.
R.S. Boyer, J.S. Moore, A computational logic handbook, Boston 1988.
D.E. Goldberg, Genetic algorithms in search, optimization and machine learning, Reading (Mass.) 1989.
R. Milner, Communication and concurrency, New York 1989.
Handbook of theoretical computer science, vol. A, Algorithms and complexity, e vol. B, Formal models and semantics, ed. J. Van Leeuwen, 2 voll., Amsterdam-New York-Cambridge (Mass.) 1990.
D.P. Bovet, P.L. Crescenzi, Teoria della complessità computazionale, Milano 1991.
Modelli e linguaggi dell'informatica, a cura di T. De Mauro, Milano 1991.
Software engineer's reference book, ed. J.A. McDermid, Oxford-Boston 1991.
Z. Manna, A. Pnueli, The temporal logic of reactive and concurrent systems, New York 1992.
Modern heuristic techniques for combinatorial problems, ed. C.R. Reeves, New York 1993.
L. Adleman, Molecular computation of solutions to combinatorial problems, in Science, 1994, 266, pp. 1021-24.
P.W. Schor, Algorithms for quantum computation: discrete logarithm and factoring, in Proceedings of the 35th annual IEEE symposium on foundations of computer science, 1994, pp. 124-28.
G. Tel, Introduction to distributed algorithms, New York-Cambridge 1994.
Computer science today. Recent trends and developments, ed. J. van Leeuwen, Berlin-New York 1995.
R.J. Lipton, DNA solutions to hard computational problems, in Science, 1995, 262, pp. 542-45.
S. Lloyd, Quantum-mechanical computers, in Scientific American, 1995, 273, 4, pp. 140-45.
R. Motwani, P. Raghavan, Randomized algorithms, Cambridge-New York 1995.
D.E. Shasha, C. Lazere, Out of their minds. The lives and discoveries of 15 great computer scientists, New York 1995.
R. Rojas, Neural networks. A systematic introduction, Berlin-New York 1996.
Strategic directions in computing research, in ACM Computing surveys (ACM 50th Anniversary Issue), 1996, 4.
Approximation algorithms for NP-hard problems, ed. D.S. Hochbaum, Boston 1997.
Online algorithms, ed. A. Fiat, G.J. Woeginger, Berlin-New York 1998.
Tecnologie dell'informazione
di Carlo Batini
Le tecnologie dell'informazione hanno presentato negli anni Novanta, e continuano a presentare, un'evoluzione rapidissima. Sono peraltro straordinariamente pervasive, poiché forniscono strumenti e metodi per rappresentare, manipolare, ritrovare, elaborare quella sofisticata fonte di intelligenza, di emozioni, di potere, di comunicazione, di comprensione della realtà costituita dall'informazione. Data la vastità del tema, vengono di seguito analizzati nelle loro linee evolutive 'paradigmi tecnologici' piuttosto che tecnologie specifiche, privilegiando le tecnologie di maggiore impatto e diffusione nelle attività produttive e nella vita individuale rispetto alle tecnologie di ricerca.
Le tecnologie dell'informazione sono utilizzate per elaborare, ritrovare, scambiare informazioni. Il termine informazione ha così vaste sfumature che assumeremo per esso un significato intuitivo, solo esemplificato. È informazione quella che cerchiamo in un orario ferroviario, in una statistica per prendere una decisone di politica pubblica, che riportiamo in un modello per la dichiarazione dei redditi, che cerchiamo sul viso del medico quando ci comunica i risultati delle analisi. Intuitivamente, i primi tre tipi di informazioni citati sono rappresentabili in uno strumento automatico, mentre il quarto no.
L'evoluzione delle tecnologie dell'informazione è caratterizzata da almeno tre generazioni, che spesso nello svilupparsi delle organizzazioni all'interno delle quali vengono impiegate (un ufficio della pubblica amministrazione, un'azienda, una banca, ma anche un nucleo familiare ecc.), si sono temporalmente sovrapposte: la generazione dei grandi elaboratori (mainframe) e dei sistemi transazionali. In questi sistemi un unico elaboratore, con un'elevata potenza di calcolo e dotato di rilevanti apparecchiature periferiche (per es., stampanti) e infrastrutture di comunicazione, è collegato a un vasto insieme di terminali remoti, da ciascuno dei quali è possibile inviare richieste di elaborazione usualmente semplici e predefinite, chiamate transazioni (per es., "aggiorna l'archivio delle prenotazioni per un particolare volo aereo"). In questi sistemi vi è dunque un unico componente che effettua le elaborazioni, più un ampio insieme di terminali per immettere i dati e ricevere i risultati. È scarsa o nulla la possibilità per l'utente del sistema di effettuare elaborazioni per il proprio lavoro personale, ovvero non inizialmente previste, e in ogni caso esse devono utilizzare l'elaboratore centrale. In questo caso il sistema informativo è utilizzato prevalentemente come tecnologia per migliorare la produzione, rappresenta un sistema fortemente gerarchico e si modella sulla struttura organizzativa, caratterizzata da un elevato numero di livelli funzionali, secondo la forma classica della piramide aziendale. In tale situazione, i processi 'operativi' sono quelli di prevalente oggetto dell'automazione; la generazione dei personal computer e dell'i. individuale, caratterizzata da un sempre più ampio utilizzo di elaboratori di potenza più ridotta dei mainframe, con interfacce utente più evolute e allo stesso tempo più semplici, su cui viene svolta dall'utente, in modo autonomo, parte della propria attività lavorativa. I personal computer sono utilizzati, oltre che per attività lavorativa, per esigenze legate alla propria vita privata, al divertimento, alla formazione. Nel caso di utilizzo in un'organizzazione, questa cambia usualmente aspetto, riducendo il numero dei livelli gerarchici e distribuendo ai livelli operativi funzioni prevalentemente svolte dai livelli alti; la generazione delle reti cooperative e del lavoro di gruppo, in cui l'insieme degli elaboratori è collegato a una rete di comunicazione e può accedere a servizi condivisi, come banche dati o posta elettronica. In questo caso, viene enfatizzato il ruolo dell'i. come tecnologia di intermediazione ed è quindi esaltato il ruolo di cooperazione che la tecnologia informatica può svolgere, riducendo le barriere burocratiche e favorendo la comunicazione e la trasparenza.
Si è visto che gli utenti dei sistemi di elaborazione possono utilizzarli per esigenze personali, ovvero perché inseriti in un'organizzazione. In entrambi i casi, possono operare su un sistema di calcolo autonomo o in un sistema connesso in rete con altri sistemi. Si parla perciò di un sistema informativo quando si vuole intendere un insieme di risorse umane, di calcolo, di comunicazione che ha lo scopo di acquisire, memorizzare, elaborare, ritrovare, scambiare, produrre le informazioni necessarie a un'organizzazione per il suo funzionamento. Per sistema di calcolo si intende invece la parte del sistema informativo costituita dalle tecnologie informatiche per l'acquisizione e l'elaborazione automatica dell'informazione. Il sistema di comunicazione è infine l'insieme delle tecnologie che permettono la trasmissione dell'informazione tra sorgenti e destinazioni distanti. Negli anni Novanta le tecnologie sviluppate per i sistemi di calcolo e per i sistemi di comunicazione sono talmente integrate tra loro che si usa parlare di 'tecnologie dell'informazione e della comunicazione'.
Un sistema di calcolo è usualmente composto di diverse parti che interagiscono tra loro per produrre le elaborazioni richieste dagli utenti. L'hardware (cioè i circuiti integrati e i componenti elettrici e meccanici) è usualmente utilizzato per l'unità di elaborazione, responsabile dell'esecuzione delle istruzioni elementari interpretabili dal sistema (spesso chiamata CPU, Central Processing Unit); per le unità periferiche o di ingresso/uscita, cioè le risorse utilizzate per acquisire le informazioni in ingresso al sistema di calcolo e restituire i risultati (per es. stampanti, video, tastiera, scanner); per le unità di memorizzazione, in cui vengono permanentemente conservate le informazioni che è necessario ritrovare nel tempo (per es. nastri, dischi, CD-ROM); per i circuiti e canali che collegano le varie unità e permettono di scambiare tra loro informazioni.
Il software, cioè i programmi, costituiti da insiemi di istruzioni interpretabili ed eseguibili dalle unità menzionate, permette di arricchire il sistema di calcolo con funzioni di elaborazione la cui potenza ha come limite il computabile.
Si distingue usualmente: a) il software applicativo, costituito dai programmi sviluppati per esigenze specifiche di particolari utenti o categorie di utenti. Per es., programmi per ordinare un insieme di nomi, per la contabilità, per la produzione, per la prenotazione di posti aerei, per un gioco elettronico. Il software applicativo può essere realizzato per esigenze specifiche (per es., un programma per l'elaborazione delle dichiarazioni dei redditi), ovvero tramite pacchetti applicativi o soluzioni parametriche, per essere riutilizzato o venduto a una pluralità di utenti (per es., un programma per la gestione del personale, o un gioco elettronico); b) il software di ambiente, costituito da programmi che possono diventare di frequente utilizzo per realizzare il software applicativo, e che perciò offrono funzionalità specifiche per risolvere classi di problemi: è un esempio di questo tipo di software un sistema di gestione di basi di dati (v. oltre: Le tecnologie per i sistemi distribuiti), che permette di realizzare software applicativo che richiede di accedere a un insieme di archivi; c) il software di base, che permette all'insieme dei programmi delle precedenti categorie di utilizzare in modo efficiente le risorse di cui si compone il sistema di calcolo. Il sistema operativo è il più significativo esempio di software di base, e una sua tipica funzionalità è quella di disciplinare l'utilizzo dell'unità di elaborazione da parte dei programmi (software applicativo e di ambiente) che operano nel sistema di calcolo.
Modalità di impiego delle tecnologie informatiche
Un'importante tematica sviluppatasi negli ultimi anni riguarda l'analisi delle modalità con cui le tecnologie dell'informazione possono essere utilizzate nelle organizzazioni per il miglioramento delle proprie attività, e quindi il rapporto tra sistema di calcolo, sistema informativo e sistema di comunicazione. Anche in questo caso, non sempre è possibile analizzare separatamente i tre sistemi. Tuttavia, tra le tecnologie dell'informazione che si sono evolute in modo significativo nel corso del tempo, si sono affermate: le tecnologie per l'informatica individuale, che comprendono i personal computer, le periferiche connesse, i pacchetti applicativi, sviluppati per semplificare e migliorare le attività di singole persone. I temi relativi all'evoluzione delle interfacce utente, che tanta parte hanno avuto per rendere accessibili i sistemi di calcolo a utenti con culture, lingue, evoluzione psicofisica differenti, assumono qui un peso rilevante; le tecnologie per i sistemi informativi in rete o distribuiti, negli aspetti relativi al software di base, di ambiente e software applicativo, nell'ambito delle quali, attraverso sforzi eccezionali, sono stati ottenuti risultati importanti per raggiungere l'obiettivo di far cooperare e interoperare utenti e programmi applicativi sviluppati in passato nell'informatica; la multimedialità, intesa come l'insieme di tecnologie per la rappresentazione ed elaborazione di informazioni che superano le forme tradizionali, come disegni, mappe, immagini fisse o in movimento, suoni.
Non saranno invece affrontati importanti aspetti che pure in un'interpretazione estensiva ricadono in parte nella tecnologia dell'informazione, quali: le architetture dei sistemi di calcolo, le applicazioni dell'i. teorica, l'intelligenza artificiale e la rappresentazione della conoscenza, l'ingegneria del software, le tecnologie della comunicazione.
L'evoluzione delle tecnologie per l'informatica individuale
Nell'elaborazione personale, un sistema di calcolo è utilizzato come strumento per il lavoro individuale. Tra le funzioni tipiche del lavoro individuale vi sono: l'elaborazione di testi, per comporre un testo, definire un formato, scegliere il tipo e la dimensione del carattere ecc.; i fogli elettronici, per comporre calcoli di varia natura su un foglio virtuale a n dimensioni; la creazione di presentazioni, costituita da sequenze di fogli in cui è possibile comporre testi, tabelle, disegni, suoni; l'agenda e il calendario elettronico, per organizzare appuntamenti e pianificare attività; l'elaborazione di disegni, in cui l'elaboratore fornisce direttamente le figure base per la produzione del disegno, ed esegue varie funzioni di manipolazione delle immagini quali la rotazione, la riduzione ecc.; l'elaborazione di pubblicazioni, in cui si hanno a disposizione funzioni per generare pubblicazioni con formato professionale; l'organizzazione in un insieme di archivi e cartelle virtuali di tutti i documenti generati e memorizzati elettronicamente, simulando in questo modo l'usuale gestione manuale della carta.
Oltre alle precedenti funzioni, usualmente denominate di automazione d'ufficio, l'utilizzo dei sistemi di calcolo nell'elaborazione personale si è diffuso anche in un insieme di attività che, pur essendo più specifiche delle precedenti, coinvolgono vaste e diversificate aree di utenti. Citiamo la progettazione aiutata dal calcolatore, in cui l'elaboratore fornisce un insieme di strumenti per il disegno architettonico e industriale che vanno dalla disponibilità di componenti di base alla produzione di viste e prospettive, e la gestione di progetto in cui l'elaboratore fornisce strumenti per l'aiuto alla pianificazione, l'analisi dei costi, la gestione del personale coinvolto, l'individuazione di attività critiche al fine di ottimizzare tempi, risorse e costi.
Nel tempo, gli strumenti per l'i. individuale si sono arricchiti di diverse caratteristiche che li hanno resi adatti a una platea sempre più vasta di utenti, quali la diversificazione delle tecnologie in elaboratori da tavolo (desktop personal computer) ed elaboratori portatili.
Particolare importanza nelle tecnologie per calcolatori personali ha avuto lo sviluppo dell'interfaccia utente, intesa come l'insieme degli strumenti e funzionalità a disposizione dell'utente per esprimere le proprie esigenze e recepire i risultati dell'elaborazione. A questo proposito, sono stati e sono tuttora di cruciale importanza i contributi che scienze come l'ergonomia hanno fornito alla progettazione dei calcolatori. Considerazioni di tipo ergonomico hanno infatti prodotto un'ottimale disposizione dei comandi del calcolatore, che sia funzionale (video e tasti sono posizionati in modo che quelli funzionalmente collegati sono anche spazialmente vicini), sequenziale (la posizione dei comandi deve riflettere la tipica sequenza di utilizzo di un utente), ottimizzata rispetto alla frequenza di accesso (i comandi usati più di frequente sono i più facilmente raggiungibili). In questa ricerca di ottimizzazione nel processo di comunicazione tra utente ed elaboratore, è stato determinato anche l'uso contemporaneo di un limitato numero di colori e la scelta di alcuni colori invece che altri.
Data la grande importanza rivestita dal problema della comunicazione tra uomo e macchina, lo studio di modalità di interazione più amichevoli (user friendly) nei riguardi dell'utente finale è uno dei campi in cui più forte è stato lo sviluppo delle tecnologie informatiche.
La modalità classica di interazione negli anni Ottanta era tramite comandi. Questa scelta aveva l'unico vantaggio di offrire un accesso diretto alle funzionalità del sistema, ma anche numerosi svantaggi, di cui il più evidente è la necessità di ricordare i nomi e le modalità di utilizzo dei comandi, e altri più sostanziali si riferiscono allo stile dell'interazione. Infatti l'utente non può iniziare più attività contemporaneamente, ma è forzato a concentrarsi su un unico compito; l'elaboratore non mostra in alcun modo il contesto in cui l'utente sta operando e non c'è una reazione immediatamente percepibile a fronte dei comandi dell'utente; è molto difficile, e spesso impossibile, cancellare l'effetto di un comando errato.
Le interfacce WIMP. - Queste e altre considerazioni hanno portato allo sviluppo di una nuova modalità di interazione, completamente rivoluzionaria rispetto alle interfacce 'a comandi', in cui l'elaboratore si avvicina all'utente e non viceversa. Tale modalità è implementata nelle cosiddette WIMP interfaces (spesso fatte coincidere con le Graphical UserInterfaces, GUIs), cioè interfacce basate su: Windows (finestre), Icons (icone), Menus (menu) e Pointers (dispositivi di selezione basati sul puntamento, come per es., il mouse). Due altri aspetti cruciali di queste interfacce riguardano l'utilizzo di metafore (simboli o concetti che rimandano ad altri concetti) e della manipolazione diretta (la possibilità di fare direttamente riferimento alla funzione od oggetto di interesse).
La combinazione di queste diverse componenti permette di realizzare un dialogo migliore tra utente e sistema. In particolare: la disponibilità sullo schermo di più finestre contemporaneamente, ognuna delle quali può essere usata per svolgere un'attività diversa, riflette l'abilità umana di pensare e svolgere più compiti simultanei; i menu contengono, raggruppati logicamente e funzionalmente, i vari comandi e opzioni a disposizione dell'utente, che possono essere semplicemente selezionati, eliminando così la necessità di ricordarne i nomi; i dispositivi di puntamento (per es., il mouse) sono essenziali nella realizzazione del paradigma di manipolazione diretta, dove l'utente ha l'impressione di agire fisicamente sugli oggetti mostrati sullo schermo. I principi base di questo paradigma sono: visibilità degli oggetti di interesse; sostituzione dei comandi testuali con la manipolazione degli oggetti mostrati sullo schermo; reazione immediata e percettibile del sistema a ogni azione dell'utente; disponibilità di comandi di ritorno a uno stato precedente, che garantisce l'utente sulla non definitività delle scelte e lo rende psicologicamente disponibile all'esplorazione degli strumenti; correttezza sintattica garantita di tutte le azioni di manipolazione dell'utente, così da eliminare la possibilità di errori casuali nella formulazione di un comando; le icone, cioè rappresentazioni stilizzate di figure, e altri formalismi grafici, quali i diagrammi e le tabelle, sono indispensabili per rappresentare gli oggetti da manipolare sullo schermo. Tale rappresentazione può essere una semplice riproduzione dell'oggetto, nel caso di oggetti concreti, oppure un'immagine più stilizzata e simbolica, nel caso di oggetti sia astratti sia concreti. In quest'ultimo caso, l'immagine dell'oggetto viene utilizzata in senso metaforico per evocare l'oggetto stesso. Per es., un concetto astratto come la fragilità viene rappresentato tramite un bicchiere rotto, la disponibilità di cure mediche con una croce rossa ecc.; la metafora, in generale, viene utilizzata non soltanto per visualizzare alcuni concetti, ma essenzialmente per creare un ambiente interattivo più confortevole per l'utente, sfruttando la conoscenza che questi già possiede in altri domini. Per es., i sistemi il cui scopo è fornire un ambiente per stazioni di lavoro personali, utilizzano la metafora della 'scrivania', sfruttando la familiarità degli utilizzatori con l'organizzazione di un ufficio e con le corrispondenti procedure di lavoro. In altri casi, il meccanismo di selezione diretta è utilizzabile anche come meccanismo per esprimere un comando: per es., il comando di 'gettare' un archivio nel cestino può essere effettuato direttamente spostando l'icona nel cestino. L'esempio del cestino mostra anche uno dei limiti della metafora, cioè l'impossibilità di far coincidere tutte le caratteristiche dell'oggetto evocato con quelle dell'oggetto usato per evocarlo. Infatti, è noto che in alcuni sistemi il cestino, nella metafora della scrivania, è usato anche per estrarre i dischetti dal calcolatore. È evidente come un singolo oggetto possa essere sovraccaricato di significati e, d'altra parte, come non ci sia nulla di intuitivo o familiare nel gettare via qualche cosa che non si vuole distruggere ma riutilizzare.
Strettamente correlato con lo stile di interazione descritto è il paradigma 'ciò che vedi è ciò che ottieni', in cui la differenza tra la rappresentazione visuale e l'oggetto reale che si ottiene a fronte di un'elaborazione è minima, se non nulla. Purtroppo, l'immediatezza di questo paradigma implica una forte limitazione: non si può ottenere niente di più sofisticato di ciò che si può visualizzare direttamente, così come non è possibile eseguire comandi che non siano esprimibili in termini di manipolazione diretta.
Il foglio elettronico. - Nell'ambito delle tecnologie per l'i. individuale, lo strumento più diffuso e popolare è il foglio elettronico, da molti considerato, forse ancor più che l'elaborazione di testi, l'applicazione più sofisticata e potente; è stato anche chiamato la killer application (applicazione assassina), nel senso che è spesso l'applicazione che spinge molti a dotarsi di un elaboratore personale.
In linea di principio, un foglio elettronico è un insieme di una o più griglie bidimensionali su cui è possibile rappresentare vari insiemi di dati, elaborazioni su tali dati e diagrammi che mostrano in forma grafica tali elaborazioni. Le funzioni disponibili sono matematiche, finanziarie, statistiche, logiche, di selezione di dati che rispettano determinate condizioni. Nell'esempio riportato in fig. 5, la riga totale riporta colonna per colonna le somme dei valori delle righe precedenti, e la colonna medie riporta le medie dei valori delle righe adiacenti. Il grafico a istogramma tridimensionale rappresenta i dati di base della sezione interna. Tutte le precedenti elaborazioni sono effettuabili con semplici comandi di selezione, e sono guidate dal sistema che, per es., nel caso della generazione del grafico, chiede di segnalare l'area da rappresentare (selezionata con il mouse), il tipo di grafico tra un vasto insieme di possibili forme, l'eventuale titolo ecc.
L'altra caratteristica che rende potente l'uso delle applicazioni citate è la loro elevata interoperabilità, intesa come possibilità di invocare da ognuna delle applicazioni funzionalità offerte dalle altre (per es., inserire in un testo un foglio elettronico, per cui il successivo aggiornamento del foglio elettronico porta a un automatico aggiornamento del documento) e possibilità di importare ed esportare dati tra le varie applicazioni (per cui, per es., una tabella inizialmente composta con un elaboratore di testi può essere trasformata in un foglio elettronico), scegliendo in questo modo ogni volta l'ambiente più adatto per effettuare elaborazioni e manipolazioni di dati.
Le tecnologie per i sistemi distribuiti
Nell'elaborazione distribuita, gli utenti hanno la possibilità di comunicare e di scambiare informazioni e programmi elaborativi, e dunque di condurre insieme attività lavorative. In questo caso, gli utenti usano elaboratori personali, e una rete di comunicazione per collegarsi con altre risorse di elaborazione. I sistemi distribuiti hanno subito una grande espansione grazie allo sviluppo delle reti locali, che collegano gruppi di elaboratori personali collocati in un edificio, e delle reti geografiche, che collegano elaboratori situati in vaste aree geografiche in tutto il mondo.
In un sistema distribuito, acquista grande importanza un nuovo componente del software di base e di sistema, chiamato software per la gestione delle comunicazioni, che coordina il trasferimento delle funzioni elaborative e delle informazioni tra i vari nodi della rete, garantendo le proprietà di efficienza (il trasferimento deve avvenire in tempo ragionevole e con ridotto uso di risorse elaborative), correttezza (a conclusione dell'operazione, l'esito dev'essere esattamente quello previsto dall'operazione), affidabilità (anche in presenza di malfunzionamenti l'operazione deve concludersi), sicurezza (non vi devono essere intrusioni, l'operazione dev'essere visibile e avere effetti sui soli soggetti coinvolti inizialmente).
Si può comprendere come la struttura di un sistema distribuito sia molto più complessa di quella di un sistema tradizionale, in cui la gestione centralizzata garantisce uniformità di comportamento e semplicità di gestione. Nei primi sistemi con gestione distribuita, le aziende produttrici di software hanno realizzato sistemi caratterizzati da soluzioni tipicamente proprietarie, cioè proprie di un'azienda e non compatibili con quelle di altre aziende. C'era quindi la necessità di adottare per una rete soluzioni tutte proprietarie, ma omogenee al loro interno. Ciò garantiva, all'interno di ogni singola rete, la possibilità di usare i servizi offerti dalla distribuzione, ma impediva un'autentica interoperabilità tra reti che avessero anche un componente non omogeneo.
Un secondo problema, ancora più critico del precedente, per il quale l'evoluzione delle architetture distribuite ha dovuto trovare (e sta tuttora trovando) soluzioni tecnologiche, è quello della frammentazione dei dati e delle funzioni che caratterizza le attività di utenti che operano in una stessa organizzazione. Anche indipendentemente dall'uso delle tecnologie dell'informazione, noi percepiamo comunemente che le informazioni utilizzate in un'organizzazione sono sparse in una miriade di archivi, e che i processi di lavoro (cioè le attività che producono, svolte tutte insieme, un risultato per l'organizzazione, per es. una politica di intervento per una pubblica amministrazione ovvero un prodotto da vendere sul mercato per un'azienda manifatturiera) sono frammentati in tante attività elementari svolte da diverse funzioni organizzative. Relativamente al significato delle informazioni rappresentate negli archivi, e delle funzioni elaborative disponibili nei sistemi, tale frammentazione porta, al di là dell'eterogeneità tecnologica segnalata in precedenza, un'eterogeneità semantica, cioè legata al significato delle informazioni, che è intrinseca alle architetture distribuite.
Un terzo problema, che si pone via via che vengono fornite soluzioni tecnologiche ai precedenti problemi in termini di nuovi prodotti, è quello di fare i conti con l'eredità del passato (i cosiddetti legacy systems, sistemi ereditati), cioè con sistemi la cui realizzazione, in termini di tempi e costi, ha coinvolto ingenti risorse organizzative e ha portato all'automazione di importanti processi di lavoro, che non possono essere dismessi, e, come tali, creano un'implicita, forte resistenza al cambiamento.
Le principali tecnologie dell'informazione per i sistemi distribuiti, che possono in qualche misura portare a soluzione i precedenti problemi, sono: le tecnologie per la cooperazione tra dati; le tecnologie per la cooperazione tra applicazioni; i sistemi per il lavoro di gruppo; la rete Internet e i servizi collegati.
Una base di dati (BD) è un insieme di archivi condivisi da una pluralità di utenti in modo efficiente, affidabile e corretto. Esistono anche basi di dati accessibili da singoli utenti per elaborazioni personali (in questo caso, la funzione ricade tra quelle per l'i. individuale), ma è proprio insito nel concetto di base di dati il fatto che i dati siano messi in comune, siano integrati tra di loro, per poter essere utilizzati da un vasto insieme di utenti attuali e potenziali. In questo senso, una base di dati porta a superare la gestione tipica degli archivi che nel passato era locale alle singole applicazioni informatiche, e dunque a singoli utenti o piccoli gruppi di utenti.
Una base di dati ha perciò un significato organizzativo prima ancora che tecnologico, e nelle sue prime realizzazioni era caratterizzata da forte impulso alla centralizzazione logica e fisica dei dati in un unico strumento di elaborazione. Un sistema di gestione di dati (o Data Base Management System, DBMS) è un insieme di programmi software che garantiscono, nell'accesso alla base di dati, le proprietà precedentemente enunciate. Una tipica funzione offerta da un DBHS è costituita da un linguaggio di interrogazione, che permette agli utenti di formulare richieste alla base di dati.
La forma più stretta di cooperazione tra basi di dati si ottiene mediante la loro integrazione in un'unica base dati, procedura che corrisponde al ritorno alla precedente situazione di totale centralizzazione. Questa soluzione ha certamente il vantaggio di portare a un'integrazione anche di natura semantica tra le diverse basi di dati, e facilita perciò la comprensione tra gli utenti e la correttezza delle elaborazioni. Per fare un esempio, se nelle attuali basi di dati compaiono due archivi, in uno dei quali sono riportati in distinte tabelle i fatturati di un insieme di aziende nei dodici distinti mesi dell'anno, espressi in migliaia di lire, e nell'altro tale insieme di informazioni è rappresentato in un'unica tabella, con i fatturati espressi in milioni, nella base dati integrata tali differenze di rappresentazione vengono rimosse, dando luogo a un'unica omogenea rappresentazione. Questa forma di integrazione è in realtà molto difficile da attuare, per la grande rapidità con cui dati e basi di dati evolvono nelle organizzazioni, e spesso è inopportuna o non realizzabile, per l'autonomia che utenti e gruppi di utenti intendono mantenere sulle basi di dati da essi create e aggiornate.
Una variante della precedente scelta è quella delle basi di dati distribuite, in cui la base dati è ancora gestita da un unico DBMS, ma può essere frammentata in tante basi di dati locali. Ciò in genere migliora l'efficienza per accessi locali, ma rende più complessi i problemi di aggiornamento su diverse basi di dati. In questa soluzione, usualmente, continua a sussistere un'integrazione forte tra le basi di dati locali, che adottano un'unica rappresentazione delle informazioni.
Tutte le soluzioni successivamente esposte indeboliscono progressivamente il legame tra le diverse basi di dati del sistema cooperativo. In una base di dati federata ad accoppiamento forte le diverse basi di dati vengono gestite autonomamente da diversi DBMS, ma esiste un nuovo componente software che ha la possibilità di accedere omogeneamente alle diverse basi di dati, coordinandone le operazioni. In una base di dati federata ad accoppiamento debole, rispetto alla precedente, il nuovo componente garantisce soltanto una visione virtuale integrata, ma non ha potere di intervento gestionale sui sistemi che rimangono fortemente autonomi.
Le tecnologie a gateway (traduttori o filtri tecnologici) permettono di tradurre richieste formulate in un linguaggio per un DBMS a, in termini di richieste per il linguaggio adottato dal DBMS b. Hanno il vantaggio che non richiedono alcuno sviluppo di software aggiuntivo, o ne richiedono uno limitato, ma necessitano di componenti ad hoc per ogni singola relazione tra sistemi distinti, e fanno perdere la trasparenza resa possibile dalle soluzioni precedenti. Il meccanismo più debole di cooperazione tra basi di dati è quello dell'estrazione e trasferimento di dati, con aggiornamento periodico della base dati locale a partire dalla base dati remota che offre la cooperazione.
In tutte le precedenti forme di cooperazione, questa viene instaurata operando sulle basi esistenti con nuovi componenti architetturali. Nei data warehouse (magazzini o depositi di dati) viene creata (periodicamente) una nuova base dati, che nasce dall'integrazione stretta delle basi di dati esistenti, e tale nuova base dati viene resa accessibile con potenti linguaggi per l'analisi e l'estrazione di informazioni rilevanti a fini decisionali. Il vantaggio di questa soluzione è nel tenere separati i dati operativi da quelli su cui vengono fatte interrogazioni e analisi, senza perdere i benefici dell'integrazione; lo svantaggio è nell'aggravio gestionale derivante dalla necessità di creare una nuova base dati.
Una prima tipologia di tecnologie per la cooperazione tra applicazioni è rappresentata dalle architetture cliente servente (client server), in cui differenti risorse di elaborazione (elaboratori, periferiche ecc.) connesse in una rete possono chiedere e ottenere, cioè scambiarsi, servizi; da qui il nome cliente (che chiede un servizio, per es. una stampa o l'accesso a una base di dati), e servente (che lo fornisce). Un'architettura cliente servente può vedersi come una tipica architettura di cooperazione, perché permette di mettere in comune, scambiare servizi tra poli elaborativi altrimenti isolati. I sistemi cooperativi basati su broker (intermediatori) o agenti sono un'evoluzione dei sistemi cliente servente, nel senso che prevedono la presenza di terze parti, i broker, che facilitano la cooperazione tra gli utenti del sistema. L'intermediazione può avvenire utilizzando come strumento di descrizione dei servizi di cooperazione un modello orientato a oggetti. Un modello, nelle tecnologie dell'informazione, è un insieme di strutture di rappresentazione che permette di descrivere un aspetto della realtà osservata in modo da renderlo elaborabile in un sistema di calcolo.
I modelli orientati a oggetti cercano di superare il dualismo presente nei precedenti modelli informatici, prevalentemente orientati alla descrizione o dei dati o delle applicazioni, proponendo un modello descrittivo unificato per i due aspetti, che ha come concetto primario quello di oggetto. Un oggetto è un'entità univocamente identificabile nel sistema (per es., una persona, una fattura o un ordine, un quadro), dotato di caratteristiche strutturali e di caratteristiche comportamentali.
Le caratteristiche strutturali descrivono le proprietà statiche dell'oggetto, e possono essere attributi (per una persona: il nome, il codice fiscale, la data di nascita), o riferimenti ad altri oggetti (per una persona: la relazione 'nato a', che la collega con un oggetto 'città'; per una fattura, la relazione 'fa riferimento a', che la collega a un ordine).
Le caratteristiche comportamentali sono le operazioni o funzioni che determinano il comportamento dell'oggetto, cioè le sue trasformazioni, e sono espresse da metodi (per una persona, un metodo è 'modifica la residenza'; per una fattura, un metodo è 'verifica importo'). Gli oggetti si raggruppano in classi omogenee (le persone, le fatture, gli ordini). Gli oggetti e le classi di oggetti interagiscono tra loro per mezzo di messaggi, che invocano l'attivazione di metodi (un esempio di messaggio è 'modifica la residenza di Rossi da Roma a Milano'). Gli oggetti e le classi possono essere organizzati in termini di gerarchia di ereditarietà: per es., la classe 'impiegato' può esser vista come una sottoclasse della classe 'persona'. Come tale, eredita tutte le proprietà della classe 'persona', e può averne associate altre (per es., tra gli attributi, lo stipendio e il tipo di lavoro, tra i metodi, 'aggiorna stipendio').
Accanto ai modelli, si sono sviluppati sistemi di gestione orientati a oggetti, che possono vedersi come un'estensione dei sistemi di gestione di basi di dati, nei quali la grande novità è data dal fatto che negli oggetti aspetti strutturali e comportamentali sono integrati.
Un'altra importante caratteristica dei sistemi orientati a oggetti consiste nel permettere in modo naturale una separazione della specifica dell'oggetto (cioè le sue caratteristiche) dall'implementazione, cioè dal modo in cui la sua struttura e i metodi e messaggi sono espressi per mezzo del software operante nel sistema di calcolo.
L'insieme di caratteristiche descritto rende i sistemi a oggetti naturali candidati per realizzare architetture di cooperazione. Queste, chiamate anche broker, prevedono che ogni sistema in rete che intenda mettere a disposizione i propri servizi (informazioni e funzioni elaborative), avendo come contropartita la possibilità di accedere a quelli degli altri sistemi, debba rappresentarli per mezzo di oggetti, secondo il modello adottato. Il broker, che può essere a sua volta centralizzato presso un sistema ovvero distribuito su più sistemi, ha il compito di permettere la soddisfazione della richiesta, stabilendo la relazione logica tra richiedente e offerente.
Modalità di distribuzione cooperativa dei servizi sono possibili anche con altre soluzioni tecnologiche, tutte basate sullo sviluppo di componenti architetturali di middleware (o strato intermedio di software). Il middleware, indipendentemente dalle specifiche soluzioni tecnologiche, è uno strato di software che si interpone tra funzionalità inizialmente non interoperabili per fare in modo che possano ciascuna usufruire dei servizi messi a disposizione dall'altra. In questa accezione, i sistemi orientati a oggetti e le altre soluzioni basate su middleware adottano un paradigma di interazione superiore e più evoluto e generale di quello tipico delle prime architetture cliente servente, spesso definito come pari a pari o paritario. Una conseguenza importante delle soluzioni esposte è quella di risolvere il problema dei sistemi ereditati dal passato: è infatti in linea di principio possibile procedere a una migrazione dalle soluzioni proprietarie, e in diversi casi tecnologicamente obsolete, realizzando inizialmente lo strato di intermediazione senza modificare il sistema esistente, e procedendo successivamente a una modifica del sistema legacy senza che gli utenti (e diversi strati software) percepiscano mutamenti nell'interazione e nell'operatività.
I sistemi e le architetture moderni possono essere visti come un'evoluzione dei sistemi transazionali classici, in cui un'interazione con il sistema da parte di un utente o di una funzione elaborativa è soggetta a totale o estesa automazione, frammentandola eventualmente in accessi ed elaborazioni distribuite, che però fanno parte di un unico processo elaborativo. Molte attività che prevedono l'elaborazione di informazioni richiedono in realtà la cooperazione tra utenti o processi che in diversi periodi temporali compiono sequenze di attività manuali e automatiche. I sistemi di gestione del flusso di lavoro (workflow management system) hanno lo scopo di fornire tali ausili. Essi hanno anzitutto la capacità di modellare il flusso delle attività, descrivendo per ogni fase gli agenti (utenti e funzioni applicative) coinvolti nella fase, i documenti di input, i documenti di output, gli eventi attivatori della fase, le proprietà del sistema che devono essere valide all'inizio e alla fine della fase (chiamate anche precondizione e postcondizione), le situazioni di eccezione che devono essere attivate quando qualche pre- o postcondizione non è verificata, i legami causali tra fasi. Avendo la possibilità di descrivere tutti gli aspetti messi in evidenza, il sistema di gestione del flusso di lavoro può aiutare gli agenti coinvolti nel processo a cooperare nella sua esecuzione, sostituendoli o svolgendo un ruolo attivo sia in alcune fasi della propria attività, sia nelle interazioni che sono necessarie tra gli agenti per condurre in modo efficiente (cioè con ragionevole uso di risorse) ed efficace (cioè ottenendo i risultati previsti) il processo.
Nel precedente scenario, entra prepotentemente Internet (v. spazio informatico, App. V, e rete, in questa Appendice). Il presupposto tecnologico che ha permesso la travolgente crescita di Internet è stato (fig. 6) l'iniziale adozione di un protocollo di connessione semplice ed efficiente al tempo stesso, il protocollo TCP/IP (Transmission Control Protocol/Internet Protocol, protocollo di controllo trasmissione/protocollo Internet). La sua caratteristica fondamentale è quella di permettere in forma affidabile la connessione di reti eterogenee, cioè inizialmente sviluppate mediante protocolli di comunicazione proprietari, realizzati da specifiche ditte. E in effetti 'essere su lnternet' corrisponde spesso ad adottare il protocollo TCP/IP, e a disporre di un indirizzo IP, cioè a essere identificabile con un indirizzo, così come il nostro recapito è identificato da una via, un numero civico ecc.
I servizi resi disponibili tramite Internet sono ormai molti, ma tra essi vengono distinti i seguenti principali: posta elettronica (sviluppata anche nell'ambito di altre tecnologie, ma che ha avuto in Internet uno sviluppo vorticoso), cioè la capacità di comporre, inviare e ricevere messaggi di posta a uno o più indirizzi di utenti sulla rete, scambiati e ricevuti in tempi e costi straordinariamente inferiori (pochi secondi, poche lire) rispetto alla posta tradizionale; collegamento remoto, la possibilità di collegarsi a uno qualunque degli elaboratori connessi in rete per usufruire dei servizi resi disponibili; trasferimento di archivi, la possibilità di copiare archivi (articoli, libri, pubblicazioni, basi di dati, immagini) da un qualunque elaboratore sul proprio elaboratore personale; la world wide web (letteralmente, ragnatela mondiale), applicazione che sta uguagliando e superando per numero di accessi la posta elettronica, e che sta avvicinando alla rete nuove tipologie di utenti. La web è una rete mondiale di informazioni, accessibili mediante due meccanismi di accesso principali e omogeneamente diffusi in tutta la rete, l'indirizzo della pagina di ingresso (o home page), e un insieme vastissimo di puntatori associati a parole o a icone, che rimandano ad altri indirizzi o pagine a essi concettualmente collegati (da cui la dizione 'ragnatela', intesa come una continua rete di collegamenti logici su cui è possibile navigare), adottando in questo modo il paradigma degli ipertesti (cioè testi che descrivono al loro interno relazioni concettuali con altri testi), che a sua volta è ispirato alle modalità conoscitive del pensiero associativo.
La tecnologia che permette di garantire un'elevata interoperabilità, cioè la possibilità di interazione tra piattaforme tecnologiche diverse sulla rete, è quella dei browser (navigatori), programmi di elaborazione, ricerca e visualizzazione residenti sia sugli elaboratori clienti sia sui serventi, che interpretano le richieste dei clienti, acquisiscono le risposte dei serventi in un linguaggio da interpretare e traducono la risposta in termini della piattaforma tecnologica disponibile presso il cliente.
La rete Internet sta assumendo un ruolo di 'attrattore tecnologico' di altre tecnologie. Nell'ambito di queste, hanno avuto particolare diffusione i linguaggi programmativi e gli ambienti di sviluppo (per es., Java), che garantiscono una totale compatibilità con tutte le piattaforme tecnologiche esistenti per sistemi operativi e software di ambiente. A titolo esemplificativo, una tipica soluzione è quella di linguaggi a oggetti (che garantiscono dunque il riuso delle applicazioni e le modalità di cooperazione trattate in precedenza) di tipo interpretato, cioè le cui istruzioni siano tradotte in linguaggio eseguibile dall'elaboratore al momento di esecuzione. La portabilità (come nel caso dei browser) è garantita dal fatto che l'interpretazione è fatta dall'ambiente di esecuzione. Con quest'approccio è possibile far navigare sulla rete, a richiesta dell'utente ovvero per esigenze elaborative connesse all'interazione con la pagina web, programmi eseguibili, rivoluzionando completamente l'approccio tipico in cui il software applicativo richiesto dall'utente o da un'organizzazione si sviluppa in anni di lavoro ovvero si compra e si personalizza, e passando a un paradigma orientato all'utilizzo cooperativo di programmi (il cosiddetto freeware, software gratuito), ovvero al loro affitto, tutte e sole le volte in cui servirà. Le soluzioni del 'paradigma tecnologico' Internet sono spesso adottate da singole organizzazioni per il proprio sistema informativo. Si parla allora di intranet (internet interna), quando si fa riferimento alla rete utilizzata per i processi interni all'organizzazione, e di extranet (rete esterna) quando si fa riferimento alla rete utilizzata per la comunicazione con i clienti e utenti esterni.
Il problema della sicurezza. - Un'importante tematica che le tecnologie dell'informazione hanno affrontato riguarda la sicurezza dei sistemi, particolarmente critica per i sistemi distribuiti. Per sicurezza si intende l'insieme di caratteristiche (di tipo organizzativo e tecnologico) tese ad assicurare a ciascun utente autorizzato (e a nessun altro) tutti e soltanto i servizi destinati a quell'utente, nei tempi e nelle modalità previsti. Le tre proprietà o qualità in cui s'incardina la sicurezza sono la disponibilità (il sistema deve rendere disponibili a ciascun utente abilitato le informazioni alle quali ha diritto di accedere, nei tempi e nei modi previsti), l'integrità (il sistema deve impedire l'alterazione diretta o indiretta delle informazioni, sia da parte di utenti e processi non autorizzati, sia a seguito di eventi accidentali), e la riservatezza (nessun utente deve ottenere o dedurre dal sistema informazioni che non è autorizzato a conoscere).
Gli attacchi che possono minare la sicurezza del sistema possono essere effettuati sui diversi strati architetturali del sistema informatico, e cioè rete di comunicazione, sistema operativo, software di sistema, software applicativo, basi di dati, e possono, a seconda della tecnica adottata, essere classificati in intercettazioni e deduzioni (attacchi alla riservatezza), intrusioni (attacchi all'integrità e riservatezza), disturbi (attacchi alla disponibilità).
Poiché nella malizia e nei reati non vi è limite all'inventiva, possiamo solo procedere per esempi. Le tecniche di intercettazione possono basarsi su analizzatori di traffico, server pirata che si spacciano per gestori della trasmissione, programmi che emulano diversi servizi del sistema. Le tecniche di deduzione si basano sulla possibilità di correlare logicamente informazioni poco riservate acquisite da diverse fonti, per dedurre informazioni riservate. Le tecniche di intrusione possono basarsi su accesso con una parola chiave di altro utente, ovvero con l'installazione nel sistema di un demone, cioè un programma software che garantisce, finché non viene individuato, la possibilità di accessi illegali anche se in precedenza il primo attacco è stato scoperto e, apparentemente, risolto. Le tecniche di disturbo possono procedere con lo scopo di degradare l'operatività del sistema: le più note sono i cosiddetti virus.
Nelle reti, e in particolare nella rete Internet, le proprietà specifiche che si devono rispettare per la sicurezza nella fruizione dei servizi disponibili (e che possono essere viste come sottospecificazioni delle precedenti) sono l'autenticità (chi accede a determinate risorse messe a disposizione sulla rete è veramente chi afferma di essere), il controllo dell'accesso (verifica dei privilegi di accesso alle diverse risorse), la confidenzialità dei messaggi (impossibilità di effettuare intrusioni), l'integrità dei messaggi (impossibilità di modifica), il non ripudio dei messaggi (chi firma il messaggio non può svincolarsi dall'obbligo instaurato con il suo invio).
La multimedialità
Le tecnologie per la multimedialità riguardano i sistemi che creano, elaborano, memorizzano, presentano e trasferiscono le informazioni in molteplici rappresentazioni, o media. Tali media sono classificabili, a seconda del senso umano attraverso cui avviene l'interazione, in media ottici e acustici. I media ottici sono classificabili in testi (composizioni di simboli alfabetici) e immagini, che possiamo distinguere in grafici (rappresentazioni simboliche di modelli descrittivi di figure geometriche e iconiche a diverso livello di sofisticazione), animazioni (immagini grafiche in movimento), immagini realistiche (rappresentazioni di scene o aspetti del mondo sensibile). Le immagini possono esse fisse o in movimento. I media acustici sono classificabili in parlato (che corrisponde a una codifica uditiva di linguaggi di comunicazione verbale), musica (codifica uditiva di un sistema a note strutturato), suoni (codifiche uditive di tipo generale, non vincolate a linguaggi o modelli sottostanti), e infine quella che sempre più spesso è chiamata la realtà virtuale (v. App. V), in cui è rappresentato un mondo complesso e articolato spazialmente e strutturalmente, insieme alla sua evoluzione temporale. Più propriamente, per realtà virtuale s'intende l'insieme di tecnologie che permettono all'utente, o a un gruppo di utenti, di immergersi in un ambiente tridimensionale che si evolve dinamicamente, interagire con esso ed esplorarlo.
Si sta poi diffondendo nelle tecnologie multimediali (soprattutto per la realtà virtuale) la possibilità di cogliere altri aspetti via via più sofisticati della comunicazione e interazione umana, quali la forza fisica, i movimenti delle mani e della testa, l'olfatto, alcuni aspetti del pensiero e della mente. Per questo tipo di interazione si stanno sviluppando strumenti quali mouse tridimensionali, tracciatori tridimensionali, occhiali stereoscopici, caschi, guanti, strumenti basati sui gesti, sul tatto e sulla forza, interfacce basate sul tono della voce.
Nelle tecnologie per la rappresentazione ed elaborazione di immagini, queste possono essere rappresentate come matrici bidimensionali di punti (rappresentazione a bitmap), di diverso colore e intensità luminosa (in questo caso il modello descrittivo è molto elementare, un insieme di punti), ovvero mediante oggetti matematici come linee, curve, superfici ecc. (rappresentazione vettoriale). La rappresentazione a bitmap è meno compatta della rappresentazione vettoriale, ma è anche la più semplice da acquisire e memorizzare partendo da strumenti di scansione di immagini analogiche o a fotorilevazione. La rappresentazione vettoriale permette di associare un significato alle immagini (per es., una spezzata è un'autostrada, una superficie è un lago ecc.), e dà la possibilità di utilizzare linguaggi di ricerca più potenti. Le tecniche di rilevazione rendono progressivamente più semplice la trasferibilità delle immagini tra le due rappresentazioni. I colori delle immagini vengono solitamente rappresentati utilizzando o la teoria del tristimulus, specificando la tonalità tramite tre componenti, per es. giallo, rosso e blu, ovvero specificando la luminanza e la crominanza. La profondità di colore corrisponde all'insieme dei colori rappresentabili, che è ormai spesso equivalente all'insieme dei colori percepibili dall'occhio umano (oltre 16 milioni).
Le funzionalità più diffuse per le immagini grafiche sono tutte le tradizionali funzioni geometriche quali la traslazione, la rotazione, la trasformazione isomorfa e non isomorfa, la deformazione, il ritaglio, l'intersezione di superfici, la definizione delle superfici nascoste, il raggruppamento di oggetti, la produzione automatica del grafo (rispettando regole estetiche, metriche e topologiche), l'elaborazione di sequenze di forme e di gruppi di forme secondo regole e vincoli spaziali e temporali.
Nella realtà virtuale vengono distinti due tipi di sistemi, rispettivamente immersivi, in cui la persona è completamente inserita nella realtà virtuale con cui vuole interagire, e non immersivi, in cui l'interfaccia offre comandi meno 'naturali', ma permette di operare anche su oggetti lontani. Il vantaggio dell'approccio immersivo sta nella naturalezza con cui simula la situazione reale, il suo limite nel fatto che per operare su oggetti distanti è necessario navigare nella realtà virtuale fin quando l'oggetto viene raggiunto.
Le funzionalità più diffuse per le immagini realistiche e per la realtà virtuale sono la coloritura, la rappresentazione della voluminosità, l'illuminazione o l'ombreggiatura di oggetti e scene, l'estrazione di regioni od oggetti, la tracciatura di regioni in sequenze di immagini, il calcolo di trasformazioni od omotopie di oggetti, l'elaborazione di sezioni di oggetti, o di insiemi di punti caratterizzati da proprietà comuni, l'elaborazione del movimento di oggetti, la composizione di scene, la realizzazione di collegamenti tra differenti media (ipermedialità). Per le due rappresentazioni sono particolarmente importanti le tecniche di compressione che permettono di ridurre di diversi ordini di grandezza la memoria necessaria a immagazzinare i dati. I metodi di compressione possono essere classificati in metodi senza perdita e con perdita. I primi sono utilizzabili con entrambi i tipi di rappresentazioni, si basano sulle similitudini presenti nell'immagine (per es. una linea o superficie regolare con tutti bit dello stesso colore può essere rappresentata con le coordinate di riferimento della linea o superficie, più il colore), permettono di ricostruire completamente l'immagine, ma forniscono ridotti rapporti di compressione. I secondi raggiungono anche rapporti 1 a 1000, e utilizzano varie tecniche ed enti matematici, tra cui i frattali (v. App. V).
Le problematiche multimediali riguardano ormai ogni aspetto delle tecnologie hardware e software. Le architetture hardware devono fornire livelli di parallelismo in grado di garantire efficienza di esecuzione su grandi quantità di dati, i sistemi operativi devono adottare più efficienti modalità di scelta dei processi elaborativi per garantire i tempi di esecuzione necessari, i sistemi di gestione di basi di dati devono trasformarsi in sistemi di gestione di oggetti complessi, con modalità di memorizzazione e di indirizzamento di tali oggetti più potenti di quelle tradizionali, le reti di trasmissione devono garantire una banda di comunicazione e protocolli di instradamento più efficienti.
Le applicazioni più tipiche delle tecnologie multimediali riguardano la telemedicina, le scienze ingegneristiche, fisiche e geologiche, le arti, la teleconferenza, il telelavoro, la formazione assistita da calcolatore, le biblioteche digitali, il commercio elettronico, l'intrattenimento, i giochi elettronici. In tutte queste applicazioni, il requisito dell'interattività, cioè della possibilità per l'utente di interagire con l'applicazione esprimendo richieste, esige tecnologie e canali di comunicazione simmetrici tra sorgente e destinazione. La stessa rete Internet, con la sua capacità di attrarre tecnologie innovative, è ormai un'immensa realtà virtuale, dove sono disponibili pagine che rappresentano (ovvero navigano programmi che elaborano) immagini, suoni, video.
Le tendenze future
Stabilire le tendenze a medio e lungo termine delle tecnologie dell'informazione è ancor più rischioso che descriverne l'attuale evoluzione, e richiede una sia pur sommaria analisi del mercato produttivo. Circa le tecnologie per l'i. personale, le più promettenti riguardano il mobile computing e il wearable computing. Per mobile computing (elaborazione mobile) s'intende la possibilità di disporre di un elaboratore avente la stessa potenza e funzionalità del personal, ma collegabile con una rete. Per wearable computing (elaborazione vestibile) s'intendono tutte le tecnologie realizzate per essere vestite o incorporate dalla persona, e che quindi costituiscono 'protesi tecnologiche' del corpo e della mente.
Le tecnologie per i sistemi distribuiti saranno sempre più interoperabili, cioè realizzate in modo tale da essere utilizzabili congiuntamente, indipendentemente dal produttore originario. A livello mondiale, è visibile la progressiva integrazione delle piattaforme di produttori di hardware, sistemi operativi, basi di dati, soluzioni Internet, linguaggi. Questo fenomeno, la cui proiezione futura è intuibile negli sviluppi attuali, è forzato anche dagli acquirenti importanti (gli Stati, le grandi organizzazioni del credito diffuse a livello mondiale, le pubbliche amministrazioni) che intendono conservare gli investimenti per un periodo ragionevolmente più lungo dell'attuale. Non è chiaro se uno degli approcci descritti risulterà vincitore (e quale, nel caso), ed è piuttosto prevedibile un insieme di cicli in cui nuovi 'paradigmi tecnologici' si aggiungeranno ai precedenti, con la spinta a raggiungere nuovi livelli di interoperabilità. Ciò forzerà nuove alleanze tra produttori, con sviluppi imprevedibili, ma che dovrebbero portare alla sopravvivenza di pochi cartelli e molti produttori di nicchia. Un arricchimento prevedibile delle tecnologie cooperative sarà nella direzione dello sviluppo di agenti attivi, che sulla base della conoscenza delle esigenze di un dato campione di utenti o della specifica di un'applicazione informatica, interverranno nell'individuazione all'interno della rete delle informazioni necessarie, ovvero sostituiranno utenti e applicazioni nell'effettuazione di specifiche operazioni.
I sistemi di gestione dei dati si evolveranno in diverse direzioni che colmeranno gli attuali limiti: la possibilità di esprimere il tempo come caratteristica primaria del sistema, e di effettuare interrogazioni ed elaborazioni su di esso, la possibilità di far evolvere la stessa struttura (o schema) dei dati oggetto di gestione (per es., l'estensione dinamica di un oggetto con nuovi metodi e nuove proprietà), l'estensione delle caratteristiche rappresentabili verso la descrizione di regole, la possibilità di riconciliare le inconsistenze di rappresentazione e, nella semantica dei dati, l'introduzione di ipotesi di mondo aperto (in contrasto con l'attuale tipica ipotesi di mondo chiuso, per cui se un'informazione non è rappresentata nella base di dati, essa è assunta non valida o non esistente nella realtà rappresentata), la capacità di trovare regolarità o leggi in insiemi di dati (data mining, cioè estrazione di materiale prezioso dai dati).
Malgrado i notevoli progressi introdotti nel dialogo uomo macchina dall'utilizzo delle interfacce utente, rimangono nelle soluzioni attuali molte limitazioni. Per quanto amichevole verso l'utente (user friendly), un'interfaccia resta pur sempre un intermediario tra l'intenzione dell'utente e l'esecuzione di tale intenzione. In questo senso, la più efficace interfaccia è l'assenza stessa di interfaccia. Le tecnologie si stanno pertanto orientando verso interfacce adattive in grado di costruire, attraverso l'interazione, un profilo dell'utente e verso modalità di interazione che operino un radicale mutamento rispetto al paradigma WIMP. Le cosiddette interfacce post-WIMP si basano sull'uso della gestualità e sul riconoscimento del parlato per la comprensione dei comandi e delle interazioni. Ma per raggiungere l'ideale situazione in cui l'interfaccia è abolita perché i due soggetti (utente ed elaboratore) si intendono anche senza scambiarsi messaggi o comandi, è necessario studiare nuovi paradigmi, come per es. quello 'del maggiordomo', in cui l'elaboratore conosce discretamente la personalità dell'utente, le sue esigenze, le sue idiosincrasie, al punto di anticiparne silenziosamente le intenzioni.
Per le applicazioni multimediali e di realtà virtuale, i problemi più critici riguardano lo sviluppo di architetture, strumenti di ingresso e di uscita, reti, algoritmi, euristiche (cioè strategie approssimate) che permettano di stabilire un'interattività realistica tra la persona e la tecnologia, garantendo errori accettabili nella rilevazione dell'input e nella produzione dell'output, e tempi di latenza e di reazione dell'ambiente virtuale paragonabili a quelli dell'essere umano (da 0,01 a 0,2 secondi).
Affinché le reti possano diventare fruibili per ogni individuo, e non soltanto per quelli culturalmente evoluti e quelli appartenenti a nazioni industrialmente avanzate, sarà necessario sviluppare strategie più sofisticate per la ricerca dell'informazione, interfacce che trasformino automaticamente le informazioni nel linguaggio nativo dell'utente, meccanismi di puntamento ipertestuale dotati di una semantica più potente di quella attuale e che permettano, per es., di collegare per tematiche e non solo in modo esatto, ma anche con una certa approssimazione.
bibliografia
A.S. Tanembaum, Computer networks, Englewood Cliffs 1981, Upper Saddle River (N.J.) 1996³ (trad. it. Milano 1981; Torino 1997).
C. Ghezzi et al., Ingegneria del software: progettazione, sviluppo e verifica, Milano 1991.
J.L. Encarnacao, J.D. Foley, Multimedia: system architectures and applications, Berlin-New York 1994.
J.A. Larson, Database directions: from relational to distributed, multimedia, and object oriented database systems, Upper Saddle River (N.J.) 1995.
ACM 50th anniversary symposium: perspectives in computer science, in ACM computing surveys, 1996, 1, nr. monografico.
P. Atzeni, S. Ceri, S. Paraboschi et al., Basi di dati: concetti, linguaggi e architetture, Milano 1996.
R. Orfali, D. Harkey, J. Edwards, The essential distributed objects survival guide, New York 1996.
50 years of computing, in Computer, 1996, 10, nr. monografico.
The next 50 years: our hopes, our visions, our plans, in Communications of the ACM, 1997, 2, nr. monografico.
Informatica e diritto
di Vittorio Frosini
Nel vasto campo di applicazioni che l'i. - come tecnica di memorizzazione, aggregazione e comunicazione di informazioni automatizzate con sistema elettronico - ha avuto nella seconda metà del 20° secolo, figura anche il contributo recato al progresso degli studi e della pratica del diritto.
Al nuovo termine informatica, coniato nel 1962 dal francese Ph. Dreyfus, venne associato l'aggettivo giuridica nella cultura dei paesi dell'Europa continentale, mentre nei paesi di lingua anglosassone venne usato agli inizi il termine jurimetrics, proposto dallo statunitense L. Loevinger nel 1949 per indicare l'utilizzazione dei metodi della tecnologia elettronica nel campo della giurisprudenza. Lo stesso Loevinger fu il primo anche a dare un'applicazione pratica della dottrina da lui formulata, installando (1962) nel Department of Justice del governo federale statunitense un calcolatore programmato per una ricerca a fini fiscali, che venne denominato LEX.
Negli anni Sessanta la metodologia di raccolta e di ricerca automatizzata dei dati venne estesa all'informazione e classificazione dei precedenti giudiziari, così importanti nel sistema giuridico anglosassone di case law. Questo indirizzo di applicazione dell'i. al diritto esercitò la sua influenza sulle successive esperienze europee, caratterizzando l'informatica giuridica come i. documentaria, che venne rivolta alla ricerca del 'dato giuridico globale', ossia di un'informazione comprensiva degli elementi legislativi, giudiziari e dottrinali (in forma bibliografica) riferiti a una figura giuridica o a un caso pratico. In Italia, il 21 marzo 1969 fu presentato un modello di ricerca elettronica dei precedenti giurisprudenziali, elaborato dai magistrati dell'Ufficio massimario della Corte di cassazione.
Venivano intanto pubblicati i primi studi sull'argomento, avviati sin dal 1959 negli Stati Uniti e ai quali offriva subito il proprio contributo anche la dottrina italiana.
Il diritto alla riservatezza
Con la diffusione degli elaboratori elettronici, nei quali con i caratteri alfanumerici fu possibile inserire, oltre alle cifre numeriche, anche le parole, e con la creazione di raccolte di dati informativi sulle persone, si configurò una nuova forma di potere sociale, il potere informatico, consistente nel possesso di informazioni sulla vita privata anche di chi non sia a conoscenza delle violazioni della sua riservatezza; un possesso che, per quantità, varietà, possibilità di aggregazione e confronto dei dati, ha oltrepassato di gran lunga tutti i precedenti metodi di indagine. Fu perciò invocato il right to privacy, o diritto alla riservatezza della propria vita privata, che era stato formulato nel 1891 da L. Brandeis e S. Warren per difendersi dall'invadenza della cronaca sulla stampa quotidiana; esso fu considerato come un nuovo diritto di libertà personale, e riferito ai sistemi di informazione automatizzata. Il primo riconoscimento giuridico del right to privacy in questa forma comparve nel Fair Reporting Act 1970 emanato negli Stati Uniti e riguardava i rapporti fra privati; nello stesso anno fu pubblicata nel Land dell'Assia (Repubblica federale tedesca) la prima legge sulla protezione dei dati del cittadino nei confronti della pubblica amministrazione, e venne anche istituito un apposito organo di sorveglianza.
Nel corso degli anni Settanta e Ottanta si susseguirono in Europa gli interventi legislativi rivolti a tutelare il nuovo diritto della persona; essi trovarono la loro composizione e, in certo modo, la loro celebrazione nella Convenzione europea sulla protezione dei dati personali, aperta alla firma degli Stati membri il 18 gennaio 1981. Nello stesso anno, a opera della dottrina italiana, veniva formulato il 'diritto di libertà informatica' come nuovo diritto di libertà personale apparso nell'età tecnologica: nell'ambito del diritto di informazione, inteso come diritto di informare e di essere informati, la libertà informatica configurava il diritto specificato del singolo.
La tutela dei dati personali
L'Italia, pur avendo aderito alla Convenzione europea sopra ricordata, tardò a ratificarla, ossia ad accoglierla nel proprio ordinamento giuridico come legge propria; finché, sollecitato dall'emanazione di una Direttiva europea sulla stessa materia del 24 ottobre 1995, che sarebbe divenuta legge in vigore anche per l'Italia entro il 23 ottobre 1998, il Parlamento italiano provvide a sua volta a emanare una legge sulla tutela dei dati personali (estesi però fino a comprendere quelli delle persone giuridiche e persino delle associazioni non riconosciute), l. 31 dic. 1996 nr. 675, accompagnata dalla l. nr. 676, in pari data, di delega al governo in materia.
In conformità alle disposizioni contenute nella Direttiva europea, anche nella legge italiana vengono identificati, come meritevoli di speciali forme di garanzia giuridica, i cosiddetti 'casi sensibili': quelli idonei a rivelare l'origine razziale o etnica, le convinzioni religiose, filosofiche o di altro genere, le opinioni politiche, l'adesione a partiti, o sindacati, o associazioni od organizzazioni a carattere religioso, filosofico, politico o sindacale; nonché i dati personali idonei a rivelare lo stato di salute o la vita sessuale. Per evitare l'indebita raccolta, aggregazione, utilizzazione e diffusione di tali dati, la legge ha predisposto particolari forme di tutela, la cui osservanza (con eventuali deroghe) è sottoposta al controllo di un'apposita autorità indipendente, l'Ufficio del Garante per la protezione dei dati, composto da quattro membri, fra i quali viene eletto un presidente (v. riservatezza, in questa Appendice).
Con la legge citata, la nozione del diritto di libertà informatica ha trovato il suo riconoscimento nel diritto positivo; essa ha però subito una trasformazione, giacché il diritto di tutelare i propri dati si attua nei confronti di qualunque trattamento di essi, anche non elettronico, e muta il suo carattere, prima ispirato al principio della difesa dinanzi agli abusi del potere informatico, ora considerato come un diritto attivo di partecipazione del cittadino al circuito delle informazioni.
L'informatica nella pubblica amministrazione
Con l'avvento dei sistemi elettronici di assemblaggio e trasmissione dei dati, si è configurata una nuova forma di burocrazia, ignota alle età precedenti, che pure avevano raggiunto livelli di grande complessità: con l'integrazione uomo-macchina si realizza l'automazione amministrativa, denominata burotica. Il suo annuncio venne dato in Italia dalla circolare del 6 marzo 1968, nr. 456.1.12, della Presidenza del Consiglio dei ministri "per il coordinamento delle attività dei Centri meccanografici ed elettronici presso le amministrazioni statali". Trascorsero tuttavia diversi anni prima che il processo di informatizzazione degli uffici pubblici si sviluppasse con una certa regolarità (mentre procedeva rapidamente quello degli uffici privati); la messa in funzione del nuovo apparato burocratico è stata segnata dal d. legisl. del 12 febbr. 1993 nr. 39, contenente le norme in materia di sistemi informativi automatizzati delle amministrazioni pubbliche.
L'i. giuridica, intesa sia in senso tecnico-strumentale sia in senso normativo-regolamentare, si è dunque estesa a coprire il campo dei rapporti fra il cittadino e gli organi amministrativi. Il decreto del 1993 ha istituito perciò un'Autorità per l'Informatica nella Pubblica Amministrazione (AIPA), che opera presso la Presidenza del Consiglio dei ministri con autonomia tecnica e funzionale e con indipendenza di giudizio, ed è costituita da un presidente e quattro membri. Essa provvede a organizzare i sistemi informativi automatizzati delle amministrazioni pubbliche, a fare opera di vigilanza, di attuazione e di verifica dei risultati, a esercitare ogni funzione utile a ottenere un più razionale impiego dei sistemi informativi. Il collegamento telematico fra i diversi uffici ha dato forma alla 'teleamministrazione'.
Fra le novità rilevanti del decreto, vi è la disposizione che "gli atti amministrativi adottati da tutte le pubbliche amministrazioni sono di norma predisposti tramite i sistemi informativi automatizzati", e che la firma autografa del funzionario è sostituita dall'indicazione a stampa del nominativo.
La tutela dei programmi
Accanto alle nuove prospettive e ai nuovi problemi relativi alla tutela dei dati personali e ai rapporti fra il cittadino e gli uffici pubblici, l'impiego della metodologia informatica ha imposto alla società tecnologica il riconoscimento di un nuovo bene giuridico, consistente nel trattamento di dati e nella loro trasmissione telematica, con cui si realizza un nuovo valore aggiunto all'informazione: ossia della produzione, circolazione e consumo del bene informatico. Il dibattito in sede giurisprudenziale e in sede dottrinaria, che ha avuto i suoi effetti sulla legislazione e sugli accordi internazionali, riguardava soprattutto la protezione da accordare ai programmi, cioè alla macchina logica (software) che incorporata nella macchina materiale (hardware) la mette in funzione, e, in particolare, la miglior tutela del programma, con il ricorso alle norme che proteggono il brevetto industriale (patent), ovvero a quelle relative al diritto d'autore (copyright).
Tuttavia, il 5 ottobre 1973 venne firmata a Monaco la European Patent Convention, che escludeva dalla brevettabilità i programmi per computer; nel giugno 1988 venne pubblicato il Libro verde sul diritto d'autore e le sfide tecnologiche della Commissione della Comunità Europea, che esaminava dettagliatamente il problema, e che indirizzò verso la soluzione dell'adozione del copyright la successiva Direttiva 91/250 CEE; essa trovò attuazione nel sistema giuridico italiano con il d. legisl. 29 dic. 1992 nr. 518, che emanò una serie di modifiche e aggiunte alla legge sul diritto d'autore del 22 aprile 1941 nr. 633. Con tale decreto venne istituito un registro pubblico speciale per i programmi per elaboratore tenuto presso la Società italiana autori ed editori (SIAE), con facoltà (non obbligo) di registrazione di un programma; fu inoltre prevista come reato, punito con le pene della reclusione e della multa, la riproduzione abusiva di un programma a fini di lucro.
La criminalità informatica
Con l'avvenuta irruzione dei computer nel mondo dei rapporti economici e sociali si sono verificati profondi mutamenti nella società umana, con i connessi vantaggi e inconvenienti: fra questi ultimi, vi è stata l'apparizione di un nuovo tipo di criminalità, definito nella dottrina italiana reato informatico. È sorta perciò una legislazione penale sugli usi illeciti dell'i., emanata in diverse nazioni europee, alla quale si è aggiunta quella italiana con l. 23 dic. 1993 nr. 547.
Tale legge non ha costituito un intervento radicalmente innovativo, ma ha comunque introdotto significative modifiche e integrazioni al codice penale per contrastare i fenomeni sempre più diffusi di criminalità informatica. È stato in primo luogo precisato, ai fini dell'applicazione delle disposizioni sulla falsità in atti (artt. 476-491 c. p.) e della norma sulla rivelazione del contenuto di documenti segreti (art. 621), il concetto di documento informatico, inteso come qualsiasi supporto informatico contenente dati, informazioni o programmi. Per quanto riguarda la falsità in atti, le relative disposizioni si applicano ai documenti informatici pubblici o privati, qualora gli stessi contengano dati o informazioni aventi efficacia probatoria o programmi specificamente destinati a elaborarli (art. 491 bis). La violenza sulle cose, rilevante ai fini dell'ipotesi di esercizio arbitrario delle proprie ragioni (art. 392), sussiste anche quando un programma informatico venga alterato, modificato, cancellato in tutto o in parte, ovvero venga impedito o turbato il funzionamento di un sistema informatico o telematico. La violazione, sottrazione o soppressione di corrispondenza è punibile anche quando sia effettuata per via informatica o telematica, ovvero con ogni altra forma di comunicazione a distanza (art. 616, 4° comma). Il delitto di attentato a impianti di pubblica utilità sussiste anche in relazione alle condotte dirette a danneggiare o distruggere sistemi informatici o telematici di pubblica utilità, ovvero dati, informazioni o programmi in essi contenuti o a essi pertinenti (art. 420, 2° comma); la distruzione o il danneggiamento del sistema, dei dati, delle informazioni o dei programmi e l'interruzione anche parziale del sistema sono puniti con la reclusione da tre a otto anni (art. 420, 3° comma). È stato introdotto il delitto di frode informatica: il soggetto che, alterando in qualsiasi modo il funzionamento di un sistema informatico o telematico, ovvero intervenendo senza diritto con qualsiasi modalità su dati, informazioni o programmi in esso contenuti o allo stesso pertinenti, procura a sé o ad altri un ingiusto profitto, è punito con la reclusione da sei mesi a tre anni e con la multa da lire 100.000 a due milioni (art. 640 ter); il reato è aggravato se il fatto è commesso a danno dello Stato o di un altro ente pubblico ovvero con abuso della qualità di operatore del sistema (in tal caso la pena è la reclusione da uno a cinque anni e la multa da lire 600.000 a tre milioni); il reato è perseguibile a querela della persona offesa, salvo che ricorra l'ipotesi aggravata o un'altra aggravante. Costituiscono inoltre reato: l'accesso abusivo a un sistema informatico o telematico (art. 615 ter); l'intercettazione, l'impedimento o l'interruzione illecita di comunicazioni informatiche o telematiche (art. 617 quinquies); la falsificazione, alterazione o soppressione del contenuto di comunicazioni informatiche o telematiche (art. 617 sexies); il danneggiamento di sistemi informatici o telematici (art. 635 bis). Per quanto riguarda le norme di procedura, è consentita l'intercettazione del flusso di comunicazioni relativo a sistemi informatici o telematici ovvero intercorrenti tra più sistemi, nei procedimenti aventi a oggetto i reati indicati nell'art. 266 c.p.p. ovvero commessi mediante l'impiego di tecnologie informatiche o telematiche (art. 266 bis). In particolare, la dottrina ha messo in luce la nuova formula giuridica di violazione di un 'domicilio informatico' della persona.
Ai fini della lotta alla criminalità, facendo ricorso ai nuovi metodi di rilevazione elettronica e di comunicazione telematica, sono stati conclusi accordi sul piano internazionale, come l'accordo di Schengen del 14 giugno 1985 (cui l'Italia aderì il 27 nov. 1990), che regolamenta la collaborazione tra le forze di polizia di diversi paesi.
La telematica
Nel 1978 era stato pubblicato un rapporto su L'informatisation de la société, redatto da S. Nora e A. Minc per il presidente della Repubblica francese: in esso fece la sua apparizione il termine telematica, per indicare il metodo di trasmissione a distanza dei dati informatizzati, che già veniva diffondendosi e costituiva una nuova dimensione dell'informatica. In quella sede veniva tracciato il progetto di una rete di telecomunicazioni per la società francese, da cui è poi derivata la definizione di società dell'informazione (s'intende automatizzata) per la società tecnologica contemporanea.
Le prospettive aperte dalla telematica, ormai considerata come un'integrazione dell'i., hanno così generato un nuovo mezzo di comunicazione di massa della nostra epoca: dopo quelli della radio, del telefono e della televisione, si è creato un nuovo circuito informativo su scala planetaria. La rete di trasmissione per mezzo di cavi a fibre ottiche consente anzi di unificare i vari mezzi finora usati separatamente: un apparecchio, il telecomputer (o 'teleputer') funziona da telefono, telefax, radiotelevisore, computer ricevente e trasmittente. Il collegamento tra le varie reti ha consentito la creazione della rete mondiale, o World Wide Web, ovvero Internet, ideata da V. Cerf.
Con la diffusione su scala planetaria della possibilità di raccogliere e comunicare informazioni per iniziativa individuale di ogni utente, si è affermata la nuova forma della libertà informatica intesa come diritto di partecipazione al circuito informativo, e sono sorti nuovi problemi giuridici. Principale fra essi è quello di stabilire dei limiti alla capacità di veicolare messaggi che possono avere un contenuto illecito o eversivo; e anche quello di regolamentare l'impiego dei mezzi telematici a fini di propaganda e vendita commerciale e di riproduzione di programmi trasmessi. Questi problemi e altri connessi non hanno ancora avuto soluzioni legislative sul piano nazionale e internazionale tali da consentire un'adeguata sistemazione dottrinaria.
I contratti informatici
Un argomento di particolare rilievo nell'ambito dell'i. giuridica è quello che si riferisce ai contratti informatici, cioè stipulati avendo per oggetto la cessione o la locazione di sistemi informatici (contratti a oggetto informatico), ovvero utilizzando strumenti di comunicazione telematici, come, per es., la posta elettronica (E-mail) e il trasferimento elettronico di fondi.
La creazione del bene informatico per mezzo degli elaboratori elettronici ha dato origine a una varietà di nuovi tipi di negozi giuridici per coprire il largo prisma apertosi nei rapporti economici, e alla richiesta di nuove formule giuridiche e di garanzie per il riconoscimento legale degli accordi. Si possono individuare infatti cinque principali profili di contratto a oggetto informatico: di vendita, di locazione, di licenza d'uso del software, di manutenzione e di fornitura dei servizi e di assistenza ai programmi. Una nuova figura giuridica, sorta in connessione all'acquisto o al noleggio dell'elaboratore, è quella di leasing, poi estesa anche ad altri settori. È necessario, inoltre, tener presente la diversità dei contratti conclusi fra privati dai contratti conclusi fra privati e pubblica amministrazione; per questi ultimi è previsto in Italia un apposito 'Capitolato di oneri per gli acquisti e la locazione di apparecchiature e per la prestazione di servizi in materia di informatica'.
I contratti informatici propriamente detti sono quelli conclusi o eseguiti mediante strumenti informatici: come i contratti di borsa, quelli conclusi mediante EDI (Electronic Data Interchange), le operazioni bancarie elettroniche. Si sono posti perciò i problemi della sostituzione della forma elettronica alla forma scritta prima richiesta, della firma elettronica, della responsabilità contrattuale ed extracontrattuale nel nuovo contesto dell'elaborazione informatica, che hanno dato luogo ai contributi di dottrina e di giurisprudenza.
L'evoluzione dell'informazione giuridica
Le leggi in precedenza ricordate - sulla tutela dei programmi informatici, sulla repressione dei reati informatici, sulla protezione dei dati personali, sull'informatizzazione della pubblica amministrazione - indicano come il diritto dell'i., in diverse specificazioni (commerciale, civile, penale e amministrativo), sia entrato a far parte stabile e integrante del sistema giuridico italiano, in corrispondenza alla normativa di un diritto comune europeo.
Nel corso degli ultimi decenni del Novecento si sono intanto verificati ulteriori progressi nel campo dell'i. giuridica, considerata come una metodologia di applicazioni degli elaboratori elettronici al diritto. Sono avanzati gli studi e gli esperimenti sui 'sistemi esperti' giuridici, ossia su programmi di ricerca e di aggregazione dei dati, capaci di modificarsi e autocorreggersi con l'accrescimento e l'aggiornamento dei dati (input) per fornire soluzioni ai nuovi quesiti proposti (output). Si è verificata l'apparizione e la diffusione (prima negli Stati Uniti e poi in altri paesi di civiltà tecnologica) del telelavoro, il lavoro compiuto a distanza dal centro organizzativo e decisionale grazie all'uso dei computer e dei collegamenti telematici; il lavoro diventa personalizzato, l'orario di lavoro flessibile, viene risparmiato il tempo impiegato nei trasferimenti fra casa e ufficio: il rapporto di lavoro subisce una rilevante trasformazione (v. lavoro: Mutamenti sociali e nuovi lavori, in questa Appendice).
Un campo che si rivela ancora aperto alle attese, nel quale l'uomo contemporaneo va inoltrandosi, è quello delle applicazioni della comunicazione a distanza nei rapporti politici: il ricorso ai sistemi automatizzati di votazione invece dei cartacei (già operanti nei calcoli dei risultati elettorali); il ricorso a sondaggi e a referendum mediante le telecomunicazioni; il colloquio diretto per mezzo dei sistemi di trasmissione elettronica fra il cittadino e il rappresentante politico (quest'ultimo ritrovato tecnologico, alimentando il circuito informativo, potrebbe segnare forse l'avvento di una nuova forma di democrazia diretta).
bibliografia
V. Knapp, Moznosti pouziti kybernetickych metod v pravu, Praha 1963 (trad. it. L'applicabilità della cibernetica al diritto, Torino 1978).
V. Frosini, Cibernetica, diritto e società, Milano 1968, 1983⁵, poi in V. Frosini, Informatica, diritto e società, Milano 1988, 1992².
M.G. Losano, Giuscibernetica, Torino 1969.
A. Predieri, Gli elaboratori elettronici nell'amministrazione dello Stato, Bologna 1971.
S. Rodotà, Elaboratori elettronici e controllo sociale, Bologna 1973.
A. Baldassarre, Privacy e costituzione. L'esperienza statunitense, Roma 1974.
A. Gallizia, E. Maretti, F. Mollame, Per una classificazione automatica di testi giuridici, Milano 1974.
G. Caridi, L'automazione amministrativa, Roma 1978.
S. Nora, A. Minc, L'informatisation de la société, Paris 1978 (trad. it. Convivere con il calcolatore, Milano 1979).
Camera dei deputati, Banche dati e tutela della persona, a cura di R. Pagano, con introd. di V. Frosini, Roma 1981.
Privacy e banche dei dati. Aspetti giuridici e sociali, a cura di N. Matteucci, Bologna 1981.
D.A. Limone, Informatica, diritto e pubblica amministrazione, Roma 1983.
Banche dati, telematica e diritti della persona, a cura di G. Alpa, M. Bessone, Padova 1984.
D.A. Limone, Politica e normativa comunitaria per l'informatica: 1974-1984, Milano 1985.
M.G. Losano, Corso di informatica giuridica, 2 voll., Torino 1985-86 (1° vol., Informatica per le scienze sociali; 2° vol., i, Il diritto privato dell'informatica; 2° vol., ii, Il diritto pubblico dell'informatica).
G. Caridi, Metodologia e tecniche dell'informatica giuridica, Milano 1987.
I contratti di informatica, a cura di G. Alpa, V. Zeno-Zencovich, Milano 1987.
I. D'Elia Ciampi, C. Ciampi, L'informatica nella pubblica amministrazione, Roma 1987.
R. Borruso, Computer e diritto, Milano 1988.
R. Pagano, Informatica e diritto, Milano 1988.
G. Corasaniti, Diritto e tecnologie dell'informazione, Milano 1990.
G. Taddei Elmi, Dimensioni dell'informatica giuridica, Napoli 1990.
V. Frosini, Contributi a un diritto dell'informazione, Napoli 1991.
U. Fantigrossi, Automazione e pubblica amministrazione, Bologna 1994.
E. Giannantonio, Manuale di diritto dell'informatica, Padova 1994.
S. Rodotà, Tecnologie e diritti, Bologna 1995.
G. Finocchiaro, I contratti informatici, Padova 1997.